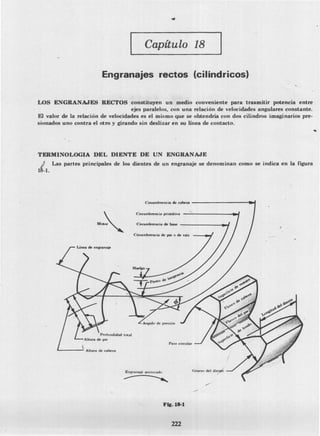
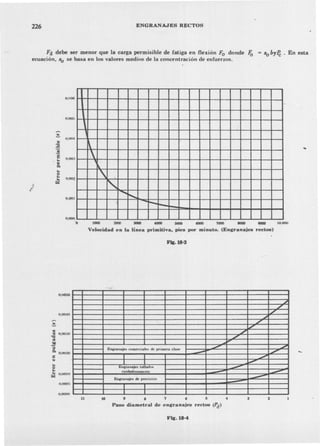
Este documento trata sobre engranajes rectos y cubre temas como: 1) La definición y propósito de los engranajes rectos para transmitir potencia entre ejes paralelos a una velocidad constante. 2) La terminología básica de los dientes de engranaje como diámetro, paso, profundidad y ángulo. 3) Las ecuaciones para calcular la carga, resistencia y esfuerzos en los dientes así como factores que afectan el diseño como materiales y velocidad.

1. Capítulo 18
Engranajes rectos (cilíndricos)
LOS ENGRANAJES RECTOS constituyen un medio conveniente para trasmitir potencia entre
ejes paralelos, con una relación de velocidades angulares constante.
El valor de la relación de velocidades es el mismo que se obtendría con dos cilindros imaginarios pre-
sionados uno contra el otro y girando sin deslizar en su línea de contacto.
...
TERMINOLOGIA DEL DIENTE DE UN ENGRANA.JE
l Las partes principales de los dientes de un engranaje se denominan como se indica en la figura
l§-l.
Cittunf_neía de eobeza ----------1.,.
1.- -' Altura de cabeza
Circunrerencla pnmíti," - - - - - - - -.....,
Ciuunfrrrncia de base ......,
CiraaorrrelK'ia de- pie ;) «k ralz
FIc.18-1
222

2. DEFINICIONES
ENGRANAJES RECTOS 223
Paso circular Pe es la distancia desde un punto de un diente hasta el punto correspondiente
de un diente adyacente, medida sobre la circunferencia primitiva.
Pe n O/N
donde D = diámetro primitivo en pulgadas y N = número de dientes del engranaje.
Paso diametral Pd es el número de dientes de un engranaje por pulgada de diáme~o.
Pe! N/O Obsirvese que Pe x Pd = 71.
Línea de engranaje es una linea normal al perfil de un par de dientes engranados, en su punto
de contacto. .
Angulo de presión rp es el ángulo entre la línea de engranaje y la tangente común a las cir-
cunferencias primitivas.
Punto de tangencia es el punto de tangencia de las circunferencias primitivas.
Razón de las velocidades angulares (o razón de trasmisión) es la razón de la velocidad
angular del piñón a la velocidad angular del engranaje acopla~. La razón de las velocidades angula-
lares es inversamente proporcional a la razón de los númer't'de dientes de los dos engranajes y para
el caso de engranajes rectos es también proporcional a la razón de los diámetros primitivos.
Razón de las velocidades angulares = NgINp = DgIDfJ
LEY FUNDAMENTAL DEL ENGRANArJE. La normal común al perfil del diente en el punto
. de contacto debe pasar siempre por un punto fijo,
llamado punto de tangencia, con el fin de mantener constante la razón de las velocidades angulares
de 10$ dos engranajes. La curva evolvente satisface la ley del engranaje y es la que se usa más a me-
nudo en el perfil de los dientes de engranajes. Frecuentemente se utiliza en el perfil de los dientes de
un engranaje, una combinación de las curvas evolvente y cicloide, para evitar interferencia. En esta
forma compuesta, aproximadamente el tercio central del perfil tiene forma evolvente, mientras
que el resto es cicloidal.
INTERFERENCIA. Con ciertas condiciones, los perfiles de forma evolvente recubren o cortan los
perfiles de los dientes del otro engranaje. Esta interferencia se puede: vitar si
el radio d. cabeza máximo de cada engranaje es igual o menor que
V(radio de la circunferencia de base)2 + (distancia entre centros)2 (sen rp )2
PROPORCIONES DE LOS DIENTES DE ENGRANAJES NORMALIZADOS
¡ IdO IdO 20
0
• 200
.r
Compuesto Evolvente y prof. tot. Evolventey prof. tol. Evolvente "5tub"
""
Altura de cabeza
I I I 0,8
- _.
Id Id Id Id
1,157 ],157 1,]57 IAltura de pie mínima
~ p¡- ~ Pd
2,i57 2.,]57 2,157 1,8
Profundidad total
p;- --r ~ Id
Huelgo
0,]57 0,157 0,]57 0,2
T" T" Id Id
1

3. 224 ENGRANAJES RECTOS
PASOS NORMALIZADOS. Los pasos diametrales normalizados que se utilizan comúnmente son:
1 a 2, de 1/4 en 1/4; 2 a 4. de 1/2 en 1/2; 4 a 10, de 1 en 1; 10 a 20,
de 2 en 2 y 20 a 40, de 4 en 4.
OBJETIVOS DEL DISEÑO. El diseño del diente de un engranaje consiste principalmente en deter-
minar el paso y la longitud del diente necesarios para obtener la
resistencia, la durabilidad y la economía de fabricación adecuadas.
RESISTENCIA DE LOS DIENTES DE UN E~­
GRA~AJE - Ecuación de Lewis. Al comenzar la
acción entre un
par de dientes que engranan, el flanco del diente motor
hace contacto con la punta del diente accionado. Des-
preciando el rozamiento, la carga total Wn es normal
al perfil del diente y se supone que es condU(~idapor este
diente. W, la carga componente de Wn perpendicul:tr a
la línea media del diente, produce un esh.lc'rzo de flexión
en la base del diente. La componente radial W,.. se
desprecia. La parábola que se muestra en la figura 18-2
bosqueja una viga de resistencia constante. Por tanto,
la sección más débil del diente es la sección A-A, donde
la parábola es tangente al contorno del di~nte. Se su-
pone que la carga está uniformemente distribuida a
través de toda la cara del diente.
El esfuerzo de flexión producido, s, es
Fq.18-2
J/e
s = T 6J!
bt2
y IV = sb(t2
/6h> = sb(t2
/6hPr;>Pe
donde c =-t/2. 1= btS /12 y M = Wh.
La relación t2
/6hPc es una cantidad adimensional denominada el factor de forma y, cuyos va·
lores están tabulados en la tabla I. Este factor de forma y es una función de la forma del diente, la cua'
a su vez depende del sistema de dientes utilizado y del número de dientes del engranaje.
Por conveniencia W se aproxima a la fuerza trasmitida F, la cual se define corno el momentc
de torsión dividido por el radio primitivo. Por consiguiente, remplazando F por W y y por t2/6hPc
obtenemos la forma usual de la ecuación de Lewis:
F sbPe;y
Para condiciones de diseño ordinarias, la longitud del diente, b, se limita a un máximo de
veces el paso circular. Haciendo b = kPc , donde k ~ 4,
F = sP/kr :" s7T2krlI{
En el diseño de un engranaje, basado en la resistencia, puede conocerse o no el diámetro prim
tivo. Si el diámetro primitivo es conocido, se puede utilizar la siguiente forma de la ecuación de Lewi
2
Id Ir = Sk7T2
/ F
donde s = esfuerzo permisible; k = 4, límite superior; F = fuerza trasmitida = 2Mt /D. Luego
expresión anterior da un vaJo~ numérico permisible de la relación ~'1r, que controla el diseñ
puesto que se basa en un esfuerzo permisible.
Si se desconoce el diámetro primitivo, se puede utilizar la siguiente forma de la ecuación de Lew
donde s
s = 2M/flk7T2rN
esfuerzo ~ esfuerzo permisible; M t = momento de torsión en el engranaje menos res

4. ENGRANA.JES RECTOS 225
tente; k = 4, límite superior; .v = número de dientes del engranaje menos resistente. Esta expresión
, nos da un valor del esfuerzo producido, en funcicln del paso diametral. El número mínimo de dientes,
N, -generalmente está limitado a 15_
En los dos casos anteriores, el máximo paso diametral posible proporcionará el diseñu más eco-
nómico.En general, cuando se conocen los diámetros, se diseña por el mayor número de dientes posible;
cuando no se conocen los diámetros, se diseña con los menores pasos diametrales posibles.
ESFUERZOS PERMISIBLES EN EL DIE='l'TE. Los esfuerzos máximos permisibles en el diseño
de dientes de engranajes, dependen del material
seleccionado y de la velocidad de la línea primitiva. Para engranajes rectos, .-
s permisible = s ( 600 )
o 600+ V
( 1200 )
-'b 1200 + V
para V menor que 2000 pies/min
para V entre 2000 y 4000 pies/min
para V mayor que 4000 pies/min
So (78 :8,11')
donde So es el coeficiente estático unitario corregido por los valores de la concentraciún media de
esfuerzos del material del engranaje (psi) y V es la velocidad en la Línea primitiva (pies/min).
VALORES DE so' Los valores de So de diferentes materiales para engranajes están catalogados en
." . las publicaciones de la American Gear Manufacturen, Association, en diferentes
manuales de ingenieria yen la mayoría de los textos de diseño. Los valores de ~ para hierro y bronce
fundidos son 8000 psi y 12.000 psi, respectivamente. Para aceros al carbono So está comprendido entre
10.000 psi y 50.000 psi, depe~diendodel co.ntenido de carbono y del tratamiento térmico. En general, se
puede tomar So como una tercera parte de la resistencia al fallar del material, aproximadamente.
DISEÑO BASADO EN EL ENGRANAJE MAS DEBIL. La cantidad de fuerza que puede tras-
mitirse al diente de un engranaje es
una función del producto soy, como se expresa en la ecuación de Lewis. Para dos engranajes acoplados,
el más débil tendrá el menor valor de soy. !
Cuando los dos engranajes están hechos del mismo material, el más pequeño (piñón) será el más
débil Y por tanto, controlará el diseño.
CARGAS DINAMICAS EN EL DIENTE - Ecuación de Buckingham. Las inexactitudes en el
perfil del diente y en
los espaciamientos, el desalineamiento en el montaje y la deformación del diente J>roducida por la carga
causan cambios de velocidad que producen fuerzas dinámicas en los dientes, que son mayores que la
fuerza trasmitida. La carga dinámica Fd' aproximada por un análisis dinámico más detallado,
para condiciones medias de masa, es la propuesta por Buckingham.
0,05 V(bC + F) + F
0,05 V + .jbC + F
donde Fd
V
b
F
C
carga dinámica, en lb
velocidad en la linea primitiva, pies/min
longitud del diente, en pul
momento de torsión del engranaje
radio primitivo del engranaje
una constante que depende de la forma del diente, del material 'utilizado y del
grado de exactitud con que se talle el diente. En la tabla Il se han tabulado algunos
valores de C. Las curvas que indican la relación de los errores en los perfiles de
los dientes con la velocidad en la linea primitiva y con el paso diametral. se mues-
tran en las figuras 18-3 y 18-4.

5. 226 ENGRANAJES RECTOS
Fa debe ser menor que la carga permisible de fatiga en flexión Fo donde Fo = So brPe ' En esta
ecuación, So se basa en los valores medios de la concentración de esfuerzos,
0.001
..
~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Velocidad en la línea primitiva. pies por minuto. (Engranajes reetos)
.
~
,
".
"""""'".......
,
-¡--.""-
,
0.002
0.003
0.000
o
11.005
,...
~
~
:ti
..'S..CI
a.
..olo
..~
¡!
Ffc.18-3
0.0000
0.0040
..~ O.ll(J:;l(l
"CI
<lJ
~
='
a. 0.0020
1:
~
..o..~ 0.1..010
0.0000
"
~
./
./
~
./
1/
"'. /
""'"Enpanajel; ~"'_rcia"'" de primera d .....
.JI" ~
- ~
I .JI!"
I I ".,
Enrranajes tallad.,. .--
euidad058menk
- ..--
Enpanajes .. pt'l'ci.íÓn
.--
I I
I I
11 10 9 8 7 6 5 4
Paso diametral de engranajes rectos (Pa)
3 2
Ftc·18-4

6. TABLA 1 • Factor de for ma y • para utilizar en la ecuación de resistencia de Lewis.
Número de
dientes
Forma evolvente o compuesta Forma evolvente a 20n
y Forma evolvente
a l4~" Y profu ndidad total profu ndidad total "stub" a 20°
12
13
14 : J>
15
16
17
18
19
20
21
23
25
27
30
34
38
43
50
60
75
100
150
300
Cremallera
0,067
0,071
0,075
0,078
0,081
0,084
0,086
0,088
0.090
0,092
0,094
0,097
0,099
0,101
0,104
0,106
0,108
0,110
0,113
0,115
0,117
0,119
I
0,122
0,124
0,078
0,083
0,088
0,092
0,094
0,096
0,098
0,100
0,102
0,104
0,106
0,108
0,111
0,11"4 -
0,118
0,122
0,126
0, 130~
0,134
0,138
0,142
0,146
0,150
0,154
0,099
0,103
0,108
0,111
0,115
,0,117
0,120 '"
0,123
0,125
0,127
0,130
0,133
0,136
0,139
0,142
0,145
0,147
0,151
0,154
0,158
0,161
0,165
0,170
0,175

7. 1
228 ENGRANAdES RECTOS
TABLA 11 - Valores del factor de deformación e - para verificar cargas dinámicas.
Materiales Diente Error del diente - pulgadas
de forma
Piñón Engranaje evolvcnte 0,0005 0,001 0,002 0,003
hierro fundido hierro fundido Id° 400 800 1600 2400
acero hierro fundido Ido 550 1100 2200 3300
aeero acero 14!O 800 1600 3200 4'800
hierro fundido hierro fundido 2(JC y pwfun- 415 830 1660 2490
d ¡dad tlital
acero hierro fundido 20~ y TJrufun- 570 1140 2280 3420
didad lOtaI
acero acero 20" y profun- 830 1660 3320 4980
didad 1utaI
hierro fundido hierro fundido 20' "srub" 430 860 1720 2580
acero hierro fundido 20 U:,tub~'t
590 1180 2360 3540
acero acero 20" "stub" 860 1720 3440 5160
TABLA III
Los 'alores de Ses utilizados en la ecuación de carga de desgaste dependen de la combinación
de los materiales del engranaje y del piñón. Aquí se tabulan los valores de ses y K par~algun()s ma-
teriales.
Número de dureza Brinell Límite Factor del esfuerzo de-rat,iga
promedio del piñón de acero
de fáliga K ..
superficial
y el engranaje de acero ses 14!0 20°
- ".
150 50.000 30 41
200 70.000 58 79
250 90.000 96 131
300 110.000 144 196
400 150.000 268 366
Número de dureza Brine)), BHN
Piñón de acero Engranaje
150 Hierro fundido 50.000 44 60
200 Hierro fundido 70.000 87 119 .
250 Hierro fundido 90.000 144 196
150 Bronce fosforado 50.000 46 62
200 Bronce fos forado 65.000 73 100
Piñón de hierro Engranaje de hierro
fundido fundido 80.000 152 208
Piñón de hierro Engranaje de hierro
fundido fundido 90.000 193 284