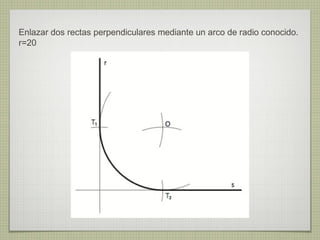
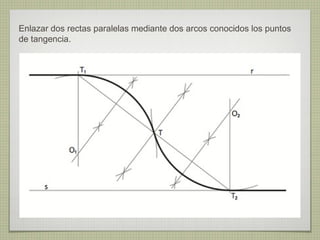
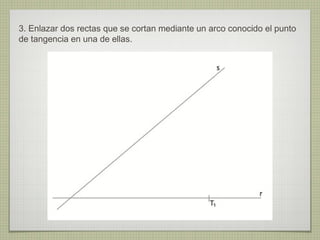
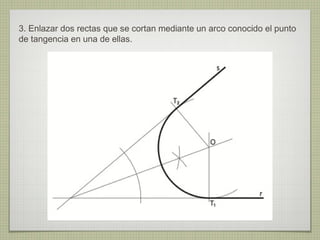
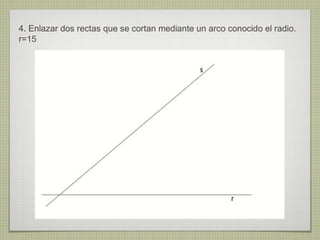
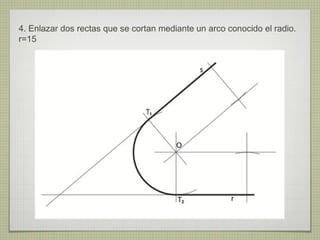
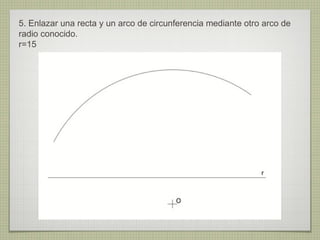
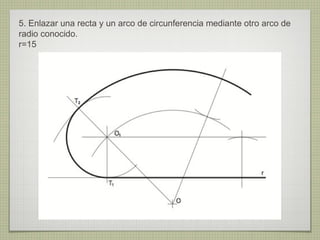
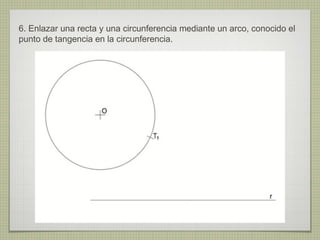
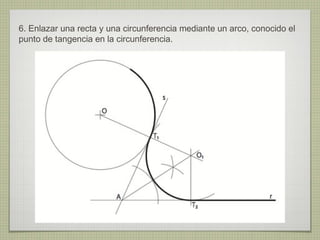
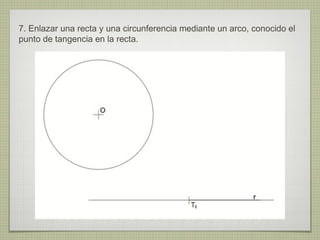
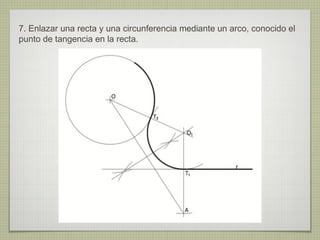
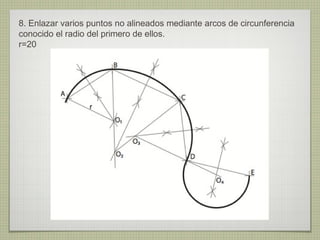
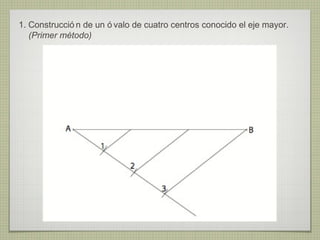
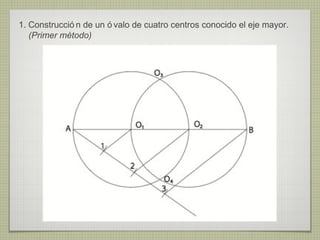
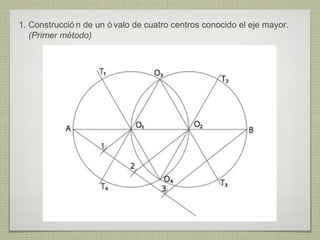
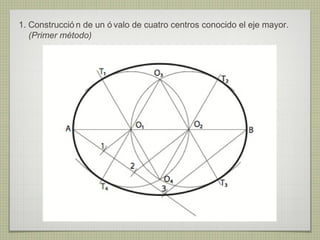
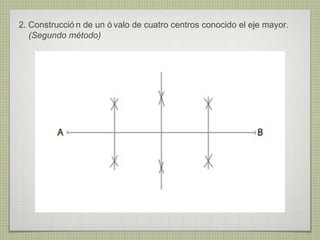
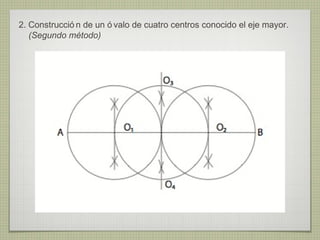
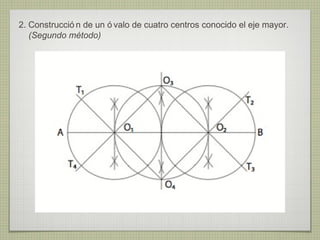
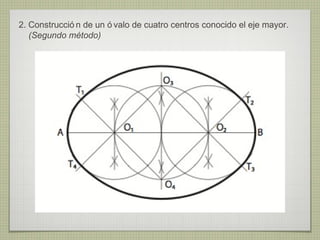
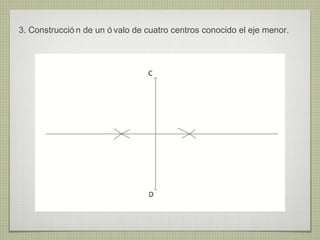
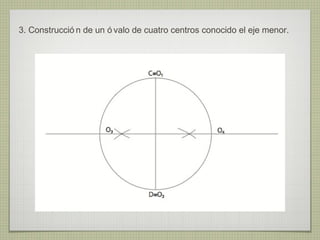
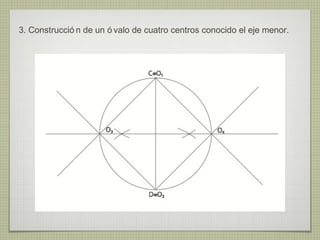
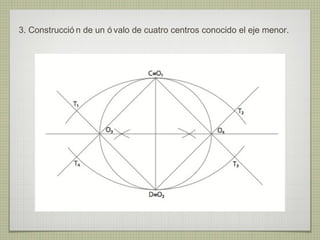
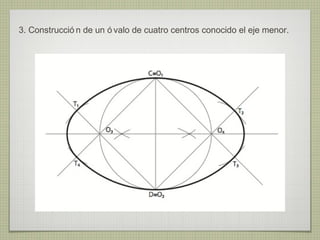
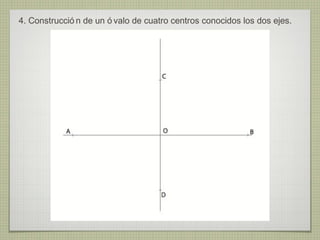
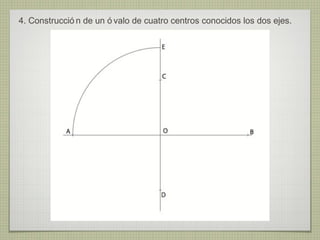
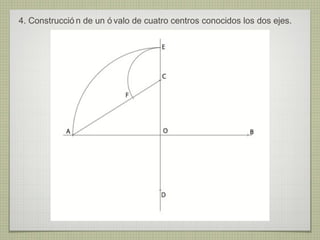
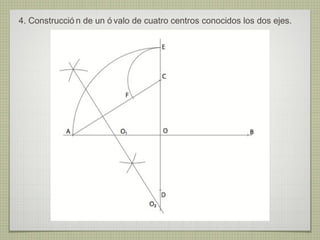
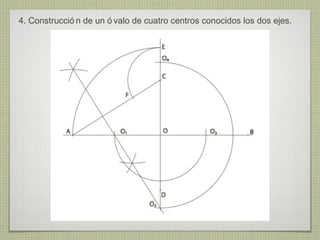
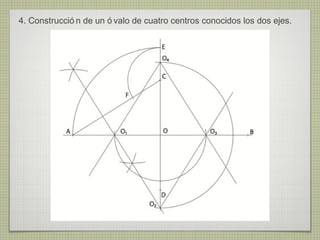
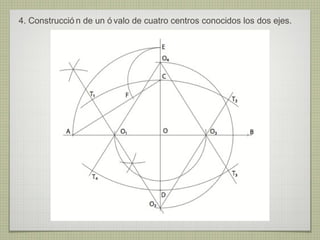
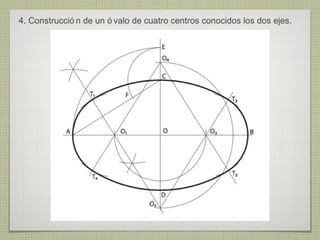
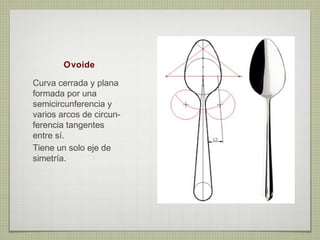
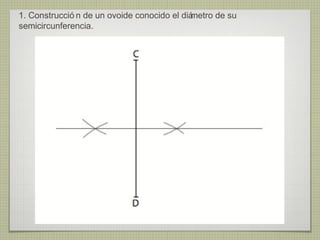
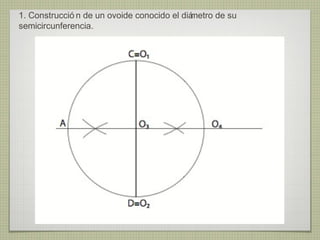
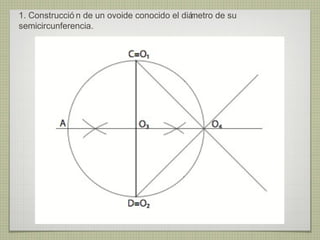
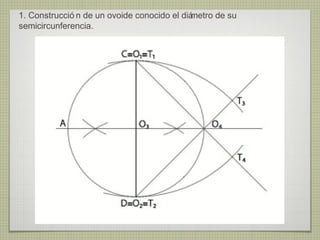
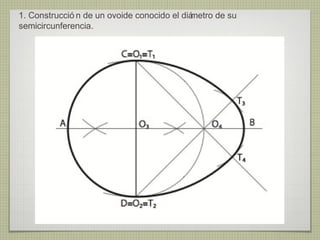
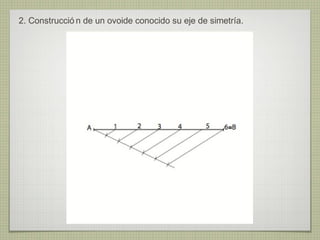
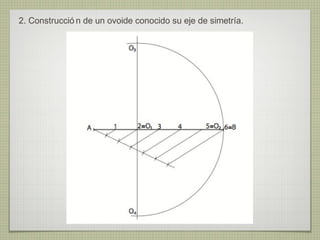
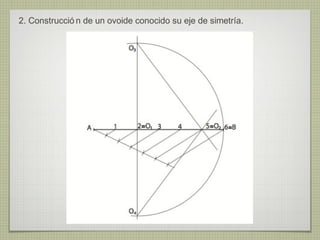
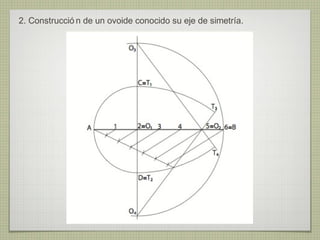
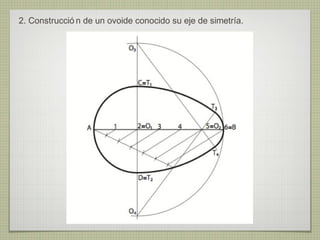
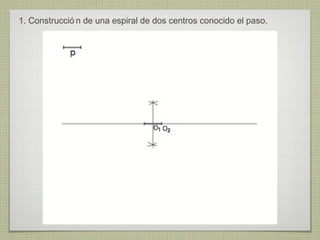
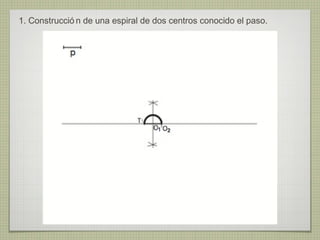
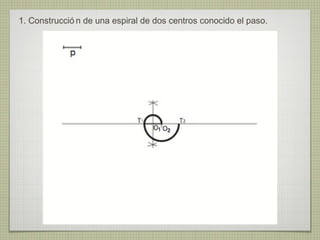
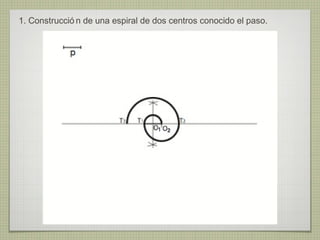
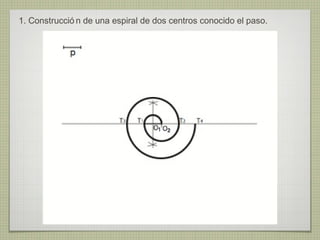
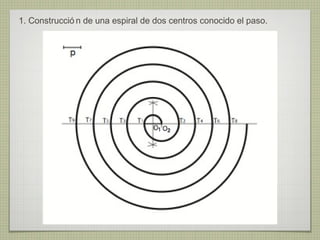
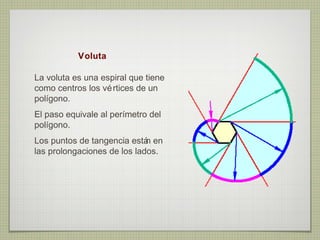
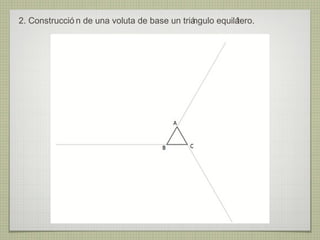
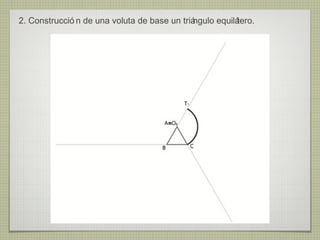
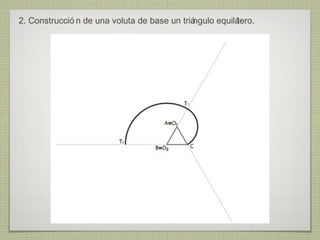
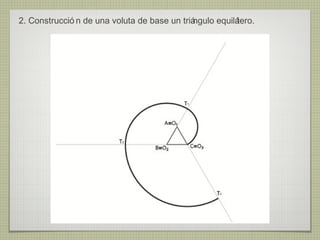
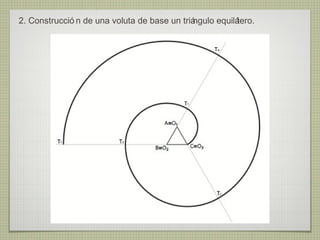
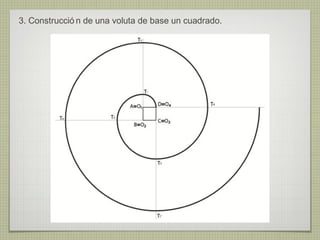
El documento describe diferentes técnicas de enlaces y curvas utilizadas en dibujo técnico. Explica cómo unir dos líneas mediante enlaces tangentes y presenta varios ejemplos de enlaces de rectas y curvas. También define curvas técnicas como el óvalo, el ovoide y la espiral, y proporciona instrucciones para construir diferentes versiones de cada una.

1. ENLACES Y CURVAS
TÉCNICAS
Dibujo Té cnico 1º Bachillerato

2. Enlaces
Un enlace es la unió n de dos líneas,
curvas o rectas, de modo que parezca
una sola línea continua.
Los enlaces son aplicaciones
concretas de las tangencias. Para
realizar un enlace se procede de la
siguiente forma:
1.Se resuelve el problema de
tangencias
2.Se deteminan con precisió n los
puntos de tangencia, que será los
n
puntos de enlace
3.Se traza la línea de enlace de forma
continua y uniforme

3. 1. Enlazar dos rectas perpendiculares mediante un arco de radio
conocido.
r=20

4. Enlazar dos rectas perpendiculares mediante un arco de radio conocido.
r=20

5. 2. Enlazar dos rectas paralelas mediante dos arcos conocidos los puntos
de tangencia.

6. Enlazar dos rectas paralelas mediante dos arcos conocidos los puntos
de tangencia.

7. 3. Enlazar dos rectas que se cortan mediante un arco conocido el punto
de tangencia en una de ellas.

8. 3. Enlazar dos rectas que se cortan mediante un arco conocido el punto
de tangencia en una de ellas.

9. 4. Enlazar dos rectas que se cortan mediante un arco conocido el radio.
r=15

10. 4. Enlazar dos rectas que se cortan mediante un arco conocido el radio.
r=15

11. 5. Enlazar una recta y un arco de circunferencia mediante otro arco de
radio conocido.
r=15

12. 5. Enlazar una recta y un arco de circunferencia mediante otro arco de
radio conocido.
r=15

13. 6. Enlazar una recta y una circunferencia mediante un arco, conocido el
punto de tangencia en la circunferencia.

14. 6. Enlazar una recta y una circunferencia mediante un arco, conocido el
punto de tangencia en la circunferencia.

15. 7. Enlazar una recta y una circunferencia mediante un arco, conocido el
punto de tangencia en la recta.

16. 7. Enlazar una recta y una circunferencia mediante un arco, conocido el
punto de tangencia en la recta.

17. 8. Enlazar varios puntos no alineados mediante arcos de circunferencia
conocido el radio del primero de ellos.
r=20

18. 8. Enlazar varios puntos no alineados mediante arcos de circunferencia
conocido el radio del primero de ellos.
r=20

19. Curvas té cnicas
Son curvas formadas a partir de los enlaces de varios arcos de
circunferencia.
Se utilizan en numerosos trazados, por ejemplo en arquitectura, en
diseñ o industrial o en diseñ o grá
fico.
Estudiaremos:
1.el ó valo
2.el ovoide
3.la espiral

20. Óvalo
Curva cerrada y
plana formada por
4 o má arcos de
s
circunferencia
tangentes entre sí.
Tiene dos ejes de
simetría
perpendiculares.

21. 1. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Primer método)

22. 1. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Primer método)

23. 1. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Primer método)

24. 1. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Primer método)

25. 1. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Primer método)

26. 2. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Segundo método)

27. 2. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Segundo método)

28. 2. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Segundo método)

29. 2. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Segundo método)

30. 2. Construcció n de un ó valo de cuatro centros conocido el eje mayor.
(Segundo método)

31. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

32. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

33. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

34. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

35. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

36. 3. Construcció n de un ó valo de cuatro centros conocido el eje menor.

37. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

38. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

39. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

40. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

41. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

42. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

43. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

44. 4. Construcció n de un ó valo de cuatro centros conocidos los dos ejes.

45. Ovoide
Curva cerrada y plana
formada por una
semicircunferencia y
varios arcos de circun-
ferencia tangentes
entre sí.
Tiene un solo eje de
simetría.

46. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

47. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

48. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

49. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

50. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

51. 1. Construcció n de un ovoide conocido el diá
metro de su
semicircunferencia.

52. 2. Construcció n de un ovoide conocido su eje de simetría.

53. 2. Construcció n de un ovoide conocido su eje de simetría.

54. 2. Construcció n de un ovoide conocido su eje de simetría.

55. 2. Construcció n de un ovoide conocido su eje de simetría.

56. 2. Construcció n de un ovoide conocido su eje de simetría.

57. 2. Construcció n de un ovoide conocido su eje de simetría.

58. Espiral
Curva abierta y
plana generada por
un punto que se
desplaza alrededor
de otro alejá
ndose de
é l a cada vuelta.
Se denomina espira
a cada vuelta
completa de la
curva.
Paso es la distancia
entre dos espiras
consecutivas.

59. 1. Construcció n de una espiral de dos centros conocido el paso.

60. 1. Construcció n de una espiral de dos centros conocido el paso.

61. 1. Construcció n de una espiral de dos centros conocido el paso.

62. 1. Construcció n de una espiral de dos centros conocido el paso.

63. 1. Construcció n de una espiral de dos centros conocido el paso.

64. 1. Construcció n de una espiral de dos centros conocido el paso.

65. 1. Construcció n de una espiral de dos centros conocido el paso.

66. 1. Construcció n de una espiral de dos centros conocido el paso.

67. Voluta
La voluta es una espiral que tiene
como centros los vé rtices de un
polígono.
El paso equivale al perímetro del
polígono.
Los puntos de tangencia está en
n
las prolongaciones de los lados.

68. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

69. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

70. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

71. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

72. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

73. 2. Construcció n de una voluta de base un triá
ngulo equilá
tero.

74. 3. Construcció n de una voluta de base un cuadrado.

75. 3. Construcció n de una voluta de base un cuadrado.

76. F, Mohedano
Dibujo Técnico 1º Bach.
IES Los Manantiales (Torremolinos)
IES Los Manantiales (Torremolinos)
IES Los Manantiales (Torremolinos)