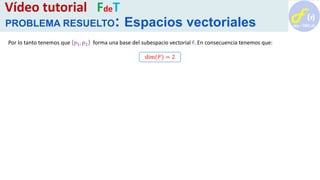
El tutorial aborda la teoría de espacios vectoriales, centrándose en cómo determinar si un conjunto de polinomios forma un subespacio vectorial y calcula su dimensión. Presenta un caso particular en el que se demuestra que el conjunto de polinomios cuya primera derivada se anula es efectivamente un subespacio vectorial de polinomios de grado menor o igual a 3. Además, se establece una base para este subespacio y se determina su complemento en el contexto del espacio vectorial dado.