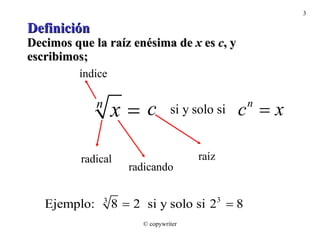
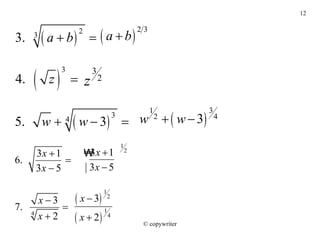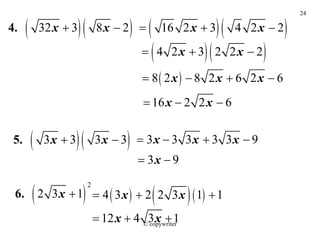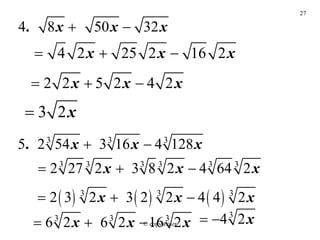El documento define conceptos sobre exponentes racionales y radicales. Explica cómo calcular raíces cuadradas, cúbicas y de mayor índice, así como simplificar, sumar, restar y multiplicar expresiones con radicales. También cubre cómo expresar raíces en forma exponencial y viceversa, y racionalizar numeradores y denominadores.

1. Exponentes Racionales y Radicales © copywriter

3. Definición Decimos que la raíz enésima de x es c , y escribimos; © copywriter

6. © copywriter

7. Propiedades de los radicales Sean m y n números naturales mayores que 1 . Si a y b son números reales tal que a > 0 y b > 0 ( números positivos ), entonces; © copywriter

8. Ejemplos: Simplifica. Suponga que las variables representan números positivos. © copywriter

9. Ejemplos: Simplifica. Suponga que las variables representan números positivos. © copywriter

10. © copywriter

11. Exponentes Racionales como Raíces Las raíces o radicales representan exponentes racionales. Ejemplos: © copywriter

12. © copywriter

13. Evalúa usando raíces: © copywriter

16. Ejemplos: Racionaliza cada denominador. Suponga que las variables representan números positivos. © copywriter

17. © copywriter

19. Ejemplos: Racionaliza el denominador. © copywriter

20. Ejemplos: Racionaliza el numerador. © copywriter

21. © copywriter

23. Ejemplos : Multiplica las expresiones con radicales. Suponga que las variables representan números positivos. © copywriter

24. © copywriter

26. Ejemplos: Suma y/o resta las expresiones con radicales. Suponga que las variables representan números positivos. © copywriter

27. © copywriter