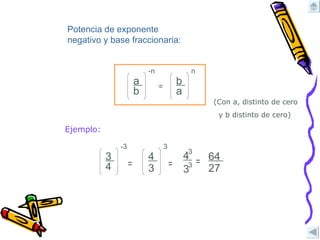
El documento define potencias, sus propiedades y notación científica. Explica que una potencia es la multiplicación reiterada de una base, con el exponente indicando la cantidad de multiplicaciones. Describe propiedades como la suma de exponentes al multiplicar potencias de igual base y la resta al dividir. Además, diferencia notación científica de potencias de base 10 y da ejemplos de su uso.

1. Potencias

2. Objetivos: Reconocer la definición de potencia de base racional y de exponente entero. Aplicar las propiedades de las potencias. Diferenciar notación científica de notación de potencia de base 10. Analizar problemas de crecimiento o decrecimiento Exponencial.

3. NÚMEROS CONJUNTOS NUMÉRICOS REGULARIDADES Y PATRONES POTENCIAS

4. Potenciación 1.1 Definición 1.2 Propiedades 1.3 Potencias de base 10 1.4 Signos de una potencia Potencias

5. 1.1 Definición Corresponde a una multiplicación reiterada de términos o números iguales. El término o número que se va multiplicando, se llama “base” y la cantidad de veces que se multiplica dicha base se llama “exponente”. 1. Potenciación a n = n veces Ejemplo: 7 3 = 7 ∙ 7 ∙ 7 = (-0,6) 2 = (-0,6) ∙ (-0,6)= 0,36 343 a ∙ a ∙ a ∙ a ∙ … a ∙ ∙ a

6. -3 2 = (-3) 2 ya que: -3 2 = - 3 ∙ 3 = -9 y (-3) 2 = (-3) · (-3) = 9 ya que: y = 2 3 3 2 3 3 = 2 3 3 = 2 ∙ 2 ∙ 2 3 8 3 2 3 3 = = 8 27 2 3 2 3 2 3 ∙ ∙

7. 1.2 Propiedades Multiplicación de Potencias De Igual Base: 2 3 ∙2 4 = Se conserva la base y se suman los exponentes. Ejemplo: 5 3+4 = 5 7 (2 ∙2 ∙2)(2 ∙2 ∙2 ∙2)= 2 7 =128 (0,3) ∙(0,3) 2 = (0,3) 3 a n+m a n ∙ a m = 5 3 ∙ 5 4 =

8. Se multiplican las bases, conservando el exponente. Ejemplo: 8 7 Multiplicación de Potencias De Igual Exponente: (a ∙ b) n a n ∙ b n = 8 5 ∙ 4 2 ∙ 2 2 = 8 5 ∙ (4 ∙ 2) 2 = 8 5 ∙ 8 2 =

9. División de Potencias De igual Base: Se conserva la base y se restan los exponentes. Ejemplo: = 9 17 9 23-6 a n-m a n : a m = 9 23 9 6 =

10. Se dividen las bases y se conserva el exponente. Ejemplo: 7 5 : (28:4) 2 = 7 3 División de Potencias De igual Exponente: (a : b) n a n : b n = 7 5 : 4 2 28 2 = 7 5 : 7 2 =

11. Potencia de Potencia: Se multiplican los exponentes. Ejemplo: (2 10 ) 4 = 2 10 ∙ 4 = 2 40 (a n ) m = a m ∙ n

12. Potencia de Exponente Negativo: Se invierte la base y se eleva al exponente positivo. Potencia de exponente negativo y base entera: (Con a, distinto de cero) Ejemplo: 1 a -n = a n 5 -2 ∙ 15 3 2 = ∙ (5) 2 5 2 1 = 25 1 ∙ 25 = 1

13. Potencia de exponente negativo y base fraccionaria: (Con a, distinto de cero y b distinto de cero) Ejemplo: 3 3 = 4 3 a b -n = b a n 3 4 -3 = 3 4 3 = 64 27

14. Potencias de exponente cero: a 0 = 1 (para todo a, distinto de cero) 0 0 : indefinido Ejemplo: = 1 7 3 - 40 7 – (15-8) 7 3 - 40 0 =

15. 1.4 Signos de una potencia Potencias con exponente par: Las potencias con exponente par, son siempre positivas. Ejemplo: (-11) ∙ (-11) = 121 (-11) ∙ (-11) = 2) -3 5 4 = 81 625 5 (-3) 4 4 = 1) (-11) 2 =

16. Potencias con exponente impar: En Las potencias con exponente impar, la potencia conserva el signo de la base. Ejemplo: (-12) ∙ (-12) ∙ (-12) = -1.728 1) (-12) 3 = 2) -2 3 -5 = 3 -2 5 = (3) 5 (-2) = 5 243 -32 = 243 32 -

17. 1.3 Potencias de base 10 Con exponente positivo: 10 1 = 10 10 2 = 100 10 3 = 1000 Ejemplo: 54.000.000 = 54 ∙ 1.000.000 = 54 ∙ 10 6 (Notación en base 10) 10 0 = 1

18. = 4 ∙ 10 -5 (notación en base 10) Con exponente negativo: Ejemplo: 0,1 0,01 0,001 0,00004 = 4 ∙ 0,00001 10 = 1 100 = 1 10 -3 = 1 1.000 = 10 -1 = 10 -2 = 4 100.000

19. Ejemplo: Determinar el número de bacterias que hay en una población, después de 38 horas, si se sabe que inicialmente había 10.000 bacterias, y que la población se triplica cada una hora. Solución: Por lo tanto, el número de bacterias después de 38 horas es: . Cantidad inicial = 10.000 Después de: 1 hora = 10.000·3 = 10.000·3 1 = 30.000 2 horas = 10.000·3·3 = 10.000·3 2 = 90.000 3 horas = 10.000·3·3·3 = 10.000·3 3 = 270.000... Después de x horas = 10.000 · 3 x . f(x)= 10.000 · 3 38

20. Desafío Si una cierta cantidad de bacterias se duplica cada media hora, y consideramos que un alimento está contaminado cuando la cantidad de bacterias es mayor que 160.000 por cm 3 . ¿Cuánto tiempo puede permanecer un alimento no contaminado si inicialmente tiene 10.000 bacterias por cm 3

21. Notación Científica La notación científica (o notación índice estándar ) es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar fácilmente números muy grandes o muy pequeños. Los números se escriben como un producto: a  10 n siendo: a un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente. n un número entero, que recibe el nombre de exponente

22. Ejemplo 1) 23.000 = 2,3  10 4 2) 456.000 = 4,56  10 5 3) 0,00087 = 8,7  10 -4 4) 0,00107 = 1,07  10 -3