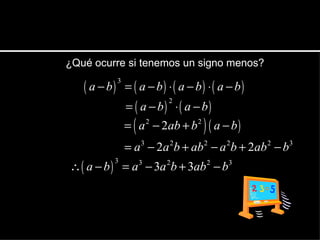
El documento explica diferentes productos notables de álgebra, incluyendo la fórmula general para el cuadrado de un binomio, la suma por su diferencia, y el cubo de un binomio. Proporciona ejemplos para ilustrar cómo aplicar estas fórmulas y resuelve productos algebraicos usando las reglas de los productos notables.

1. Profesor Practicante: Ignacio Espinoza Braz Comunidad “San Marcos” Subsector de Matemática Arica

2. Existen algunos productos algebraicos que responden a una regla cuya aplicación simplifica la obtención de resultados. Éstos productos reciben el nombre de Productos Notables. Algunos de ellos son: Cuadrado de Binomio Productos de Binomios que tienen un término común Suma por su Diferencia Cubo de Binomio

3. Para encontrar la formula general, haremos el producto de los binomios idénticos.

4. Veamos otro ejemplo: ¿Qué pasa si tenemos un signo menos?

5. En general podemos decir que: “El cuadrado de binomio es siempre igual al Cuadrado del primer Término (siempre positivo), más o menos, el doble del producto entre el primer término por el segundo, más el cuadrado del segundo término (siempre positivo)”

6. Cuando los términos se están sumando Cuando los términos se están restando

7. Para encontrar la formula general, haremos el producto de los binomios.

8. Veamos otro ejemplo:

9. Veamos otro ejemplo, muy distinto a los anteriores:

10. En general podemos decir que: Se eleva al cuadrado el primer término Se suman o restan los términos no comunes, multiplicado por el término común Se multiplican los términos no comunes

11. Para encontrar la formula general, haremos el producto de los binomios.

12. Veamos otro ejemplo:

13. En general podemos decir que: “La suma por su diferencia es igual cuadrado de los términos que tienen igual signo, menos el cuadrado de los términos que tienen distinto signo”

14. Para encontrar la formula general, resolveremos el cubo del binomio como un producto de factores iguales.

15. ¿Qué ocurre si tenemos un signo menos?

16. Cuadrado de Binomio Productos de Binomios que tienen un término común Suma por su Diferencia Cubo de Binomio

17. Ahora, trabajemos con la guía de ejercicios entregada