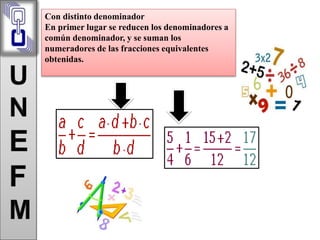
Este documento trata sobre las operaciones básicas de la adición, sustracción, multiplicación y división de números reales. Explica cómo se realizan estas operaciones con números enteros, decimales y fraccionarios, así como las propiedades asociadas a cada operación como la conmutativa, asociativa y distributiva.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD NACIONAL EXPERIMENTAL
“FRANCISCO DE MIRANDA”
ÁREA CIENCIAS DE LA EDUCACIÓN
PROGRAMA DE EDUCACION
MATEMÁTICA MENCIÓN INFORMÁTICA
Integrantes :
Auximar Brett
Areany Urbina
SANTA ANADE CORO, OCTUBRE 2014

2. Todos los números que usamos
en nuestra vida diaria son
números reales.
Es una operación básica ,
que se representa con el
signo (+), consiste en
combinar o añadir dos
números o más para
obtener una cantidad final
o total.
a + b = c
Ejemplo: 10+4=14

3. ADICIÓN DE NUMEROS DECIMALES
Para sumar números decimales debemos seguir el
mismo procedimiento que utilizamos para sumar
números naturales, sólo que debemos alinear las
comas de los sumandos y al resultado de la suma se
le coloca la coma en la misma ubicación.
4 8 ,136
+ 5,02
53 ,156

4. SUMA DE FRACCIONES CON IGUAL
DENOMINADOR
Se suman los numeradores y se mantiene
el denominador.

5. Con distinto denominador
En primer lugar se reducen los denominadores a
común denominador, y se suman los
numeradores de las fracciones equivalentes
obtenidas.

6. Propiedades de la adición
Conmutativa:
El orden de los sumandos no
varía la suma.
a + b = b + a
3 + 2 = 2 + 3
5 = 5
Asociativa:
El modo de agrupar los
sumandos no varía el
resultado.
(a + b) + c = a + (b + c)
(3 + 4) + 2 = 3 + (4 + 2)
7+ 2 = 3 + 6
9 = 9

7. Propiedad distributiva:
La suma de dos números multiplicados por un tercer
número es igual a la suma de cada sumando
multiplicado por el tercer número.
4 x ( 6 + 3) = 4 x 6 + 4 X 3
4 x 9 = 24 + 12
36 = 36
A x (b + c ) = a x b+ a x c

8. Elemento neutro:
El 0 es el elemento neutro de
la suma porque todo número
sumado con él da el mismo
número.
a + 0 = a
9 + 0 = 9
Elemento opuesto
Dos números son opuestos si
al sumarlos obtenemos como
resultado el cero.
a − a = 0
50 – 50 = 0

9. es la operación inversa a la
suma.
a - b = c Los términos que
intervienen en una
resta se llaman: a,
minuendo y b,
sustraendo. Al
resultado, c, lo
llamamos
diferencia.
 6 – 4 = 2
 560 -200= 360

10. Para restar números decimales debemos seguir el
mismo procedimiento que utilizamos para restar
números naturales, sólo que debemos alinear las
comas del minuendo y sustraendo y al resultado
colocarle la coma en la misma ubicación.
123 ,766
- 35,4
88,366 Con el mismo denominador:
se restan los numeradores y se
mantiene el denominador.

11. Con distinto denominador
En primer lugar se reducen los denominadores a
común denominador y se restan los numeradores
de las fracciones equivalentes obtenidas.

12. La multiplicación es una
operación matemática que
consiste en sumar un número
tantas veces como indica otro
número. Así, 4×3 (cuatro por
tres) es igual a sumar tres veces el
valor 4 por sí mismo (4+4+4).

14. PROPIEDAD CONMUTATIVA
El orden de los factores no altera
el producto 2x 3= 3x2
PROPIEDAD ASOCIATIVA
Cuando se multiplican tres o mas
números, podemos asociarlos o
agruparlos de diferentes maneras y
el resultado no varia
4x(5x6)= (4x5)x6
4x30 = 20x6
120 = 120

15. APLICACIÓN DE LAS PROPIEDADES
CONMUTATIVA Y ASOCIATIVA
Para multiplicar 4 x 19 x25=
Primero resolvemos (4 x 25)x 19=
Luego 100 x 19=
Resultado 1900
Para multiplicar 35 x 8 =
Descomponemos y asociamos 7 x ( 5 x 8 )=
Luego 7 x 40 =
Resultado 280

16. ELEMENTO NEUTRO
Cualquier número
multiplicado por 1 da como
resultado el mismo numero.
5 x 1= 5
1 x 123= 123
PROPIEDAD DE
ABSORCIÓN
Cualquier número
multiplicado por 0
da como resultado 0.
8 x 0 = 0
247 x 0 = 0
15 x 39 x 0= 0

17. PROPIEDAD DISTRIBUTIVA CON
RESPECTO A LA SUMA
Cuando tenemos que multiplicar un
número por la suma de otros dos
números, podemos distribuir o
repartir el factor para cada uno de
los sumandos.
4 x ( 3 + 8) = 4 x 3 + 4 X 8
4 x 11 = 12 + 32
44 = 44

18. APLICACIÓN DE LA PROPIEDAD
DISTRIBUTIVA CON RESPECTO A
LA SUMA.
 Para multiplicar 6 x 28 =
 Primero descompongo 6 x (20+ 8)=
 Luego aplico la propiedad distributiva 6 x 20 + 6 x 8=
Resuelvo 120 + 48=
Resultado 168

19. PROPIEDAD DISTRIBUTIVA CON
RESPECTO A LA RESTA.
Cuando tenemos que multiplicar un
número por la diferencia de otros dos
números, podemos distribuir o repartir
el factor para cada uno de los términos
de la resta.
5 x( 9- 3) = 5 x 9 – 5 x 3
5 x 6= 45 – 15
30 = 30

20. APLICACIÓN DE LA PROPIEDAD
DISTRIBUTIVA CON RESPETO A LA RESTA.
 Para multiplicar 6 x 47 =
Primero descompongo 6 x (50 – 3)
Luego aplico la propiedad distributiva 6 x 50 – 6 x 3
Resuelvo 300 - 18
Resultado 282

21. La palabra deriva del latín
Partir
separar
La división es una
operación de
descomposición que
consiste en averiguar
cuántas veces un
número (divisor) está
contenido en otro
número (dividendo).
El resultado de una
división recibe el
nombre de cociente.

23. En una división exacta el dividendo es igual al
divisor por el cociente. vamos a ver un ejemplo
dividiendo 15 entre 5.
D = d · c
En una división entera el dividendo es igual al
divisor por el cociente más el resto. . vamos a ver
un ejemplo dividiendo 17 entre 5.
D = d · c + r
15 = 5 · 3
17 = 5 · 3 + 2

24. Número decimal entre número entero
Se dividen como si fuesen enteros. En
la división al bajar el primer número
decimal, se escribe la coma en el cociente.
Vamos a ver un ejemplo, dividiendo 77,5
entre 25.

25. Número entero entre número decimal
Se quita la coma del divisor y se
añaden al dividendo tantos ceros
como decimales tiene el divisor.

26. Número decimal entre número decimal
Se quita la coma del divisor y se mueve la coma
del dividendo hacia la derecha, tantas
posiciones como decimales tenga el divisor.
Ahora vamos a dividir 278,1 entre 2,52.

27. Ahora vamos a ver cómo sacar decimales
Si al terminar la división nos ha quedado resto,
escribimos una coma en el cociente y añadimos
un cero en el dividendo. Si queremos seguir
sacando decimales, habrá que ir añadiendo
ceros en el dividendo. Vamos a ver un ejemplo
de sacar decimales, dividiendo 33 entre 6.

28. Veamos otra manera de realizar una
división