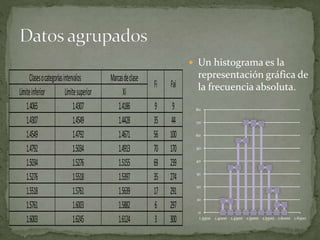
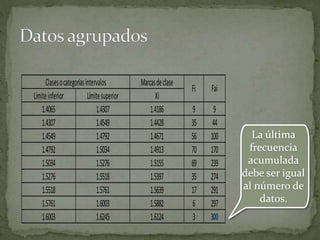
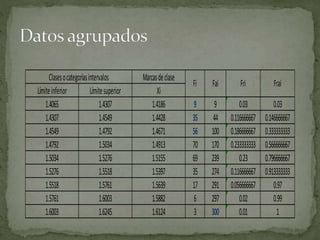
Este documento explica paso a paso cómo calcular las frecuencias a partir de datos agrupados en intervalos. Primero se calculan las marcas de clase para cada intervalo y luego las frecuencias absolutas contando los datos en cada intervalo. Luego se calculan las frecuencias acumuladas sumando las frecuencias absolutas. Finalmente se calculan las frecuencias relativas y relativas acumuladas dividiendo por el total de datos para expresar los resultados en porcentajes.

1. Castañeda Martínez Elías

2.  En esta presentación les mostraré paso a paso como sacar
las frecuencias.
 Primeramente vamos a calcular las marcas de clase (xi)
 Las marcas de clase representan, cada una de ellas, todos
los datos contenidos en el intervalo correspondiente.
 Se calculan promediando los límites inferior y superior de
los intervalos reales como se muestra en la diapositiva
siguiente.
 En el primer intervalo:
 1.4065+1.4307/2=1.4186

3.  Las marcas de clase representan,
cada una de ellas, todos los datos
contenidos en el intervalo
correspondiente.
 Al tomar la marca de clase para
efectuar todos nuestros cálculos
vamos a perder un poco de
exactitud.
 Es como si afirmáramos que
todos los datos en un intervalo
son iguales a la marca de clase.
Límiteinferior Límitesuperior
1.4065
1.4307
1.4549
1.4792
1.6245
Clasesocategoríasintervalos
1.5518
1.5761
1.6003
1.5034
1.5276
1.4307
1.4549
1.4792
1.5034
1.5276
1.5518
1.5639
1.5882
Marcasdeclase
1.5761
1.6003
Xi
1.4186
1.4428
1.4671
1.4913
1.5155
1.5397
1.6124

4.  Siguiente paso: Determinar las frecuencias absolutas
(fi)
 Esta parte del proceso es un tanto laboriosa cuando se
realiza a mano, ya que se debe contar para saber
cuántos datos están dentro de cada intervalo.
 Para el primer intervalo; ¿cuántos datos están entre
1.4065 y 1.4307? .

5. 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1.534 1.448 1.503 1.472 1.452 1.506 1.552 1.526 1.482 1.523 1.472 1.539 1.494 1.531 1.486 1.514 1.459 1.461 1.543 1.527
2 1.455 1.461 1.482 1.578 1.442 1.437 1.451 1.464 1.477 1.546 1.539 1.523 1.473 1.523 1.490 1.475 1.531 1.454 1.509 1.475
3 1.569 1.528 1.503 1.520 1.555 1.494 1.569 1.462 1.470 1.471 1.467 1.501 1.494 1.486 1.494 1.435 1.541 1.508 1.503 1.484
4 1.521 1.431 1.517 1.465 1.519 1.542 1.489 1.467 1.513 1.541 1.433 1.463 1.456 1.457 1.468 1.455 1.472 1.490 1.551 1.481
5 1.551 1.518 1.444 1.465 1.491 1.477 1.444 1.491 1.559 1.411 1.477 1.527 1.481 1.520 1.500 1.533 1.443 1.554 1.506 1.450
6 1.501 1.577 1.617 1.517 1.498 1.488 1.506 1.565 1.526 1.467 1.564 1.483 1.543 1.498 1.516 1.499 1.501 1.450 1.519 1.514
7 1.519 1.476 1.462 1.472 1.441 1.465 1.498 1.460 1.485 1.556 1.449 1.511 1.477 1.500 1.518 1.453 1.519 1.422 1.607 1.504
8 1.503 1.492 1.483 1.476 1.518 1.438 1.530 1.544 1.512 1.435 1.443 1.506 1.502 1.453 1.544 1.465 1.435 1.410 1.505 1.516
9 1.423 1.490 1.482 1.494 1.481 1.482 1.509 1.516 1.451 1.492 1.456 1.437 1.500 1.496 1.524 1.596 1.460 1.507 1.452 1.547
10 1.470 1.558 1.489 1.545 1.531 1.482 1.514 1.511 1.510 1.519 1.526 1.536 1.498 1.545 1.535 1.551 1.408 1.516 1.508 1.501
11 1.498 1.615 1.431 1.485 1.561 1.516 1.479 1.523 1.422 1.516 1.474 1.542 1.452 1.525 1.509 1.496 1.540 1.522 1.526 1.499
12 1.517 1.528 1.450 1.456 1.515 1.557 1.440 1.576 1.419 1.491 1.489 1.437 1.450 1.478 1.527 1.508 1.500 1.515 1.483 1.527
13 1.430 1.523 1.556 1.514 1.466 1.551 1.413 1.502 1.491 1.468 1.594 1.580 1.527 1.481 1.473 1.507 1.491 1.478 1.502 1.512
14 1.500 1.481 1.468 1.558 1.456 1.566 1.502 1.505 1.492 1.446 1.435 1.513 1.505 1.492 1.494 1.496 1.438 1.583 1.521 1.468
15 1.474 1.479 1.461 1.444 1.531 1.529 1.524 1.569 1.470 1.549 1.497 1.518 1.479 1.499 1.461 1.535 1.474 1.545 1.531 1.491

6.  Siguiente paso: Determinar las frecuencias absolutas
(fi)
 Para el primer intervalo; ¿cuántos datos están entre
1.4065 y 1.4307?.
 Los datos que están dentro del primer intervalo están
resaltados con azul, son 9.
 Este nueve es la frecuencia absoluta para el primer
intervalo.

7.  Siguiente paso: Determinar las frecuencias absolutas
(fi)
 Este proceso se lleva a cabo para cada intervalo.
 Observa como van agregándose columnas a la tabla.

8.  Un histograma es la
representación gráfica de
la frecuencia absoluta.
9 9
35 44
56 100
70 170
69 239
35 274
17 291
6 297
3 300
Límiteinferior Límitesuperior
1.4065
Fi Fai
1.4307
1.4549
1.4792
1.6245
Clasesocategoríasintervalos
1.5518
1.5761
1.6003
1.5034
1.5276
1.4307
1.4549
1.4792
1.5034
1.5276
1.5518
1.5639
1.5882
Marcasdeclase
1.5761
1.6003
Xi
1.4186
1.4428
1.4671
1.4913
1.5155
1.5397
1.6124
0
10
20
30
40
50
60
70
80
1.3500 1.4000 1.4500 1.5000 1.5500 1.6000 1.6500

9.  Determinar las frecuencias acumuladas (fai)
 La primera frecuencia acumulada es igual a la
absoluta.
 De la segunda en adelante se van sumando como se
muestra en la tabla.
 Este proceso se lleva a cabo para cada intervalo.

10. El primer valor es
igual a la
frecuencia absoluta
+
= Frecuencia acumulada
anterior más
frecuencia absoluta
actual:
9+35=44
Frecuenciaabsoluta Frecuenciaacumulada
Fi Fai
9
35
56
70
9
44
100
170

11.  Así sucesivamente
Frecuencia
acumulada
anterior más
frecuencia absoluta
actual:
44+56=100+
=
Frecuenciaabsoluta Frecuenciaacumulada
Fi Fai
9
35
56
70
9
44
100
170

12. La última
frecuencia
acumulada
debe ser igual
al número de
datos.
9 9
35 44
56 100
70 170
69 239
35 274
17 291
6 297
3 300
Límiteinferior Límitesuperior
1.4065
Fi Fai
1.4307
1.4549
1.4792
1.6245
Clasesocategoríasintervalos
1.5518
1.5761
1.6003
1.5034
1.5276
1.4307
1.4549
1.4792
1.5034
1.5276
1.5518
1.5639
1.5882
Marcasdeclase
1.5761
1.6003
Xi
1.4186
1.4428
1.4671
1.4913
1.5155
1.5397
1.6124

13.  Paso siguiente :Determinar las frecuencias relativas
(fri)
 La frecuencia relativa se calcula dividiendo la
frecuencia absoluta (fi) entre el número de datos, en
este caso, 300.
 La primera frecuencia relativa es:
 Fri= 9/300=0.03

14.  Determinar las frecuencias relativas (fri)
 Se agrega una columna más a la tabla para anotar las
frecuencias relativas.
 En ocasiones se expresa la frecuencia relativa en
términos de porcentaje, para la primera sería:
 Fri= 9/300=0.03 ó 3 %

15. 9/300=0.03
35/300=0.0116
56/300=0.186
 0.00116666667 aparece como 0.0116
Frecuenciarelativa
Fri
0.03
0.0116
0.186
Frecuenciaabsoluta Frecuenciaacumulada
Fi Fai
9
35
56
70
9
44
100
170 0.233

16. 9 9 0.03 0.03
35 44 0.116666667 0.146666667
56 100 0.186666667 0.333333333
70 170 0.233333333 0.566666667
69 239 0.23 0.796666667
35 274 0.116666667 0.913333333
17 291 0.056666667 0.97
6 297 0.02 0.99
3 300 0.01 1
Límiteinferior Límitesuperior
1.4065
Fi Fai
1.4307
1.4549
1.4792
1.6245
Clasesocategoríasintervalos
1.5518
1.5761
1.6003
1.5034
1.5276
1.4307
1.4549
1.4792
1.5034
1.5276
1.5518
1.5639
1.5882
Marcasdeclase
1.5761
1.6003
Xi
1.4186
1.4428
1.4671
1.4913
1.5155
1.5397
Fri Frai
1.6124

17.  Determinar las frecuencias relativas (fri)
 Las frecuencias relativas pueden usarse con facilidad
para trazar una gráfica circular.

18.  Anotando las
marcas de clase
como referencia y
escribiendo la
frecuencia
relativa en
formato de
porcentaje
podemos tener
mayor claridad
acerca de los
datos.
3%
11%
19%
23%
23%
12%
6%
2% 1%
Gráfica circular
1 2 3 4 5 6 7 8 9

19.  Determinar las frecuencias relativas acumuladas (frai)
 En forma similar a la frecuencia acumulada, la primera
frecuencia relativa acumulada es igual a la primera
frecuencia relativa.
 La segunda (frai) es igual a la primera (frai) más la
segunda (fri)
 Observa la columna que se agrega a la tabla.

20.  La última frecuencia relativa acumulada debe ser igual a uno.
9 9 0.03 0.03
35 44 0.116666667 0.146666667
56 100 0.186666667 0.333333333
70 170 0.233333333 0.566666667
69 239 0.23 0.796666667
35 274 0.116666667 0.913333333
17 291 0.056666667 0.97
6 297 0.02 0.99
3 300 0.01 1
Límiteinferior Límitesuperior
1.4065
Fi Fai
1.4307
1.4549
1.4792
1.6245
Clasesocategoríasintervalos
1.5518
1.5761
1.6003
1.5034
1.5276
1.4307
1.4549
1.4792
1.5034
1.5276
1.5518
1.5639
1.5882
Marcasdeclase
1.5761
1.6003
Xi
1.4186
1.4428
1.4671
1.4913
1.5155
1.5397
Fri Frai
1.6124

21.  Determinar las frecuencias relativas acumuladas (frai)
 Si trazamos una gráfica de líneas con la frecuencia
relativa acumulada que cumpla ciertas condiciones
recibe el nombre de ojiva.

22. 0
50
100
150
200
250
300
350
1.4000 1.4500 1.5000 1.5500 1.6000 1.6500
Series1
Series2

23. Esto es todo para la elaboración de
frecuencias.
Espero y les halla podido ser de ayuda
esta presentación
Saludos.