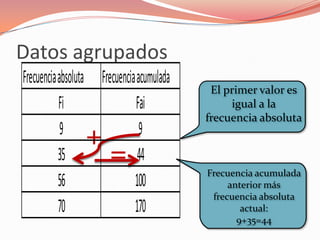
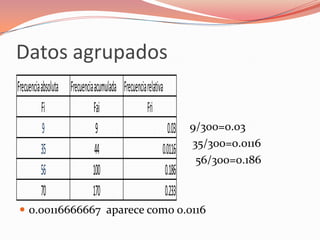
El documento explica los pasos para calcular las frecuencias de un conjunto de datos agrupados: 1) calcular las marcas de clase para cada intervalo, 2) determinar las frecuencias absolutas contando los datos en cada intervalo, 3) calcular las frecuencias acumuladas sumando las frecuencias absolutas, y 4) determinar las frecuencias relativas dividiendo las frecuencias absolutas por el número total de datos. Estos cálculos permiten representar gráficamente la distribución de frecuencias de los datos.

1. Christian Michel Álvarez Ramírez

2. Introducción
 En esta presentación les mostraré paso a paso como sacar
las frecuencias.
 Primeramente vamos a calcular las marcas de clase (xi)
 Las marcas de clase representan, cada una de ellas, todos
los datos contenidos en el intervalo correspondiente.
 Se calculan promediando los límites inferior y superior de
los intervalos reales como se muestra en la diapositiva
siguiente.
 En el primer intervalo:
 1.4065+1.4307/2=1.4186

3. Datos agrupados marcas de clase representan,
Las 
Clases o categorías intervalos Marcas de clase cada una de ellas, todos los datos
Límite inferior Límite superior Xi contenidos en el intervalo
1.4065 1.4307 1.4186 correspondiente.
1.4307 1.4549 1.4428  Al tomar la marca de clase para
1.4549 1.4792 1.4671 efectuar todos nuestros cálculos
1.4792 1.5034 1.4913 vamos a perder un poco de
1.5034 1.5276 1.5155 exactitud.
1.5276 1.5518 1.5397  Es como si afirmáramos que
1.5518 1.5761 1.5639 todos los datos en un intervalo
1.5761 1.6003 1.5882 son iguales a la marca de clase.
1.6003 1.6245 1.6124

4. Datos agrupados
 Siguiente paso: Determinar las frecuencias absolutas
(f i)
 Esta parte del proceso es un tanto laboriosa cuando se
realiza a mano, ya que se debe contar para saber
cuántos datos están dentro de cada intervalo.
 Para el primer intervalo; ¿cuántos datos están entre
1.4065 y 1.4307? .

5. Datos agrupados
12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1.534 1.448 1.503 1.472 1.452 1.506 1.552 1.526 1.482 1.523 1.472 1.539 1.494 1.531 1.486 1.514 1.459 1.461 1.543 1.527
2 1.455 1.461 1.482 1.578 1.442 1.437 1.451 1.464 1.477 1.546 1.539 1.523 1.473 1.523 1.490 1.475 1.531 1.454 1.509 1.475
3 1.569 1.528 1.503 1.520 1.555 1.494 1.569 1.462 1.470 1.471 1.467 1.501 1.494 1.486 1.494 1.435 1.541 1.508 1.503 1.484
4 1.521 1.431 1.517 1.465 1.519 1.542 1.489 1.467 1.513 1.541 1.433 1.463 1.456 1.457 1.468 1.455 1.472 1.490 1.551 1.481
5 1.551 1.518 1.444 1.465 1.491 1.477 1.444 1.491 1.559 1.411 1.477 1.527 1.481 1.520 1.500 1.533 1.443 1.554 1.506 1.450
6 1.501 1.577 1.617 1.517 1.498 1.488 1.506 1.565 1.526 1.467 1.564 1.483 1.543 1.498 1.516 1.499 1.501 1.450 1.519 1.514
7 1.519 1.476 1.462 1.472 1.441 1.465 1.498 1.460 1.485 1.556 1.449 1.511 1.477 1.500 1.518 1.453 1.519 1.422 1.607 1.504
8 1.503 1.492 1.483 1.476 1.518 1.438 1.530 1.544 1.512 1.435 1.443 1.506 1.502 1.453 1.544 1.465 1.435 1.410 1.505 1.516
9 1.423 1.490 1.482 1.494 1.481 1.482 1.509 1.516 1.451 1.492 1.456 1.437 1.500 1.496 1.524 1.596 1.460 1.507 1.452 1.547
10 1.470 1.558 1.489 1.545 1.531 1.482 1.514 1.511 1.510 1.519 1.526 1.536 1.498 1.545 1.535 1.551 1.408 1.516 1.508 1.501
11 1.498 1.615 1.431 1.485 1.561 1.516 1.479 1.523 1.422 1.516 1.474 1.542 1.452 1.525 1.509 1.496 1.540 1.522 1.526 1.499
12 1.517 1.528 1.450 1.456 1.515 1.557 1.440 1.576 1.419 1.491 1.489 1.437 1.450 1.478 1.527 1.508 1.500 1.515 1.483 1.527
13 1.430 1.523 1.556 1.514 1.466 1.551 1.413 1.502 1.491 1.468 1.594 1.580 1.527 1.481 1.473 1.507 1.491 1.478 1.502 1.512
14 1.500 1.481 1.468 1.558 1.456 1.566 1.502 1.505 1.492 1.446 1.435 1.513 1.505 1.492 1.494 1.496 1.438 1.583 1.521 1.468
15 1.474 1.479 1.461 1.444 1.531 1.529 1.524 1.569 1.470 1.549 1.497 1.518 1.479 1.499 1.461 1.535 1.474 1.545 1.531 1.491

6. Datos agrupados
 Siguiente paso: Determinar las frecuencias absolutas
(f i)
 Para el primer intervalo; ¿cuántos datos están entre
1.4065 y 1.4307?.
 Los datos que están dentro del primer intervalo están
resaltados con azul, son 9.
 Este nueve es la frecuencia absoluta para el primer
intervalo.

7. Datos agrupados
 Siguiente paso: Determinar las frecuencias absolutas
(f i)
 Este proceso se lleva a cabo para cada intervalo.
 Observa como van agregándose columnas a la tabla.

8. Datos agrupados  Un histograma es la
Clases o categorías intervalos Marcas de clase representación gráfica de
Fi Fai la frecuencia absoluta.
Límite inferior Límite superior Xi
1.4065 1.4307 1.4186 9 9 80
1.4307 1.4549 1.4428 35 44 70
1.4549 1.4792 1.4671 56 100 60
50
1.4792 1.5034 1.4913 70 170
40
1.5034 1.5276 1.5155 69 239
30
1.5276 1.5518 1.5397 35 274 20
1.5518 1.5761 1.5639 17 291 10
1.5761 1.6003 1.5882 6 297 0
1.3500 1.4000 1.4500 1.5000 1.5500 1.6000 1.6500
1.6003 1.6245 1.6124 3 300

9. Datos agrupados
 Determinar las frecuencias acumuladas (fai)
 La primera frecuencia acumulada es igual a la
absoluta.
 De la segunda en adelante se van sumando como se
muestra en la tabla.
 Este proceso se lleva a cabo para cada intervalo.

10. Datos agrupados
Frecuencia absoluta Frecuencia acumulada
El primer valor es
Fi Fai igual a la
frecuencia absoluta
9 9
+
35 = 44 Frecuencia acumulada
56 100 anterior más
frecuencia absoluta
70 170 actual:
9+35=44

11. Datos agrupados
Frecuencia absoluta Frecuencia acumulada Frecuencia
Fi Fai acumulada
anterior más
9 9 frecuencia absoluta
35 + 44
actual:
44+56=100
56 = 100
 Así sucesivamente
70 170

12. Datos agrupados
Clases o categorías intervalos Marcas de clase
Fi Fai
Límite inferior Límite superior Xi
1.4065 1.4307 1.4186 9 9
1.4307 1.4549 1.4428 35 44
1.4549 1.4792 1.4671 56 100 La última
1.4792 1.5034 1.4913 70 170 frecuencia
1.5034 1.5276 1.5155 69 239 acumulada
1.5276 1.5518 1.5397 35 274 debe ser igual
1.5518 1.5761 1.5639 17 291 al número de
1.5761 1.6003 1.5882 6 297 datos.
1.6003 1.6245 1.6124 3 300

13. Datos agrupados
 Paso siguiente :Determinar las frecuencias relativas
(fri)
 La frecuencia relativa se calcula dividiendo la
frecuencia absoluta (f i) entre el número de datos, en
este caso, 300.
 La primera frecuencia relativa es:
 Fri= 9/300=0.03

14. Datos agrupados
 Determinar las frecuencias relativas (fri)
 Se agrega una columna más a la tabla para anotar las
frecuencias relativas.
 En ocasiones se expresa la frecuencia relativa en
términos de porcentaje, para la primera sería:
 Fri= 9/300=0.03 ó 3 %

15. Datos agrupados
Frecuencia absoluta Frecuencia acumulada Frecuencia relativa
Fi Fai Fri
9 9 0.03 9/300=0.03
35/300=0.0116
35 44 0.0116
56/300=0.186
56 100 0.186
70 170 0.233
 0.00116666667 aparece como 0.0116

16. Datos agrupados
Clases o categorías intervalos Marcas de clase
Fi Fai Fri Frai
Límite inferior Límite superior Xi
1.4065 1.4307 1.4186 9 9 0.03 0.03
1.4307 1.4549 1.4428 35 44 0.116666667 0.146666667
1.4549 1.4792 1.4671 56 100 0.186666667 0.333333333
1.4792 1.5034 1.4913 70 170 0.233333333 0.566666667
1.5034 1.5276 1.5155 69 239 0.23 0.796666667
1.5276 1.5518 1.5397 35 274 0.116666667 0.913333333
1.5518 1.5761 1.5639 17 291 0.056666667 0.97
1.5761 1.6003 1.5882 6 297 0.02 0.99
1.6003 1.6245 1.6124 3 300 0.01 1

17. Datos agrupados
 Determinar las frecuencias relativas (fri)
 Las frecuencias relativas pueden usarse con facilidad
para trazar una gráfica circular.

18. Datos agrupados  Anotando las
marcas de clase
Gráfica circular
1 2 3 4 5 6 7 8 9
como referencia y
escribiendo la
2% 1%
frecuencia
6%
3%
11%
relativa en
12% formato de
19%
porcentaje
podemos tener
23%
mayor claridad
23% acerca de los
datos.

19. Datos agrupados
 Determinar las frecuencias relativas acumuladas (frai)
 En forma similar a la frecuencia acumulada, la primera
frecuencia relativa acumulada es igual a la primera
frecuencia relativa.
 La segunda (frai) es igual a la primera (frai) más la
segunda (fri)
 Observa la columna que se agrega a la tabla.

20. Datos agrupados
Clases o categorías intervalos Marcas de clase
Fi Fai Fri Frai
Límite inferior Límite superior Xi
1.4065 1.4307 1.4186 9 9 0.03 0.03
1.4307 1.4549 1.4428 35 44 0.116666667 0.146666667
1.4549 1.4792 1.4671 56 100 0.186666667 0.333333333
1.4792 1.5034 1.4913 70 170 0.233333333 0.566666667
1.5034 1.5276 1.5155 69 239 0.23 0.796666667
1.5276 1.5518 1.5397 35 274 0.116666667 0.913333333
1.5518 1.5761 1.5639 17 291 0.056666667 0.97
1.5761 1.6003 1.5882 6 297 0.02 0.99
1.6003 1.6245 1.6124 3 300 0.01 1
 La última frecuencia relativa acumulada debe ser igual a uno.

21. Datos agrupados
 Determinar las frecuencias relativas acumuladas (frai)
 Si trazamos una gráfica de líneas con la frecuencia
relativa acumulada que cumpla ciertas condiciones
recibe el nombre de ojiva.

22. Datos agrupados
350
300
250
200
Series1
Series2
150
100
50
0
1.4000 1.4500 1.5000 1.5500 1.6000 1.6500

23. Gracias por su atención
Esto es todo para la elaboración de
frecuencias.
Espero y les halla podido ser de ayuda
esta presentación
Saludos.