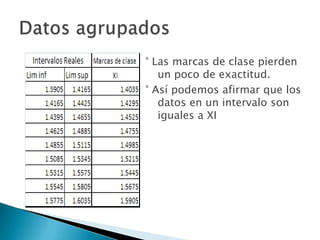
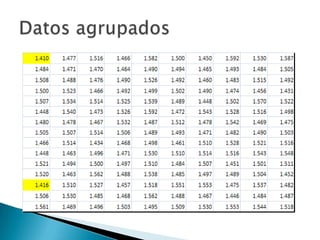
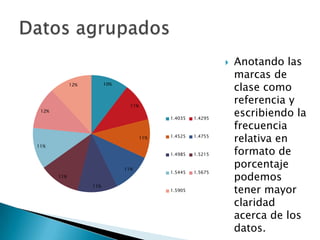
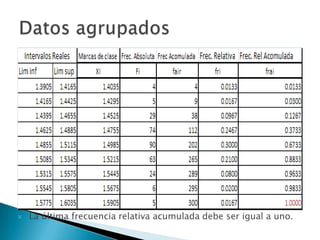
Este documento explica paso a paso cómo construir una tabla de datos agrupados. Detalla los procedimientos para obtener los intervalos, marcas de clase, frecuencias absolutas y relativas, y frecuencias acumuladas y relativas acumuladas para representar gráficamente los datos agrupados.

1. Nancy Leal Ramírez.
Grupo: 2°A

2.  En esta presentación se construye una tabla
de datos agrupados paso por paso.
 El objetivo es explicar paso por paso, las
operaciones para resolver, problemas de
datos agrupados.

3.  Procedimiento para datos agrupados
 Ejemplo:
 A continuación vamos a completar la tabla
estadística, con los siguientes datos
agrupados, con 8 intervalos.

6.  En la primera parte de esta presentación
obtendremos, los intervalos aparentes, dado
que a los limites inferiores, se sumará el
tamaño del intervalo, luego en los limites
sup. Restaremos 0.001 ya que estamos
utilizando números de 3 decimales.
 En la tabla debemos observar lo siguiente:
 Tomando en cuenta: Max= 1.598 y el Min=
1.392

7. 1 1.391 1.416
1.417 1.442
2 1.44 1.465
3 1.463 Los cuatro valores 1.488
4 1.486 Cumplen las 1.511
5 1.509 Condiciones. 1.534
6 1.532 1.557
7 1.555 1.58
8 1.578 1.603

8.  Quinto paso:
 Se obtuvieron los intervalos reales que se
muestran en la diapositiva siguiente.

9. 1 1.3905 1.4165
1.4165 1.4425
2 1.4395 1.4655
3 1.4625 1.4885
4 1.4855 1.5115
5 1.5085 1.5345
6 1.5315 1.5575
7 1.5545 1.5805
8 1.5775 1.6035

10.  Sexto paso:
 Para calcular las marcas de clase, es decir que
se va a sumar los lim. Inf. Y lim sup, reales y
se divide en 2.
 Ejemplo:
1.3905 + 1.4165 = 1.4035
2

11. ° Las marcas de clase pierden
un poco de exactitud.
° Así podemos afirmar que los
datos en un intervalo son
iguales a XI

12.  Séptimo paso: Determinar las frecuencias
absolutas (fi)
 Esta parte del proceso es un tanto laboriosa
cuando se realiza a mano, ya que se debe
contar para saber cuántos datos están dentro
de cada intervalo.
 Para el primer intervalo; ¿cuántos datos están
entre 1.3905 y 1.4165? (o entre 1.391 y
1.416)

15.  Séptimo paso: Determinar las frecuencias
absolutas (fi)
 Para el primer intervalo; ¿cuántos datos están
entre 1.3915 y 1.4065? (o entre 1.392 y
1.406 )
 Los datos que están dentro del primer
intervalo están resaltados con amarillo, son 4.
 Este dos es la frecuencia absoluta para el
primer intervalo.

16.  Séptimo paso: Determinar las frecuencias
absolutas (fi)
 Este proceso se lleva a cabo para cada
intervalo.
 Observa como van agregándose columnas a
la tabla.

17.  Un histograma es la
representación
gráfica de la
frecuencia absoluta.

18. ° Octavo paso: Determinar las frecuencias
acumuladas (fai)
° Esta se obtiene sumando la frecuencia
acomulada más la frecuencia absoluta.
Ejemplo:

19. + El primer valor es igual a
la frecuencia absoluta
=
Frecuencia acumulada
anterior más frecuencia
absoluta actual:
4 + 5=9

20. La última
frecuencia
acumulada
debe ser
igual al
número de
datos.

21. Para el noveno paso lo que se tiene que hacer
es dividir la frecuencia absoluta entre el
numero de datos que en este caso son 300

22. Fri=4/300
Fri=5/300
Fri=29/300

24.  Las frecuencias relativas pueden usarse con
facilidad para trazar una gráfica circular y
como tienen el mismo comportamiento que la
frecuencia absoluta, pueden etiquetarse las
divisiones de la gráfica como frecuencias
absolutas o relativas.

25. Frecuencia Absoluta
Frecuencia Relativa
0.0167 0.0200 2% 2% 2% 1%
0.0200 0.0133
0.0933
8% 9%
0.0800
21%
25%
0.2100
0.2467
30%
0.3000
 Ambas gráficas son idénticas, sólo las etiquetas
de datos son diferentes: en una están las
frecuencias relativas y en otra las absolutas.

26.  Anotando las
marcas de
12% 10%
clase como
11%
referencia y
12%
1.4035 1.4295
escribiendo la
frecuencia
11% 1.4525 1.4755
relativa en
11%
1.4985 1.5215 formato de
11%
porcentaje
podemos
1.5445 1.5675
11%
tener mayor
11%
1.5905
claridad
acerca de los
datos.

27. ° Décimo paso paso: Determinar las frecuencias
relativas acumuladas (frai)
° Se obtiene pasando la misma cantidad de la
frecuencia relativa, a la columna de la
frecuencia relativa. acomulada, y se va
sumando, con la frecuencia relativa.

28.  La última frecuencia relativa acumulada debe ser igual a uno.

29.  Décimo paso paso: Determinar las
frecuencias relativas acumuladas (frai)
 Si trazamos una gráfica de líneas con la
frecuencia relativa acumulada que cumpla
ciertas condiciones recibe el nombre de ojiva.

30. 1.2000
1.0000
0.8000
0.6000
Series1
0.4000
0.2000
0.0000
1.4035 1.4295 1.4525 1.4755 1.4985 1.5215 1.5445 1.5675 1.5905

31. Si hacemos el ejercicio con 15 intervalos al
momento de compara las cuatro esquinas no
nos va a coincidir ya que el numero de los
limites inferiores aparentes, es mayor al
número mínimo de nuestros datos observe la
grafica siguiente:

32. Ejercicio Equivocado.
1 1.392 1.405
2 1.406 1.419
3 1.42 1.433
4 1.434 1.447
5 1.448 1.461
6 El int. 15 no
1.462 1.475
cumple con la
7 1.476
condición. Es 1.489
8 1.49 mayor que el 1.503
9 1.504 valor Máx. 1.517
10 1.518 1.531
11 1.532 1.545
12 1.546 1.559
13 1.56 1.573
14 1.574 1.587
15 1.599 1.601

33. http:/nancylucrecia.bligoo.com.mx/