El documento resume conceptos fundamentales de física como el universo, las galaxias, la teoría del Big Bang, la física clásica y moderna, las partículas elementales y las interacciones fundamentales. Explica que el universo contiene billones de galaxias y cada galaxia billones de estrellas. La física clásica estudia fenómenos sensoriales mientras que la física moderna estudia fenómenos a nivel atómico. Las partículas elementales incluyen leptones, quarks y hadrones

![I --
- 11,
.&&, ¡&c"¿rlemvaü*l* 0""u'
i{e*:l
g¿'",.§o^L e¡* LL'- ¿^ tL
TJNIVF,RSO: I:s el conju¡to form¿¡do ¡xrr loda la maferia, energía y espacio en expansión qué existe. Se estima que el universo contiene 1ffi mil
rnilkrnes de galerxiars y cada una coniiene 100 mil millones de eskellas. El sol es sólo t¡na estrella de una de las galaxias.
Atlenl¿is ric errrellas y pltrneras. las 1¡aiaxias conlienen cúmulos de eshellas. hidrógeno atómico. hidrógeno molecular, moléculas complejas,
cornpuestos de hidrógeno. nitr<igeno, cartxrno, silicio, entre otros elementos, y rayo§ cósmicos.
BIG-IIANG.- (iran explosión que ocunió hace 18000 M de años (Según informe NASA.Mayo 1999). l-a edad det universo está e§timada en
12000 M de nrios (M millones)
I-AS GAIAXIAS
{¡RI¡T¡O GILTLE{,
fflu",'¿
i-
'
I
I
lJn¿ 1¡zrlaxia es un (rrupo de v¿rrios rniles de millones «le estrellas y de material interestelar sosteniclo por la gravedad. Cada gá@:iá forma una isla
lrrnrin<>sa perdida en el inmenso nl¿lr neflro del universo.
itt',,. :=
jr'r']
, LA vÍA rÁcree J,
Nueslro sistem¿:¡ solar esl/r en una g¡alaxia que se den<¡mina víali,atea. Vista desde la tiena forpa.¡nrc;¡tübe.pálida:$i#iecha
que cruza el cielo
nodurno ,le un lado ¿r olro. Nueslr¿r galaxia está compuesta de 200 a 300 mil millones dq.¿-fr¿lla§.que {orman un disco grande con brazos
esPir;rles. lienelit)()0miltr,nes{lp¿r)ios.nrientrasqueel sistemasolarylatierratienecercade 460Omill<¡nesdeaños.pareceunpequeñoarro!¡o
rle ler:he. que es lo q¡e inspirri a furs anti.<¡uos g¡rieJ¡os para llamarla vía lácfp¿,cinco mil millcnes de anos atrás aproximadamente, el sisiema solar,
::.., ,. --.:,,,.:
No hatría olra cosa que una inmens¿r nut¡e de polvo y gas difusa que .giraba §o-b' $misma. Mii,s- tardp,,nació el sol, y luego los nueve planetas,
entre ellos la tierra, los cuales se fomraron como bolas de nieve por aglomeración' Ia materia en el ihterior de esta nebulosa original
'
''iil'
LA F.ÍSICA ll,f IySYCS Nohraler.o) '1 "*, - -
estudia las leyes que detarminan la estructura del univ.erso con respec[.-.e$á1:lati4$gria y la energiá de la que está constituido
'.l
'= " ':i""'4'"tl
''
¡MPOITTANCIA Y PARTES DF: I-A F'ÍSICA ''::' 1",j-., '
[)n solo üist¿vo a las conquisiars ¿e nues¡:a. civiii., ción,
"r.;¡üOig.nla-para
revelarnbs la trascendencia de l¿¡ cienci¿r física: la luz eléctrica, el
raclio, el tc¿léfon<¡, la releviskin. el ¿¡utornóvil, el avií¡n. los reacié@nucleares, lo§'satélites ar]ificiales, etc., son todos productos de la Física,
ciiyo estLrclir> es ap¿lsion¿)nle y de 1¡r;rn inierés.
" '
't'l" ttt'
MÉT0D() CIENTÍFICO ,]ii .:,.. .-
I-a f:í-.ica <:omo ciencia consiste en la clescripción:oráeñ'#á,.coherente yr§istemática de los fenórnencx; naturale-s; para lograr esa descripción el
invesligzrdor r<¿ali,,r rrna serie <ie <;peraciones qug constit dIi_U..,.:_1,e:tu-""
"l
método científico.
-r'
It:l método cir:ntífico consiste ¿n:.;ál esarrollo de:'l¿8 siguientes operaciones.
i . Otrsewa<:iíjn y experiment:rcitin
2. I-lipótesis y teoría. :.
13 Organizacitin le..yes
/l VeIncaclon.
¿CÓMO SE DIVIT,E LA.FÍSICA? ,.... .
[:xjslen <iivers¿rs fonnas..rle,r]iúiáitJa,i:lsicá I)es<le e[ punto de vista histórico, la Física se puede dividir en: Física Clásica y Física Modema.
¡.nsitler¿indo las ziplicaciones especÍficas <le Ia Física, podemos divídirla en: Física de sólidos, Física de plasma, Física nuclear, Física de fluidos
i).'1ec;inica de fluidr¡s). Físic¿r de Ia ¿rtmósfer¿¡ (Meteorolo.c¡ía), Biofísica, etc.
FisICA clÁslcn Y FíslcA MoDERNA
4) I'-ísica Clásica
I.a l:ísica clásica eslu<lia k¡clos kis'fenórnenos que tienenl que ver óon nuestras impresiones sensoriales: de la observación de los
'rovimienlos
surgki Ia Mec¿inica; del iacto su4¡ió la 1'ermofísica; de la audición surgió [a Acústica; de la visión surgió la óptica; etc. En la
Irísic¿i clársic¿r, <lesde el punto cle vista de la Mecánic¿¡, son válidas las leyes de Newton y desde el punto de vista elechomagnético son
v¿ilkl¿rs l;rs
"(
u¿rcion(rs rle M¿xwell.
para el estudio sislemáLico tlel estudk¡ cle la l.ísica clásica, ésta se divicle en 5 partes principales, como se puede ver en el siguiente cuadro.
W"
.i'{lr llienes.el Patcn§iol, N,asatro§ lq Exgerie4cia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-2-320.jpg)
![r
MECÁNIIA
ü f-ís¡c¿ Modema
Antes de 1900, las leyes de Newto¡,en Mecánica, las.écuaciones dá]Ma1we1lrén E1éctrornagnetlsmo. las leyes de la termodinámica, y la
-leoría
Cinética Molecular cle los gáses, tuvié?on sucpió en la eiplieación de,rn,ü.qp enómenos físicos. P"ero, con el descubrimiento de los
electrones por fhomson (1897),'la Física Clásica e.mpe.zó a."tam.b¿rlear'1 iiorqüe tói científicos n<; lograban-explicar el movimiento de los
electrones clentro rlel átomo uiando las leye.s. ciásic.r",l. iu F{9isa,- P-e,I..¡fetizmente e¡i1900, cuando Max Planck estat¡a estudiando la
emisión y absorción <le energía de un cuerpó nu,¡rá, encontró ' h futá altemari.üát,p,a : que las observaciones sean coherentes con la
teoría, era necesario
".I-i.,ü"
"furMáietr1es
"*iit*t. -q,!.b$9;
energláün rma.d¡éo*nua, en paqu€les pequeños y discretos llamados
,,cuantos,,o ,,fotones". Estaidearci la'qued,io'órisen ál.na'¿i¡ñientoüá,t6&oríaCuáhtica de Planck. Con,.e¡ta teoría se pudo explicar
muchos fenórnenói oué,dcunen a nivel {_e la estructura del q!o,ino,- ,,i,.::i.;li]i,j,.,
É,r,,j -,,...
otra teorÍa que revolucionó la Mecá¡íi'L r:s la Teoriá]:-, .ReÉtividad ¿i¿:giqü*,i";i ói;uesto en 1905-'Bhreóría.stiig]ó debido a las
contradicciones que se encontraron éuancit; lr"ru",á liiááx lai',Ieyes du'Ñial^rt.n', pura movimientos con,vélocidadeq.d6tnparables a la
velocidad de la luz (300 000 kmis)-
. iilríri':$.',, i: .--.:l;;'
§**ee*mcn:'
La Física moderna estudia los fenómenos.que no son percibidos por n-ue,s,t¡g,s sentidos.directamente, donde las-leWé'de Newton y las ecuaciones
de Maxwell no son válidas, siendo neceáti*u reformulacién C.o¡r la Ffsicá clásica no''fluede.n ser explicados"'muchos fenómenos, que ocufien a
nivel de la estnretura del átomo. I-a Física clásica tampoco,lpliÚáá se.tiáiicadu u movimid tós de pa-rtfuulas con velocidades comparables con la
velocidad de la luz. Debido a esta
,,inbapacicla-d" ae L fis.i§@tasicá;iurgen.laleor.ía,',eirántica V,..'t.},ieoría de la Relatividad, éstas actualmente
constituyen la base de [a Física modern , snt¡ün tg Física m-sdi&a, las leyes de Nr$tenrel.oiFrticulares de la Física Relativista y Cuántica
MAVTMIENTÜ
üNDULATü,R|fl
TEORIA CI'ANTICA
NIVELES f,STACIONARIOS
DE ENERGiAM. Planck - I900
(P Nobel l9l3) .
N. Bohr - t9l3
(P. Nobel 1922)
r, ,MECÁNICA
cuÁxtrc¡
:
./
DUALIDAD DEL
ELECfRÓN
ECUACTON DE ONDA EE
SCHÓDINGER .: .:
L.&Btuglic-1924
(P. Nobel 1929)
E, Sclródinger - I 926
PRI¡{CIPIOSiDE INCERTIDII M BRE
w. Heisemberg - 1927
(P. Nobel ls32)
fERMqr'l§le*r
FiSTcAMoEEFNA
, t900-?
MECÁNICA CIIÁXUC.I
Basada en la Teoría Cuártica de
M. Planck 1900
s¡rve para qplicar los fenómenos con velm¡dad
próximas a la velddad de la luz
sirve para explicar los fenómenc a
n¡ve¡ de la estructura del átomo.
llbícanos en la Av, De Ia euftura7076 (frentc a la UNSMC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-3-320.jpg)

![r"'
-
l,ffies{¡TuD§§ fí€I 6/t"8,-SU
MAGNITUD I.íSICA.- [::s lodo Aquetlo que puerlg ser cuantificaclo ylo comparado y que representa a aiguna propiedatl lísrca de la materia
MF:DIR. [i comparar <ios rnatgnitudes de la misma especie donrle el ente de comparación es la unidad de rnedida.
CIASIFICACIÓru Nt, I.AS MAGNITUDIiS.
Li.rs magnilucles físicas puederr cl..sificarse tle dos fotmas'
L. Por su origen.
@es.
inlernacionales.
@.Son' fundamentales.
Son aquellas cuyas unidades se han eleg¡iclo como fundamentales de acuerclo a los convenios
aquellas cuyas unidades se forman de una c<¡mbinación de las unidades cle las magnitudes
S¡§IE¡I.LD¡i.¡JD¡IDráF-é. t ts el c<>njunto
oblienen las rnal¡nitudcs derivadas.
Por su natural.eza.
at-.,,.M4o+itugl§: q;sslsees- Estas magnitu<les sok¡ necesitary.'de un número real v una
:Tlq* .!: T"l*^lii ::1 1l]l::1"1i:ts. l:slas magnitu<les aparte de 'ienei un número y una unidad física necesitan de una rllrt'r:ción y sentido
-.n
ordenadO'y coherente de unidades fijan las magnitudes básicas o fundamt'nt¿'les y luego se
(S.I.). Ls eirprerducto final de,la eveluciór1'lót¡ic4del antiguo sistema métrico dccimal o MI§,
que incrementzrrlo en cu¿rtro uniclades ro c,rnúl"rte ahora en .el sisterna l¿sal de unida{g, e casi todgs los países del mundo'
,":::' '.: :
S.t. ¿e unicla¿es en el peru se re5¡lamentír mediante,la üü"ZgSOO:ptór"u1gada elSfilÉDi¿romure,de 198?g que4ó establecido e[ sistemalegal de
urid¿rrtes <re medicia,i"t p;;-idii;ilpi. i,a.si. *tá áxo*áa",gertus,,1ffili$it a". !§i.asj1áug,,r6i'conve¡9ion
internacional,se kata,de
-"*ñütriii*
MA9NIU¡) UNIDAD g,;.,:" sNIt( lLO
nr$iii iiu""
ñrwr6-§6liüo^-
tr{
r
ANÁLISIS DIMENSIONAL
'[rata ¿e las relaciones maternáticas de las {imensiones de las magnitudes físicas. , .r'r mula dimensional o dimensión de una magnitud derivada
está represenl.dtr por un monomio forma<lo por el producto de los símbok¡s t ' t. magnitudes fundamentales elevadas a ciertas potencias
enter¿rs o frerccionarias, positivos o negpl.ivos.
Así la fórmula dimensional de la magnitud derivada X, tendrá la forma.
X , , Símbolo de la mágnitud o unidad X
lx I "'' [-:.cuación dimensional de "X".
cd
Mol
ptrra estar bien <lefiprrfás
i , .¡n'., . :::.4
MAGNITUDES SUPLEMI'N T RIAS
[x]= L¿M
Ilbícanos en la Av. De lq Cultura7076 (frente a la UNSAAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-5-320.jpg)
![-
g¡A A.uelernia Gallleo-;N; Za w¡¿. $wdc. G}I'T.IPO GALILEO
PROPIEDADES DE I.qS F,CUACIONES DIMENSIONAI-ES.
I-as ecuaciones dimensionales, cumplen con las leyes del álg¡ebra; a excepción de [a suma o rest¿l
¡ l,eacl=[z]lrl[cl
, I A" l.- lrl
Dotl&: A y Il son das rrognitudes físicas cu:alqtioo
Las ecu¿rciones dimensionales de los números. ángulos, funciones kigonométricas, funciones logarífnicas, etc. es igual a [a unidad
Estas mag¡niludes se denominan adimensionales.
, I ef _[e)
Irl-lal
, lt;'1.1o4'r,
["l
[-as ecuaciones dimensionaleS de las constantes numéricas son igual a la unidad.
,lo 3,1416l I { fe..,2,71...1..,1
Las ecuaciones dirnensionales de las constantes físicas, es diferente a la unidad.
I lg = aceleración tle la gravedad
),r1 .,=
3. La ecuación dimensional de todo exponente y argumento es igual a la unidá&¡*: :'.
Toda igualdad matemática que expresa la relación e4f-íá tas rliferentes m+ignitudes físicas, deberá tener homog¡eneidad dimensi<¡nal. Es decir, las
dimensiones de cada uno de los términos deben ser lái'mismas en ambos miembros de Ia ecuación.
, [o,zs+tl-r
, lsm31" rtg53"l -l
, [,txl..,lDts(/]r r c:)l
, Iar l.-l,r-l
t IAX Dtg(BY 1 (:)l'LZEl
, l¡2zrrad
--= 360"1 .,, I
7 llogl00l=l
#
e
.&
s
s
€
ALGUNAS DE I.á§]:E€I,ACIONES DIMENSTONALES EN §,I. S.I.
MAGNITI-ID
ITISIEA
UNIDAD ,§I,IUBOLO a.»: [x] IJORMULA
:,,.t:,:
Superfip..iá o
ur"gijLl,.:
Metro
cuadrado
2
tn L, (Longitud)(Longitud
Volumen
;B"*P,*:$,P
tn' t (Árn")(tttura)
Densidad ó
densidad
volumátrica
Kilogramo
por metro
cúbico
kg /m3 M13 *kr!:!-
Volumen
Velocidad
Metro por
segundo
ntls L7"-
r:e"S:t fgg., rrlg
'l'iempo
Aceleracién
Meho por
segundo al
cuadrado
mls?" LT-2
l/:!9!rdg,t
Tiempo
Aceleración
Angular
Radián por
segundo al
cuadrado
Rad I s2 T-2
Velocidad angular
T'iempo
Densidad lineal
Kilogramo
por metro
kg lru ML-1 -Y!:!-Lottgituds:i
t
f7-l ¡Tú Tienes el Potencial. Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-6-320.jpg)
![r'
FͧIC& T ACADEMIA GALIL§O
*
C¿rntidad de
rrlovirni¿nto
Kikrgrarno
metro por
segtrnd<>
lcgm I s MI,T'-I (Uasa)(velocidud
P¿riodo Segundo s T
'Iiempo
Nro.de oscilaciones
Frer:uencia Ylerlz, Ilz,-lls T-t
!!ig.!9,'",!!:,"!:!
'l'iempo
Fuerza, peso Newton N, -kg.ml s1 M I,T-2 ( Ua,s a) ( rt c e I e r rt c i ó n)
Presiírn P¿rsc¿rl P.- N I nt2 ML-IT-?
l"'uerzo
Area
F-nergía.
'trabajo, cakrr
Joule
;1 .¡
'U;llr' (r;uerza)(»istancia)
Potencia, flujo
de energía
Watt M1,,7'
, !:gPw
'fiempo
Oarg¡a eléctrica Couk¡mtr Cl= A.s 7'1 " (A o,.ry i e n r e
) (Tt e mp o
)
Potencial
eléctrico
Volt V'rW l',A' ytr:#: :liN _lw::r<t*!:vv
.,¡iiiii¡Por¡:¡e*l e é I e ctri c a
Capacitancia
eléctríca
Fald
..,11' , "*r".
F ,,C IV *'1rc Carga elé,itrica
;:,;,; otenaial eÍée.trico
Resistencia
elé<:.trica
Ohm Q,,,, lt I A
i].",:l il ,li
Mrlr,?+r,i
Po;tencicleléctrica,lr
Corriente électrica
[:lujo luminoso I -umen lm = cd.§ltl:,| ,J (.f e,m)riu"po), tti:'"
lluminación [-ux l¡==finlv¡f :il-'1
Flujoluminóio
----=:-tt--
'' Area
Campo
eléctrico
Volt por'"
metro
.,v lnt MLT-]I I 'P,btencial eléctrica
Distancia
Viscosidad
cinemática
Metro al
cuadrado por
seg¡undo
m2 ls üT'
'forque <;
rnomento
Newton
metro
Nnt ML'T'' (Fuerz a) (B razo de palanca)
Oaudal o gasto
Metro cúbico
por segundo m3 ls I;'T-'
(Área)(velocitlart) ó
Volumen
Tiernpo
Viscosidad
dinámica
Pascal
segundo
P.a.s rtMT-l
Capacidad
calorífica
Joule por
kelvin
JIK tMT-'@-'
C¿rlor
especifico
Joule por
kilo¡¡ramos
kelvin
Jlks.K) Er-'@-'
Campo
maenético
Tesla Nlc.v MT 2l'
;É?
s
#
EA
ubícanos en la Av.I)e la Cultura7076 (frente a la UNSAAC) fI](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-7-320.jpg)
![-
&&*ade*r§WX
l-
GftUPO GJiI.TLEO
DEFINICION DE LAS MAGNITUDES FUNDAMENTALES (S.¡.)
&letro (m).- F.l metro es la dlstancia recorrída por la luz en el vacío durant" "--"1 ---- de segundo.
299792458
Desde otro punto de vista ta defirríción moderna est¿ülece que la velocidad de la luz es deZ99 792 458 metros por segundo
Kllogramo (kg).- El kilol¡ramo es l¿¡ masa formacia por una ale¿¡ción de platino e iridio que equilibra un decímetro cúbico de agua a la
teml>eratura de 4 grados cenlígrarlos en un¿l bal¿rnz¿¡ de brwos i5¡uales.
segundo (s).- EI segundo es l¿:r duració¡r de.9.192.631 .'/70 períodos de la radiación correspondiente a,!át'kansicióiͧiiiÉt&dos iliveles
hiperfínos del estado fundamental del isótopo 133 del átomo de cesio. '...::.
- iÍlr',i",,,. , !iil{, ',,',,,,"','.¡@»,@<t,.¿ü -*-..!.!!
p 4 - *
--
--t -4 *. r.tuwbe - ! -
-.-I
Amperio (A).- F-l amperio es la intensi<lad <le una corriente eléctrica constante que. mantenida éii:áe¡s,c<¡nductq4iÉi paralelos y
rectilíneos de krngitud infinita. de sección circular y cok>cados en el vacío a una dist¿¡ncia de un. rnetrd'iénttg".¡o:óg, tro, prodüce en
dichosconductoresunafuerzai¡¡ual a2x10"7newl.onpormetrodelongitud. ,.,.t ',:." t': ;;'
Kelvín (K).- [:l grzxlo kelvh es la fracción 11273]6 de la temperartü-ra termodinámieál.{el punto lriple del agua y corresponde a la
ex¡rresión de un inlervalo de lemperalura t .
r
:t.
Candela (cd.)., l-a candela es l¿i intensidad luminosa en dirección perpnndiélúlÚ.de una superficie de 1/600.000 metros cuadrados de
un cuerpo negro a la l.emperalrrra de fuskin del platino (20451f-[;:bajo la presión <Ié:4:$1tl&25 Newton por metro cuatlrado.
,:
':"
Mol(mol). Es igual a la cantidad de sustancia quá collliene tanlas unidq iglementales'éonto átomos hay en 0,012 kg de carbono 12.
i..; !-' " -'
..
I .s."
r-
t
I
t_
PREFIJOS
Yota I Y L024
,'i,!.,. Zeta i Z 1CP'
Exa r..., E 10r8
P.e.ta P 10rs
T 1012
Giga'rrft G 10e
Mega I M 106
Kjla K 103
f clo h I(r
Deca da 10
f)eci d 10'r
Centi c 10'2
Mili m 10¡
Micro p 10{
Nano n 10-,
Pico p 10'12
Femto 10r5
Atto a 10-,0
Zepto z 10-21
Yocto v 1
f- t] ¡Tú Tienes et Potencial. Nosotros la Experiencia.,,!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-8-320.jpg)
![s"g§§üe §
P[0BLlir]IA NllO: (]l
l.a dir-nensión de [l en la siguiente expresión es:
pV Pli
(donde: p,,.,;resi<in,V' volumenyP " peso)
a) l-
tr) I-1.z'-
t1l.¿¡
d) r.- l
or) Ml-1
tlit()lSlliurl NIto: ()2
I-¿r dirnensiones cle lt erl ia expresión si1¡uiente son:
n - ,hl/<:2
l)r,lrde: j
ñ) fllas¿l
f frecuencia
lr) Ml. ''l
, ) MI."l
cI) L21 r .,.' ' ..,i ..
e ) Adirnr:nsional
Pl¡{}lll,li}IA NIt(}: (}il
I-os v¿rlores <le x a y en la si.t¡uiente ecuación ditnensiÓnálrnente ,""
col recl, r:
sienclr¡ J <¿l nrt¡ment<r tle úlerci¿i, m rn¿ls¿l, r, y r,,,, ,lislzrncias, son
rPspP( liv¿lincnlP:
a) l,l
d)l;.r;
b) 3,lJ c) 4./l
ej ?..2
Pll{}lll.llit!,1 ñlt0: {} t
l.rr rtt¡itl:z rle utta r'rt,'t,1,, psl¿r dada por la fórnula:
S (;rtl lil t b,l'
s it, nr lr ,:
(¿ crrrtlr, . N
R r;rclio
rl rii,irnr'lro
S li,¡itlez ett N
l-as dimensk;nes.ltre tier'Ien zr y tr son resp€ctivamente
d) L'l ; ML 11'
l,lt0lllllilrl NII(I: (15
L¿r ecu¿rcirin: ,S
^[(i,i;
L,¡ ili
as rlimr¡nsi<lnalrnenie c<>rrecta siendo
I: , trab¿lio
n] Iil¿ts¿l
(l ¡rceler¿rckjn
ll ;,llur;,
I-u<:1¡<; ia dirncu nsi(rn de S es:
a) (J.'l' r) 1¡1: b) I-1'' c) L 1'l
d) (l.l')r ? e) No f it:ne <lirnensiones
Pn0llllllll/r Nlt{): (Xi
Ln la siguienttu ecu¿¡cií>rl dimensiorlalmente conecta
cr:u;x:irin dirnension¿:l de x
:L ri:;it:l/:,
,:ir.l.ij...:ti:.#r,:!
c) I":Ml.l''
e) f-lMI-'l''7
I)r:nrle:
M rn¿1s¿i
^1
Lil,7'l
d) Nt:t.'7
I)eterrnine la
ti
V vtu k¡c:idad
b it,t
-'L ''t'
<t lf '1.'l'
c) ,tt,tt
Ilbícanos en ia Av. De ta CuItutuTATí (frente t¡ ta UNSAAQ ';
i r.:!"
-ru
PltOllLllMA NII{I: O7
l-a fuerz¿i de atracción F entre dos masas puntuales m1 y m2, según
la [-ey de Newlon de l¡i Gravitación Univemal. esiá dada, por:
- | lllt m.,
I K'---;-'-
r'
Siendo r la distancia que sep¿rra ambas rnasas. Las dimensiones de
la constante k en el sistem¿r técnic<> (F,L,'f) son:
i)) FI -41'
4
tr) PL 2 c) I;f-z
d) Ir'1 L4l'4 e) FLI-z
PIIOBIIIMA Nll0: {}ll
l-as dimensiones de K v C en la écuación dimensionalmente
homogénea siguiente son respecf.ivamente:
M Sen0t'
n(K' t h')
(donde M es el moment<¡ de una fuerza, e un ángulo, m una rnasa y
h una longitud).
a) I-2.'J' b) I-T-1,1'2 c) t., T-2
<1) Adimensionalmente ambas e L.,'f'2
t tt0ttlEila.Nlt(t: o$
En.:la's¡gulá¡r"- expresión los valores de x, y. z son respectivamentel
.:ii,:, ., 'r..(*, - rn;) C = alEvd'(nz+n+ 1)
lDr¡ride: iiii,=:::.l
",.m¡ ! m" sonmása§
C = velocidad de la luzul
a = aceleración angülar
'd:¡¡:dᡧidad r,,.',,=
I: : espacio. n = un número
aJ'Z;-.í-i1" ::.:.',,: b) Yr,'4,:) ¿) s, s, s.1",
PROIII,DMA NM): l0
r:ta cántidad de c¿ilgp Q que pasa .po¡ 'úna lámina de área A y
¡,,. esor.ü¡desde.'rliia t¿rnperatura T1 hacia una temperatura T2 en
-
uri tiámpo'tiestá:rtlada por la $gnsl¿nte fórmula.
..,",,.,'Q'-'x 1r2-),
b
K ',' conductividad lémrica del material.
Flall¿rr la.e-cuaci<1n dimenskrnal de K.
a¡ lxj.- trn 'á-' u) [rl' ^41'ro
'
^tIx1,.uLre stIKl
^tLr
e'ura .r u/¡ I
^
,l' Kl = M LT'0-'
PItOllLBllA NIIO: I I
- lx t vnt(vmnph
l-er expresión F ^
-'-/" t) ""'é" I es una ectración
z (log 25 + y)
homogénea, donde:
[: . fuerza
M ': MAS¿¡
h--, altura
§,.. aceletaiión.
d) Y?,4,'1
Usando partes de la ecuación.
I vz.
I.{alte I
-lx
e 1,312,2.
a) MI
d) r-
b) uur
e)M
c) mL.rl
lrlll)Ill,li,llrl ñIlO: I 2
[Jn estudiante plantea una ecu¿rción dimensionalmente correcta
para los qases expresado ¡>or:
(P qvr)U-flvz) " nRl](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-9-320.jpg)
![a
Aeader¡ria Ciali,8a o*¿7¿.
P.. presión
vr,,= velocidad promedio de las moléculas
V=. volumen del recípiente
vz=. velocidad promedio de las moléculas
n.. número de moles
R =, constante física
T= temperah.rra
Calcular
la t nl
C, L.TNE
PttOBLtllA NB0: lll
[,os resultados de Vander Waals para los gases ideales s¿ pueden
expresar mediante la ecuación:
I ---z I
I
p ,*l( - nt).- nnr
L V'I'
Dorrde:
V.., Volumen,
P'=. Presión,
T.- Temperatura absoluta
n.= número de moles
R.- Constante universal de los gases.
Considerando a la ecuación dada, dimensionalmente correcta.
I{alte ta dimensión a.la I bl
a) rr¡L2r-2N b) n¡rl c) Ur.-lr
d) uL2T-rx e) HIL'r-rN
Pn0BLDilANf,0: 14
Considere un sistema en el cual las 3 cantidades
la velocidad de. la luz- c, la masa m del protón y
GTIt'l}O G'[I-IT.EO
l¡ll()BLBilA Nltl): ltl
Se sabe que la velocidad de una onda mecánica en una cuerda en
vibración depende de l¿: fuerz¿r llamada tensión ('l') de la masa (m)
de la longitud L de la cuerda. Encontrar una fórmul¿ que pcrmita
determinar dicha velociclad.
t).,.. Eclo.=
z*
"1",,,F
PE{}Bf,tlllt ñf,O: tO
Hallar et valor de q para que la €cuasióñ sea dirr¡sr*xral¡nente
córrecta.
1ñ'- # =' r*n
a) a = 1t0o
d) a == 123"
a ).4 El"* c¡
elc:
Pf,OBT,BIIA ITI(h 20
Determine [X,Y,Z], si la 'dime¡rsixra&mg¡le
correcta:
wsenO =
a)v., l'rlT,,
Or"=
rPal ÍTNq
d) D,TNq
a) h/m2c
d) trlne
bl t;nTNo
el I;4TN0
b) h/m c) h/nr2cl
e) hi n"2
c)IXYZI *
b)IxYZI : L2 T-¡
ffit..'-zrz
Planck; doncie p,
] ,,.', '. Considerando que la
hf, entonces.la cantidad que tiene dimensiones de iiempo,
IXYZI= tr
N4ti 2r
expresión de un proceso físico. Hallar las dimensiones de D y
A = Aceleración
B = Velocidad
F = Fueza
0 ,- Ángulo
a) tDl =, [Y] * Y-r ¡z b) tDI = M = MrL
c)[D] = tYI = M d) tDl.= IYl = M'r
e)tDl=[Y]=M'
PnOBLf,i[ANEO:22
Hallar las dimensiones de x en el sistema intemacional y en r¡n
sistema donde las magnitr,rdes fundamentales son longitud, fuerza y
tiempo.
1. ^.mPsec'(0.+0)-=
p
Donde:
oy0sonángulos
m =" Masa
P = Presión
p = Canüdad de movimiento
a)[x]=Y¡ry¡ b) txl = ML"fl c) [x] =ML''r't
d) [x] = ¡4¡s1t e) [x] ,= ¡vt¡-]fl
PtOBIAilA NfO: 2il
Calcular la ecuación dimensional de "x", en un s¡stema &rde las
magnitudes fundamentales son L, F, T {Longitud, fuena y tiranrpo},
Donde M = Masa
; son
hdi
a) [xl = F2 L3 T6
d) [xl * F3 L3 T-¡
b)o=1 c) c=1
b) [x] *" F3LiT6 c] [x] = f3¡s
e) [xl : F3 L3 T'¡
PR{)BL[I|ANB0: l5
El volumen de un cuerpo varía en función
expresión: V ,, Atr t'9 , dondg.-iles el
t .,g¡*'.
y V es el volumen
"n,
n#'trál" .
dimensionalmente conffi determine lqg,ii:i
constantes físicas A y E- Lspectivamente. .¡$.=
a) L2 T'3 y L3 T .;i"Et) L. T, y L3 T d
d) L T-3 y L2 T .1"i1_e) L3 Tr y L2 T .
L3T
Donde:
. p - presión
m i: masa
q " carga eléchica
w = velocidad angular
Cdcul¡rlas unidades de a I s en el S.l
Pf,OlLtlIANf,O: l7
Rpto:Kg A
Enconhar el valor apropiado de x que permite que la siguiente
expresión, sea dimensionalmente correcta:
t
n., jI *-
x
Donde:
I = m2Kg
alx= 1
d)x=2.1
; w =, rad/s ; K.- energía
b) x."2 c) x=3
e) x -- 2.2
$i Ttencs et PotcnclalilMat fe @rimde.*f](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-10-320.jpg)
![/*
r!r1:ii t j:.'¿,tl . ,i: 'lutt..r. ._4.¡_,
i,i
ACADEMIA GALILEO
.i,t
' 'l:l'
!:i¡.{f llEtiff ;5,Ñ}r{}: ?,,{.
I.n trn rjel.et¡nirxri:it.¡ -is,. ,r,it tjp rln,titultrs l.r. ;t" l))drlnilt:(le-
tun{iffi¡lsi.'hiriir. la veloiiiclacl <ie l¡: luz ,c llx 103 nr/s, Ia
."n¡f,áhif'¿1" Planck h 6.63 x i0sa Js v la mastr del protón
. nu{.S7x 10''7 Kg
' ili!'qué rnanera deben combinarse estas magnitudes para que
fomren una ma¡¡nitud que t€nga dimensión de lon¡¡itud?
Plt0ltUlllit ñIl()¡ 2i¡
l:» un choque se cumple la siguiente ecuación:
(y, .r)-
2
r. .---
1i Jlr,(1, t tn,(.,?,
donde:
p ,' Oanlidad de rnovimient<¡ line¿rl
O , Vekrcidad de l¿i luz
nr Mastr del cutltpt>.
Pn(lBI,IiMA Nn(h 2f)
I--n un experimento de labor¿rlorio se determina que un sistema
físico almacena energía I:., proveniente de una fuente calorífica en
función de cierta variable u: t: I: (a). El gráfico E versus c¿ es
una recta cuya pendienl.e liene las mismas dimensiones que [a
conslanle de Hooke.
Hallar la dimcnsi.n a" Jl
,,tl Jl1= I. u I Já l-= ¿-' L'- _t -' L' _t
'r [Jo-].. r ar
[Já f
= r
alJáf=,r
PEOBLüilA NBO: ll0
La tuerza magnética "F" sobre una car§¡a móvil q, en presencia de
un campo magnético "[1", se expresa por la s(¡uierúe ecumkSn:
l,',.,qvBsmQ
¿,Cuát es la ecuación dimensional de la inducción magnéüca "B'?
a
lBl,-Mr't" b)
[/]l., M'f-'ta
d lBl = Mr'r' d)
l,n,,
, u'r'f
et l9l- tu{r 1r'
., , l
.irl' :.,,
pd*fil**o: rr
X#:-Güuc.i¿n.m#Ética iBf producida por un conductor infinito
:e..,Q;****"]ffi l¡i' a
;a
H''
o viene dada por:
' i. :
t:tfll,f=lur""n
t#Pt en el S.l. de la pemiéabilidad magnética del
vacío..u¡¡. . ..
'' 'r...
Kg'tii Kg m Kg m .'
, a) ----;--:- b) , -
c) ---;-:-;.
S,A, S.'7, s_,4:
'Kqmr. ll i.
u) --;--
s'A'
Kgm
e) ...
s'A-'
,j:
PI0LI|E4:üI{F :}P,r
ta g$,iesí siUpuiite'*s dimensionalmente correcta:
.U:
t.'l
a)c¡h
di clhmi
b) c
2
h mr c) c'l ¡¡ ¡¡-z
e) c2 h m-l
" m.m-
Y (l K) '-mr lm.
Donde:
t/ va -vt
:..: .-.-_-- , mt y IIl2 soñ masas 9 vt, vZ, v'1, v'2 Son
v, -- V:
vekrcitiades
.3r""
ll¿rll¿rr lrr ecu¿¡ckin clirnensional rle v y su unidad dg'rrfehidu nn
"l ¿
: .r
, S.1. ,lt":
ti',:::
íf -,-
¿r) lyl MI-2'1 2 y se rnide en.l 'j ,;' ui . r
b) [yl Ml..'?T y se micle en J "
',]
Í..
^d"a'-c) lyl -, ML2{ t y so mide en J ,r'"' '..''li:.., 'r,; ,.f , l
cl) [y1 ,, , ML'21'2 y se mide en J "{ t + ,i..,:
e) lyl ML1 y se micle en J .1 "-r,...
'.,"
PBOBLIjMll ñll0: 2$ "' .....,.' '
il". '
l.¿r lec¡rí¿¡ n<¡s indic¿r que cuanclo un cuerP;p se rnüeve. con
vclor:id¿¡des cercanas a la luz, su ene4Jía está dacla'pór: ', .
l.(irál debe ser rul valor de x para.,"qüe la ecu#n se$,
rlimension¿rlmenl e correcta?
a) x 5
d) * 4
b) x,,3
<:.x'2
'-)rN = 1
' 1.: : .;
Pn(ltlillilrl Nlt0: 27 : r"li¡á,:":.:
l)elerrnine una frirnul¿r que nos permita expre§arr el vffii-ii'de
.rftua por unklad <ie tiempo (Q), de.nomina.do¡gásto Cüer#to¡ u¡
i.rg¡ujero s;rbienclo que depende de: ,'.. . -..,
volLnil.tl
I) ,', l)iámetro del orifick¡
1,,
-l
l''trcri:a
l) .- .---:-.-. l)resion
Areo 1..,,t
c . (lonst¿¡nte adimensional :..,t.
Plt0lll,Dllil NBO: 2ll
L¿r velocidad V <le una pi:rtícula de rnasa m c¡n función de tiempo
L est,r dixla pr-rr:
r. 2nt ltrr so. f 1T, , .l(i , j ) m/s
I l* 'l
I l¿rllar l¿¡s dimensiones de lltl, si [o es una tonaiitud.
pq¡tde.lYln mide en mehos. Detennine [a ecuación dimensional de
,I ... l':.¡'.;t,.'i' "'
' ..1.:,i'?'
y ,*+!1+ I
mn
u)
[abcl = L'
d)
[abc]== L'
'Hl-.^,rt,
o) IKl,Mr]
llrl
")
lKl't-l
': i. I Il I
ti..lKc) I--.
I 11
M'I'-I
MT*'2
M1',3
En la siguiente ecuación homogénea:
Acos0
M=ffi"b'l
Donde:
P '' Presión.
. b = Longitud.
M =', Masa.
Determine la ecuación dimensional de K y A
a) L y M'LT-'
b) L y v'Ll-'
c) L y M-=LT-'
d) L y pt'r-t-'
e) L y v'LT'
e)
K
il
flbíeanas m fs Av; lle l* &tltsm1076'(frente a la ÜNSAAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-11-320.jpg)
![t-
I
Acadermi*. ü's
-Íx na¿l¿
PITOBLI]IA Nll0: l],1
¿;;i;;;; ;i";tJn irg*.o per¡:entticularmente a un campo
magnélicr> uniforme. describe una circunlerencia de radk¡ R. I-a
ecuaci<'.¡n que calcula el radio de giro depende de la masa del
electrón (m), de su car5¡;r eléctrica (q), de ta velocidad (v) y de la
irrducción mag¡nética (B). I-a fórmula empírica que describe dicha
ecuación cs:
K: Constanle numérica.
u) n,.«Il-
qB
.) rr ,rlllq
") n ,rlLY
qB
PROlllBlIA NB0: il5
I-a potencia utilizada por una t¡omba centrífuga para elevar una
cantidad de líquido hasta cierta altura, deperide del peso específico
del líquidr.r (y), del caudal efectivo (Q: en m3/s) y de la altura efectiva
(tl) a la cual se eleva el tíquido. i,(luál es la fórmula empírica de la
polerrci,r?
K: C<¡nstante numéric¿¡.
a¡ P: KyQ b)
c) P. KYQ/H d)
"¡
P=I§H
Ptl(}BLIl¡UÁ rlt(l: :l{i
[.a velocidad cu¿rdr¿itica media de las moléculas de trn qas depende
de [a lemperatur¿r absoluta ('f), de Ia masa mola¡ (M: Kfy'mol) y de
la cc¡nst¿¡nte universal de k>s gases (R: J/mol'K). I-a fí¡auüS empírica.,,
p;rrar dichii veloci<lad será
K: (lonstante numéric¿r.
Pn0BLnilA Nlt(): ilf)
lt?
I'lallar la ecuación dimensional de ¡:-. si se sabe que
a
( ,, ,
x - I rn(ut)te[u,'f--''t,J
bi n '" rILP-
qv
d) n,, r--LmqB
Donde:
A -. longitud
t.,= tiempo
A) LT.
d) Lr-'
Donde:
a "-", aceleración
=..Ír¡,l',:.;
m::i masa ..i:t :r:i.:. .r::::ii
P -, potencej,' ,.i:.i-'
w',.velocid᧠angufár
GR.UPO GALIL§O
C) LT,
ti,ene la
b) LT'
e) L'l-'
' l.¡.,
PE0BLEilANR0:4O <. .' :'""-.
Si la ecuación siguienle es dimen§ibnalmente corifrh
9,:á = u*rpu.
"JiBi
li .. ..rü'
L$iiller¡*"*, ,1¡;¡r
,iir{ijk;i+;iiir l¡r"
P ,KyQI'I
r,. z(ryqu)
<presióE$$e,n?á es dimensi<¡nalmente homogénea.
I ex)
Al, Vl logKrer I
't)
a) .. /nr'n'. ^v-r'
..' , = *JH
,,
"..,./nin
r,i1ri:L i ir{l l;
Dond8l;iilli,i'
A,=,á a
V---"velocidad
:¡¡.,,f=, 1¡srnp6
b) u -- K.lU_lM
ar
": rU[J]*-
., :: . itÉi:!:j .
tii.,;árrlli¡r:I;. lri:r '"r riiriiI ii,:::
,il*'L ttitit:.1::¡".
::.:. . j tti.f!t,_
tl :ii,rsniii!1:':r'i':,
"i.::.::r:
l:1' ::jiil) i¡
(luá[ es ia ecu;rci<'rn dime.nsional del trabajo en un nuqvo,sisterna de
unidades clonde ias ma§nitucies fundamgg.lt-átes r"" i-'á a (p),
vek>cidad (v) y lrecuencia (f ). . ,,,.1 .. .: i.
.) lwl pf 'r'' j "',#ii:.
b)
[w]' pr'"c,, :!!'
a,:l r
") [w] "'pf'v'l'il
.t)
[w]"' pf-3v-si'i
") [w]='' pf-'vs
Plt0ll¡,li,uA NR(l: :]ll
Delermine las dimensiones de X en un sistema de unidades cuyas
rniignitudes fundamentales sr¡n: área (A), energía (E) V periodd {T).
-
3"- ,{vt + R)sntro"
m tg60"
$i:
m fnasa
v.. volumen
h .,,, altura
o)
lxl=t,t'' tl lxI l, Ir
.) lx I ,,tt't' ' a)
Ix l-,sr'
"l l*l Ii l'
i:tr;i::i;i.ii
#*$lállar [a ecuación dimensional de "X"
F.) [x I = t_r-2 b)
[x 1.,, l.r',
") [x]= I'r' d)
[x 1.. lr '
") lxl= ¡.'l''
PIlOBIJillA NBO¡ 42
En la ecuación dimensionalmente correcta:
o ' ]lQrls-j!D'
E2
Donde:
A * fueza
B ,:. ¡¡¿5¿
Q * profundidad
D -. densidad
E.- tiempo
Calcular el valor de X lY , Z
a) X1-Y-tZ - I b) X-tY+2.,,2
c)X+Y + 7,, 3 d) x t Y +7..,3o
e) X r-Y tZ,'12
PII0BLIIUA NBll: 43
Si las unidades de E ror sog¡undns. áQuá unidpdes
m4nitud que mide B en el5.I,?
, =,po:-4i:Ü ,, ) d,''-
l 8, r Il1 t P.t | ...t 1,"
u !f,-,JTJ',
Donde:
Ae'"5n mehos
Ps-'27(coso m/s2
ltptn: m/s
i.Tíi mén€§ d.Fo*nsiqL.¡üaeoAloa la §xpsriv*eia.."l](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-12-320.jpg)
![pris¡c.*'x
t-,,*ffii ,'AytB)r' y-' r c
t:s homogánea.
ACADEMIA G
PBOIlLltrlIA Nlt0: 5()
En [a ecuación dirnensio¡ralmente correcta:
AXr r BX *¡. l_l§_g:1"
Si: V: velocidad
Determine la ecuación dimensional de XC.
Hatlár la expresión dimensional de C en función de las dimensiones
de ts.
neta:[c], IB]'
Plt0BLIlllA NII(I: 4ñ
Determine las dimensiones que debe tener C si la siguiente ecuación
es homogénea:
bltxcl
JT
olt,ol-ilf ")lr,i=rFt
(o'+ n)' Aser,1o'
7fsen0
B
¡¡,1gsen30'
('=
---A
u)
[c]= r--'r
c)
¡6'1= r'r'
l,lt0tll[trtll NRO: 46
torque, viene dado Por:
Pll0RIJilIll Nll0: 5l
En la siguiente ecuación homogénea:
JA + Ill' + A(''* ::- [3'2senro
Calcular el valor de "n"
a)n*,-2 b) n,,,3
e) n ''' -3
c) n 1
El ángulo de torsión de un árbol cie sección.,.qirculur,*qodütdo a un
PB0BLIIIIA NR0: l¡2
Si la ecuación siguiente es di¡nensi<¡nalemnte correcta
. atrl !
Pbce
h''
2Sen (wf! )
Ilpnde ;,,,1,.,
',,, .i.'
a: acel&ácién.
P:foterrcia -
- rii. ed
.i: .i:.
l:
TI §
Gl :;;ir:, ¡|" ,j
l'
Si el periodo de rev<¡lución'f de un satélite alrededor
depende del radio R de su trayectoria oilcular, de la '
.) r-KJuts- d) r=-,Fi' '
") r -, KIE
PI0BLI]IIA Nf,0: 4B
La energía por unidad de volumen que kansporta una onda que sgr'.
propaga en una varilla está dada por la ecuación:
P '' I /2P"wF¡t' ' ,
Donde:
¡rlr
"'{1,, ,
' p - densidad de [a varilla.
W = frecuencia angular de oscilación.
A = amplitud de oscilación.
Hallare[rralordqtr + I - 2Y.
a)o "1-
P-2r= g Uicr:0-27= 3
c)cr+§-3Y= t dla+ B-&"5
e)o+0-&='-1
: jir,r:
PNOBITilAI|llft ¿O
Si la ecuaeién nro¡bada es hornogénea
a"X+an*lX2 +an-?X3 *...*aXn = K
Donde:
a = acelemción
K = constante física
Hallar las dimensiones de X.
u)
[xl=. lr-' b)
[x]= lr'
,,)Ixl..rjr" a)
[X]=lr' ") [Xl'.'L
tlbiícanos en Ia Av. De lo Culturq1076 (I¡vlnte a la UNSAAC)
[x ]= tvt t- '
,¡}
x = fuerza ..t:'"..i;rr, ,1i,,
PnoBl.rni'irxi} l$ i "
Detennine4fás]dimen$ónes de x, en un sistema de unidades cuyas
magaffiáE§:fl¡nil4*¿;*,nt ron, Ár"., energía v perío<io'1"
-_.1L-: ,(vh r R¡s",ro"
.;nr' m tg60"
rd.l1. tltása ,,. ,-;, i :
.*r¡f-U.ia.a ungt iui ,-:'
.r;,'.
_-,-t*
i$g1é ","süiüa*q$"
representa x?
:r. . +t ,.,:.
Wtx l= M Lr-'z1: u) [x l = M r.r-'
tr:n
'r;;x = fuerzS x =, fuerza
. d [x]= Ml.r' ,t) lxl". MI-'r-'
f *=fterza x.=fuerza
Si;,,i .r.i_.r"
. '. t$:,'masa
. ,,.,
'volúmen
.,oli,'h,ulturu
d [x] = ET3
") [X] = ET-l
") lxl = ET't
b) lxl = E7*-2
d [xl = E't'1
PBOBLf,üAlif,ro:5{
A partir de la exp'resión mostrada y d es dimensionalemente
correcta, detemrinp l¡r dirnensiones d€ S y Q respectivamente'
[; ff;-i) o
I Y E,)
Si: A es área
a)Ú
d) Ln
yL'
yL
bll- y [."
e) Li, y t
gravitación universal G y de la masa M de la tiiz"ga'
Determine una expresión para'l si." r.U-?",qiid'. L
") ,-*J-jn- b) r-KuE i
c) Ü y L](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-13-320.jpg)
![-
1t.
Pll()tll.lj]l¡t NIBI]: iri
Iln la ¡necánica cuániic¿l (efccto compt<¡n) se usa lar ecuaciórr
h: constante de plank
tIl¡: IndSó
)", 1,, : I.ongitud de on<la
v: velocidad
c: vebcidad de la luz.
") [], l ML''f -'
t')[hl,Ml''l'r : ]
.) [h I Mr.r'l'2
d)
[h I vl t. "'r
") [hI,Mr.'r ':
f
'lt{lllt,liMil NII(}: i-r(i
I -¿r fuerza con que un chorro de agua presiona una pared depende
rlei diárnetro del tubo(D), de la velocidad v del chorro y de,,.:ltrr
densid¿rd p del líquido. Si cuando D, v y p tienen un vá@
unil¿¡rio en el S.l. la fueza aplicada es rl4. Detenniire la fórmü1á
quru rel;iciona dicha fueza.
¡) r, ?.1
p D
,v,
,;) r. 1) o»,v,
e) I
ffi'*utl*mry;*§W: G}TUPO GALILEO
I" t
vA r JK t/cVcV....o
Donde:
e: espacio
v: velocidad
l-u l-tr l-il
.) lr l- ¡;-r'1' b)
[A I ¡.,i ]r c)
[a 1
. ¡;r1
I +n :-n
d)
lnl-.L;r e)
l¡l ¡.;-i.¡'
PA0$Lf,itANf,0: (l0
Si la siguiente ecuación es homogénea, hallar l¿rs dimensiones de X
l,Rr/Sencr ,.f / -.,--
VXt/XVX.,.oo ',,,.,l" FSeC0 ,;;,',t',,i,,t1r.:;;,.ffiirit
Donde: ,t,
p _ presión .. ;m:: masa ,:
L - longitud ..t1,r0"
r- :ruerza.
Aclemás se cumple: 42Rmien:0" + B? = F
,..u) [xl=. (*t,)''" bl,[x].- (*,:)"'
5$f"l =Qrr)' ' ,!tlxl,-(uL')'.
E1x1-1,rzr)'""',: -..'
Si en vez se considera a la fueza F como magmnitud
determine la ecuación dimensional de la
[Cl= r'-'r'1:21-z b)
[c]= F-rL-rT-2I2
dI [c]: F-rL-rT2I2.) [c]= F-rr2T2I2
") [c]= F'L-'T2I'
Nnlh G2
Hallar las dimensiones de Y, sabiendo que la ecuación es
dimensionalmente correcta:
Y =" X Pe3xmr
P = Potencia
e = Espacio
m : Masa
t = Tiempo
a [yJ - LsT-o
"l [v]= L'Tn
.) [v].. r-'1-'
PilIf,I.fTAilf,& ü} -
Dada la fórmula homogénea:
K=Af2+A-'W'
Donde:
f *- Frecuencia
W= Energía
Determine la unidad de [a magnitud K.
.) [K]= ML,T-'(watt)
b) [K]= MI-2T-3(watt)
") [KJ'=ML'2T-3(watt)
d)
[K]= ML,T2(watt)
") [K]
-., ML-'T-3 (watt)
¡T{t TiS.¡tg§,elfqlen9ifll.. NgÍotros la Experiencio.,,!
.lrc,tL.,-.l, ,., I)'
''*"[J'(')' )
Ptt0!¡Lllllrl NltO: ñ7 ;'
l.,r ,:nlro¡:ia S.s una magnihrd física esca§jfu,
iir¿nlro de un recipíente aistad-Oi¡i¡ ido realiza ffi
rr¡r volúmen ir-ricial V6, hasjaffiüolúrnen final
_!ite
AS rrll lnlv lv.l' r .{,r r.
Si: iü .,:::,::;:i,1,Íi:,.,,.
lr: ltúmero de moles, ,.'- tt:.;Í".#li
Il: Cle. (Jniversal dáhs gases. -T,],:
i .l I i... ¡;
I r --- ''-"- | 'ltid: !)a
I nrol 'K i ,;r! , r"
l..r- n-
l)etennine lad untiiffide S en el $éma intemacional de
unidacles. l..t'F',,.' f-
?'ii{t.:r:.:-::':'::: npta: J/gK
b) F'.., ApD,v,+1
d) F " ipo'u'
b)
R"=K!-Y:
p.
d)
*"-*o-Yp
ul [v ] '= [.'T -'
al [vl= ¡-t1-r
PttORLIIMll Nf,(l: 5ll
I.-.n la dinámica de fluidos existe una cantidad adimensional llamada
núrnerr¡ de Reynolds; la cual depende del diámeho de la tubería de
conducción(D) de la velocidad del fluído(v) y de la viscocidad
cinemática (p). Si p tiene unidades m2ls. l-a fórmula empírica del
número de Reynolds será:
u)
n... i DY
p'
") *",. *-P,'
l.
e) Ite , ¡1 -{.-
DV'.
PII0|]LBIIA Nf,O: 5f)
Si la siguiente ecuación es
ecuación dimensional de A.
dimensionalemnt€ conecta, hallar la](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-14-320.jpg)
![p-isxcg" x ACADPMIA GALILE§
Plt{)Bllllllrt Nlt{}: {i,t
l:-n la si1¡riente fiinnt¡la Iísit:¡¡:
Dw2X'V Ñrn-rt hlg¡lr
I)ontie:
x. lr : l.on-<lilrttles
l) : l)ensiciari
v :Volumert
nl : M¿s;.r
g : Ace,leia:ión de (lravedad
w : lrrr¿cuenci¿l ttngulzlr
l)eten¡iutr a qué mn5¡niiud representa trr/R.
^l [nlnl l]rr t)[A/Bl. l,'l'-] .)IA/81,, til'1 |
d)
[A/t]l l..r-r e)
[arnl ,. I)-)
PBOI¡IIiMA Nlt(l: (;5
Oalcular (a t tr) elr la si1¡uienle ccuacitin homogrinea:
, a'l
Jn -1 (scn-30)1"'r rwh-l
I
l)<¡nde:
[:: I:t¡en¿l
W:
'l'rat¡aj<¡
h: Altura
h) a t b 3
d) a t b 2
Ptt(llll.lillA ñ11(l: (i(i
L.a expresión: sen ( xv 2 I I:l- L:)
es <iimensir¡nalnleille c()rre(:l¿t.
Donde:
li . I:nergía
v Velocidad
l; I:uer¿¿¡
L. l)isl.ancia
áA que rnaJ¡nitrid l:ísica'represertta x?
Ptt0nLDilA NIl0: Gs
Ll torque en un acoplamiento hidráulico (r) varÍa con las
revoluciones por minuto del eje de entrada (N), la densidad del
aceite hklráulico (¡:) y el diárnetro del acoplamiento (D). detemine
una expresiírn para el cálculo del torque.
a) t .. KNr pDs b) r ,, KIf ptJp c) r = Kl,l¿ pff
d) r .'. KN3 pl)1 e) r -. Ktf pf)s
Pn0BllltrtA Nll0¡ 70
En la siguiente ecuación homogénea:
/ Vl E'
-
V) + 3El? x'yz
V -' ()--;f -- - znr* " s*
Determine las unidades de
si V cs volumen.
a) L12
d) L'§
b) L2o
e) L16
c) Lr7
b) [Al= r-, ; [sl= L,
d)
IAI .,r, [sl= ¡-
b) a tb' 4
e) a t b .3
c)"rl'+:ti:;::
' t', _, ''
"' ir
b)
[a] Mr/rl'r/2
,t)
[Q] ' M2/rT':]¡l
)r
lxl "M
a) t-
d)Mr,
Pft(lllllltlÁ NR(l: li7
l)elermine l¿rs dimensionr¿s de Q para que lae,§igge4tes
sean dirnension¿rlmenl¡: «rrre.<1.zts: . .,.t
W 0.5nrV''tl' t Aglr r lll'}
Q.^"Bl'' ' .,',.
I)onde: ir
W :
-t'riütrjo ,,'r'
m: M¿ls¿r
1 :'l'iempo
r¡ : Aceier;ickitr de la 1¡rttved;rtl
h : Altura
P : Pdenci¿i
") Ial M-rr'r'l''1rl
.) IQ I Ii{ 2¡r'l'r' l
,) [al: ¡u1tir'¡'t'r
l'ROIl[Il]IA NIl0: (il]
Si existe un sistema de unidades donde krs mag¡nitudes
fundar¡rent¿rles son I¿¡ velocidad v, [a fuerza F y e[ área A. Hallar la
ecuaciírn dimensi<¡n¿rl de la aceleración en dicho sistema.
o) lal,
- VrA'
I '?
t) [af =VA
r'?
i
.r lul v'A' '
a) [a]=,V3A "r ,, l . l '
") [a]
.= v'A' '
Q,,,A'
a¡:¡4¡;i-"', [n]= r-
6j=r, ; [Bl'=r-'
.) IAI= r -'z [n]= I
Pf,llBl,f,Il$Nn0: 7ll
Si la ecuación :
mv2tg(wy- o¡ '. {
Es dimenslonalmente correcta. Calcular las dimensiones de X, Y, si:
m ,,. Masa
v ,. Velocidad
W .- Velocidad angular
"l [x]- M2L4 lYl-'r
b)
[xl.- n,t'l'. [v]= r
") [x|,,*z¡ [vl t'
d)
lx]. rra'ü [vl* t'
e)
[x]- r, '¡-.' [vl='l'
I
b)1' ' c)M
e) Ml-1'
Si: .,."; :
w =-;dáiáio' '':
m-,::1táíár .,,.,.'
Si-. Ardá' " ''.-
¡ -:-t
UbícunosenlaAv.,Detd'.aüIfu:raI0f6-(fientea.toUNS:MC)-](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-15-320.jpg)
![I
ffiAcarle.rnig W_ GRUPO GALILGO
PB(}BLEiltA Nllll: 7f)
Determinar una expresión que relacione la presión P de un fluido
con su densidad p y la velociclad de movimiento del mismo v.
a) P = Kpvz b) p=Kpv' c) p-Kpv
d) p = Kpv-' e) p -- Kpv-j
PBOII.EIIA NN& 8fl
Se ha inventado un nuevo sistema de unidades, en la que se han
elegido como magnitudes fundamentales a la presión, densidad y
tiempo (P, p, t). en dicho sistema la fuerza estará exp,resado por:
a [r]=.r'o'r.' b)
[F}..
p-,D-rTz .] [Fl=p-'» 'r'
d)
[F] , P,D-.T2 ") [Fl..P'D'l''
?ilorr§raNfo: sr .+,r#;á;#Áffi*
Si la ecuación dada es homogéneg¡ffiHiüiáirtffi-ae g.
... :
._:f ..
-_---
.','"
I ___ "b4¡,
¡4tm'e-w', -r/l' r-JBsenx 1V-r M ¡Z*8 ,.li
M = Masa
a)0=6O0
d) g .- 46o
I}ROI}I,II}IA NIT(}: ?4
IJrr fenrinreno físico r,lst¿i regi<1o por la ecuación:
X Ae atsen(bt t'c)
Si X está medido en metros. t en se¡¡undos y c en radianes,
e .2.71 ... itrláles son l¿rs unidades de A, a, y b?
a) m.s'ysr b) m-s'u.'' c) m.stys-'
,l) m,s' y s' ") m,sl y s-l
PIOür.Enn ñnah 75
Calcular las dirnensiones de A;
I rl
n wlnr l,l:l
L P. 2sl
I)<¡nde:
W,' Peso.
Pe l)as<¡ específico.
h ,- Altura.
P ,', Presión
a)
[R J
-. rvl l,t,
d)lnl=-uljr*'
PII{}BLII}IA NRO: 7G
(l¿rlcular la ecu¿¡ción dimensional de R en la siguiente ecuación
hornoqént:a:
A1 uA2son áreax.
g,. Aceler¿rción de la ¡¡avedad.
h',, Allura.
ul [n].,,t.''t'-'
¿)
[Rl.,lir''
b)
[nl-. n¿1.r, "] [AI=rufr-2
") [nl,- rr,lr''l'
'tt'i-b) e ..130"i{b,. l 1a¡;!,.}i,,$r
P):&,=50" .' i1.'.,,:¡i¡;:lro
PNOBI,DIIA NN(h 82
Determine hs &rensiories del producto de las magnitudes c y P cn
la siguiente ecuación homo¡¡én-ea:
:::',. '=.,, P uw2x2cr#(wt)..t pBxf
Si: ,
I -.,.-ii--
¡t . A, l- ::-
',1,!-r' r
{Ar
P:=,Po.topcia
1,ti¿Ei
a) P=kpaÉ
d) P=kprftt
;'I .: r.i,.,:distancia
; p"-"densidad
b)P."kprÉÉ
e)P=kp#f
,
.:.:;::ii:=!€1
r.j
*=) topl.=t"tt-3ti'É-i;+ ) [oBl="uL-tT'z
liiiiii*rigPl..l¿lt'¡ 'z" d) tertsl=,MtJT
I
i#tffi.s.*,Jtl*1.*
PR(ffi'ilno: a:l
F-n unrlir', uevo sistema de unidades donde las magnihrrdar
fund;r4.Étentales son el volumen, la presión y .la acekreción;
!¡""§elgtrnine la ecumión dimensional de la potencia en éste aist¿ma.
Í¡ii?i,t#IPoJ="v56P a-2r b) [Po],,,vr6P a-r2
';ii:i:j1:11 rn-.r rfl6ñ ^r¡3 i rñ-r r rslfrn -t2tr"liié)
[po]-,Vurup aa3 d) [po],..yvep uta
iri' e) [po],,,Vr6p ar/3
PROBLETIIÁ Ntr(l: 77 ,,..:.j:i,.
I :rr la siguienle ecuación .h<¡mogénea, determin"r. J4§ii;, : :
si: '...,,.-,*.,*
e . (panr() i, .- {J+ffiF;":,5
ür metr() . ..:. ii:l _ xrE¡;J' '
o 45" .'' , ii
e 2,1|... .' -,,,.-".,.,-,
s.segundo. : .a;irl:.'
{ ^, ' ,, 'r n,
X I Rr' "' -rqu+5*'5.-(log20)(sena)sl.' jeii,,.,
I nt/ s nl ..lr1?'"+;
' ¡+rii;-'
b)[ABI, L')
"¡'1,¡
[nn].-rr .] [-ffi-L'
¿)lrull,,¡;, '.ir1,tr4e1,,,11
"-,,4
..
.. ' tl'al'
pnoBLDüa Nno: 7dt ffi ffi:ltti'ii|i, #+
l-a presión sonora de uná"dffi.&i{óttiene a partir de una constante
R que se determina por:
R "'----v-*--.t/k".v/A
Donde :
' t ",'tiempo.
V .', Volumen de la sala
A' Área
r.Ou¿iles son l¿rs uni<lades de K en el S.l.?
a) sur
1
d) sm
b) §Tll c) Sl11
'1
e) Sfll-l
v,,,vel& ll r
PBOBT.BIIA ITTft 84
La velocidad de un satélite artificial terres&€ que ee de$aa
alrededor de [a tiena depende de la clistancia al centro de ta tiena y
de la aceleración de la g¡ravedad terrestre. Determirie la fórmula
fÍsica que permita c¿¡lcular el valor de la velocidad.
") v,.2kJG b) v ,kJRc/2 c) v=lfiRs
d) v.-krfiG
"lv'-3kJG
Pf,OllLf,llA lllf,O: 8B
I-a potencia con que se aplica una inyeceión depende dc la
densidad del líquido encerrado, de [a vclocidad del émbolo para
expulsar el líquido y dcl tiempo de aplicaeón de la inyección.
Determine la fórmula fí¡ica pam la potencia.
t ) [R]. üT-rcl [n]=
o)
lR],,,I-'t''
c) P=kpvtÉ
Pl0ll§.lilI0: BS
Hallar las dimensiones de "C" para que Ia oiguiente ecuación sea
dimensional¡nente corecta.
C=ABPAFervrr
Donde:
p ": potencra,
e = espacio,
t = tiempo,
F = fueza,
m = lTM§a.
a)[C¡-¡4¡--z b)tC]=MLl
d) tCl,..ML4 e) [C]..¡4¡-s
c) [C]=ML2
¡Tú Ttenes et Potencial Nosatras la Experiencia.,.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-16-320.jpg)
![Fr-'
3'I
Plt0ll[$llA NR0: ll7 .. .
"., ' .,,
En la siguiente ecuación homogénea. cletermine e[ valor de 0
W csce
= m.c
cos e
Donde:
W'=en¿rgía.
C,,..velocidad de la luz
mi:masa
a) 0,..30'
d) 0=50"
Ptll)llllirllrl NRO: Bl]
Hallar Ia ecuación dimensional de "a" si la siguiente éxpresión es
hornogénea.
ase')30"+b4cFsena = C
r' ttt ' :'; '
ACADEMIA GALILEO
Determine la ecuación dimensitnalmente de
a){El=Tr b) tEl*T-l c) [E]=T3
d) IEI=T'ze) [El-l z
PItOtlLIilLt Nlt(]: f)I
E,n[asiguienteecuacióndimensionalmentecórrecta:
t-
Ke¡r'| *n{
= rl A*" +r[7 sena + K +ü
donde: K,A y 1", son cantidades físicas. Calcular el valor de $.
a) 0=2" b) O=o' c) Ó-1"
h
t;- -
ac
b) e=.i0' c) 0".40"
e) 0,,.80"
d) O=e" e) 0=5
PROlll,IiMA NttO: 92
La ecuación dada es homogénea:
IAB+CD1"""to" =.lDA-! r
Si se sabe que:
p = presión,
'D
= ifiinsidad. .,
"t]Í.1.$f.,.| stdtrs$ de "B',-
a) [X]=L3
b)txl".L-1
c) [Xl=L-'z
d)[X]=L'z
e) [X]=L1
lql+I;'zJr i
1Bl=l_'zfr á ¡n1-¡-'t1''
dettsidad'py üolqpidad v choca contra un
PII0BLEI|ANRO: $(l ,
Se da [a siguiente ecuación dimensionaltonecta'
,, 3o , (h -b)v
--f
tl'
Siendo: :. l
V = volumen
i.. tiempo.
h .= aliura.
'[as
magnitudés Físicas vectoriales.
a/ v.J
,, orl
5y ",,,,
^tVil¡'"
-']' /
"rY *r,^ APunto de Aplicación.- Está <i¿¡do por el origen del vector.
Intensidad, Módulo o Magnitud.- Es el valor del vector, y generalmente, esta da§o en"escala; ejemplo
'.^
Sentido.- Es la orientación del vector.
o)
llbícanos en la Av, De la CulturaT@7'6 (fren:É'd la ÜNSAAC)
10 m, 15 N.](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-17-320.jpg)
![r
-f< A l/edor A
COMPONE,NTES RECTANGUIARES:
"t A.* ACos 0
-)
Módulo delvecbr A:
t
A =lA*;A.r; A-)
{* AMófulo rtel vector)
o 4 ,,,ASen9
GNÁFICOS PARA SUIIIAR VECTORES:
A conet"j:,iT4' u.o o "n€.d
."rr'7-/ ,l efiufl 4 ,e
./ /_. ---.' dobrA =D id
GrtUP{} GALILÉO
dPreccioh farn bor
co mol¿vnb,íen oi.§o
Ac áer¡r¡c
4. Direcclón.- Está representada por la línea de acción del vectr¡r y el ángulo 0 que forma el vector
-
:-
I
I
I
I
(
¡
i
¡ = (Acos0;Asen0)
l'-- -; "' - "".l
[*r» -P -ol
1. uétodo d"l
R es máxirno cuando I y ,B fonnan un ansulo de O'(tt)
Ax
r.4ff
t,:i
..n
.i?,:
'tr:'
a.
b.
R es mínima cu,*rdr) y ii t".r". un anguü de 180"(t.t)
*,. am **¿rf, y É tor*u*unángutodego"
MODUI.O D[ IA RF]SULTANTH:
R fit' I/-n;Ñ
¡T4 Ticwqel ?otr¿rlqlü1.¡{osdrqs lÉ &p3r{ens¿4,.."r](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-18-320.jpg)
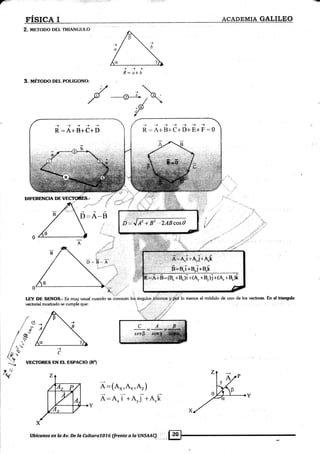
![Áü§*dffiÉa {3al*}w
Cosenos Directores.
* c.ora =Ax * coso -
AY * cosy =42-
A
-'--r
A
-' -' A
VECTOR.UNTTARIO
.^
Lrl -. j:(loscri+(losBi +Cos7kta
r
C¿ls-'u r (.os-'fl t (bs:y I
DosueeJorescualesquiero Á y li puerlerr *rrnatüpJi@aw
t) EscAIáRrilENrE.-
El producln escolor de das teúores ea ¡¡n nús¡oer:n r,€*1.
.§¿on lo.s uedoras:
A (Ar.AY,A.)
ii .- (l]", Il., Iiz )
A.li (A,Br I A'tJ' t hzt /) "
A.B=lnllr{co6)* "-§Ñ ro J t
t' 'il'-t' "' . +,
A Es et ángukt lormado por los uectores A y B.
2) WCTORIAI-IYIENTE.-
GR.UPO GALI'.€O
=(ArB, --ArB")l - (A*Bz - AzBx)f -r (rt"B, .- ArB.)f
Los uectores unitarios serón:
AxB
íxj*fi,
-i
.l xK =t
i:.a
&xt = J
',Ax Bi=,Ait$i sñ ar ¡ I lt I ,.
,:í''' l::! .-) ..} -) -+ -+ -)
Triptc p*oduc*o vecterial: Ax B x C " B( .4.C)
podueff;*eltleal:
, + i:{l}:l+*::!._ r ., . + + +
k¡ C ;:;¡i$:r;F¡:1$,§r,r$ .= C . A x B
-+ -) .-)
c{A.B)
dos v€ctores es
ffijei,:
(cos o' sen o)
Ail!¡--S,.lAlfeb. a, Cos [t, Cos 7]
Cuando dos tsectores Á y B se multiplírnn üeatorialmente -¡f
.su resulf¿¡d<¡ es otro uedor perpendíanlar ol pleíl:o liii
losuecloresAyB. 'l
.Seon lo.s oecfutres:
A=(A*,A",Ar) , B:(ll*,I1,lt) *
uectoríal se defíne así:
r'.i
fi
ri. +t.A
-)
A
-)
A
-)
A
-+
A
l;
ijk
Á*ñ I
A* AY nrh
I B* BY ÉryI*
;ii
q
JJ
y
'/,{*
.rl ,,"r,t'4
r
v ,/*
./o'*'
iF
Pf,OIII§üA Nf,O:
Determine e[ valor
diagonales cenhales de un
Pf,OBl,f,tA NBO: 03
Si el producto vectorial de
Ax B = 3 i * 6 ¡-r 2i ysusmódulosron4y J7
respectivamente, calcular el producto escalar de dichos vectores,
N247 U3"tD
r=
c) 3{5
»3J7 E)2",I5
PtOf,LEHA ñlRO: 04
Hallar el valor del ángulo 0, a partir del siguiente gráfico.
Al*u2
D) Í 1/5
B) t 1/4
E| 7. 716
9) t 1/3
á(.*-'(Pf,0Bl,tltA NIl0: 02'
En el conjunto de vectores mostrados, determine [a medida del
ángulo 0 para obtener la resultante máxima.
Y
'*Yy'q
/],
w#A) 20" B) 18" C) 15" D) 30" E) 60'
, ¡Tú Tignqs elPgtcggiql, Nosqtro$ lg Experiencia.'.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-20-320.jpg)
![r*
I pma¡.ru,tNn0: (t$
Si M y M' son puntos meriios «le AC y de AB I l-tlln,
e[ módulo de la resultante de los vectores que §€ mueskan en
AI3 28
" I ri *1,. zu , I
n
"o::tsiel
radio de la circunrerencia es de I cm'
AC',,ÍlOu
A)60" ts)30" c)37' | ^, ^t7
- ,lA'
*:ru-,'u":"u Ittt 4 ¡
l;;1 ,1,,-, ;,
o-'u I ,,f- /
:
^)5 "»
(.t2 | ¿ _/I))4 $"/' I n*u*r**anrf,0:,)
pBOIl,EuANROrroG
l?h . _t , [ u. ill':l
, módulo de [a resultante de los vectorós moshados en'ta
t:ntasiguientefil¡urarhátlarel mócluloa" Á* d : -Útn", {". ,il;," B'-3m. c='5m.
,i h,'ltl 1 uau/ 1",,i{,+'| 't"-/Ér /l /l ; i t / -l
'/.-.-l " /l
- r¡>-'''"' 4;"Y'' -l'"
/ N / t .,/1t-,, ,,1 e¡a,¡¡,,;, p-)6m * c)em.
// YlÉ,*rt I §áiffi ,:;rpíro'n :
.rl ZdY' I l}iallar el m6dublderla resultante de los vectores mostrados en la
,: '
,L# ' | 'ff1...*
'i!i"'a r{
I,;';,; ""'"'-*l'nrg1 .,,nr,z
".*n,
+- ;;,
»lz.'34'.loJsZ."rl';;;,-."l.-W%,,;"i
l]ll]i:]l^)":-.:,." m<i<ruk¡ ^[ü unidades;..."" ,['""
^ ttt{ Jr^")¡x:rlrcrrdicularakxvectores , |
" , .' 7¡l ' {¿
r zi 3:1 t2[rd=,'.'i"i*',j [, ]
| l]i8[.r-.,,.:.:]"Ei3gp
c)80p
^)2
¡' +1, r ( lrrnrrunÁ,Nno:r2
. +
- .- 4P^ I Fhllar 9l módulo de la resultante del conjunto de vectores que se
rrr 3ir2) JBk -r'ró
l*ys*enlafigura.
cr i zi qi t:o^ ':-rl
"o''
:l 'i ],-:, '7'%J6§['
e.=60"r') ir4ir2lr ) !
,1j
5¡r
i?J:Ttjit:Lfiffrh **** de hn wctdresmmtrados ,' n i'1. A)40,5p E)46'5p s)42'5P
i's,,'.
'l.iiáJ,;-il;#; d*es&{&e¡n" .t#f D)4s'5 E}¿a'sp
r Ív' " P pRoB,BrA Nnt» tl
( m r il ^t rb I nm'.;,fl*,#ft0;offi.lt"',úl'*.H,I:T,,Hf,
G,N.,.V;'lresukant€ M
§'" #'":/' I f-;-l
$n* t*ño ere,cm.
' T.AJ
I lt>,,--]*il)ü.l; Eíáér;r;
i".,oyo / 1 V -"-,rl ffi:R =r,^D
/ 4 r^;1
tú
Pf,lltLBllANBO: 0$
{xü{¿uraf n¡ !n{r. FGS @&ffi,fffd**l #'**-rq r .. ."](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-21-320.jpg)

![r"
Pll0Bl,llil¡r N[(l: 15
Determine la exBtr¡tón r¡ectorial de la li¡er¿a ¡' "' 300.i l4N
Rpta: F 3ooi gooj r 6oo/c
PB0BLDIIA NtrO: 2{i
En un cuadrado de lado "a" hay un cuarto de circunferencia y k¡s
vectores T,¡ yi. Hallarelvector resultante en funcién de X
En la figura se mueshan vectores instritos en un reqbángulo''de lados
a y 2a. Si M es un punto medio.d'é uno de los l#,"dtl reetQngulo,
Determine el wctor ;t en -ftiñción dn i6.riiá.e. '
,11'B - ¡
i:':
PI0BLIIIANf,0: 27
Pf,OBLDillA Nll0: 28
Determine el vector resultante de lc*,"vettóigs . mostradt$j-:p0,la
Rpta:f j.,&
'r, !r
figura
" ttttt'''
?
Rpta: R =2Al"D'
PI(0BLf,lIA NllO: 2!!
En la figura qui se muestra consideÁndo.que P es pur'rto'medid del
vector $,¡¿¡¡¿1 {Ó-X}
en funtión de urx¡ de lós vectoreg.
Á¿s
npta: ¡_i=_E2
l
llbícanos en la Av. De,la Culturs707.6,{ltcntc a b .AN AAC) i:
m<xt¡adrx en le {i*rm, tletennin¿¡r ei módulo del vector.É -- 2 D.
PI¡OBLr][tur NIt{h :}0
Si li es el veclor rmultante <ie los vecto¡es Á,iL,eyi}
,*. Rpto'ñ-lñ=0
CrA. " Si
., Ó. rtdl".
"l
ralor de rx.i* á.
-)
E
Plt(}Bil¿ttñ ññ* *t
Se tienen los siguientes vectores
Á.Érc.i r)rÁyl'
Á r n+ É,,,,fr, y crB r IÓ
ftta¡'A'#flc 4'
ptrlr.*l,sua NnO: :l?
En la figura se mueskan tr€s rector'€§. Detemine el vector unitario
en ta dirección del vector (Á I B I t=)
--:--tX ::.t ;rj i.:i.i;
-(s- 4.)Rpta: u =[Jñ,*ñ,
)
rPf,{lBLlllIA Nlt0: Il!} ,:,;:'
Dado el siguignte conjurrto de vectores, qüá'Lstan ubicados en los
:,iádos de-un hexágorió regular. D_e-teriirihe el vector unitaric¡ en la
dirección de:
F = Á*'ü+ó*ñ- ii+É+ó
g',:'J:rii -t:
€tr
-Bpta
PNOBI,üUA NRO: :I4
Respecto a la recta I.. que se muesha, indique cuál de las siguientes
proposicionessonvercladeras, ti::'!iri': !
I.El ,""to, |. { ,! 7 |esunitarioyparaleloalareciaL.
I s s"-l
II. E[ vector A = .-9i +'12 j ."parátelo a la recta L.
lll. El vector B = 4l + 3/ ".
perpenclicular a la recta L.
...:](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-23-320.jpg)
![AffiáeÉriá $s.!ileol* *.¿¿ 6wdc
?lemf,ila
Pn(lil,DllA ltf,O: ll{i
Si los médulos
ÉyQson,lÉl soNrlol
Z
Rpta: I, Il, il
Rpta: Q-"315j
los vectores
f'lalleF PtQ
El..vector .ñ , .uyo módulo es 300 corresponde a la resultante de
los vectores PyO Determine Q (.nu 0 ., 5/13)
GRUPO G/ILILEO
PnOBLIIIIA Ntt(l: 3.9
Hallar un vector perpeñdicular al paralelogramo definido por
É*(.ñi nt)nl v Q'.,:Lrn v cuva magnitud sea el área del
para[elogramo.
aet., FxQ=-.tii
PNOBLBTANNO:40
Los rxr:tores de la figura tienen magnitudes
P 2m yQ 3m H"rh (p.rú)) *(P.0)
un segundo mas, ¿Cuál es la wlocidad media (en
? Y ¿Cuál es la rapidez media (en m/s)
Rpta, ;' (l'5i t's[¡m/s
. v',,J¡¡/5
PROBLBILII NtrO: 42
La figura muestra un cuadrado de lado L y un cuarto de
circunferencia. Ilallarlaexpresión del vector C '
"n.funcitin
de
o,ylosvectores A o I .i o,t f
2
de
52N:
,1i1,,,,,",'' s;." (PrÓ)"(¡é)=''n
uryw¡u¿Nffi,'*r ,,:,,i"
& parte ciiitlp1#0,$,,h+ci'a- B con veloci<iad constante y tarda
1 sql inmedia va de [J a C también con velocidad
Rpta, Fr 0, a¿ü|c ¡ t tzk
Pf,('f,LtllaNnlh il7 ;=..
;,,ii+,#,iijil1
lndicar la veracidad (V) o.,lalbedad (F) d$"l&s ppposji#lÉs
siguientes: jl I iil'' , ii{ir''
;i; "
I) Un determinado v--qi:tiir puede tene.¡¡, comoi:,; áxirno 3
componentes. .
II) Para AxB- Q; enlot
Ill) Si se cumple i#JB '. fl. entonces uno de los dos vectores (
Rpta: F V F
Á O il I n*c".uriff;-l:r,,19 tiene que ser nulo-,,.i
,:1:
: .::::i::i¡ti,,:l,i).]
PnoBLBilA Nf,O¡ ll8 ''1i*
Iin la figura se muestran tres vectores Á, tiye , halle
Q*r)+ e
Po;>
Rpta:C =-a(A+B)
PIOBLEIIA Nf,0: 4!l
siv ¡ I rd.., Q-- y
lÁl:t,lrl = r, lc l,=2.
Determine el ángulo entre A y B
Rpta: 0'* 600
..:¡TrX Tienes'et Fotenc,ial. Nosotos la Experiencia.,.! ,
NtrO: ll5
'/i
Ret",(7rB) r-(: - s7-r 4J.r sk](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-24-320.jpg)
![EF-:'
PA(}I¡IIIUA NltO: 4,I
?:j"*'il" . ul.
ll .,,f t- B l-C
vD '5u
rnódt¡lo dé [a Resultant¿:
+D'lli ll¡ .AdemásF., 13p
Rpta: R.-3§¡r
t¡ttoBLlirra Nnoi 45
[:ir la figura adjunta se muestr¿l un conjunto de vectores, determine ."*
el módulo del vector ,'
/i-, s¡ 7i' . Á r I t C' t ll.lD 1.,t1¡t ....""' if
5
Itr;il
PR0lrlliltlA Nlt0: tli
I.a fi¡¡ura ¡nueslm una circunfererrci¿r inscrita err tln cuadraddr'tallar
X en funcií>n de k¡s vech¡res A v ll
' ,it.!l
rrnta,'lF],.i25"
f
Se tienen dos vetJores unitarios en el plano XY: p1 y ¡t2. pllfoima
16" con l¿r tlirección I X y ¡r2 forma 69" con Ia dirección l- Xi.:' l
t'l
I u, .r u"l
Ilallar: l' '. !.:'l
I P, t',1
Rpta: 4/3
Plt(]ll[I]iltA NIl0: 4fl
I)¿¡<ios k¡s veclores: Á " 4i r $v
;-' t2senl j . I'tallarelJ:rociuetovectorial A x B
Rpta:/'¡,21^[z¡
5
Ptl0BLlllIANIlO:4$ ''r r'..,'
En términos cle los vectore.s i, n' , C 1, D. Hqltot
Z-l t É a' t; del conjunkr tle vectores moshados. La figura
es un paralelepípedo ré<lan1¡ular'
llblcanos en Ia Av; De'ld CuluiralhTí'(frentea'la UNSAAQ
B .', 2cos8'
PR0ll[llllA NIt(]: f(]
fua:ln[=31., , lri . :r,: i, i, ' tr.-..tr.1i{
Calcular la suma de los vector¿s
-i
v I . que se duestm en b
figura, en clonde M es el punto medio del segnánto PQ
A=700u B.-650u
ri rl¡ir' ,.i' 'i.
i+ ¿soü
R=(-1,2,3),. HallarEl
Rpta: R:400
''-"-,, RPta: Áou =.r6Op'
RPta: R = 34'6m
?noniBila lttrll: 14
Si la resultante de los vectores que se indlcan es nula' Cdcular el
valor de 0.
Rpta: 0 = 0o](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-25-320.jpg)

![r-" ;F§§i:*r. .-
PROBLIiIIA NBO: (i¡-¡
l-lallar la suma de los cinco vectores mostrados de ig¡ual mduto "A"
Pn0BLEilÁ Nlt(l: (i7
Pf,(ltrñ,S![A r§40: Sf]
F.fallar las componenles de Ir en los e-ie.s que se ntuestra.
Rpta: 14N y3CH.¡,i
Pf,€f,üSHAñR$: T{,
Si G es el bancenlro del triángulo A0B y M es punto medi<¡ de ab.
.l:xpresar
el vector ,Y en {i¡nclón de los vecto¡es Á u B
! ;.
-
.'-;
Rpta: f =.4:!-6
FROBLBTUII NII(): 7l
Cdeular el mócluló tle-[asuma d¿ los vectores A, R y C .Si
lr] ;,B, lq = 3. iC -- 5 ,¡2.
Rüt¿:9m
li1,: wfilrñfft ?r.,.
I
Rpta: ¡=[*r)t",u¡
PnOBLR,lIll ñlt0: 7ll
I:n la fi1¡ura. Si M y N son punlos rnedi<-¡s de PQ V QS
respeclivamenle.
l{allar el vector unitario del vecbr MN.
Q(6,e)
s(10,1)
iiiLuu..i'r+.t"r ,Íü función de tecto.", I / 7i , si M es el
punto me-dio del cuxlrado de lado L.
pffimlaN*ü $4
Determine las cornponentes rectangulaies del .vector, A. , ,9o la
dirección de l¿rs rectas. Li que pasa por (0, 0) v'(a, 3) L, qüó pasa
por (0,0)v (-3,4)
Á.=os,zol.
nptu, I ."'{24, 7)
I-.n el paraleloqr¿rnro ebcd, hallar et módulo de la resdtánte Si
A,-4m y bc -6^
Rpta: R=l2m
PII0BLIIMA NIl0: Gn
I-a fi,c¡ura muestra un rectárngulo. Determine el módulo del vect<x
resultante.
I n, f- t2m
--l Rpta:26m
Ubícanos en la Av. De ls Cultura7076 (ÍrCNe a la WS*AC¡,
1i.
5m
i,' M
ri
X](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-27-320.jpg)

![r¡fsrce r
Pll0M.ltMrl NIt(l: 1l,l
r"
i''it''
cur.rl., el lÁ .r Éi ,.i A ',, 20-u''iu y'I3'" 30^,Dtt
tjn vector A c. Rl fonrlu 45' c.rn el el¿ x yleo" .* {ei" V,
I lallar sus coordenadas si A ' 20m . '' . 'i
iii,,L*ffiI.[rAiHl¡o. , .. ,.,
:,.,-.,..,,1- *
-ft.1..9¡t9¡
C gs,perpendiCular a tos vectores A v [l , el árigulo
enrre, Á yrli ., de 3()" Si A 6m. I] ,3m, 'C,-3m.
Calculi Á vpltrmen del paralelepípedo.
l;-n el sistem¿i v<¿ctorial se nluestta cifico'esqut¿r-r¡a5 f¡i¿t.1gt¡lar,es,
todos ellos similares. tlallar el médulo del vector suma del sislema:
Rpta:40 nt
PtrtlllltillA NnO: 87
Calcular el módulo del vector resultante.
R¡ta: .Fo = JI]¡f
Pn0Bltllrt ilnl} $S
Se dan k» vér{i«:s de fr" tdáng,rlo. P "(Lo-L 2)
$ 0=.(5, *6,2 y t-,{1,3. -1).f,alcrrl¿r la.bngitud de su
ah¡ra, bajada desde el védice Q al lado 3§.
i;l
R :i.iil; ;i !ir¡ii,r,:,
Rpt¡: fu
= 5m
PBOBLBUA Nll0: ll$ .,,"' ,
A parlir del gráfi«r: ¡;.:,i,.','.''
b) run", z(iJ+ c) t ' "
,,
._J-
c) I lallar el producto escalar de los vectonib" .1
¡t
Rpta: V =,27 m3
Rpta: X =
rn
3A _48
Ptl0llf.llllA NIl0: 9I
Haltar ien función a" Á,8 y e , si G'es;¿l bhñieÍüo del
triángulo PQR y E es un punto cualquiera.
apta, Á:(to.D, t
R7tg: A =, (+, l, -:)
zla t c) .(
Á.ó -' q
..'Ptl0$tDúaNf,o: 9o i;,!,.
-Se tie¡¡án'dos vectores cpncqr.rentes 7 y: A ; Hallar el vector
'' '.;[ " en función de A y B . sabiendo (ue su s<tremo divide
.'r,1,:-t,|:i7 en dos vectores iguales y su origeii diüide.a T . como 2 a
7,
3u
X
t,,.'i.
./* 14s
5u
llbícanos en lo Av. Ire la,CulturalDTíl(freare a.tit UNS1VIAj t i](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-29-320.jpg)
![-
:;1;.i. ffiEftá;iij €-,+;:F:::.':::: ri :,4 ;
PBOnLflñIrt ñIl0: t(Xl
Si la result¿.rnte «le los vecfores de la fi1¡ura es <le 900 N. vetlical y
dirigida hacia ahaio. Clalcul¿r el valor [r2. 'r. .,
Plt(»lLBllÁ NR(l: l0l
sil:Á r z{ :om,
lzÁ :lll 25nr; cor.uru,,
lzÁ +el
¡Á r zii
Ptt0Bl,l:ilIlt NR(l: l(12
l:xpresar X ,n la función cle los vectores
B
T
.;::i' :,:r.1.
+;i -:',1li.t'r; rii::l::il:
'*§+§fl
lllilli
iil.§ii,,:i
:: ii iiiii
^,i(, Jz[ri , n)"
fr) )i (o r[a , n)
c)i..ArBT_
J2
r'{&#anoi' b¡ I a'Ai; D é' fa eahrird I' 0I'6''(fti nte a I a U NsAAc)
).A lr-)
PBOtil.liIIrt ñItl!: l(13
Calculár'el valt¡r de tr, para que [a resultante de los vectores
mostrados sea la minima.
Rpta: d ..22,5o
PR(lM,IlUrrNR()! lal¿
si
lJ r ,U!,r,, , x pl t
$-'15 ; calcutar el módulo de la
resulla¡tede:',1 y B;
A+ 28
.r.i
Le,ffi& furft1:f,=ig
PñrBLlltA NnO: l0l¡ --, "' .-.1;,1"
En ét'$ralelogramg á,'b, c:
lld"lga',
*
Il"
medio del
i"grn"rrCI'' t4airesar el veq¡orfi en función de A ] B.
PBOBIJIIA ilItr(l: I(Xi
Dado los siguientes vectores.
""tf., lñ.1
- A-B
RPtr: .,Í = ---:-
J
. SiC:3m D=5m.
D
hpta: R= z$gm](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-31-320.jpg)
![tr ,F
Acaáe¡nia G'elile{}
.é* aaa¿ 4q¿*ée
PnoBrlullÁ Ntto:
Hallar el vector
cuadrado.
I07
X e,n función de
B) 60"
E) Nin¡¡uno
qa-B
E) Nirquna
I3. I-a ii¡;urá es unAy
GR"t}r,* GJ[r-rL&CI
PItOBIll,llA ñlt(): ¡ t2
Si, A[]CI) es un irapecio is<'>sceles. escribir i en funchlt¡¡rde
.,,
¿¿ .r' l, ,i¡l ,t/ .Vi J
PllOIlLltUlt Nlt0: l0fl
Se tiene dos vecto¡es de 4pal nragnitud que ángulo deben de
foitnarpataque la resritaritere¡*igual a uno de ellos.
¿t * b ,Y,"8
A).-.- A+.ta
n ; niÉ1
L t!9»
Db-ct -..i$Íffiunu
:'i
l,ROIlLIllIA NIIo: I Il]. !i:
A) ll0"
D) 120.
c) 90o
PltOlllIiMA NIIO:
-
I0f)
Escribir el vedor X en función
"
á y b
M: punto me<)i<t de iÉ
ü-bA)-
2
Blá+á li) Ningun<r
PMI"EilANll0: ll{}
Fldlar la resultan& de
circunferencia es 2
A) 2m
B)4m,
C) 6rm
D) 8m
E) I{iry¡uno
trmffiffi ril
Escribi¡: .f enfunción e A y
.,,.:,1R" es el módülérdel .resultante {l} 2 vectores cuyos rnírdulos son
!::::,11,.,:-V "2P", sie@El áng¡ulo end sus líneas de accirin de 60ó, 1a6
' cuáles actúan en'un,pnte"Of{Jn tercer vector cle mridulo "S'' (S
> fi) actrra en "O".'S.é1 máximo y mínimo v¿rk¡r de la resultante
de totliá$ü*,g.,ectores es de 2,6u y 12u, delerminar "[,"
.:.r
At.J7u ''' ' wltlZu cl3tlTu
:;.,..._
i:=:r:1 :r,j
.:!,:.,, 179U -":t ''¡-7U
ri .j
ÉnoRr,ll¡tr,xt0: tt4
Si, (l es.tLáricentro del triángulo AOB, y M es punto medlio <b AB
[:.scritrir Jf en función de A y llotbB)-
2
.::]:.}:1
:.i:i
:lii?j l;eiri::g
' :1i.ri.:.aj:::ti;-
+,::iiii1,:t::r:t:
:ir.iiq:rt:r1,
'i¡::r:.:.
C)a -b
e¡atb
2
-;
DIA ,D
3
pHltl,nlt¡tiffi ¡la
En la fig. detffi*¡isrtr d woáSo da h resultffnte de h6 §ñ&
nrdedm.
a¡á't"6 cl q +¡
43
E,!e@
i,
Ala +á
á+6
Dl_-'2
b--a
ct-.,2
A)5
- Dl I
B)6
E) 10
c't7
¡§ ftaes d Potm cial ñam§:ac fu §pcrtack,.,I](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-32-320.jpg)
![FI§§CA T E&áBffiffitr;ffi. S
proBmrÁ ñBs: rI8
i.."f, trdr"'i;1ir.unfurn,,"iu res is 2cm tte raefi,J. $,6te"i*lrte ¿i
vect<¡r rcsultanic
PIrütrImlA NII(I: I 17
Si: ABCD es un paralekrg¡tnnto y "M" y "lf son purilos medios
h
"Ao.
Ae o para quc fa ni¡rma d¿ F ea vnhüaa et
a) arcee 1?113
b) arcc<x 5/13
cl75
d) 52'
e)42-" . , ¡.
PR0BLts,lI¡t ñBO: I2I
ün .i +'B n*' '
a) 4A cos 0
tr) 2A cos (0 -t' t)
c) 2A [cos (0 | +]]t/'
dlA(10+ 6c$s(0-$))1¿
e) Nin¡¡uno
PIIOBI,Itrü,I NTT& Ig*
l.a rnag¡nitti<l tle h resqltante del siguienté $§erña & t Gc&§§@ Ét:
t(
U!r'vector I tt"* un ámgio { con el & hÉ X. kWdfurBk
vecee rrás grandc .qrry A furce un ángdo 0 ryt$ S,&,Sr q
a¡Éhoá üectoi?ase árrcuantran en eX n*r'rdie¡@.*§¡:ffi&d .
AB y liC re.specfivamente, hallar X
A
Il)6 C) ri
t-.112..
)-
u1(A t n)
I
»-ltA t BlI
L
en lémrin<rs dn A Y B.!
M :.. :'r'i'r§-'
;,O'r-'
A)4
Dl10
p
úSlé vi:ctor debe suna*e sl veclor
[t
.:OU ,y' que hace 60'
con el eje X posilivo. para clar co:n<> rcsuhante el vector cero?.
¡.':::-.'
l,l:,iile f¿r n,."r"
a21' b) 4'1' t
'.-- c) 20 ?3
dl2Tl3 e) Irallair datoí" '. -_.'. l
PROItLEilIil. NRO: l2:l ." 5 ?-
ft-.án$i1ir, ót1!r€,: dos vectores de lp y .S uni8a¡fes de loRgitud
cuand¡ ,réiültante tiene 20 unidailps'i:s: .,j:{.i:-
a) arc cos 0.21i .-r.'* ,,r,¡,;;:'""
b) irc cos 0.71i ,._...,,j .,,,rfi,
c) arc cos 0 ,,. ' _ .""
,-,!' ,,re) ningún valor'
*"i;p","'
PttoBLuuA Niro: l2r.l
-o
f:l ánsulo entre <los veek)res de5 y 1ú unidáfi!:§ d.#&ÉSitd'¿t¡¿*¡do
su resuftanle fo-mra unángulo de 30o corirll vécféiriÉnáy.ot'es:
ffil0l§¡lrl¡rr ñi¡(l: I l.$
a) ItO N. (t 240"
b) ilo N. o 120"
c) lfi N, 0 3()'
d):10N. o-,180"
a| Iin¡¡una de las anÍed@s e.s correcta.
ptoBltrr[A EtHh r lt)
$ q4§.§rg 'U¡.hir¡ro de wrjtcl'rss & dilerentes
feu#arle e§+ero <s:
. :' .'
E}ee
bles
elifts
d) cnaro
e) ning¡rno
si'l7,.,,Atll
1*
ier
r{d+EJ
l*
ctTut-t]
1-
ell{a +'r)
1'
t
a) 30'
d) 37'
b) 45" c) 60'
e) 120"
1.-4.
! 11.
;,. ,:,' .'
. n$f: i. -
't" :'. .
'ii!.1. - I .
:rL.:. ,,
magnitudes ci'rya,'
PltoBt,D,lIÁ NII(h 125
I)ados k¡s vectoi.¿s. I ..t. B delaüggñ'*§e@el&ñl§s §i$+*g¡fcs
identidades podernos afirmü$qte
I) ilt'El=? lA + I§
Ir) lA - Bl: lA r Bl
¡¡¡ 2lAf *}§f j 1r
lV) ?A *S
4)lH[ §sn crtr@bs
tuItú il*¡on edrf¿ctɧ
rJ{l v fV son corrgc{as
d) Todas.son coüsCtáa
e) Todas sprl inconectas
F ,rq$
,d>-Á
*
¿ruúr .üEee,eWffi6@*ln#ffiSae$.",;,](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-33-320.jpg)
![i
t4i1¡l:jiti::¡5l r'A i'-r'
_ .S r:- ¡r{.É,i,r.:ilar;.+;:
"@.'
€Ír¡,rpo GALrLf,o*lifá Acadc""rrrtg
PIlllBLli.lI¡-tW:[ZS:.;. "' "1{'r';-!11i
' I :'riilrii¡':':ll'ii'rl 1r'"irn''¡";r1r1:
[nconknr el módrrlo dt¿ la sru¡¿r <Jc los sigrrier)fes veclorcs
rO; Al3, OC y C(i . s¿rbiendr¡ rlue el cubo es <ie l¿'rdo I-:
a) Paraielos y de senlidos opueslos
bi Paralelos y clel mismo s()nti(lo
:.' ' : "' ' i''l
c) Perpendiculzrres "" " ''
''.":
d) iguales y fomando un /rngulo de 60" entre sii
e) nin.r¡una de l;rs respuesia¡^ ililleriores es cierta.
Plt()lll.l]llA Nll{}: llil r':.]:
Sean bs ver:f o¡es <xrpl;rnarres i.
il,3i2i
h t2j:
su prorlucto veclorial es:
a)0 b)4k c)k .
d) -4k e) k ':'dL.J'
dll-
b't2L,[l
e) 3l-
t
.lL,{l
PIlOBLTHjtNru} I27
La mag¡nitud de l¡l suma de lc¡s siguientes v{rctor€s:
t¡::=¡:',,1.i:l!
.lj::J
Ñi I f"ñ r i*i r ne , sabiendo que tós puntos C, r, u, r-, .t y
K dividen en.3 partes iguales los lad¡x de los trián1¡ulos equiláteros
AUC v l)l:F de l¿xlt-¡ I., es:
a)'?.1.
b) 2tJ!
c) I-
d) 4rlrl
e) Nin¡¡un;i
p, NnO: Ilii};,,,:,.:,
Dado l6i:veci ei,.O
_',,rt,
B . , 2j, C.:2i.l.a magnitucl de
fx (ts
I C) es: .:
' u)ts
Bfu* i
c)'s;:ti::.1;ii:;:i*,:::i :: : ,.',:.iri;
d)4 '
e) 8
P¡TOIILETIA NRO: I:I4
:,'¿Cuál cle las si¡¡uienies afirm¿rciones es correcta?
ui Un ,n.to, prr.d" s.. c"á a pesar que una de sus compon€nt€s
no es cero.
b) Dos vectores de diferentes magnitudes se pue<len cómbinar
pam dar una resultante nula.
c) 1'res vectores de diferentes mag6ritudes, se pueden combinar
para dar una resultante nula.
d) Si Á. E - 0 entonces, siempre, Á ''' 0, n == O
e) Si Á x É 0 ehtonces, siempre, Á:O n=O
PB0BLEIIA NnO: t:15
Dado los vecte¡res A, B y C perpendiculares enhe sí; con las
maEnitudes de estos v€ctor€s se forman un. paralelepipedo
rectuigular de aristas A, B y C: El volumen del mismo se puede
cxpresarcomo:
a) 2(ÁxgxÓ)
b) Á. (B xeyz , , ,., .
.l 2Á .ts x el
d) A.(BxC)
nl Áxexe
r.i::ii.r
I :::t: l::r::i :rr!
t¡ll0BlDtrlrl NR(l: l2E
(luál de los veclorcs expresados a continuaci<in es paralelo a[ vectoi,
i 2.j"1 3k, tiene dot¡le longitud y sentido opuesto:
^t Jri,t,[l¡:iJlt-
b) 2i 4i-f¡k "
c.Zi t 4i (*
d) -i + 4:i - 9k .,,,,,ii:r'
e) Ninguna rle lm anterlgres
PIIOBLüMANB0: I29
::! : ,'::i. -.
l)ados los vectores:ifl ' ,3i I 2j-7k; á ,. Si r Oi.5k c ,..,2í+ 4i t 2k y
l¿ls siquientes pro¡¡xlci<rnes referidas a ellas: i,
l) I)os dc los v-g¡tores tienen su resulhnte ig¡ual al tercero.
ll) I-os vedr>res present.n una figura cerr¿rda.
ffl) Los veclorei no preseritarr* una figura cerrada.
l)c¡demr¡s afirmar que:
a) I y II «rn verdaderas
b) ll y lll son verdaderas
c) II y lll. son falsas
d) Solamente I es verdadera
e) .solamente lll es falsa
I{t0lllllllÁ NII(I: I ilo
Se lienen d«¡s vedores i; y Q a" manera qu" P- t"p ,.., F . Si
se cumple que:
IRI, IP QI'
[)e los vectr¡res P y I * puede afirmar qu€ son: .
¡T{r,:: f ieaes,el.Pateneisl. Nasotros la Íxperiencia.-.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-34-320.jpg)
![r
üt¡fltLllMA NBft lilG
I)os vectorés A y B forman un ángulo de 45'entre si. Con relación a
las siguientes identidades :
rl BxÁ-AxÉ
II) BxAiB.A
iil) ÉxÁ-Á,s
w) lBx Al: lA. Bl l
...
vlA.B-B.A
Podcmos afirmar que:
a) I y ll son verdaderas
b) lll y IV son veqdadcras
c) rcic V es verdadera
d) IV y V son verdaderas
e) Ningrna de las afirmaciones anteriores (a,b,c,d) son verdaderas.
fBilrñtÉlll ñrB$: l$? .¡'
De las siguientes operaciones: -.:
il) Á*s.e r:-,0',,,;.':'=i i.
ru) iÁ . el x i "'"""j"" " .,. .l;
ru tÁ rjl x (e . ill '"' '
a) l, ll y lll b) l y.ll
d) III y IV e) II"y III
PROBLETA NBO: lil8
c) I, IIyIV
iCuál de los siguientes vectores es un vector unitario? ..
..
a) i+j+k
c) 1/3 i + 1/3j - 1/3 k
"l€¡-{,*{'*3 3" 3
b)1t2i-312k
d i t"tl'2i,..112k
Plt Bl,DlIA Nlt0: ll|$ .:
Determinar el módulo de lá suma
S: re , r'c + ñE Fñ.
(Considere AB '. AD .,sr[Z t. AH ',. lel)
de . üi?elóres
Al26L
D)10L
B)17L
E2 Jsl L
Pn0BLEtil NiO: l4()
Dado los vectores 7 -, Xi, Sl 2kv I
el valor de X para que el vector (1 U
A)1 Bl2.s
Dl -22 E)8
qBJ' L
,., -i - 3j .1.. k; determinar
seaperpendiculuro l.
c)5.s
llbícdnos en Ia Av. De la CulturaTol6 (frente a h ANSAAC)
PBOBLIIHA NB0: l4l
Dados los vectores:
Á,.gi-Z:
'rt
ñ, i ¡i rst
Ó,.,zi-t-j-+u.
y las siguientes proposiciones:
I) Á, ii y C fonnan un lriángulo rectángulo.
Il) [-a suma de los kes veclores es cero.
III) Uno de los vectores es la suma de los ok<x dss
N) Á, E y C n., forman un triángulo.
Podemos afirmar que:
.o- a) I y III son correctas
I b) II y IV son correctas
c) Solo III es correcta
d) Solo lV es correcta
d)'todas son incorrectas-
Pnml,f,E¡ NI0: l,t2
I-as diagonales de dos caras <le un cubo, OA y OC se ihdican en la
fig. El vector unitario, en la dirección y sentido de OA x O(l es
{et cubo¡&idti.lado L)"' :
t' 'r;!
.A) {.i+j{ k) B) (ir i:,Fk)'" c) (i+ jt'}iv
,t
D) I (irj-k) Ii) ' (-iljIk)
':: 6'-.,, ,.' .6
Pü0BL§llAttO: l4ll
Sn"n.,Á,B,C tres vectr¡res y m. n escalares. I'ln estas condiciones
se verífica:
:])
_,,,r0
'.i. I0
v)
mA,. Am
iun s'tÁ
(mr-n) 7 ,.,^"7 , nrt
,q+B -c.,,,7 (7 t n)
A) I y IV son verdaderas
B) II y III son falsas
C) II y IV son verd¿rderas
D) III y IV sort falsas
E) Solamente IV?s falsa.
PEgSt EIIA NEO: 1 44
Dados los vectores I l, I , tales que
G ¡ I ) es perpendicutu, u (l -b); entonces se debe tenerque:
A); "" 1'
a ;.b,., ab
Cl la xál o'tt
D)
l;l lrl
E) ninguna de las anteriores.](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-35-320.jpg)


![ffi'X*uA*q**
PltOllI,EIIA NIIO: 157
l:st;¡blezca la veracidad (V) o la ialsedad (l:) de las sig¡uientes
llroposiciones.
v. si ;:6i'+3iv
ii ,,,2 j * i, Á* li ,= (ti
vr. s' ,i , Zii' tj-rk v
ii =zi j +»k . Á.li ,.. -36
GRUr}Ü T'AI.ILEO
A) 3a v (11, 13 .1) B) 3:] y (-11
D) 35 v (13, -11, 0) I:) 38 y (12.
i;) i36 e (11. 12, 13)
Plt0BLlIillA NIIO: lG2
Determine el móduk¡ de la resultanle del sistema de vectores
mostrados.
,2ú4u
3u..t
D
Vll. Para cualesquiera' vectores
(Á" ¡i).C ={Á" t})x Á
vur i'x j *i =.(í
"i).itt) vt.trv
L) Vl:rF PItllRLlilIA NllO: 16ll ,
Si P v Q son ¡:unkrs meclios dC
,,,1,,i..ul.,,I
:!;
lqs sesmentos ABv BC ,
A,B,C
a) 10u
b) 20u
c) 12u
d) 5u
Plt{)BLlllIA NtlO: I i¡{t
I Ialle un vector unitario ft al qun el producto escalar
( ,¡ .¡)., sea mínitno
n(zl i)r.ti a(zl "t j)tJs
D)( 2' ti)tJi Et(t i)tJl
t:t(l"rj)tJl
Plt0llLllllA Nlto: 150
sean los vectores d = (o, a,)v 6 * (bu,br) .uyu r".uh.$
-
'tt''
es de módulo 3. S¡ á.b =. 3 , determine d uub.
9f ;rr,,... ,
p=ai|a:+"4',bl ".'r'. I
A)1,5
D)3
respectivamente, dgfg$l¡tl ,el on"tun @
,, c) i"[i2)
i;i:..;4.),,'l.t-z'
¿l
i.$ ( 2,2
A) FI:FV
D) WFI:
A) FF]FV
D)VFr-V
Lj) 2,4
Í: 4
c) Fr-trl
c)3,6
trnOBLIIlIA NIIO: lli0 :'r::#
I)ados los veclores d v t; eslablezca Ia veracidacl (VJoJa fatsedad
1, t::: " .4. .......::: -
.ll. 'i:ir:i:':;. '::
, L-a:::a
perpendicular a á ,
(F) de las siguientes afinn¿rciones:
n.x h
I.
-:
es un veetor.
ri.b
rr (a.t)n (axr,).t
m (a.o)(u,{a)=(ab)2 .'
N. (a
"U"t es un vecror
/
necesariaméñ.te
B.).i{.F,f.V,r,,,,.,,-j,,..::,.i1 ) VVFF
LII:VrVliIVr,r,,r,,',l'
Plt0BLUMrl NII(): l(il
Dados k¡s veclr¡res:
ii,=i +2j+3i,
b=3í t j+2tiy
é =2i r3j +l
I lalle:
M = á.6 -16.é + ti.é v
11 ..,fi"É+ixé+áxé
PRI)¡lLtllfA ñltO: l(i,l
Un buque navega mar ¿rdentro con rumbo a[ sur; después de
desplazarse 23 l«n; camt¡ia de rurnbo hacia el oeste naveg¡anrlo 32
km; finalmente cambia de rumbo E l(f N ¿rvanzado 25¡ km. l.Cuál
es el modulo del <lesplzuanriento efectivo <iel buque?
nlz r/5 t*. u¡ :1 ,"3 tm cl¿ ",'5 r.-
ol s r/5 tm. E)il.V5 km.
I'll(lBLll,lIA rYIl0: I (ir-r
Determine -X en función de Ay ,Zl , satriendo que PM=,SMQ y
G es e[ baricenho del triángulo PQR.
38* A
6
D28* A
B)3 R- A
-) -)
3 ])"r A
F)--
2
a
-r+
3 B--2 A
c) __,6
a)
fM
,¡Tú Tienes eI Poténcial. Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-38-320.jpg)
![r ,iulffi? ¡¡i.:."a"..
§.I§ICA I ACADEMIA GALILEO
I,llOtlt,IilIA ñltO: l(i(i
Se rnuestra que un trianlJui<¡ AIIC, siend<¡ el punto C su b¿rricentro
I)efemline la Ilesultante del sisienr¿r de vectores cl¿rd<1.
PROIILIItrNA NII$: l$7
Se mueslra un sistema de vectores dispuéstos sobre un hexágono
re¡¡ular de lado 5 u. áQué módub tiene la resultante del sistema de
vectores moshados? ,¡-
PII{»ILBüIA Ntl0: l7o
Iin la [igura se muestra d<¡s vectores dispuestos sobre un cubo.
Determine en que relación se encuentran los médulos de los
vcctores A,Ey A B
¡
I
I
)--
A
B)0
l])i
Al2
D4
c)3
j '.. lrr rn qu'l .¡ iq r'i i¿]
(t
".
.e a "¡, e" üu lo
o) € ioole'
á-t "l]
-''
1
A)
J
"J5D) --
2
PROnÍDilllNEO: I7l
5i tiene un hexá,go¡o.regular de lado 4 u. Si d¿ uno de süs
vértices q$rldJü¡p¡e2¿ ¿,.,''fra:ar vector€§ dirigi&s a cada uno de lqs
* s, áilié módulo ti¿ne la regultante de sisterna de
Bt
"',
^t;
c) --
J
A) 2Ou [3) tOu
;¡#rl , I:) l5 u
"{./
,d' pnourunrA Nno: l(ilr
Setienptiosvr,ttores "4,,' B ntl (orn() semueslm.Si l/ -lequ;1rl
r.Qué valor liene l¿ res'rllalrte rle eslos veelt¡res, .i ." ,a q*i,,
C}25 u
c):21 u
,.rect¡f"'"'rs si su módulo cs
J :t.
;+,
l,ril 'r'-
mínima?
A) l6u B) t3u
I))6u I:)12u
:lr:,:.tJi;
-r,iiÍ:if.,r,ii
4
,.'
A
C) 10u
C)12u
A) i+3.i+f,l,llll¡tlliltll Nlt(l: l(if) :-
l.a fig¡ura que se mueslra eé un rectángulo. I)eterrnine el módulo du'
la resuli¿rnle del sistema de vectores mostrados.
12*Jq¡
t+-l*K
2"
c3í-j*É,
ol ir-j + k
1
^^
I 4 f
Fl-J/ +-t+k' 1'
J
I8u
L
T'), ,
I
I
fiu
L
A) 8u
D) 15u
E)10u
E) 18u
F-- 6u
--{
Ilbícanos en la Av. De la Culturel@76 (frente a te..l;tltffiA€)ii {:t:](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-39-320.jpg)

![r ::e¡l*?t'r¡3ir j,,§5I¡: ¡a+!: ':.,"?
¿&eacl*m:ia {]alí}er:
in ,., Posici(»r inicial
i:¡1 ,,, Posiciirrr linal
ii ,clesplazat,ricnto l.r
eT
t'¡
v nr¡r
t..
MovIMI ENro RECrI LINEO uN I FoRM E (MtBi,ffi#,¡
[:s aqutit movirni¿nto cuya Lriryeckrria és uha reela y'ltx espacio§ igrale§ son r¿ri¡rridos en tieinijos ig¡¡¿iles.
Iil espackr es <1ireL;i;rrnerrle proporcir:nerl al tiempo. .-; .:,"
- I-a veloci<]¿rd es c<¡nstanl.e.
.. l;r ¿:cp"le¡¿¡ciór¡ ¿¡.. ., 0..
cl c.l
-...
€,, , ctc.
t, t: tD
-ee
v c- vl t .
tv
lvi .,,,m/s. crlis y knr/h
d i,,
RAPIT}}-U ME,DIA.-
I:s eJl méclulo de [a vekrcidad rnedia. . '
ITAPrDIiZPROIIF.DIO.-
l] üfla ma$rifud escalar que mi<ie [a r¿laaiór¡
entre el espacio tirtal recorrido y el tigmpqr total
empleado en su recon'ido.
.d'a [a 'Vl >',
vr --v:
ft q-
vi'+ v,
MOVIMIENTO RECTILINEO UNIFORME VARIADO (M.R.U.V. ).
CAHACTI:RISTICAS:
l. l.¿r vek;citla<l varía <¿n I'onn¿: uniforrne v ' ' variable :
2. l::n iguales interu¡rlr s cie iiemp<;, el rnóvil experirrienla los, rnisrnos
unilormemenle c,rtt el iicmPrt.
carribkrs de vekrcidad, ets tlecir que la velocidad varfa
*
3.
a ....: t :=
t
FORMI¡I.tts:
a(.i- ) rnovirnienio aceler¿rdo ;r( .
) urovirnierttr., desaceler¿rdo
¡.ti
-§¡
ti.
!:íi:i
i :..1"..
-.- I : :;_',i:
c¡l^ITCO.§ D IiI. ful.R.IJ -
cle
i.fú,.{ i e n g s.,e !
.1.
o + .g
:n
C
ll
ql:,N
o s o Lr o s
!1
Ex p e rie nc!:'.. I](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-41-320.jpg)
![r-ͧICA I
Yt
V1
I . vf ,-,vi t at
2. c.-v.t t!at2''2
- ).,^_1. 'l: : Vi '1.:.
¿Ae
4,
5.
(v¡-+ v¡ ).erl-lIIal
¿)
t,en.
1.v¡ *;u(
.i- J
t"i.
I
2n -1)
TIRO VEETICAL. Cuando se lanza un cuerpo verticatmente }iátiá:,ái.tlÉa con una velocidad inicial v,, el cuerpo llega a b altura máxima (h*)
en este punto la velocidad es igual a cero.
Los vectores velocidad y aceleración de la gravedad en cualquier punto de la trayectoria, tienen sentidos contrarios, de manera que el
moúimiento es retardado o desacelerado (-g).
Nota: la aceleración de la gravedad se utilizará con sig¡no negativo en cada caso
:r¡=et
¡i- 7,¡
Atea: veloeidad
: . FORMUI.AS
I
l) V¡:*gt 2)h:v,tt-igt2
¿
3)vr2 : vi2 +2sh 4r:[].*Jt
I
5)h,," : v, +;S(Zn * 1)
Ubícanos en Ia Av. De Ia CultaralAT6 (Írente s h ANSAAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-42-320.jpg)
![r
ffiA**ácm§W $§[UP(} G.AI*ILEO
MOVIMIENTO DE PBOYECTII,L,§
a) El movirnlento de Lrn pr<,ryeclil es un movirniento compuesto, en el cual la trayectoria resultante es una parábola. Al proyeclil se le
irnprime una velocidad inicial y en todo momento la aceleración del mism<¡ es l¿¡ ac,eleración de la .gravedad.
b)
x =. y,xf : (4 Cose)r
rr:(f sene) t*lsf
..!.-
rk;Yrí1:
ifu
¡1::1:,¡l¡,i..-i i ,-j',
, l:r. .2 /
D;,- JÍ (n*" 0,,,4s")
0'
: I ...t
t
v, "sen20 4h^
D.. --:j-- t00 - --.*
g'D
t,.
hn,
ttr'
1l:.,''.,:, MOVIMIENTO PARABOLICO
c)
d)
Cuando,i!,fr cüerpo es lanzado horizonálmente con una velocidad q", dumnte la caída la kayectoria {el cuerpo será el re§ultado de la
combinái:fu de dos movimientos, úiib horizontal uniforme y otro vertical de caída líbre.
vy gt
v,, I
tgO='Y h.=gt'" v* 2-
a .. 0 u,, -.0
¡ -(v,")(t) a .,, s ,:j cte.
vy - É.clt
1A
. V:SeI]UL __. r
lrm-T-
)c
.- 2Yisen0
o
¿,
2v,2sen0cos0
])- .¡ . ,' '',1
.E'...,', ,,;ii*É ., _.;:1:;
trii'i...t,li:,ii::liri,;:ffi
ta
iTtú Tienes elPater*ctü.I' Nosotras lu lixperieneio,..!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-43-320.jpg)

![$H(lllilillANlt{}: It}
tJn cr>che pale del reposo y acelera a l¡mA' durante 4s, detennin¡rr el
espar:io recorrido.
l'li0Blflilrl NIt{l: 2{l
lJn ¿rul.o que tiene MR(-)V sale con una rapidez inicial diferente dei cettr
y aceleraci(xr de 4nVs2, recome 80¡n en 4 s. h¿¡llar t¡ veirrcid¿¡d ltnai.
a) 24 m/s b) 28 mls c) 26 rnls
di 20 mls e) 10 rn/s
PñOBLIIIIÁ NR(l¡ 2t
(ln móvil lriplica su vc¿locirlad re«¡rrienclo un espacio de [J00rn en
2G. hallar su ¿¡ceier¿rci«in en mis2.
a)2Om
d) 16m
al2 mli¿
d) 3 rnisT
b)24 m
e) 48 nr
b) liO m
e) l;4 rrr
h) ! !) nrt's
r:) 1'l rn/s
b) 60 nr
e) 8Ii rn
c) 21 rn
c) lili ¡n
c) lSmrs
Itn0ilf,BllÁ NII{}: 22
I)os móviles A y [J rlistanci¿x]t¡s 64rn'.. parlé.n rlel rcpoSo
sirnult¿inearnente al encuetrtft) €n rlirecciones opueslas,- con
¿u:eler;rt:iones tle lirn/s' y 5mis7 res¡l.rclivantenle ádesput':s dc cü¿intos
se1¡unc.los se enrrlnlr¿trán'? .r'
i:) 5s
d)2"
b) 4 rnlsz c) 5 m/s'z
e) 1 ¡n/s2
tr) ,3 s c) 4.s ,.¿r
e) l'(i ,s :
b) 12 s
e) 16s
c)'13. s
PII$BLIIMII rYtr{l¡ lil '-I
I)os mí¡viles A y t3 en r€poso están se.pararlas20m. [l móvil A parta
2s despuris ¿le B y ambr» con aceler¿rcióne-s'di¿,3tnA'7 y.?.ml*
*:spectivarnente. hallar al cqho dá qué tiOmpri el mtivil A que va
retrasado logra alcirnzáritl mí¡vil B'l ,
a) 14s
rt) 15s
l¡BORl.!:lIA ñlt(!: 2.1
O¡r rnrivil parte ciel reposo con 4m¡s2 ¿,<:n qué segundo de su.
nr(¡virnien lo recr¡ni<i il()m?
¿r)n 2 h) n 4 e) n-5
dln,7 eln 6 ..,..',i
j'!
§'tl{}Blltr1trit ñIt(t: 2;-:
tln Fx¡mtre {ie rnueve con tlnit rapi<J<:z txrnstante rie iir¡/s tras un auro
t¡ue se encuentrit en reposo. pero crt;:ndo est¿i a iim el auÍo parte con
u¡ra ¿rceleracitin de ?.mls¿, h;illar it parlir tle esc molnt:lrlo cl liempo
en que log¡ra alcanzar al aulo (tiempo mÍrrirno).
a) 2s b) íJs t:) 4s
d) Iis e) fis
Plt{}$l,lli}lrt itlñ{}: 2{i
Ul irt¡tr¡ sale clel repex;o. [:n el once¡w¡¡ segurldo re.cx»re 47-m ittlt¡é
rlisri:ncia reco{rc errke los inst¡rntes 6 y 8 se1¡untlos'¿
PB()lltr.lirll;l tlllt!: B7
l.a trxlsícir»r de una parlíctil¿l (lll('r se firueve a lo li-rrgtr del cie X erstír
rlatJa ;xn: xfl) :lt. 1 4r¿, hallar su vr:l<¡cicla¡l an el itrsl¿rntt¿ t 2s.
;r) :i6 ru
<i) li2 m
a) 2i) rt¡is
<i) llirnls
a)80m
d) fili nr
P$OllHa¡In N§{l: 2t}
(-in móvil qr.re lierxr Mll(JV rec<¡n"e d tnalros pirrliqndc¡ del repos«r
duranle ciefio Liempo t. ¡:irrr luego recoff.er l¡00rrr más durante k¡s 10
seg¡undos si¡¡uienlers loo¡ando triplic;rr su n4ridcz. hallar d.
c) 7li m
llbícanos en Ia At). De la Culturul0l 6 {frente a la UNSAAC)
c) 9s
.-- . ACADEMIA GALTLEO
PIIOBI,IIHA Ñtr.{h 2TI
Un ¿ruto parte del reposo y sc rnueve cen una aceler¿ción constante
<le llunl* y viaja.durante 4s. Durante los préximos lOs se mua{re á
velocid;¡d con¡itant€. Se a¡rlica kx fren<x y el aulo desacel€ra a ra¿én
de 8mls2 hasta que §€ detiene. «:¿¡lcular la disfancia total reewrida.
c) 2ffi m
rru)BltrllA NR{h 3{l
tJn cuerpo l¿uuado vertiealmente hacia ¿rriba regresa al cabo de 6s al
punto cle l¿¡n¡r¿rmierito. I'lallar las wrlores de l¿¡ velocidad inicial y la
nráxima ¿dfura ahanzada (g, 1&nls2i
a) ll0 rn/s y 45 m tr) 20 m/s y 30 m c) 10 mls y !5 m
d) t5nr/sy20m a) 20m/sy l0m
Iln{Nlllj]lA NIt(]: Íll
I)r¿sde ciert¿r ¿rhur¿r se sueh¿¡ un;r piedra, hallar su velocidad al.flnalizar
el cuado segundo (¡¡ i0 mls¿)
a) 200 m
d) 206 rn
a) 30 mis
d) 10 mis
a) 400 rl
<i) 600 m
b) 280 rr
e) 210 m
b) 40 r'rv's
e) li nr/s
b) 300 m c) 100 m
e) 200 rl
b)6s
e) 13s
b) 125 nr
e) 120 nr
PB()llUtUA NIt0: i!2
i)csde lo altt¡ de un edificit¡ se lanza un¿r piedra verticalrne¡te hacia
drriba con velocid¿rd inici¿¡l de 20m/s. l.a pietlra llega a tierra 1Os
des¡:uús. I lall¡rr la altur¿r del edificio (g , , l0 m/sr)
c) 20 m/s
c) lis
P ft 0!![IIi]lA: tAIr$: il 3
Sc deja caer un cuelpo y se <;t:sérva que luc5¡o de 4s se encuenka a
Zom del piso l.desde qué altuiü se soltó? (g i 0 mA'9)
a)200m l6)30t) rn c):100 nr
d) 4001m ,,_,..¡.r..,4)l5ffi m '
,:.
i: ir:1:i.:-,.1: ,:.:.: iliil:]; .:tr
PIIOBIJIIIA Nlt0: !14
Se lani¿:;úna:,'pekrta desrle !;r superfr.eie terrestrc c(in una rapidez
inici¿rl de 50mis. Si después de un l.iemptl "f" ge encuentra
acercán<{c¡sc ;r ticrrzr co¡r r¡¡ra velocidarl de 30m/s, harllar "t" (g ,.
lQpr¡s'i
4I8 s
d) 4s
ITRORIJiIIA Nll$: l|í¡
A y I3 son punlos strbnl la misma veftical. A está 100m sobre B.
I)esde A se dej¿r caer una txrlii¿¡ y sirnultáneamente se lan¿a hacia
anib¿¡ olra t:olílá.cc,rn'rapidez de li0mls desde ll r,A qué altura sobre ll
chrr¿rriirn ¿¡mbas holitas'? (q ' . l0m/s2)
c)50ma) 8Om b)60m
d)90m- e)70m
Plt(lllilItl¡t NB(t: illt
Unrcuerpo ha sido soltado y rccoffe ¿n sus tres primeros se¡¡undos
igual distrnci;r que en el tiltinro se¡¡undo. l-lallar ia altura do la caída
(o.,. 10nr/s2)
a)90m
d) i15 m
c) i00m
Pll{}IIltiitl¡l NII(]: ll7
l)os cuerpos A y 13 se nncuenlr¿rrr a u¡ra misr¡ra aliura de 320m, se
deia caer el cuerpo A y 3s después se lanza el cuerpo Il verticalmente
h¿ci¿r abaio r,con qrÉ rapidez se lanzó B par¿r qu€ ambos cue¡ros
llcr¡ut:n al ¡¡risrno instante a tierra? (g '., 10mis'?)
a) 40 rrris b) 139 ms c) 42 nVs
d) 38 mis e) 41 nr/s
PB0AUIIIA ñR(): illl
(Jn gkltro aerostrtico se r¿lev¿r coll una ra¡ridez constante de 5m/s.
Cuando se encuentra a una ¿iliura de 360m se deja caer una piedm.
t-{allar el tienrpo que tarda ltr piedra en lle¡¡ar a tierra (g ., 10 mlsz)
b) 3s
e) 4s
a) 6s
d) 5s](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-46-320.jpg)
![r +r5¡w
pRoBlliua Istt{}t llf} .,ri :'' 'tqirr. rr .1-}:ifr:rr{"
l)esde La
¡:p¡tfi8-*riÉÜiidi de r¡nat iorr€ s{¿ 'ltrnztr una piedra
" v¿d'ic¡ihn¿nld'l*ió'iarr arfíba ccjn üna raqridez lriicial de 2.Onli i,a qué
disl¿rnci¿r del puntti de lanzamir:nto §e tzncontrará;luego de 7s? {g .,
10 r¡/sz)
a) 100 m
d) 105 m
PBffilüil¡tl{*0: 4{}
Detéf¡nine ét valdr de [a distancia d a [á cual llega un proye¡til qu€ es
lanzado desde el punlo A con uná velociclad de 15 m/s, formando
90" con el plano inclinado ert 30" respecto á la horizoirtai. (S¡ * fO
r n/sz)
B
a)30m b)40m
d)35m e)20m
lrllOBLlllIA NII()I,ll
c)25m
Dr:terminar la velocidad del mévil al cabo de 8s, si parte del reposo.,
a(rrvs
PB0ll[I]ilÁ Nlt(r: 44
¿Cuál es la rapidez (en rn/s) en el instante t -,, 8s, si e1 inrivil párte <iel
re¡roso?
x(m)
a) 1 m/s b) 2 m/s
b)200 m c) 300m
e) 108 m
e1?,00 p
d) 1300 m
p) 1000 m
e) IlJ rn
d) 3 m/s e) 4 rrvs
-:,:..,,ilr
,_.
PIIOBLIIIIA NB0: 45 "
l)os móviles A rg.l
B pali¡bn riel rnisrfro punto l,en qué instante se
áncontraran? .r .
jl , ",,'
c) t/z mls
:l:':i:+a. lÍl::
tt:l',.t+;:+..,
t( s)
t(s)
68
b) 10s
e) 16s
Plrl}BUilÍA Nttl]: 42
Deterfirinár' tá posición del
a)32m
b)35m
c)36m
d)30m
e)31m
, ,x(
trtto!il,r,uA NBI): 4il
Si en t ., 0s x,., 0m ácuál es la posición iet 'móviLen e[ lnstante
l'.20s?''_ . i
'V?,i,rs)
c) 15s
PRI}BLEIIA NRtl: 4B
§i laederatas& 2 segundos en ir de A hasta B. Determine el módulo
&hwloeidadrnBdia, siAC .. BC .= 6m.
Rpta:V=3m/s
PROBI,EIIA NRO: 4?
Un atleta escala una montaña en forma de triángulo de 3 Km de
lado. Si a[ subir MN emplea 4 horas y al bajar NP t hora. Determine
en m/s, la velocidatl media y la rapidez media.
MP
Bpta:V," .. 1i6 m/s ; V =, 1/3 m/s
¡{t ,Tignes sl P'otpqciql llqspttg§ Ia E Ws,riqqcig."! .,
4 16 8;
.l.l
i,r-. d 12 s
fj,:ffis.
a) 15 m/s
d) 13 m/s
Lr) 14 m/s
el 72 mls
t(s)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-47-320.jpg)
![-PIt{lBlJiU^ ñRl):,lll
f)<rs mí>viles parten sirnultáneamente de una misma posición en el
mism<¡ sentido para ieconer una dlstancia de 1600 m de jonl¡ilud. Si
el que tiene una rapiclez de 16 rnis logra una vcrnt4ja de 400 m. ¿Cuál
es la r;rpirlez tlel ol.ro?
Rpta:V , 12 mls
PBOBLII]H^ ñB(]: df]
(Jn hornbre v¿i carninando con unil velocidacl constante "V" y pasa
junto ¿r un poste tle all.ura I l. calcul¿lr la velocidad con qu¿ la sombra
d<¿l honrbre s¿ rnueve respecto del poste sabir:nclo que lzr allur;r del
hombrc es h:
Rpra: v., yf
-ll-ltri h)
PR0BLüIiA ñBl): ill
[Jn observador ve relarnpaguear un fty() st¡trre la cima de un¿r
montaña. Al cab<l de n segundos oye el trueno producido por dicho
rayo;rl caer. l,A qué distrncia de [a persona c'ae el rzryo?
(l ' , Velocidad de la luz --..'
V" . - Velocidad del sonido .r.
,,- '
!
:
nVsC.!
Rpk:d -';ñ
FB0ltHi[IA Nll0: lil ::
I)os perconas se dirigen de "A" h¿rcia 'lB;; .in olfAr.¿urne-pte, si la ruta
Ali es cle 30 Km. uno de elk¡s rectrne 1 Km mas án cada h.rra,
lleqando una hora anles que su arnigo al punto B; áQué furnpo eu
PR0BLIIMA NR0: 52 I ,: , :. i
A partir del inst¿¡nt<¿ mostr¿rclo. l.Qué distáncia csja¡án sEpüadbs el
mí¡vil A con el móvil IJ cu¿rndo éste' alcanza al m.óv*,:.:C;',I,jas
veloci<l,rdes conslanles de A. B g C son 2, fi y 5 m/s
respecl.ivamente?.
-.-+ ----'
lollBlód ó(J
I ll -*--.-:**lI t¡r () ¡l'1 RPta:d': 21 m
PR(ll¡LllIIA Nrt0: 5il
linconlrar el tiempo empleado por r.u) proyecl.il en lleqar a su
obietivr¡. si ¡rara un otrservador ¡:egado ;r esle¡ larda';rpiirenlemente 3
s
V ii4() m/s
Vn,", 280 nr/s
Rpta:tn , 17 s
Plt(ll¡LllllÁ .B(l: ii4
(Jna ¡:ar-líctrla en movimiento rectilíneo uniforme, en el inslante t. 2s
se cncuenlr¿l en el punto (5,0,7) m y en t,,lis en el punto (14,9,16)nr.
I)elermine el vectrir unit¿rrio de l¿r vel<¡cid¿¡<l rnedia para dicho
interv¿rlo de liempll y el vect<:r posición para t ' 1s.
Rpla:
,. J¡._. . .=- ._.
, .i f ; ¡ k); r'--7i .3 j 4k
PttOBL¡ilIA NIiO: 55
l)<>s ¡nóviles viajan en lr;ryeclorias rectilíneas cr¡n velocid¿¡des
const¿rntes. Si parten en el mismo insttrnle, uno del punto A, ,(20,0,0)
h¿rcia el punto fJ, (0,60,40)rn t'orr r;r¡ri<1ez Jl-4", /.s y el otro va
de Il h¿¡cia A con un¿¡ rapklez rie :Jl+or/.s. Determine el
tietnpo neceszrrio p;rrzr que atnl¡<ts se encuenhen.
Rpta:l, 5s
Ubícanos en la Av. De lo Cultura1016 (frente a la IINSAAC)
RPta:t = §5.
ITftOSL§*A N§{}: !i6
Un foco se encuenlr¿r a una ¿rltura [{ y en la misma v€rtici¡l qug un
hombre,de aiiura "h''. si esle avanza con una velocidad "v". iCon
qué velocidad avanza su sombra?
tsB{}Blfl¡§¡r NR& 57
$i el mo«iui1.o av¿lnz¿t a Lrr:¡r vei<¡r:idad constante, iCor que regider
avanza su sornbra proyectar.lzr en cl pisr:? Vn*oqd*,,,. *tfl
.' ,':r Rpta:V1 =Zm/syvz=6¡ry's
:: '
P.AOBIr*:M/I NHO: G0
Considerando idénticos los vagones de un.tren, al cruzar un puente
se observa que un vagón cruza el puente en 5 s. y 2 vagones juntos
lo hacen en 7s. ái:n cuanto tiempo cruza¡án el puente 3 vagones
juntos si el tren marcha a il6 Km/h?
llpta: t = 9c.
PIlOIlLli]l¿l NIt(l: (iI
[Jna persona parte de A con una velocidad de 1m/s hacia B. cinco
minutos después parte otra persona también de A hacia B con una
velocklad de 3m/s llegando a B, cinco minutos antes qu€ la primera
persona cQué espacio hay entre A y Il?
BPta:e¡r = 9${)sr
PIt0llLlJlIrt Ntt(): (i2
Un ciclista se desplarza en una pista rectilínea y pasa lrente a un poste
con un¿l rapidez constante de Snr/s, si luego de l0segundos pasa
lrenie al poste un autorní¡vil con una rapidez constante de 15m/s y en
l¿¡ misrna direcckin que el ciclista.
Delermine luego <le cuánto tiempo el ¿rutomóvil alcanza al ciclista.
( u )
RPta: V, . ,r[rñJ
' RPte:V' = 4Ñ/¡
FR$IrLHürr rYB$: Sfl
n"l.avas.-{ §j§al de !a ü-eniana de un tren un pasaiero ve caer las
Sotas &:BiváiryFralelámánte a la diagonal de la wntana. Si el a¡rcho
de ldüer,ü¡iriaes 4 veces la allura.
¿C6,É!
"nli;ii@@¿$Un
reatn*nte [m gotas, si no hay vkrnto y el
trai*e rlesplaza con qna wlocidad,d,e 54Kmlh?
lH ¡1'r
8Pta:v'=éx§§r+
PE0tt[§uf Nn0: i§
D<»,;'inj# +;B'se <lesplaz:m con velqei{ladát.eonstantes cuya
relaaiÚ:Éi;.*.',: á 3. si.a parlir de la poaiéión mo*gda, la met¡or
separarCilü' lre ambos es de 12 mehrx; y esto octint al cabo de 2
se¡¡un&s. Deter.rnine las velocidadÉé de ambos.,ffir&iles.](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-48-320.jpg)
![a -rffi,.,..
Árademía G*trlte*
-d,* ¿*ti.¿
pmg.fllA il§th li:|
Dos trenes, cada uno con velocidad de 50 lh/h, se dirigen uno
contra otro sobre la mismar vía, trn águila, con velocidad constante de
10m/s parte de un tren, cuando el otro se encuentra a 2{X}Km. y
dirigiéndose hacia el oho, lo toca e inmediatamente regresa arl
primero y mí sucesivamente, iCuánto tiempo vuela y qué distancia
recorre el águila hasta que los trenes choquen?
fipta:d = 7f Km.
PnonBfl,{ ItB& s¿
Una paní<:ula re mueve con M.R.(J. en el plano XY con velocida<.I dc
4mis sabiendo que e[ vector posick'rn describe un área <1e l2m2 en
cada seg¡undo, determine la distancia mínima que se acerca al orig€n
de c<¡ordenadas.
Rpta:d*," = 6 ¡¡
G;rupo §r¡Jl,.lo
PBOI}L§}Iil NRft Ct}
t-ln móvil efectúa un M.R.U., partiendo desde el punto A y en 0.5
segundos. llega al punb B- l-Iall¿x el valor d,e Ia velocidad rr¡edia en
el tramo AB-
17,§m
l0m
F*OXiltA il*O: ?{}
1..l.|..ril
if{,*:V*8§dt
Una persona sale del punto A €qauto a una vglocffirl ds 3é km/h
llega a B y desea regresar ceuninahdo a 4 km/h. $i l@ ct rccr¡rrido
duró 10h. iDuranfe qué tiempo estr¡¡¡o,§aminando?::'
t(s)
RPta:X = 1O m
PNOBI.DHA NIO: GB
Un móvil realiza un M.R.U. si en los 4 primeros segundos recorre 6m
mas que en el tercer segundo. Determine la rapidez del móvil.
Bp*a: t, = lfN¡
PR$til,tltA NB{}: f I
el instante méstradr¡,rel conductor del auto toca el claxon y la
.',rf:ir Rpta:V. = 17 mls
il
PBOBLEi{A NB(l: 72
Caminando sobre una escalera eléctrica en reposo, una penjona
consigue llegar en 40 segundos del primer al segundo piso de un
edificio. Si se mantuviera quieto sobre la escalera y ésta estuviera en
funcionamiento, tardaría 60 seguntlos. ZQué tiempo tardaría si es que
camina sobre la escalera mientras ést¿ se mantiene en movimiento?
RPta:t, = lzf 3
PBOBLEIIA NBO: 7l|
El tiempo que demoran en encontrarse dos aútos que viajan en
sentidos conkarios y separados itricialmente en 160 m es de. 2A
segundos. Si viajasen en el mismo sentido, el de rnayor velocidad
alcanzaría al oko en 80 segundos. Hallar [a velocidad de cada auto.
<-
RPta: v1 = 5m/s ; vz = 3rry's
Pf,tlüLEtlA NEO: 74
Dos móviles A y B están separados en 20 m, e[ móvil A parte en t ' '
0 s coh una rapidez V. ,.. 4rnls hacia el móvil B. El segundo móvil
:§.i!@ru escucha élieeo'cuando el auto se encuentra a [a mitad de su
ü'ffi*,<q"a veki|. ,iie.¡e.et g$¡móvil? V. -. 340 m/s
PttOBLll,lI.¡l NIIO: lif¡ ,r ,
Una persona lanza hor2ont¿ilmente una piedra hat,,r un, p§Éá
cornunicándolé una rapidez de 3m/s la pared se encuelllra a 15m del ,
punto de lanzamiento, a partir rle ese instante ¿l¡*.ftlo.de cuántoi:i
tiempo de haber lanzado [a piedra la persona escucl',:r¡i*:'ial sonido
originado en la pared?
M.R.U.)
V, ,.. 300r;'s (,,'u*.P!.-p
glX.
RPta: t, = 5,05 segum*oc
8x
PnOBLlJl{A Ntr(l: G{i . ril, i,:,r:
l-a sirena de una fábrica suena en forma con§hua düiant€ 9s un .
obrero se dirige liacia la fábrica en un autobris con -ona¡¡.¡QlSi rilt:
constante de 721*nlh iCuántq,...tjempo escüa'fiá diclii-¡ ot¡rei6;lü
sirena? _¡¡i :;ir=
-,,.,.,,*#l h = E,5 s.
PB0BLlilIrr NR(): 67
[]n el gráfico posicióriitiempo mostrado ¿it'Ia:,!¡ ra, determine la
posición X ene. InsfÁihte
t ,= 7s. :iii!Ír
parte en la misma dirección con v ::: Zmls e¡
instante e[ primero alcanza al segundo?
t .. 2s. áPara qué
Rpta:t=6s
Rpte:V = 2 ¡o/s
¡Tú Tienes el Potenciol. Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-49-320.jpg)
![r
rÍsr*Jr I
l,nt)IlllirllA Nll(h 7ir
l}rs móvilcs se despl;van en la misma pista con rapidez constante,
lur:qo de l0 s. el rnóvil A camtria su dirección en 180" manteniendo
r:onsf¿¡nte su raJridez. l,Qué tiempo emplearán en encontrarce desde
las posiciones indicadas?
AqAp§qH.qst&qp
80m
Rpta:vc > 12 m/s
Pll0ItLDlIA Nll0: {¡7
Fpta:t = I0seg.
{' ,@sf
a#;#!Sg'$}§ale oiroraéyil haci¿ A donde llegará después
,rrp;5¡gr.oüa
ar*affn
tu* * i'yan q a*r¡"¿r-dJ{o* r¡**po
r. §rl't .§,
,;óvil se desplaza con una v¿locidad cq.*$ñie de 50 mls]J'
a¡*ntts 40§ y lue.gei con una¡iifócidad csnstaúti{<te 25 mls durante
V.,',10 m/s.
3 _-*>
Vu,. 30 m/s
<-_o
60m
PROIILDtr|A i!¡Il(l: 116
'':.Un móvil A se desplaza con una velocidad de 30 mls se eneuentra
..iletras de un móvil B a una distancia de 50 rn, si la veheidad de B es
" 2A mls eDespués de que tiempo A estará 50 m delank de ts?
Dos móviles eslán separados por una distancia de 1000 rn v se
acercar¡ coL veloci{p{es conslantes de 20 mls y 30 mls
rcspiáctiv_a¡Bti.fjf,e- áQué asBácio recorre e[ móvil de mayor veloeidad,
"i,*t o.s.
. -01.1."o*,n",'.||'?1udosz00m?
upto." -- rro *:j- ie .
PE{}Bf.tlilA ItR(|: BS
ffi. ntosa,g.,&;''r$ff
1s0
km de fl sate un móül que demora 3
B9
;L.
se¡raración entre las montañ¿rs?
V, 340m/s.
PtlfIBtHlLr il80: sl
.r:igt:::t:t:: :
Bptn: [i'É¡fi-os m
un auto¡nouüista viajando a 40 km/h llegarfa a su destino a las 5
p.m.;'psro viqian<lo a 6O km/h llegaría a l:rs 3 p.m. Si de*ea llegar a
hu 4 p.rn. ¿A aup vptoqidqd tle.be vig¡iarlr, . ::. r : _ .
rmEffffil§nlh {t$ '.-,1.,
&qs lt.-d*.@s Sr V B Wxten simuftáneamente rlesde un mismo .pr-r+t¿,
«m u#eitlhdes mn#Rks de li y 8 m/s respectúamerqte en e{
r§iglÉ6,l¡taffi&. ,tdbs que ors direceiorres f(¡rqrran 60: entre sí LQuré
distansia&¡s q€para {ueg{¡. de 10 segtrndos?.
Bpfa:d = 70 m
P§OBt§illA ñll0: {t:t
Uo hrp rnide 15 rn y mar,cha a 90 km/h por una carretem paraleia a
{e ftif;a & un lwn. l,Cuántc liernpo errpleará eet¿ bus en pasar a un
tt*ar rls 8ffi m. qrrc viqia en cl ¡nbmc¡ senfido a rczón dc 54
§fiO
"
PIr0BI,ü[Irr N[0: {!,1
D¡ls rnóviles A. .
y B parte.n sirnultáneamente ct¡n velocidades
c(lnstante$ de 10 g 2{l m/s rcspectivarnente desde un mismr¡ pLrnto en
el lltismr¡ st:niirlu. A lfl(X) rn, en el rnislnt¡ instanle otro rnr'¡vil "C
s¿rle af encue¡itro <1e A y 13 en sániido opuesto con un¿¡ velociri¿¡d
constante de 130 rnl.s. áAl aabo de qué tiernpo el mévil "l!" equielistará
de los m<iviles A y C'?
RPta:t = 3O s
lJbícanos en la Ay.De la Cultura70.76 (frenle a la I?NSAAC)
los. Caltular el.valor <le la rapidez med¡¿.
"'''
'
PB{lBLlll}Itt Ntr{l-: $O
Dos móviles:Bárten simultáheamente de una ciudad A e.n el mi¡mo
senüdo es¡ velocidades d€ m Km/h y 60 Frrnlh llegan a una ciudad B
con urÍ.int¿rvalo dé 20'minutos. ¿Cuál es le distaneia entre las dos
ciudades?
,.:: :" R@:d = loo.km
PBOBI,$TA NR(h $I
il¡g pgiióna está ent¡e de¡s montañas que di.stan entre sí 2 Hrn, da un
griio''§..] ese¡¡eira los eeos prcducidos en ambas ¡maEtdas eon una
dif&dncia de tiernpos de 2"sefpndos. D¿iermine a q¡ré ástanoia eh
cada monrana se enconlrat¡a.
v, . 34O m/s
BFta: -x = 830 m
1'17O m
PnOBLli.U/t NIto: $2
[Jn automóvil se acerea hacia una pared a v ,- 10 rnls ctq. Si en un
determinado instar¡te el chofer fiace sonar la bocina V Cl Ca_bo de 10 s
escucha el eco. ealcular [a distaneia a la qqe se eneontrcha el rnóvil
de la pared cuando hizq sonar la boeina.
v.,,340m/sg
Rpta:d = 1750 m
Pll0llllill¿l NIUI: f)ll
Se desea ir de A hacia B y llegar a las 8:.00 a.m. Desplazándose a 10
rnls se llega a las B:10 a.m. y desplaándose a 15 m/s se llega a las
7:50 a.m. áCon qué velocidad se debe,desplazar para llegar a la hora
deseada?
Rpta:v = 12 m/s
l
-
soonr
---l
Rpta:t = 5s
PltlrllillllA NIt0: 7G
l)os nróviles parten simultáneamenle de un¿r ciudad A en el mismo
sentido y c<¡n velocidades de 50 y 60 Km/h. llegan ;r una ciutlad B
con un ir¡tewalo de 20 minutos. Calcular l¿¡ distancia entre las d<>s
ciudades
Rpta:e= lOOlgai
reela dirigiéndose a una o;r""..-li el
9o1dr9.gl9r.
toq¡."1a'bocirra v
escucha lueS¡o de 2s. l.A que distancia.rr.,.}¡at§! tgttocó la bocina
V, ,, l)40 mis .,, ,,=. .i .
i'
:,,,,.-." '.üpt* x
=,":-3.f'ItPBOIU,[rlI¡tNll0: zB .- ...::',, ., .J i.:
Dcx personas A y [3 eslán separtr<1a5. a una distancia
,,,d'. En c{erto
inlante A dispara una bala con una ve.locidad:de 170 m/s en
rlireccÍcin d¿l blanc<¡ que se encuentra junto a3i."§i.,8 escucha d
disparo y 3s. después percibe el impacto en el blanco. bete'nnin¿iel
valor de "d'r.
V" = 34O m/s
caminando a 6'km/h [ega 5 horas anLes.-?0,rn que
caminarpara flegar a las 12 a.m.?
PllIIBLIJilA ñlBlt: ll(l : l
(Jna persorra ubicada enlre dr¡s rnor¡lañas. emile un 1¡rito y recibe el
primer eco a los 3 segundos y el si1¡uienl.e a los 3,5 seg, ie.uál es Ia
Rpta: V,ieÉ4.
PR'f»tLültfA ñll(l: tl5
Un ciclista va con v '- c1e a lo.largo de la recta al pasar por el punto
O el; vistc¡ por un perro rrbic¡x1o en A que decide inierceptailo en el
punto B corriendo con vp '., 20 m/s const¿¡nte ¿Cuál tlebe ser la
vekrcid¿rd de ciclista para no ser alcanzad<i por el perro?.
PttllllHItA ilir1¡; 77 i:
t.lr¡ móvil que ltevá ¡n;' velocidad de 90 Krn/h se despli4»iir](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-50-320.jpg)
![7
lrt ¡ I 'r(ialíiel:
J#& /l,ca.cle§:ta
'J< * $'aada
*Y--"--.qt.''
PltOlll,liillit NltO: $d
GRUPO GJTI.ILEO
I)e "A" ¡r;rrlen tlos móvihs iraciá 'ilJ' con velocidirdes 5 m/s y ?O rnls
res¡:eciivuunentc. En él misrno;instante r1¿ "8" sale 'otto nróvil llacia
''A'i ..ru una velocidad de 3O mls, cru¿ánciose con lr¡s anterir¡res en
inlerv¿rlos de un minuto- iQué distancia tray enlre "A' y "8"?
Ilpta:d = 70OO m
PBOBIIIIA ÑlB¡h 9Í¡
'Ires móvil¿s A, I y C parten a las 8:00, 9:00 y 10$0 de la mañana
co,n vek)cidsdss dc ¡10, ttr5 y 5l l*n/h respectiuamente. Si van por la
misrna kE¡ecbria e igual srmtitln. ¿A quá hora B equidistará de
.]#-i:l
&&¡V* = §ffisqF"
pnotrxttm s
Una.particola *p. cB¡sA¡B «x¡ asskreicill eo'a§ta§te
su gráltcr & peükl6a X an furdán # tierr§s
muesfua en la §urc. freemrine al uelecdad inicial
aceleracién e$ !üJb2.
Xtr»
32
Pffi§¡fi*
Elmor*rhtb
Yt:?ml s
mwrh entagá&á&
S §*CI da 10 segwrdw h
Rpta:0: BZs
Pt(llllfiltrrtNl{{}: l(X)
Dos rn<iviles parten de,sde la ruism¡r posición sobre una trayectoria
redilí¡te¿r. cPara r¿ué inst¿)nic vt¡lver¿in a estar juntos?
Avc?
Rp*a:t = 90 h
P.SCIlS#üAilmA! 0P
fn el irsunm €n (F8 una seÉal de §árnito canrt¡ia a verde, un
autom&d s¿ F:a st mo/irnie$to csn una asek{a§i¡¡n de 1,8 rnl$'
En e¡ mismo id¡oe ma §n cm¡rirm «¡n veklrirlad ur¡lforme de 9
¡ís, en la miema &wr:kh del a*dot¡¡ÓI'il.
*A qué dt#nciaakarrze e! auto El *amión?
IIPta:d ='gOm
peüüL§&rffi 9f
Si la porici&r x {rÉ ¡¡§a parüeula es descrila por la relacién
¡,,--.§fz {-2& doode ¡ es,tá en msros y t *n segundoef'
entoncé$ su vokeidad rnd¡a anhe lm tnrtaahs t'"& y t"'4§, e8;
PBffi&ilIñ[illr l0l
Un aulo parte ds r€paso y
sigtienies ffh
finelme&te
pomedio de
hpta: t ,.24s
i iG. luego en los
kiiaa¿ alcarzada y
! en 10s más, hallar la velocidad
;,t nto
la udneided «r
ree<rw$esnqP#dp
t-{allarel vabr$d ár§& I
v(rn/s)
RPta:V, "'LSm / S
i ,,1¡,..
ffi¡*i"ilr,i
Un Sre se mü18$á'Un línea recta parte desde el reposo al
inicio de de una cdl€ e incremsnta su rapidez a razón
& 2 mls, En Ia segunda cuadra mantiene su
tercsra cuadra desacelera a razón de 2 mlsz
para tecorter las tres cuadrars, cada
Rpta:t .,, 25s
l§¡t
Alaá2 un canión que mantiene una velocidad uniforme de 30
l*§lh por un auto que en tal instiante llevab¿l una
de ¿lO t+r/h y una acekración conshñte de 8 th/h2, si 2h
el camién encuenta al auto malogado. dA qué hora se
cl autc?
Rpta: 15h 24:00 1,.4h
trffi¡§IAilB rO¿
Un súd iaicia su movimiento retardado con una velocidad inicial de
6e d*, §i b e§hrmcia dc espacios que reconió en el primer seguntlo
y d *§ino ¡egune de su moümiento'es de 48 m. iQué tiempo
Móea dc&rene?
np6; f -" §5
Pffir&16
Lh & * &¡ia en &edd desib una dh¡ra de 8O m y al rebotar
m d ÉÉro le &ra db hda la eu& parte d€ la altura anterior.
iÉ¡t* AsW?§ h¡r¡a¡ni*¡ hesta ryre se produce el tercer impacto?
S*t$r*''
RPta: f' '-' l Q'9
pffimil¡fn& ¡o8
lle un eaño ca€ una g$ta cada 0,1 se$¡ndo, ¡i cuando está por c;rer
la tereera gota se abre la llave 9 sale un ahorro de agua. áCon qué
velocidad dcbe salir dieho chorr<r para que dcance a la primera gota,
justo cuando llegue al pbo?
El caño se encuentra a una altura de 7,2 m y g-,.10 m/*.
Rpta:V,,.-.1,1¡nf S
?&l}lil,ElilA lt'trt): lO7
Un cohete es disparado verticahnente hacia arriha. Inici¿rlrnente sus
motores le imprimen una aceleraqién de 5 m/s2, durante 8s, y luego
se desplaza por acción de [a gravedad. ¿Hasta qué altura se elevó el
cohete? (g=10 m/s2.)
Bpta: H 240m
Sü¡¡CI=.kl
, ,,.-,, , ,.,- , nr, ,, ,, -fEI-l ¡TúTienesel1otencial.NosotroslqExpertencia,.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-51-320.jpg)
![rT§§CA I
';:{{;re1ffi:sia.!
ACADEMIA GALIL§O
Plt{}$LIIirIÁ Nll{l: I (}t}
Una pebh se sueil¿r dt¿sde Lrn¿ allura "h" y rebokr sucesivárnente en
el piso. l-.n r:arcl;r retroie pierde ia rnilad de su zrltltr¿1. I Iallarr el espacio
total quc recr¡rre ¿rr:tes de dr.¿tenerse.
Rpta Íl "3h
I,ll0BLtlilIA NIIO: l0f)
L.n cierto planeta se observa que un cuerpo cayendr> cerc¿r de la
superficie, en caíd¿r libre, duplica su velocidad luego de recorrer 81 m
en la que i¿:rda 3s. Calcul¡rr la aceleración de la gravedad en este
plan¿ta que no tiene atmósfen.
Rpta:.{ 6m f s?'
PltOIlLB,Vrr NB(l: I l{)
Si un cuerpo en caíd¿r libre desciende las ú¡ltinr¿rs ltes cuañ¿rs pitries
de su trayecioria en ur) lapso de lls. Del¡¿mline desde r¡ue ¿¡ltur¿r se
deió en libertarl.
H 180m
RPta: g= l$ ¡¡1t"2' '
PB()I¡L¡i,llA NIIO¡ I I I
Dr¿sde un gkrtxl que ¿lliciende a 5 m/s se lanza un objett-r con una ,
vgl<¡cidad de 5¡ris respecto del gbbr: fomtando un ffiülo de li3!
c<» la horizt¡ni¿rl. i.A qué allura l l ¡nedi<1a.b1b§i:li:.lagüperficie se lanzii
r¡l c¡bjeto. si ei ¿rlc¿rnt:c¿ llorizr¡nt¿ll loqr¿rdr¡ fue de.,tr1,.!,1rn? g .' lqsrl§'z
Iiptr: i/ ''.38m
I:l prcyeciii rnoslracftr se lanz,r con vi . l[JnVs y con un¿] inclinación de
ir0". ¿rl c¿¡t¡o de qué 1ir:m¡rr:. el ¡rroyetf il impacla en B.,g .,.'10mis2 ..
^ ,Rpta:ú ,'0,73"s'
t)n i,rroyeclii es l¿¡nz¿u.ir¡ desde "A" ccrn üna velocid¿id Vi= i0rn/s,
l<>rnr¡rncLr rnr ;ir''Lrlt, rlc l):J' c(rn l¿r horizr¡nt¿rl y se incrusta en e-l
¡runto 13 peq)ci.iriculannenle al pl;rnt¡ inclinado. Calcular d-l1iempci
rll l mo;imier l lr¡ rJtul ¡:royectil. q:r:'10 rn/s2
Itpta: ü' -',il(J,25
I¡¡¿OBI,I]}IA NBO: I 14
[Jna masa qgy pequeñer es lanzada hacia la part€ superior de.un
pláno inclinado corno'se mueská en la figura. ZCon'qué velocidad,
debe dejar e[ plano para lleg¡ar justo al punto Pl §"' 10 m/s2.
'
70m/s
J Vi-.lOrn/(
8m
16m
Ubícanos en la Av.,De ls Cularra7076.(frente a la UNSAAC)
Rpta:r = 16m
PnOBLnilA Nltl): I tii
Desde un glot» que ascir¿nde con una velocklad v,-6¡nls, se lanza
una piedrar horizontalmente (respe<;to del globo) con una velocidad
horizontal V-, .lim/s. [-a piedra ex¡:erimenkr un alcance he¡rizontal de
1l¡ rn h¿¡sla [e¡¡err a[ suelo. i,Desde qué altura I-l se lanzer [a piedra?
g... l0 m/s2.
Bpra: /{ ,-. f'/¡n
IIII0BLEMA NltO: t l{i
Un auto que p;rrte del reposo acelera a 2mlszdurante cierto tiempo.y
luel¡o desacelera a r¿zón de 3m/sz h¿sia detenersa. I-Iallar el espacio
total re¡corrido ¡:or el auto. si estuvr¡ 90 segundos en rnovimiento.
Ilpta:e = 486h.
PltOIlLlIüÁ Ntl(|: t l7
LJn móvil que pafl.e del reposo desde un punto "r1" comierua a
moverse en lÍnea recta con ¿rceleracicin c()nstante y despuás &
recotter 2 metros pasa por un punto. Si después de 2 segundos de
;haber ¡:asado por dicho punlo el m<ivil tiene una velocidad de 12m/s.
I-lallar la aceleración <iel móvil.
Rpta:a = 4 ny'oz
PItoll[UMA Nno: I t8
En el movimiento lineal de la figura
instanle t [a vekridad es nula?.
v"*-12,5m/s áen que
Rpta: f == 7§
PIIOBLIIilIA NllO: I l0
Un ómnibus se encuenlra tlelenido y hacia él corre un pasajero cer
velocidad cons1ante de Bm/s. i:n e[ instante en qu€ se hnlla a 32m. el
ómnitrtls, perrte con ¿rceler¿¡ción conslante moviénd<¡se en la mi.sma
d!¡ección y sentido que'el pasajero. I-i¿rllar.la rnáxima aceleración que
podr;i lener el <imniLrrls con l¿¡ condición de que el pasajero lo
alcanc¿.
:. Bpta:a = l¡qfu4
PItOllLIt]Iil Nlt0: I20'
I:l gráfico adjunto nbs presenta el movimiento de un móvil. éQrC
disla:ncia r.ecorrió en el'cu¿¡rto segundo de su movimiento?
R¡Éa:e" = f6¡
El gráfico y ,. "f(0, rncxtrado nos prescr*ci e[ movimiranb de 2
móviles A y B. Si ambos móviles s€ encuentran en p. eQué distancia
los separaba inicialmenLe?](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-52-320.jpg)
![r
: ,-,
¡tl#t'-
¡1*xi}**tx§:¡.
¡!*
üxl'?,§'**
lY"3'..:*
l',ñt{¡I}L¡i,!üA §!t(}: i2I
rljn nr(rvil se nluers ii io l;ir1¡r r.lt¿i ei¿r X.
'eul..1iern¡xr de ¡rcue¡do a l¡r qr¿ific;r <lutr
rielociclarl ¡nerdi,i r:rllre: r, t)s y r, 1 lis
r(r u,/s
s)
Rpta: I/. L,67m/ s
Pltolll,UilA NnO: l2Z
Un fen sale del Erato A cen una velocidad de Z5rnls a las O7
horas y detre llcgar a la ciudad B a las 12 h. si después <1e 2 h. de.
viaje un huayco lo detiene durante 2 h. ácon que veiocidad
cor¡st¿rnte <iebe retorr¡ar el viaie ¡rara lle¡¡ar a B a I¡r hor¿t
indic¿rda?
Rpta:7, 270km/h
IlltOBL¡lüA NII{}: l2ll
Un camión <1e carga de l! rn. de largo !/ que se mueve con M.R tl.V.
in1¡resa a un h.inel <le l]5 m. l)e largo tal cc¡mo se indica. Si sale
completamente «lel túnel con rapklez d¿ 16 m/s. Calcular el valor de
su aceleración.
4 m/s
lA---
ffiinm
,I:l'.:t in: :§
:: ,r¡i.,,]]..
iiri::f::,,r:.
' i'i:¡r:i:¡l:ri
. ,i ""+?. i". . .l lrI*ii: .-r lir¿!¡iÉ:t:.:!:!
Rpta: a el§i&?#
.
:
rtr.!i:.:: :
..*.;:,. -
dsi&
Si su vebcidacl varía co¡l
sc «ijunta, delemline su
Plt0lllliiUA ñl¡0: 12$
[Jn automovilista que se desplaza en línea recta a razón de 1Om/s, de
pronlo vé un bache a 35.¡rn rnás adelante. El tiempo de reacckin para
arplicar los frenos es 0,3s. después de k¡ cual se va detenienck¡
uniformemente en 5s. Determi¡te a qué distancia del bache queda en
reposo.
RPta: x = 7m
PltOBLllilIANll{}: llt(}
Ai apiicar los frenos ¿r un móvil, este desacelera uniformemente y
ret:sne 2-O m hasta detenerse. Si los últimos 5 r¡ la recorre en 1 s.
eQué velocidad tenía al momento de aplicarle los frenos?
Rpta:v = 2O m/s
,::?:i:,:::¡¡::.¡;ii}lr,,.-
Plt{lt¡LlttrIÁ NR{): MI .'uiil';':.':'¡::::l:::rj.-l il'.:r"
[Jn mí¡vil con movimiento retar:dadó pasa suü ente por dos
lramos contil¡uos e iguales cada r¡iio de 10 m de ffitud. El primer
lr¿.rnro lo recorre en 1 s y e[ segtt o en 2 s. aCalcufdJ el valor de la
vekrcidad al final d¿l se¡¡undo trarnt*?1,,.
.,,,*,d..
tr,i
l¡lt0llllliUrl ñIl0: Iil*::r'i.;',:'
eii"i$..,
1lo4§itud
de la pendiente.
llil.¡'¡:li]:-"
L)n móvil parle de&iáposo¡1r rncor.e una trayectoria recta de 270 m
dur¿rnle los tres piimero.$'lsegundos v$ con acelemción constante,
luel¡r con la veloe-:Éad ji trdquirida se anula la aceleración durante 6
segr.rndos más coñ,:fe$iaai comple.ta.§t recorrido. Hallar Ia aceleración
aet:.1',i,,,§¡mnte eFr
: Rpta :a = 12 Írsz:::|:-. ;1,,,,
PnOBLIIIiÍT1 F;r¡il:r -
,:Un móvil va c'óiiiifliB,i8 nto uniforme con una velocidad de 1O m/s,
,á.:entrar u un. ÉilHdÉnte atlquiere una acelemción de 0,4 mlsz si la
; de h pe4§iEnte es de 1 km. Calcular el üei'npo que demora
'fiift ,, = 5/3 rn/s
Bpta:t = 5O s
PB0BIü¡IA ñB(tr 124
Dos móvikls A y t3 que s€ sncuerltran sep:r.mdos una distancia "d",'
parten sirnultá.ireamente ,:n tifea recta con ace,lem{:idn€$de 10 m/d
y 6rnlse respeclivamenle. I la,ltar el valcrr ele "dll,ii- ctiando uno de
ellos ¿¡lc¿mz¿r al olro, el médulo de la <life¡encia i{e sus vdllrcidáides .qs.:
PNOBT,ffiNBO: Ifl,{
,lJn m§¡ril reeorre 4O m durante d tercer segundo de su movimiento y
iifir;¡rr' urante el quinto segundo. fHerm.inat su velocidad inicial si su
,üebláración es const¿rnte.
;t:' Bpta:vi = I5 ny's
dc 40 rn/s.
.-:
Plt0llf,tütlA NRO: I Zii
,i¡l.n g: d -;2oo'm.
tjn móvil s€ mueve a 48t&n./h en lfnea re,cta Se aplican lqs.frenos y
se detiene hrel¡o de rcrrl*rer m. Si se hu.§lriiá.estado máüi¿ñdo a 96
t&n./h y st: aplicaran'l,óo frenr¡s cr¡mo e&d$p. g=nterior, de manera
que se «:btuviese la:fnis¡na desaceleraeión. .Qq]iular la distancia que
reconerí¿r desde el.iñqnento que se aplican 16§.,1,, nos hasta que se
,t',,r, RPta:X"Sm
Itlt(llll.lilU¡l NIIO: 126' . "
I-a vel<¡cidacl de un mévü--qqa¡,ec.orm,;l,Jó0 rn. en lín<srecta e,s de
llti m/s. Si su aceleraciá¡'ü,pqrnst"Et¿:; i¡¡uat 0.7 nilf.'Gicular ta
vekrcidad de padi<la en nr/s.
Rpta: V, ,,, 34 mis
PnOBl,fiüA Nll0: 127
I)os m<iviles A y [1 se hallan el punto "0". el cual disia de 100 m. del
punto P, ambrx rnóviles ¡:arten simultáneamente del re¡roso *sde
"O" con [a misrna <lireoció¡ y sentido siendo sús aceleraciones de 4-y-
6 m/s2. ¿Al cabo de qué iiempo de partir equidistarán del punto P,
colineal conAylil?.
Rpta: t .,' 20 s
Plt0llLlirll¡t Nll0: I2ll
(ln peafón corre l¡ar:ia un ó¡nnibus para alcanzarlo con una
vekriclad d¿: 6 m/s («rnshnte), en cl inslante en que se encuentra a
2li rn por dct¡¿rs de dicho órnnibus. lln ese mismo instante el
órnnitrus parle del re.gwr, acelerando a ratón de lm/s?. Determine si
el peakin ¿rlc¿rnz¿r o no, al rimnibus.
Rpta:No alcanza al ómniLrus
PAOBLE,IIA NIIO: IBI
Un móvil lleva una ¡¡eloeidd de 35 ¡¡r/s y frena unilormemente
deteniéndose luego de reeor?er 5O m. iQué velocidad tenía 18 m
antes de llegar al reposo?
Rpta:vi = rs m/s
PIIOBLIIUA ñRO: Iil{i
Un móvil se mueve en línea recta con una velocidad cuya
dependencia con el tiempo se muesha en la figura. cQué distancia en
km rer:orre en las cuaho primeras horas?.
v( km/h)
Rpta:e = 320 km
PROI¡1¡itrlA NRO: lilT
Un móvil se desplaza con una velocidad de 60 kn/h aplica los frenos
de manera que desacelera unif<¡rmemente durante 12 segundos hasta
detenerse. La distancia que recotr€ en este tiempo es:
Rpta:e = l0O m
GRI.IPO GALILEO
, , TE-l ¡Tú TieneselPotencíol.ilosaÍ¡osla Exprlencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-53-320.jpg)
![risrca ¡
i;r.¡ñF+i!
'r'!á+,i'4'; ''".rr*
1:
ACADEMIA GALILEO ''1:
PBOIil,§ült ilBO: l:ltl
Dos rnóviles con movimiento rectilíneo incrementan sus velocidades
en 2 mls y 3 m/s, cada segundo. Si parten del reposo áEn qué tiernpo
cuadruplican la separación que lray entre ellos. cuando t.,,5 s?.
Rpta:t = 1O s
PB0BLlaü/r N[0: I3lf]
[-as velocidades <ie los automí¡viles A y lJ vari¿¡n r:on el iiem¡:o cie
acuerdo con k¡s g¡ráficos moslraclos. en i ,. 0, ¿rmtros d¿¿ encuenir¿rn
en el kilómetro cero. Calcul¿rr el espacio recorido por cada uno de los
móviles durante 02 horas.
v( kmlh)
ur:l :
.
Rpta: e{'*ifigt Éf¡ ; eB = $Ot<m
Lrn nred dasanolla M.R.U.V. haltará espacio r€¿ofiidó ,g¡'él ei¡árto .
seg.rndo de su moümi¿nto a partir del sigulenle gráfico. v ,- f(t¡.
d¡nl¡}
:¡1 :;i'' ,;i
§e tare¿ hacia aniba dos cuerpos co6 la misma veloeidad rnicial dá
100 m/s, después de cuánto tiempo se.encon'karán a la misir¡a altura
si uno de ellos si lanza 4 s de.spués de hat¡e¡ lan&do et pri {g ..
10 rnis2)
PA0BLBIIANBO: l4l I
Una esfem es lanzada verticalmente hacia arriba con ufti velociilqd,l:
de 50 m/s. Calcular e[ mínimo y máximo tiempo que 4¡¡pleq,'en
alcanzar la altun de 120 m. (g,= ¡t¡ 67tz¡
Rpta: tmín = 4 g ; {rná¡ = 6'.p.1
',,. ,.Í
PBOItlItilIA Ntr{t: 142
:¡):::1
-!;
Calcular la altura desde donde fue soltado irn otrjeto. Si en los dos
últirnos segundos recorrió 4O m. (g ,, , 10 m/s2)
Rpta:h=45m
t)ltOBLtiMA NBO: l4i|
f)eterminar la altura máxima de un objeto que al alcanzar la quinta
parte de dicha altura, posee la velocidad de 20 mls. (g..,10 m/s'z).
Rpta:h = 25 m
PROII[llllA NBO: l,l,l
Dos móviles parten de un mismo punto simullaneamente en la misma
dirección y sentido. El móvil A lo hace con una velocidad constante
de 20mls y el móvil B parte del reposo. Calcular la aceleración que
deberá tener el móvil B para alcanzar al otro en 10 segundos.
Rpta:a = 4 ¡tls?
Ubícanos en la Av. De la Cultura7076 (frente t lo UNSAAC)
Pll0ll[I]rtf¡l NIIO: 145
Un coche de carrera puede correr a 126 l&n/h. Si sc su¡rone que h
¿rcelerackln del coche es c<>nstante y que aicanza su wlocidad
máxirr¿t al cabo de 4 scgundos. I)etemine la distancia que recorrerá
a[ cabr¡ de 10 s. Si partió del roposo.
Rpta:d = 280 m.
Pk0lll,llllA NIIO: lzt{i
[Jn móvil parie del reposo con I{.R.[].V si durant¿ el onceavo
se¡¡undo recorrd 84 rnetros. l}:termine la distancia req<¡rrida entre los
inst¿rntes I,, 4s. Yt.,' 8s.
Hpta:X = 192 m.
PI¡OBLDUA Nll0: 147
[Jn rrróvil inicia su moürniento desde el reposo con una aceleracién
conslanle de 0.9 m/s2 y después dc un tiem¡lo desacelera a razón de
0.5 m/s2. Si i.odo el movimie¡rlo duró 7 minulos. Calcular el valor de
la velocidad n¡áxima que krgró alcanzar e[ nrírvil.
, Rpta:V = 135 m/s
irttuil,tstta Nt!O: IdIf
Un móvil parte del rcposer y alcanza una velocidad de 5 mls a[ final
de 4s, luego prosigue con la misma velocidad los siguientes 4
se.<¡undos. I:n este punlo choca frontalm-ente con una pared que le
invieric su velocidad en 180', luego de lo cual se detiene en los
rlltimos dos segundos de su movimiento. Calcular el valor del
desplazamiér,rio total'del, móvil.
Rpta:d = 25 m
;;i{é.-:100 m:?
Rpta;t = 5 s.
' ,;iir.:)nii:rrr:.: :' ,
PBell"*§Iü,il'.#tfi¡ laf) I ,,' ,.
Un:*ailiant¿: pa¡a:::gng.dir la.;'al.tura i3q un árbol, lanza untr piedra
{@!i;r:na distfl.nGiar¡i bnzental de 42 m. Mediante un aparato desde
.,!ij lo con g$,,ffffio de ele.vacón de 53'. Si él constata que el
trÉffi#Jransüiililcld;iáAlrn a di§parq,.y la lles¡ada de la piedra a [a
g:ñP del á¡óo[ es t'C 3 seguhdos Calcular el valor de la altura del
'riiiiiiiffi", . Rpta:H = rr m
Ptl0t¡LBtr[il iln0: t5(,
f)os cue¡pos con velocidades iniciales oJiuestas d¿ 1O mis se rnueven
a lo.lilrgo de.la misma lire¿ vertical. ¿Al cabo de qué tiernpo se
,.ie.rconÍia'ián, si en el instan'te inicial están Separados en una distancia
:_.
PBOllI,ülIArItr&, l5l .'..
Deteitni¡#r'Ia vetoeidad rrerlia en el intervalo de tiernpo de t = 0s.
hmta;'r o-= 3s,de'ii,n.sróvi[ en caída libre, si fue alcaneado con una
v..cidadlriie,Ai.de 10 j rr,r/s.
s =' [0 ml*
Rpta:7m:--S jm/x
;,P-E0I}I,IIIIA NII(I: I ¡52
.,Ün paracaidista se deja caer desde una altura H y al cabo de cierto
tiempo abre sus paracaídas e[ cual produce una aceleración neta de ,
2 j ml* si clespués de 7 s. cae a[ mar con una rapidez cle 46 m/s.
Determine el valor de l{. g .', 10m/s2
RPÍa: e'¡' = 324.2 rn
PBOIILüI|A NRO: lSil
A través de una renclija una persona ve pasar un cuerpo hacía a¡riba
y lue¡¡o de 3s lo ve ppsar hacitr abajo. Si [a rendija está a una altura
de 20 m. sobre el suelo. Deterrnine la velocidad con que e[ cuerpo fué
lanzado desde el piso. (g ." 10 mis2).
RPta:V, = 25 mfu
Plt0Bt llllA Nll0: l5,l
Se lanza un proyectil con vel<¡cidad inicial v ., 90 m/s y ángulo de
elevación de 60'contra un plano inclinado que hace un áng¡ulo de
30'con la horizontal. Calcular e[ valor de alcance PQ. (g ,., 10 mlsz).](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-54-320.jpg)
![r
:,
,ds 6* i(.:;1 r[ L:{ }1 i ¡__1 {,i-¡r{Í{ed **- ¡il
{'t:
,sá¿. 6rnt¿{¿
-s11'::i--** .
Rpia: l, ,. .54() rr
ltItO¡lLIlMll Nll0: I ¡-r5
i.a 1lrlrfir:ar r-r]ueslr¿r l;¡ v¿rriackin dr¿ I¿r vek>cidad de unn pelola latrzada
'rx¿rlir:¿ilrrir:nie haci;r arrit¡¿r desde la ¿rzcle¿r de t¡n edilicio de l10m de
;lllura. (lalcul¿lr el lierrnpo rtruc <lemorar en lleg¡ar al piso.
v,r/,
20
RPta: t = l0s.
Pit{}HL!}li¡Á NIIO: I5(i
iina b<»nb¿r l¿rnz¿rci;r destle un ¿rvi<in que via;a a I]00 ¡n/s. irr'4lacta
:vrbre. un barc<r én rep()so (:on una rapklez rie 5($ m/s. Caicule.r.pl
ii.rn1po, qu€ {arda l¡r bornl¡a en hacer irnpacto.
{a 10 rn/szt
§,[t{}§Lii}*.,t iiJll{}: I i¡7
Spta:t a 4Os.
GSttrPo Gtu-rLEü
Pltl)Ill,lrllÁ ItlE(): llill
[Jna partícula se lanza con una velocid;rd init:i¿ii de 20 mis haciendo
un án.r¡ulo de liÍl'con l¿r horizonl¿rl. f'lallar al cat¡o de qué tiernpo ei
vtuctor veiocidad form¿rrll un án.c¡ulo <le 3'/" con la horizontal.
(g¡.,i0m/s2)
Ilpta:t = O,7 s
Plt0l|illllA NIIO: l6,t
Sobre un suelo horiz<¡ntal se dispara un proyectil con vi'=20i '1- 30j en
mis. Calcular en metros l¿r rnitad del alcance del proyectil. Considerar
(r l0m/s2.
. - ¡:-:,rir,'' ,1 I 1,.r,3P1.,P = 60 m
.
PIiOIILEHA NIt(l: l6i"¡
Un proyectil es lar¿ado desde el ¡$o (0,O) metros, y,alcanza su altura
máxima en el punto (30,20)rn- (láffialar: ¡
::-:+-lii=,,,,. ..,
a. Éil án-*¡ulo rle lanza¡{¡i.ü¡.rto O.+'.].:.,:
b. l¿ veiocidad de larx+lmiento v,
angulo?.'{h{r4$mls' }
,i...rij,ii:.:..}.i:,
,:.:r.::u:ri
',. (g=10 m/sz)
Rpta:vi = 25 m/s
Rpta:v = 20 rn/s
PI¡OBIJIilA NTIO: IG[3
ur[€üe.t.?Á) es lanzadp,' !{ lliiente desde una altura de 7,2 m con
una ú¡-,[6;¡¡/5 '.f-oiil-:&1ürü biidad choc¿r con él pisó y báio t1ué
1)esde un qiotlo irrosláiic() qne se elev¿r vedicalrnénte con una
v,,irj,:iclai] de 20 lnis. se ¡,¡tranrlon;¡ una carfla en el inst¿rnteén,qug el
elot,o se e¿nt:uentr¿r a 16(J L¡r sot¡r<: el sueh. I)et€tmine el tierrp,gilq:¡
t¡tie ile<¡at:zi a lierra [¿r c;r*,ar' (g' 'i,r,ls2)
,..,BBt
't = B;
",
[Jn cu<.rrpo en caí<la litrr¿¿ re«¡r're la prirnera npita<i,ác.su ttus-qf*t¡r*"
en un seg¡undo. r,Fin que tier¡¡:q:,ré:ca¡'rerá lr¡ tray*p-toria:eompl¿Éa?.
" BPla:t =r:tr'41 3
t::
Se,<le.ia caer un cue¡po <lest1e un¿r altu¡a de.4{,rI. mehos con gafda
lit;rre. I-a disi¿rncia ,Iqp r".orru el cuerpo €n ;triúffi ii s€gur¡do es:
.,:l
.:- Rpta:h = 24,5 rn
Irlt0lil,$lIÁ NIl0: lSl)
[)n cuerpo clemor¿r 4,1,ise§ ea ¿llcanzar.,]#,:f¡liitad de la h,*,, Deterrnine
el l.iemp<: t¡ue esluvo erri(t1.,+t+',,r ,,..tr-'
t' ''' /$'JcRBta:
PII{IBIII}IA NIt{l: l(il
Un proyectil lanzado desde e[ piso con un ángulo de.elevaeión de 74"
demora en llegar a su punlo más alt¡r 4 seg" fIallar Ia altur¿r ¡*óxir¡ra
alcanzada. (g, lom/s')
Rpia:h = go m
Pit{}$Lllltlrt NIt(}: lG2
l."ln ¡:royeclil se -l¿rnza con un¿r inclinaciótt de 45" y llega a una
disi¡rx:i¿r dt:4 l«n. (l¿ik:ular la velocid¿¡d inicial, el tiempo en elareg
la ¿ritur¡r m¿ixima. (g 10rn/s2) :
, l0()nr '. ,,, 2tt/ls . h,n l(Xp¡Kpta: ' ;
PII{lBLliillt ñll0: l(i7
iiá*iá,rl¡u alfura''de Il,2 rn un cuerpo se lanza horizontalmente con
",
,O m7s..a:C,o qué velockla«i en m/s ll€gará al piso?
::i" Rr¡..ta:v = 10 rn/s
+t¡0$f,llllA NIr0: lGtl
Di e A se lanza un proyectil con dirección al punto P. i.Cuál debe
sér [a v¿locidad inicial p;rra t¡ue el proyectil impacte en el punto f3?
.- li
Rpta: ,¡ _ ..n " rn / s
2'
PROSI,IñIA ñlt0: l§9
Un proyecül es lanzado con un¿l velocidad inicial de 10 m/s que hace
un.ángulo de 60' con la horizonlr¡I, contra un plano inclinado que
forma 3ff con [a horizontal. tlallar el alcance sobre el plano
inclinado {g''10m/s2)
Rpta:d = 6,67 m
PROBI,IIilIA NltO: 170
Se dispara un proyecti{ con un ángulo de 37" el cual choca con una
pared vertical separada en 400 m y a 775 m por encima dei nivel
donde parte e[ progectil. Calcular su veiocidad inicial. (g= 10 m/s2)
Rpta: v¡ = 100rn/s
15m
¡Ttú Tienes el Poteneio.l. Nasatras lq trixperiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-55-320.jpg)
![I
§'t§§*e §
Este movirniento se pro<luce cuan<lo sobre un cuerpo en movimiento,
actúa una fúeza perpendicular a la dir:eccií¡n del movirniento y a esta
fueza responsable de las curvaturas sr: le tienornina iuerz;r centrípeta.
Si la mag¡nítud de la fuerza centrípeta es r:orrstante, entonces el r¿¡dk¡
de la trayectoria es constante.
PERIODd (T). I-.s el tiempo que denror¿; un n¡tivil en dar una vuelt¿r
complela.
... Íieiltz¡ totdl
iltililCn) t/r' I ttellds
FRECUENCIA. (f). l-s Ia inversa del período, que representa el
número de vueltas que realiza el móvil en una unidad da tiempo.
!,,,, 9l:g* -!:*': y!!-11
ticnlpo total
-i lti"rtt, ,')
7t
S=Re
Il:Radio<lelatrayectoria(m,cm) ..,''',,1
0: Ang¡ulo central o de.splazamiento angular,,(iád)reryfgrado§)r :
+ltr::"'::
n-..a
VELOCIDAD I,INEAI- O TANGENCIAL. , .
0014' :- (rad/sl. v.R:-..Ru,
/.-t
2n
t4 ZnI
1',
,,.i''
ACELF:H,ACIÓN TANGENCIAL (aJ. Magnitud física veeto -Hfióuá
expresa los cambios de móduk¡ que experimenta la.."t9'heHad
tanl¡encial. i'1,
. ,1,¡,
l', l1 t 1 )
Lt, -.:..-- .. lm / .t . r'nr / s )
Í'
q *, *-J
(rud t s,l .1' u, , Ra
f''
ACELERACIÓN ANGULAB (cr). Fi aquel vector que se manifiesta
en el centro de la circunf¿rencia, que. nos expresa la rapidez con la
cual un móvil c¿rmt¡ia la velocidad anqular.
SROy': :. :
1f
VF]LOCIDAD ANGTJI-AR
Ílbíconoi en [a Av. De ld culwra7076 {frente a h aNSAAC)
Moviyniento
effpqlvrlA GAI,Itpo
MOVIMIENTO CIRC{JIAR UNIIjORME (M.C.U.) Li rrayectoria
es una circunferencia.
00l-C/(':> l/,..U il'-- I. -
I t1)
w:f,Cle..> U-:(l 0.-ttt
^,.-?!t,r
MovIMIENTo t',1t',Lfr[.1il:l:iRMEMENTE VARIADo
y;,.y¿¡[¿l¡ls-,¿,,.,ste
'"'',¡y.= y¿¡i¿g lq =.>cr
.- s1¿
L-n iguales intervalos de tienrpo los cambios de velocidad tangencial y
angular en m<icluk¡, son i¡¿uales
B=f 't:l),.2 )
0." - tt. ¡]-a(?-tt- l
2
,l
U =}ut l:-.dt'
'2.
tt,,1 '= t+,,2 *,2a0
0
2r
¡ ,=,¡¡l¡¡¿¡6 de vueltas.
: :i:.;.
4., :
AC ELERACION C ENTRIPETA :
l
n^-.u {rrt,s', rrrr,sl)
:-R
,u
a, -,1 lnl .r'. ttttl s- |
I
ACET.EBI€IÓFTI TOTAL:
221fl -=a +a'lcl
I
.l
t-, Lü i
, */;;-,¿
I -Á ,:r,t-¿ ü-.
Lt
-, "'
'¡
-tÚ.,&
' . t.
L
tj "'
ii.,l..
,11l'i "](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-56-320.jpg)
![7
,;NÁ,,W &a,aeleax i a {,i *-lj i"at:
=:-:l-:-
o/5''4
'.'¡ /, ,.:.(
tr;tflffii
| ., !¡/
i *-!
G§TUP{} GA,T.ILEO
P'itriliii,li;!lr't }'iNii: (! I
i)l;s i:t;l-lículas riul¡lrr qilLllrill''Iroirlil{:niír ¡it' los t,'l1l<'' lt.s tit' tlt,
(:li¡rnl{rro 1t13'y crl l<¡:; sc¡ttitlos iLl<ii¡;rtlr>s itll ii: íi¡¡ur:;.r l iiil(iil tlr)l'
pirirx.lo:; 2th y 3{)s (isl)t(lli1/,llIlililiP i';¡'¡rrl,,r ' r:;r;l+r; ilrl)l}pC 111¡-'J)tl¿s
tlt I,t pi,r'lida l(),ir(.,I r:rtl;i¡rlsti 'x¡r,'1lt' 'l-j: : "(:;'
illi(lEllil.l!rt li'1t{}: {17
{ )n¿ 1:raíí, ul:r deso-iire un rxrvintientr¡ ci'¡ctil¿rr urtiiorme según itüst¡a
l;r 1!i¡rla. I.l¿rl1.rr 1¿ velocidücl , rnrNli;¡ <¿nl¡¿ A y 11 si el ti¿mpo,
(oi.nlli¿n(lid{) elllrt: ¡iichr¡s ¡rrtnh-ls es dn 2s;
* ,i,*
n) ri(2¡ l).r'
l)) 4(2r l).r
.;;: !:ir,¡;:Á.1. #. L?jn t'-. :.9
:1,. ;,:.i¡-,*. ....!'
:i¿::;.i-fui,E{A$Hr
'4alr:í{ilr.}" ..,
t l 1{2n
E) 5(2n
Rpta: V, : jm/s
$tl{}lt[§lHÁ NIt0: {}2
tJn inrivil es c¿¡paz de recorrer uttiforntetrlenle 100 rnet¡os en 4
sei¡rrrrios, si el radio <i¿l st¡-. ilanlas es 0.2¡n. I)etennilre el v¿{or de su
vcloiidad au1¡ular tlurante el rnovinrienl.o t,
Rpta:W=l25rad/s
.,.t!r
'#Irvimi.nto
cireular uniforme, h
iij 1:;{.t,rJ.
[iP:]-ll!il¡i]l¿r nn.Éh::,üiia.r.
rueda
Pll{}llI,IllfA i§ll0¡ {}l}
C¡¡lcular l¡r rel¡:ción enlle l¿is velr¡ci<l¿rdes arr¡¡ulares de
sequnrie«r y minuter<l de un reloj olseg / tlmin
""
Pil{ll¡Lli,}L{ Nllfl: O4
más próxifii¡$,':i'if1:Pje de giro
i!li:.'o""
.:- ''i'|":l'i
':j"'
á,r
t¡BoBIB[il'lYB{h 0$
Con un iriiÉkumento de observación cuyo ángulo de üsién es 3", §e
observ-¿¡€l pa«¡ de un satélite artif-icial que se encuentra a ?6OI{m, de
ifil,nuf*i'§i el tiempo en cubrir dicho ángulo es l[s. Calarlar ta veloetdad
las aguiaS,.$l
,':..Rpta:60,,
ve loü:dáiÍ'li¡re al rie
*uyor .¡uá Ia velocidad
€n §u sup€rfiei€ €.t trc§ ueces
de los puntos qus se €nctreñtar¡ 5 cm
de la rueda. Determitre cl radio de la
Bpta;B=J.5cm.
lin ltr fi1¡ura s¿ tietre ti<¡s polctrs fijars t¡ue giran uníilas pirr.una correa
de transmisión. cuyos rixiios son li cm y 6 cm. Si la polea mayof'gira
a lfl0 r.p.m C¿rlcul¿.rr ei valor de [¡r fr¿cuenci¿r en revlmin. de [ir;4@i*i
frlenof
r:,: ,-::i{fp*a:'fs =E*6t!P,ln.
PItOBÍ.Ii,ltA NR(): (lí¡
lilr cielrtt¡ instanle la,posicii¡n del extremo dcif*e-quüdero de rrn rekrj es
¡ . t2.tli | |j,.. crn. C.rlcular el valor de srirvelocidad lineal en
cm/s.
PBOI¡LItHrt Nll0: 0(i '' r.: ''r I ,:
I-¿¡ rued¡¡ ttt¡str¿rda en la Iiqurl tle r¡rdi<¡s ll1"1m: R2"2rn, rola
uniformemenie ¿rlrtldo<ior de su e.ie. Si l;r rapiclez en P1 es 25 rnls.
Detennirre l;¡ vel«:ida<i angilla:r de l¿i rueda y la acelerrrión en rrt/s2
en el punto P2.
en Km/s.
12
'' npüo:v*3,.l(m/s
12
PBOBI,Eñ,I ¡t{Bü IO
Un reloj esta marcando las 9:00 hor¡rs. iA quá hora el horario y
minutero formaán un ángulo de 150'por primeravez?
RPtn:O9h IO'l¡1.6"
PtrOBI,BUA NBO: I I
En el diagrama indicado las poleas giran en sentido homri<¡ con una
mpidez angular de 2 rad/sr Si sus radios son q;: 2.5 cm. y rz: 7.5
cm. áEn cuanto tiempo la t¡arra estará en posición horizontal?
F** 0.8
---t
Rptart = 3s
PR0IlHIllANlt0: 12
iT{r Tienes el ltotenciol" No§otros la Experlencis,.!
'Rpta: V
5
--,n.cm / s
6
Rpta:a. = 1.25O m/s2](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-57-320.jpg)

![r(
ffian"***§,*
Rpt.:5r,[0 ru/.s
t,tl(lllll]]tlA Nll0: 2(i
Ll movimiento de un disco esta representado en e[ ¡¡ráfico. Calcular el
liempo que desacelerri y el ángulo t<rtal 5¡irado.
Rpta:O = 55O rad
PltOI¡¡,Il]IA Nt](]: 27
Los puntos periféricos de una rueda se <lespl:zan a razcin de 10':d5,
en tanto que los puntos ubicados a 2m <e Ia periferia sq desplazan a 6
m/s. I Iallar el radio de la rueda. ".r..
i'Rptá:R
= 5 rir
pnOBLIlMA Nn0: 2r
]I.'1;
tl,
i:n la figura la polea de ra<lio R gira con vel,,r'itlad."¡istáil$:,y
¿¡cciona a h'avés de una fai¿¡ a otras dos poleas solidarias .:, .¡ ,
l'lallar la rel¿rción de i¿¡s veiocidaries lineales.,rnlu
"r,rl
.n d..pl-uii
M y N respectivarnenle.
oo*,
,If- .-
E
vN B
l,Il0lll,lltrlil Nlt(l: 29
i;;;;;r"r. uniJu. untrn ií'tinnn,, radit.:s R, 3R y 4R respectivamente
tal c<.¡mo indic¡r [a figura. Si el bloque "4" baja a razón de 3m/s. áCon
que velocidad t¡aja "8" y con que velocidad baja "C"?
Rpta:V,, = 9 m/s ; llrc= 12 mls
GRUPO GALILEO
Pn0BLl]ilA Nll0: 3(]
En la figura se tienen dos poleas fijis que giran uni<las por una colrea
de transmisión. I-os radios de las poleas son de 12 y 4cm. Si la polea
más pequeña gira a 600 R.P.M. ¿A cuántas R.P.M. gira la de mayor
mdio?
Grd)
.S
RPtn:f2 = 2OO R'P'M
l,tl0lllJillA Ntt0: llt ,,.1;jjriiliilL' .
En la fig¡ura se tiene tres poleix tangentesi;H#ffi+ # menor radio es
impulsada por un motor que gira a 1800 R.P.[&]&üar la frecuencia
cle las otras dos poleas. iit "]i'.fi
Una partíoúf.ft1 $..g del reposo y acelera uniformemente de tal manera
que en el qütrl-iil.;#:g1¡n# realb'a 45 vueltas. iCuántas vueltas habrá
',t.ff3lirudo
en el tÉiá€lr::i. nndo de su movimienter?.
,i,,,,.
,. := Rpta:O = 25 ¡ev
Ptr$llBütlÁ NRO: il3
r. ñ#ii:; táb lu figur., tie¡e2} cm. de radio, parte del reposo y
cada sriffiáó que kanscurre su velocidad aumenta en 3II rad/s. [a
rueda ha*=mite su movimiento a la rueda B de 5 cm. de radio. Hallar
¡la relqeün de aceleraciones angulares y y e[ tiempo necesario para
i,i, rueda "8" alcance una rapidez de 1800 R.P.M.
(9OO RPM y 450 RPM)
RPta:t = 5 s.
PnOBLllüA Nlt0: ll4
Un ciclista que parte del reposo se desplaza en una pista circular con
aceleración tangencial constante, si al dar la segunda vuelta emplea
dos minutos. ZQué tiempo empleó en dar la primera vuelta?
Rpta:¿ :r(J|+ l)min.
PB{IRLIIIA NIIO: Í]5
Una partícula se mueve en una circunferencia de 20 cm. de radio cón
una aceleración tangencial constante de 5 cm/s2. dQué tiempo debe
transcurrir desde el reposo, para que su aceleración normal sea el
doble de su aceleración tangencial?
RPta: t :212s
PnOBLliMil Nlt(l: !|G
l¿ aceleración angular de una rueda'es de Z¡adls2. A[ cabo de 0.5
seg¡undos de iniciado e[ movimiento la aceleración lineal es de
13.6mls2. Calcular el radio de la rueda.
Rpta:R = 6.09 m.
PROIILIIIA ñR0: l]7
Determine la aceleración angular de una rueda, si se sabe que a[ cabo
de 2s. de iniciado el movimiento unilotme ac€lerado, la aceleración
total o lineal de un punto periférico de la rueda forma un ángulo de
60" con la velocidad lineal del mismo.
Bptarei = 0,43 rad/sz
il
.;
!* I ¡Tú Tienes el Potencia|Nosotros la Experiencio...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-59-320.jpg)
![rI§ICA I
PltO¡ll,BIIA NB(l: illl
Una parlícula se mueve por una circu¡lferencia de 10 cm. de radio
con aceleraci<in tangencial constant<¿. Calcular Ia ¿¡celeración normal'
de la partícula al cabo de 20 s. de iniciado su movimiento, sabiendt>
que al término de la quinta vuelta su velocidad es cle 10 cm/s.
RPta: a¡ = 1.013 cm/s2
PM)llltrllA Nlt(l: ll$
Una partícula en M.C.U.V. se encuentra girando con r¡ .-. I rad/s.
cuando t '=
.l
s. y su desplazamiento ;rngular es de 12 rad r:uando
t =. 4s. Calcular la velocidad brrgular cuando t ,. 4s.
RPta:o¡=7¡aüs'
Plt0Blllltul ñtl0: 40
Una partícula gira en una circunferencia de 3ni cle rliáinietro. Si en
t'.,0 su rapidez es de 9 m/s, determine e[ ángulo que <lescribe la
partícula al cabo de 6s, si en ese insl¿¡nte alcanzó una rapidez de 11
m/s acelerando unifomremente.
Rpta:0=4Orad
Filt§[§i{A Ntl}: 4l ..'"'
Una partícula que parte del reposo realiza M,C.U.V. 5i cuandot,.*. ]s
l¡a recor¡ido una longitud igual al radio de Ia trayectoria.-_Cafáular eL:,
valor de la velocidad an¡¡ular en rad/s un segundo deq¡uéÉ. l
BPta:r,l¡=4raÜs.
ItllOBLtiIlA ñB(): ,12 ',': ,:"' ., -: . "=
Un móvil parte del reposo y glira corr aceleración angular comtante de
4 rad.¿d. Si en k.¡s l" primeros segundos gira un ángulo "0" y
seguncios mas tarde gira un ángulo Q, tales que 0/O
. :,,',,r;filta:tr25o r :
Plt()B|.[ilÁ NIIO: 4ll
[Jna partícula con MGlJü--re.cortn iu pri**ro vuelta en 3S v tas.iüu¡üa
vuelta la hace sólo en un 1s. Calcular el valor de la vr ' ¿i6t¿d angular
.i, Rt,i;r,«¡i
Lil raa¡s.
:"..
PR(»ILEilA NIl0: 44 : .;.
Un cuerpo parle del reposo y describe un MCtiV cuya acdferación es
3 rad,/s2. I-uego de un dprerminado tiempo empi"-za a desacelerar a
nzón de 6 rad/s2 hasla (lue se deliene. Si el tiempo total que dernora
durante su movimiento es 30 s. calcular quá ángulo J¡ira desde que
parte hasla que : detiene. .
r. . ',..Rpta:O *ry rad
pf,oBlllM.f, ltü&): 45 .,". .jtttl"
La centrífuga de secado de una máquina léiv,adora esta dan<lo vueltas
a razón de 900 rpm y desacelera uniformemente hasta 300 rpm luego
de eJecfuar 50 revoluciones. Calcular: , .,,i'
a. l-a aceleración angular. '- ,,.':1 .t:
Rpta:« 1.;tr,tad/sl
'il,rl :' '
b. El tiempo requerido para efectuar estas 50 revolucioífoU
," . "
c. ,'/
Rpta:t = 5 s
trül§tÍllllA NRO: 4$
En un determinado instante un auto tiene una velocidad de 36 km/h
y luego de 10s su velocidad es de 72- km/h. si e[ radio de cada rueda
es de 25cm. áQué ángulo en radianes giraron las nredas en este
tiempo?
Rpta:0 = 6OO rad.
P*ODltiltñtr& 47
Una partlcula inicialmente en reposo, s¿ rnu.eve sobre una
ci{üuoferencia de mdio igual a 2ni con acelerac.ién tangencial
c$§*ailtis. eahdar el despla¿amiento angular c ¡anr;lo el cociente
s*s lbÉ médulos de la acelemción tangencial y normal es 4.
Rpta:O = 0.125 rad
A,CADEM GALTL§O
l,ltOBLtr[IA Nll0: 4fl
Una partícular descrit¡e un lnovirnignto circular uniformemente
acelerado de 1 ¡n. de r¿xlio si en el ins.tante en que el vector
aceleración toial hace un ánE¡ulo de 53" con el vector velocidad su
rzrpidez es de 2 m/s, determine el rnódulo del vector aceleración
tangerrcial an ese instantp.
flpta:a = 3 rrls2
Plll)Ill,Hitlrt ñIt{): 4!)
L.n el instante mostra<lo en 1¿r fiqura, una padícula que se mueve con
MCIJV, fiene una rapidez de lJO mrs y aceleración Í1 <¡ue hace 37'
con la tangente a la trayectoriar cir"r;ular rie lim de rarlfu. f;ul.ufu.
lll
Rpta:a=30Om/sr
l'llOBLljlIA ñltll: 5{l
(Jna partícula realiza un movimie¡rto circul¿¡r con o. .-, 10 rad/s. Si a
los dos segundos alcanza o¡,- 20 racfs en otro instarile la cotan.t¡ente
del.ángulo.q¡1q,formán lá velocid¿¡d c<xr la aceleracirin es 9/5. ¡:alcular
el valor.de:tl'i,rcrJ.éste ríltirno inst¿rnte.
P.AI}üLUIIA NnOf !5l;1i
tl-i¡á:l¡.;:p¡rtículai'gr,rrrfiO{-Jv tiene una ¿¡t:eleración normal de 5 m/s2
cuáadti,se d¿§pl¿ü.ú:r':f, rad. y la aceleración norm¿{ es <le 9 ml*
c+r-an<*O,e-!desplaz-ár iñk> an§ular es de 3'r¿¡d. Calcular la aceleración
láñgencial de la partícula.
Rpra, r..=.1-
v5
't, .:
,,:::,j:.r1j-=r; r..1
PROBILI|A NIl0: i-¡2
Uná partícula realiza un MCUV
instanie su aceleración cenlrípela
,
-Rpta:a=1nr1s2
,"i
"partiendo §E[..ieposo. áF-n qué
será el dobiü'de io que er¡¡ en el
Hpta:t = lJl ,
PIIORLüIIA ir§R(} i¡3
Una partícu,lárque partetel reposo describe un ntovimienlo circular
con un milio de:40,cm Si en un instan*:1i0. el áneulo que <lescribe
es 27" y su.acelemción es a =- -501 m/S'. l)eternirre la
vdlocidad en dicho instante
PNOBX.tsilIA NB(h 54
Rpta:v = 4 m/s
Una partícula realiz-a un movimiento circular partiendo de reposo y
coit'aceleración angular ü. ., 2 radls2. Si lüeEo de 1s. su
áieleración es 1fi m/s2, hallar su acele¡ación nomral transcurridos
2s. de iniciado el movimíento.
RPla:a¡=8m/sz
PB0BLf,llANB0: 55
Una esfera de 4m de radio empieza a girar en t , 0 s. con
aceleración angular constante <le 2 mdls2. Si después de cierto tiempo
t(en s) la aceleración cenkípeta del punto "P" es igual a 50 veces su
aceleración tangencial. Detennine el instante "1".
ülffiura**n.Ío áv. Oa Ir firü.rrs fiX6 {ftw&.a b aNSAAC)
Rpta:teEs](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-60-320.jpg)
![r
¿{cadsu¡la Ci
/*. *aa
PIUIBLüIUA Nlt0: 56
del siguienle .t¡rá;r.{ir:o. tlctermine
1l s.
GRUT'O GAI*ILEO
A partir
Para t :'
la posición dr: la pafíctrla
i -,r-lJ": --/' itt
--+:: *-7¿-:-*-*---.."."+
i/21
RPta:x = 296 m
l¡R(lllllillil ñlt0: liI
[Jn proyectil es lanzado perpendicularmeqtg.,...A.pn plano inclinado en
28". Delermine la velocidad final con, $$ano inclinado, si
77 ^','",;"'+&
demora un tiempo de t , . -;§ "S '= tO m/f -''It
5I'.
a) 3m
d) 4m
b) 5m
e) 10m
c)12m
Plt(lllHlüÁ Nll{l: ir7
Desde los puntos A y B se lanzan en e[ mismo instanl.e dos proyectiles
en un rnismo plano en la forrna indicada.
l)etermine el tiempo transcunitlo hasta que choquen.
g ,. 10 m/s2
''BÉá:t '= ¿ s
pl¡oB[rtr,rr NBt]: ¡i8 =,li§"ll.?fi.
I iallar el valor del alcance horizontal sotrre el plano inclinado. '':'i{*..?¡i;
rll&lllll,B,IA Nll0: .62
Óáicrrlar- el valgr'ldel alcance horizontal
noriráñffiálitá con una velocki¿iri v '=
distanciaiF15 m.
Rpta:Vr .,JSl
^¡,
X, si el cuerpo es larvado
aG n',lu y describe una
u
A"
1§
s .. i,!=trYs'z
.,,,,,,
PIIOIILEMA NR(l: Gl)
Determine e[ valor del alcance horizontal del proyectil que es lanzado
con una velocidad de 50 m/s bajo una inclinación de 37', tal como se
muestra en la figura.
g .- 10 m/f
Rpta: x .= 12m
PEOBLüIIA Ntl0: G3
iCon qué velocidad en el momento de lanzamiento de un cohete es
necesario disparar de un cañón para destruir el cotrete que se lanza
perpendicularmente con aceleración "a"?. La distancia entre el cañón
y el lugar de lanzamiento de[ cohete es L, el cañón dispara bajo el
ángulo de 45'respecto al horizonte.
Rpta:vo ==Jtt,;Sj
PA0RL*üANR(I:84
La trayectoria de un móvil es la semicircunferencia de radio R '-' 4m.
PBOI|L|I,IIA NIIO: (iir
Calcular la velocidad i'nedia en m/s entre A y B, sabiendo que tA ': 2 s
9ts'-'4s'
ai-0.27 i
d)i + 0.27 j
¡Tú Ttenes el Poteneial. Nosoffos la Éxperlencia...Í
i:'r ptarl- ,..6,6'l m
,$l¡(tBlaila Nl¡0:iÍp .il
Calcular el vabr d!i.il[á: elocidad inicial para §iie el proyectil impacte
en e[ punto B. .]
g ,, 10 m/s2
B
}sJiRpta: V, =-m / S
b)zi + O.54i c) i- 0.54 j
e) O 27i 't' J
A
r * .. -' .|' a00Tm](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-61-320.jpg)

![ffire@§
PIIOBLIIMA Nlll)r 75
Dos proyectiles A y B son disparados con la nrisma velocidd inicial
V¡ pero con ángulos de inclinación diferentes 0¡ y 0s §i 0¡ = !0o, la
relación entre las magnitudes de las velocklades de los proyectiles en
el punto P de cort¿ es:
a) Vo ,= 2Yt
b)Vo=Yn
c) 2V^,=Y"
d)Vo=Y"6ot16o-t",
e) N.A.
PnoBl,nilaNn{h ?§
Dos proyectiles tie.nen el mimtc slcanfe horirorttal R. El primero (I) s
clisparado ho¡iesdakpnte dp*de una aitura h. Et segur¡Co (H) §É
encuentra dirsctalrenb debdo del primero, cr¡an& son dispardm
simultáneamente tal eorno, §€ muestra en la figura.
En que relacién se ericalofikan kis lkrnpoo d§ lddo d€
prq¡ecüler (t¡/t¡).
GR¡,'PO GALIÍ"§O
PR(»¡illlIA Ntt(): ll{} :
Para el tirc¡ de un proyectil (ver.fig.) s€ ensayan diferentes velocidades
iniciales con el obieto de otrtener el máximo alcance AE. La velocidad
deseada es:
v
d(90'
a)3i+2j
d) 4i
tt)3i $ 3¡
el 6i
PROrrLnüilffi 8l
En que prqorción
horizontal. un pq¡cc§l si se
d 1m'
d) 40
cemd#
215
a) arc tg 2
e) 30'
fnaxrmo
eñ !.0%.
all
2
d)2
m. de dtrrra; se disp&a con un
ffi grenada. l"¿ wlocidad iniüial de la
dA qurí di*tancia de la base del acantilado
(en mehos)?
c) 319 l
a debe se: lamado un proyoctil para qt¡e su altura
igrrd a zu ¿rleanc¿ hori¿onbl?
d) arc tS 1/4 b) arc tg 4
c) 45"
bl3.o
e) Ninsuna
d€
lade
a)o
d) V62l(g sen o) e) N.A.
IrR0lll,lillil flt(|: 7ll
[-a velocida<.l <1e un pmyeclil en el punto nlás aito de su @rffi e
de 10 mls. Si ade¡ds su alea*re-e egde l0O m, la vdsci&d ffi #
Sq¡ectil es (en rnlo): conci&rar g = 10 m/S:
PffiBX'H{i[ilEO] fl4'
De* b F#ffi A y B se lan¿an en el mi¡rno inshntc dos proyeetiles
en uE rriho¡fuloffilia fo:ftn§ i*dl€ada.
§ffinmffi
De&nn'inar el ücmpo tranrcunido hasta que choquen: (en segundos)
d)416
b)2 "t}Ji
e) No ctrocan
:::a:4
!'ill:
;i .:.1
t" ""
a) 4
v
I
jffi
Pnorlfllill0¡ ?? q
Una bola d¡ biü¡i !üh rodando por 6ü boúdr 4¡man¡m
de 1.2$ m d¿ altr¡¡a, $¡ cr ¡l rr¡& m uft Ps*CI fudo a
horizonhtncnte más aáá &l bffde r*e br¡m, ledreldd {en
al salir dc h mrsa era: (comid¡mr g=1ü ñIft
a 2.5
d)4.0
PBOBIJITAÑtr& 7B
En detenninado lnñtante to
indica en el dibuio,
&l úüarru to.s:
b) I .lJl
JT
ell
c)35
a) l0+1ü b¡ loi+& cl10i+5ü d) 1CIl+6q *lN.A.
iTtú Ii*no¡ el Paten clal, Nosaúos la §xryriencÍa',J](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-63-320.jpg)


![,
FISICA I
:il*#+{:
ACAD§MIA GALIL§O
?
;7,1
ll,,:i I
tlL*i
ventano 2
JL
ni-l
tÉ] I
I v*:2r,
J
venton0 I
Plt(llllBilltNR0: I(lB
Sc acelera un disco rle 5 crn. de radio, que se e,ncuentra inicialmente
en reposo, alreded<¡r cle un eje que pasa por su centro, con una
aceleración angularr de 3 raclls2, después de 2 seg. su aceleración
central es: (en crn/s2)
b)39/4
e| 3sl?,
c) 2-t¡ .1-...,'-
a) 180
d) 150
a) 1.60
d)2.05
b) 16 c) 3O
e) 900
l
c)1r;v
Pn{}Bl,liHA Nlt0: l{}Íl
iln uaa xnimera a¡rroxirnaci<itr se puede consider¿¡r que el elecirón del
átr¡mo eie hidrér¡r:no s€ mueve siguiendo una í:rbiÍa clrcu.lar eon una
velmidarl eonslante de 2 x 106 m/se11. Si e-[ r.x].io de la é¡br:ta es de 0.5
x.
.l
0 r" rn. ¿Cuánto valdrá .ia ¿rce.,le.r¡¡ción c{el ¿lecl.rón?: (en.mlsef)
a) 8 x l()2
b) 4x1,$' ,
c) 10 x 102
d) l0 x l0r'
ui I".l{t" : :.i. n.
"''
-i
Pttlrltl,¡liuil Nll0: l()4 ,i,,.,. .j', ,l .
Si un cuerpo se mrreve sobre u$¿r circuñfiure¡.éiq,qon unit v3¡oaidad
c<¡nstante el rn;rgnilu<l^ iguail a lzr qr.re.ad¡¿uiáre eaye-n<to-#Bi.e4erlte
rlesde una allur¿r iquai ¿r Ia rnit¿¡d de.i ¡ad:io de la eirurnfd-iesda, éer¡áI
es su aceteraei<in er:nfrípetir?
Ptt0BUlltÁ NtrO: l{}9
{..}n ccrche A está detenido frentc a un semáfr}r,r.¡. Se encieurde [q,ha
verde y A arranca, en el mismo instar. te en qu€ un ffi*le & üe
adelanta. I-as 1yáfieas (V" g de ambos cotfres.se.kdi§qn ce.h&1¡§6.
AI cabo de 0.010 h. l,qué coche está ad¿lantado y que dietalreia hay
entre eflos'/
a)2V
d)3v
d) tvz
d)s
a) w 12 r3Jr,
c) w qr3/r2
b)lrv
e)'l V
a) A adelan!¡1,g U en CI3 km
brA adq-lariité;ii8 e¡r,0.1 km
e) Il adptffita"á: en 0.4 J<m
i]
Un cuerpo rie masa M.giratñ'üna circun{e¡*neia de L;rdio R,'guo$é dq
masa 3E M gira cr¡n la misma velociil;rd ;ur!¡ular *n'' ot§
ciret¡nferencia concéntrica con [a anteriár rlcu radio .,ffi.'itB.. La
dlferencia de las magnitudes de sus aceler¿rciones centlp.ffi{{I.. ;, .
(:a con la anlerjor tl,r radio W."-B L
des de sus aceler¿rciones centlpi{ffiffiffi
) r- ..5
",--2n
'.¡''Jü:'-r-.i
a) 0 d) J w2 R ' b.)r,.i" Irt *'R
44
nLwzR .) lMulR
2 2 ,,'i"
PBIIBI.ü]{A ñlIO: IOS
Si el engranaje A gira con una v&óidad 'Alg¡.¡lat
radianes/seg., determinar la velocidad angular de¡E.:;{en
Plt0llU¡lIA l§lt0: lOli
r¡,,4kmehos
r¡ ...
0.5 K metros "'1,,r¡..o
rB :: 3 K mehos 1r'";"
al5W4 b) 8ll3 cl12K
b) 6K el4W3
pG$B!"BüANSlh r{r7
Un disco A qu€ gira con una velocidad w, hace girar otro disco B. Un
tambor D es solidario con B y gira con é[, levantando el cuerpo C. Si
lcx mdios son r¡ ;', t1, rs = rz, ÍD =' 13. Calcularla velocidad de C
'í.lLirxrrür¡no: lrr
El á.ffi¡5'r.corrido por un móvil (en km) cuyo gráfico {vt) es el dc h
6gutá,;¡{is:
,,,,. , V(trff )
a) 4d¡.rr,
{}
lo
B"o
e) N.A
-6,0
t 2.65
e 2.15
c) 2O
c) 0.80
b) w qr2lri
d) ulqralr3
PllOBLlIltAN[0: rl?
En un cierto instante, la aceleración de una partícula es a : -1Q
m/segz; si para t :', O s, V6 * 3i "t" 4j (m/s) y 16 = Om, entones sr¡
vector velocidad V (t) en función del tiempo será:
A)-4rj-Vo
B) -10tj + 15i - 20j
c)3i + (4 100 j
D) 3i.r (10t4)j
E)N.4.e) N.A
V(rryf'!
llbfconos en la Ap, De la Caltura70l6 (frente a la UN§AAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-66-320.jpg)
![a
Jib, t."clerni a (ial i leo*,§Á
-la .*-ia feaaa'e
PItORLHMrlNlt0: llll
La posición de una ¡:aftícirler que se l¡rueve en el e4e dc las X depende
deitiempo. tlt: acuerdo ,, ,,,
",-|u|:,i}, ,,
donde x está darla en metros y t en segundos. I-a ltxr¡¡itud total (en m)
de la t¡ayec-toria rr¿corrida clutante lcrs printeros cuatro segundos es:
EJERCICTO§ NIVEI- C.B"U.
1. Un ciclista que se tlesplaza stüte urra pista rectilínea pasa irente
aun:loste con una rapidez constaute rie 5 mis l-uego de 10 s k>
hace un automóvil con urli.l velocicl¿:d co¡lsi¿rnte de ,'20 rn/s y en la
misnra direccirin, cleternine lue.r¡o de cuárntt>s segundos cie hatrer
pasa<io el automír¡vil frente al poste" el ciclisia es aricanzado por el
autornóvil
a) 10/3 s
d) 10i7 s
f;. i:n r:i gráfico "espacio'l<zrnpo", se pidc haliar ei v¿¡lor de la
vr:locitl¿rd del móvil más r;iPklo.
X(m)
CR.UPO (;T{LTLEO
A) 1 crnis 13) 0,1i6 cnris C) 0,45 e
l)) l).(,1; crn/s 1.7 0.5 t nr.s
5. Dos ¿rutc»:rírviies ¡rasan sirnuhiirneaillente por lzrs estaciones A y B
como se muesira. Si cu¿indo se cruzan, un rnóvil habrá recor, klo
36 h¡ mÍ» que al rrirc. y a 1;adir <le ese inslante el prirrtero li:rdzl
t hora en llegar;r 13 y el -.e¡¡unclo 4 horars en llegar a A; <lel¿nnine
la distancia enlr€ ias estaciones si son rtnirl¿s por una pista
reclilínea. ((lonsiderr: quc kls aukxr*rítilee leaiizan M.R.[J. sotrre
vías paralel;.rsi.
Ai 106 Km. t]) i0fa Km
Dl 10Ii Kn' ,E) 102 Krn
B
.c).ior)..l&r
i)i..
*
[)os autrrnlóviles qu€ s€ t¿neuentran ou lo. .&t emos <1e ur¡
puente. se desplarzan el urio-,:el er,icuentft) d¡l ltrrs' Si <¿sk¡s
rnovimienlos están repnrsentatll;s-e,iá:el gráficq. calcular la iongitud
del larqo del puente y,l¡r v<Jociciadüblf{}éüil ñr᧠rápido
A)?"4
p) 20
B)22
tr-) N.A
A) 32 m/s 13) 30 rn/s
D) 26 m/s L:) 34 m/s
b) 113 s ci 5i3 s
e 312 s
(') ll,
Cl.li:2fi mls
A) 30 m y 3/4 m/s
'. Ci 30 nr y 114 m/s
E;} a:yáamls
I3) 20me3l4mb
I)) 20 m v ll4 mls
6.
3.
C) 28 mis
rr l':,
_,::-_
(Jna rnosquila recorre las ,)ia¡;,r'abs 7l ;l'--'
t;.]"ffi.,
,,rr
cubo con vekrr:id¿rdes consla¡ttes respeclivarl , ¡te. que stin:
::
7. (-ln #iáta recorre el perinetro de un parque que tiene forma
re"qtángular, tal comc¡ se muestr¿¡ en el gráficolos números 2,3. 4. Si su velockiad promedro es ll mls. Halla-$
rirpidez media (promedio). "r¡j;
l)
tA
4.
Si éste parte del punto A. empleando un tiempo de 40 segundos
en el tramo AB, 25 segundos en el tr¿¡mo BC, 35 segundos en el
tramo CD y 4O segundos en el tramo DA i,Cuál será su velocidad
media con que ha recorri<io desde el punb lJ hasta el punlo D'?
ttl 2:7'l mls ''r¡s,se */.
D) 2,14 mis E) $,18 m/s
,..; jtiii : I ::::,:,,...
Se vierte agua a urfiá" -dali&ise cuadrad¿i de i30cm de [ado.
F-l nivel dei 4gt¡a gtrbe éon üñá rapidez de 0'3 crn/s, de tal manera
q.u¿ el .ls€lpieít¿ se llefia ,en 1,5 .m'inutos. Si una horr'niga inicia su
escape dásdé ¿]fbndo qqanaando sotre la varil{a AI3..ácuá} será la
velocidad mínirna ccmstante, aproximadamente, con qtle deberá
avanzar para ño ser alcanzada por el agüa?.
a) 513 m/s b) 5 mls c) 3 m/s
d) 5/2 mrt e) U3 m/s
Un autornóvil recone 1{) Km En línca recla hacia él liste.
empleando 0,2 horas; luego reg¡resa 6 Krn. L-n 0.3 horas- I lallar la
velocid¡xl media..
A) 8Km/h Bi 4 Kmlli
D) 1O Km,fr E) rr l*nfh
C) 2 Kn/h
9. Se muestmn 4oe vehfcrllos A y B sobre una plsta rectilínea, A
realiza un M.R.(l: con Ena rapidez de 8 m/s, mientras que B inicia
un M.8.U.V ccy-.& Igla aeeleraeión d¿ mddulo a "" 3 m/s2, ¿Cuánto
detre set 1a dk**ncia d para qu€ [os vehlculos se cr-ucen una sola
vez?
E.
a
--**
f .i r.l
120 nr
.- , ,, i ;
[=66:l ¡ffi ffic-ü€sÉ¡ Plo.rewisl. ¡i:asaln:osla Expertencia.,.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-67-320.jpg)
![t"--
i
§§sg§e-§*-. -
IS.tlna parlícula s¡l ñrucv{¿ sobre el {ijc X c¿)nlt)j.!n(lo su }:ostciórl rn
lu»cki¡r d¿l tir:n'rpo se.qriri la liltiiictr qr"te se mues{t:r. C¿rlcular su
rcr:r¡rririo enfre t, 0.5 s y t. 'l¡,'l s. (tarn rr .,4)
tangenle
cI0,,55,É
12. U¡ra parcona q' s¡¡¿p6lt'¡tlir der¡1.r<r de ttn dseensor quer§e €t{lva c{}n
ar:el¿ración constante. A l.S,m del pi¡o *l&i ixce.lr¡;or Ia Berst¡th
', aueita {¡m moneda y esia inqiacta eE q}pise hizgo de 0,5.s.,r"
áQué acrllet'aci(¡n experimenta elasqen$or,9 {¡¡ * 1,0 r,¡rl¡.j}: r,,
ai 6rnl*
dli xlh¿
1$. I-a -qráliea ,f
mtxiles A y tt,
inslirnfc en que
segun<la vez.
C) 8s.
1.0, [J¡¡ r-¡rivil qrl{r }-c.-i)nc (lrra lrallecif)iiil «:rla.rie..105 tncirt»' inicicr
su movir1)ier)l() (tr)n u¡ir vel,tciriarl illilril dr¿ 2() ¡nls y aceie¡a a
,-On ¿0, 1{) rrlir-.z. (-'¿rlclllar el lienlt¡o errrple;lrl5 y srr vebci<l;rd
Al 20 ¡n
l)) l() nt
i ir:.r1.
a) li0 rl/s i)l l(l irr
d) 1.1; rni:; i') )1r:l
ar) 6 m/s tr) il rnls
cl) I nrls o) 5 nr/s
ll) ill) rn C) ''r m
i:.) ili rll.
11. [Jn ¿rLrtonl(;vtl t;iti;ul¿r ]l{)' llnir 'rvct"titla
r€cli'} !' st} ha r¡tr"-r:t'¡;ir}-'
que lo posilit'nr x Eici vr¿hiculo c-rl¿i darli:' rQt br 9.9*ioÉ", x(t) iil
i 12 i",rrt t r.:rr se.t¡ttxios y I ':ri r¡¡*rrs}. lí,rryrin¿ I¿¡ v<rlocir:l¡id
rnedi¡r cn rn/s tlel ¿litttrm<ivii el'r)l .ir.rfervaio de iietnpoi , 0 hasia
t 10 *eguntkrs'
i ',i t It s
c) 2 rlls
A) 6,58 r'a
D) 0.5¡9 m
B) 0,56 n
Ei 0,5 mL¡) I rnls? c} ?" rnld j
e) 5 nVd - ' L r'i lt1, .¡'' .,
.'
: ' t ...''_
:
1 n{xi ffiuestra el ¿s¡ir¡e áe. Posiciéglds {iqsl
co¡rlorg¡e trrnsqui'rá' d,tPr¡rpp; S$.{-li¡{oin€, el
los rnóvifu¿s se encug.Iqlan sgpa¡'¿iü$'¡E r§. por
16. (Jna rnoneda se suell.¿¡ desde cierta altura respecto a la superficie
pges.@¡",§i otrservamos que en el último segundo de su caid¡
recoxueww. adesrle qué ahura fue soltada la mopeda? (g '= fO
S. ,, '':''tti'.,'rt .r'ri.i..
a,iili60* ,:i i'; 8Q¡rl
r,$I.s0m ,.r-,..i,.,. 40m
. --.1_ i , .
ri';6Éiae onaii 'a*
100m se deiit4aer una piedra v al mismo
t¡erirpo desde la strperficie rle la liera es tanzada otra piedra. Si las
aos pi¿dm§. tii.npn la misrna rapidez cuatrüo..se c¡uzan, áa qué
disianciádeja superficic, tas dospiedr:rs''§e cruád k = 10 mlsz)
A) 15m/s
D) 5 m/s
;1ii1li
'il;
B) 25 rn/s
C) 12 m/s
c) 70m
' ..j,::
c) 60m.;;.","
',,: ,,.,
i,iáf-os 1¡t<üc» aer<isfáticc¡s ascienden uérticalmente c«¡n velocidad
::..J constarite. Si en el instantq.*nostiado desde el globo A se Euelta
una monédal'y luego de'.6's la persona ubicada en el globo B
ahapa lg.:'rtii*reda, dá-teímine la rapidez con la que §e encu€nta
elevando ¿t:qtot o A. {s = l0 m/sz)
: : .. j :,rit:li"i"!,;!.1:"
a) 80m b) 75m
d).$5m c) 65rn
A) 12s
D) 5s.
Il) 10 s.
Il) 6 s.
14. l.a grafica nos mucstr¿r el comportamitin'to de'fa posición de un
móül, q.ru se desplaa en línea recta con á'eleración consti'nte''
f)etermine la ¡rcsición g rapidez- del móvil para e[ insta¡ite I -' l§jt
"
A) x,. ,10m y v,' lZmls
I3i x, ,6m y u, ,6*lt
C) x, 5m y v. Zmls
D) x,,8m y v,,,10nVs
li) x,6myv,.,llim/s
ubícanos en la Av, De la Culturu70l6 {frente o Ia ÜNSMC)
450
lli¡i,i
iII
C) 10 rn/s](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-68-320.jpg)
![,".d
i#;,
¡r: irclt:¡:: ia { i¿d.ilct :
",*",tu t23.-4::z*
19. Ia figur;r ¡nües{í¿! li.r Elrofica vclociC¿id versus iiet-nptl tie un
r,ehlculo qLtáse mucve En l'fnc¿r recta. Ouál szré ia distancia que
¡ecorre. en molrr§. enfre krs insfantes f ,,,' 2s y t " 6s?
§RI.}Pü §A¡-ILÉO
25.5e lanz¿:r un pnryectii con und vel<¡ci<lad inicial v" - ZOO t6 nys,
como 5€ mucsf¡a en la {igrua. }'lallar (I .
A) 9{)rn
J)) 86¡n
ij) 96nr
C) 9,8m
(s)
(i) 80ir:
: r;- :I :r:r::r::::::tj.
i¡jat¡:i _=._
)o ^ ;l :,i),'.
-/
s :
-C) 60m
A) lí1"
ir) 37"
c) 45
D)26.5'
r:) 60"
26.lin el gráfico se mueska el
375 rn
Hallar el
tiempo que crnplea
' ,¡-
2ü. iJl'r ¿rvii;1, es1á etr 1;ii;;ida y irltrnirncicl un árngukt de depizsión de
3'l". (-Lrando st¿ en¿:uentra a 425 n de altura, se c¿le un neum¿itico
ller¡a al s..rck; despLres ds lj s. áQué rapklez tenía el avión en aquel
ins.ia:r1c'¡g 10rrt¡,.:')
A) l0on''
B) l0l, rnls
(l) 102 ¡n/s
l)) 120 tVs
C) 110 m/s
21.Un objeto es latrzado oblicuar¡rente con uri¿r rapitiez de 100 */;;
dete¡mine el lieirtpo que tianscurre desde el inslante que- gs
lanzaclc¡ h¡rst¿r el instanta qur: adquiete una velocid¿irl de m(fl¡tlo
20 ,ii *1., el r:u¿rl ürmr¿r Ltrt anguLo de 9tJ" con ta ',elocidáá'!e
l¿inz¿rrniento.
(g';' 10 r¡kz) ':
A) 129 s B) 29 s
r)) -,128 s I:) ,,30 s
A) '/5in lfl,,EQn:
i-I65m .C):55§r
vak¡r de la nrínima velceÉad
antes de tocar el a§ith.
ti'
-... .r' ')<. /-r i^ l.
C) -
-,¡J m/s; (VO +
2
D) 25 m1s; 4 s
r) srEó,n/u; rEO u
;i:
i
ji22. i)e una ahtrra'de 8O rneiros,st, t.iel¿ c¿.l€r u.i:-qtie!Q :!8 segundos
después y.'de la misrna alura. se ial¡zí vql*icalrrienle con una
velocicl¿¡«j. ;r otr,o objetcr.,ccuál st¡rí:'l¿r veklói<l;i<] inicialt üé'. dehg,l
'' lefi¿r este- últkno otrieiri l:¿r¿. .jl.lr' (11('¿ince ¿| 1:riinr:rtr,]usdd,p.$áridé"
llegrre al sueb? :
A) i0 m/s f3) 20 nrls ( I l¡ír nrrs
l)) 5 rrris L:) 8 rr,'
2li. I)r:sde una alluraile L(r', ¡ir sc dejp.:caeiluna ¡:ar1ícula y a[ mismo
tienrpo desde.tii*,r r* proyec4üa olr¡ '¡¡,I'ctrl¿r vedicalmente
ha,.:izr ar¡itrr:. ,§i las dos parlículas rir'n( ] ,1 misln¿r velocidad
cri.)n(lo se encugniran. <,Qué aliur.l il¿, rccc¡rrido la partícula
i, rtrz,nl,r de:rtl,' lierra.)
27.1-a eslertta metálica que se encuentra en el punto '4", empieza a
r-odarse por e[ plano inclinado liso A-8, hasta llegar al punto "C".
: Hallar el valor de la altura FI. I
eltEm
24. [Jna mana]ue.,a con trótit*tltrd déscarga uh ch<¡rro {ie ;r1¡ua. cuyo
v¿rlor de la velócklad inicial g.s ri¿ ,1 .10 rnis. l'lallar el aicanee
.rnáxifio "1". 6i se sabe que'la'altlrii rnáxima del chorro rle agua
eslul
.ry,re.¡p
rJ
#):.+'i"qrn
§Le"S
$rt q.
28.Ur.r nqdarlo"qus típr.ra una v€'toeidad de 3 rnls en aguas
&anquila¡, deci4s oRW ur¡ üió ds 18fu¡ de eneho, cuya e§nieñte
*te suo a..g¡¡al tiena w¿a vdsgidad de 4 m,&; pará tal efecto se lanza
tresrldLsqtqs*l*EB a la oailla dd río. eakutar el e§pa€io
req$.&.$ak¡'itlp,f "d *a&drr dula{-}Je srr tre'{¡esh.
A) 10m
D) 10,6¡n
4iffi.0-m
D)200n
B) 11 ;4 rn
Ei B,B rn
t]}?50 ¡¡r C) ?95n'r
,§) 1$m
t:.
C) 4VJn:
L.{! 4'i rI g
I e I P at'"
€ !,{: iq l. $ps¡r¿ Í¡ os I a Í} xner i o n c i a... !](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-69-320.jpg)

![a
Amd.emx{m'ü
-8a ¿*á¿
38. Una padfcula se mueve <¿n una circunferencia de mdic¡ 50 cm de
'
acuerdo á {a siguienté relación e,..1,5t2-5t- jCuá[ es el valor de la
ac'eleración tangencial y su lecc¡rrido en t " 4 s?
A) 1,5 m/s2. 1m
tl) I m/s2.2m
C) 1.3 m/s2, lm
D) i.5 m/s2. Zrn
E) I mls2. hn
39. Se mueslra una pequena esfera que está adhericia a un aro
metáico R : 1 m. Si en cierto instante Ia esfeiá presenta una
acelerircióh de 2O mlsz' y fonna un ángulo cle 53" con su
vebcidad, i,qué rapidez.presentará la esf¿ra en dicho instante'?
Un automóvil, vjolando las reglas de tránsito, se mu€ve a 72"1*r"rt¡'t
en una zona dánde la máxima velociclad es de 40 km/h."Un
policía motociclista arranca, en su persecución, del r€poso con
aceleración constante de 0,5 m/s2, justo cuando el auto pasa
enftente de rli, iQué tlistancia recorre el policía hasta alcanzar al
¿ruto?
A) 1 knr
l-r)1.6km
B)1,5km C)1,4km
E)1,8km
Un ratón se dirige a su aguiero en. línea r€cta con velocidad
constante <e 2 mls; cuando le faltabra 5 m para ilegar, pasa por el
lado de un gato, que se encuentra'en r€poso. Si el gato acelera a
razón de 2 mls2 en dirección del ratón, iel gato alcanza al ratón?,
ia qué rlislancia de su agujero?
A) 1 m tl) 0,8 rl
Di 0,5 m E) N<¡
7. Un auto que tiene MRTJV salt del reposo de3
con velocidad
sentido.'¿Qué
2
C)34 m
D24m 1ir'::{':$}14m
E) 3 mis2 Ei 3,5 mlf
B) 1,2 km C) 1,5 km
E)2km
A) 1s
D) 4s
mfs2, en el mismo instantefjln camién lo
constante de' 9 m/s, en ld.'..'fi*is¡na direcci
distancia recorrió el auto hast#-ffie¡ al-ca
lllf* 9l#* ''."L,,',1'
##,f¡.T
A) 3 rn/s
D) 5 m/s
B) 2 m/s
F.) 6 mls
C) 4m/s
40.LJna.pat'tíctda irricia su ñouimieeto px una circunferenc!ffiS¿
radio- 50 c{n cor} l¡sa acebracién tangencie* de n: dulo con$?ile
e iE¡¡al a2,5 lt ml*. Deteflairr€ s* r4ridm tangencial y angular al
firralizar la guinta vrr*lta. .::a
A) 5 7I m/s bl? tl *ls c) 4 .6 rrds
D) 6 /I m/s e) 3 7t rnls
9. Un aütiir¡r6vilque tiene MR1JV sar'ra su r¡ehcidad de 18 knih a
72uÍillhá".irl.jeg+ná"t. áCuál es la accleracién del autornóvil?
tr , A) i,5 m/s2
''' .',:,,,1 Bl2 mlsz C) 2.5 m/s'z
PROBLEMAS DE CINEMATICA: 2OO9
l. Un rnóvil con MRUV tiene la siguienie ley del mo-vimiento en e[
eje X:
4|f'k"
P)1,Slsn
11. Un leopardo puede lograr una aceleración de 8 m/s2. §iva a la
caza de una gacela que puede lograr una aceleración de 4 mls2, y
si ésta inicia la huida desde el reposo en el mismo instante en.que
el leopardo está en reposo a 18 m de etla; ácuánto tardáiá ei
leopardo en alcanzar a:fá gácela?
B)2s C) 3s
E) 5s
12. Un zorro puede lograr desde e[ reposo una aceleración de 3 m/s2.
Si va a la caza de un conejo que puede lograr una aceleración de
1 m/s2 y si éste inicia la huida desde el reposo a 36 rn de é1, iqué
distancia recorre el zoffo habta a[canzar al conejo?
A)54m B)44m C)64m
D)74m E) 18m
13. A un auto que viaja con velocidad de 36 km/h se le aplica los
frenos y se detiene después de recorrer 50 m. Si tiene MRUV,
cqué üempo demoro en detenerse?
A) 5s B) 10s C) 15s
0)20s E)25s
14. Un automóvil que tiene MRUV, sale con velocidad de 4 rn/s y
aceleración de 3 m/*. Calcular la distancia que recorre en el
octavo segundo de su movimiento.
e.l lr".
x(t) 8l-31'z ::"
Donde t rep.esenta al tiemp (en segunffi), X l+ipo§éjÉ-b#fi
mehos). l,En qué posiciómrsii- acuenha enfi§.fii¡starif.b t = §'s?
,O 'n'U]-.t**6vi1 "que tiene.MRUV inicia su'móúimiento con
""ióái&d
de 2O m/s. Acelera ¿r razón de 2 mls2 hasta cuadruplicar
su velocidaci. entonces iqué dislaincia ha recorrido el auto?
Blx ' -3lim
.,"! D) x .. 35 m .r: : .,1
3.+ri:_::..!1.
.::.:j. j ;:iirjiiiiiiü,,
.4, -
2. Un cuerpo er'ird,itiene MRUV, sale del reposo en el punto "4"
¿Qué distancift-&orre en el tramo DE? ,,ifl'
--',: ¿- a
A)x,.-30m
C)x=-20m
E) x.. 0
A) 5 m/s
D) 8 m/s
!^, u #, ,6,, * DIiC) &mt /=4I
D) 9m E) 10m
ll. Un autdmóvil que tiene MRLV recorre 26 m en el octavo
segundo y 30 mehos en el noveno segundo. Hallar la aceleración
del auto, en m/#.
A)s B)4 C)3
D)2 E)1
4. Un ciclista que tiene MRUV inicia su movimiento en el punto'4",
recorre 14 metros en el quinto se5¡undo de su movimiento y 20
metros en el octavo segundo. Halle la velocidad inicial en '4".
15. Un automóvil que tiene MRUV sale con velocidad inicial diferente
de cero y aceleración de 4 rrls2. recone 80 m en 4 segundos.
Halle la velocidad final.
A) 12 m/s B) 20 m/s C24mls
Dl25mls E) 28 m/s
A24,6m
D)30m
ts126,5m C)28 m
E)32m
B) 6 m/s
E) 9 m/s
C) 7 rn/s
lTú, Tienes.el Potencial. Nasotros lq Experiencia-.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-71-320.jpg)
![rI§ICA I ACADEMIA GALILEO
16. [Jn avií¡n se encuentra en reposo. ¿rntes de despegar recon'e 2 krn
en 20 segund<¡s, con MRIJV. L()¡ál es la velocklad con que
despega?
A) 100 m/s
D) 200 m/s
17. Un ilulo parte del rep«rso con ¿releración constanle. Si fiene
MlttJV y rccorre 34 rn en el novr:lro ser¡und o. i,ttrué ciisl¿tr¡ci¿r re
corc en el d<¡ce¿tvo sa1¡undo <le srr rl<¡virni<¿nt<¡'?
13) 120 rn/s O) 180rnis
[.) 2lj0 m/s
t3) 116 rn
I:) 76m
B) 182m
Ei) 100m
C) fi6 rn
ltJ. Lln móvil se despliua con MRUV y rccorre en el tercer segundo 16
m menos que el recorrido en e[ §éptimo s€gundo. Calcular la
aceleración del móvil, en rn/s2.
c)4
A) 46 nr
D) 66m
A) 192rn
D)i80m
19. Un móvil que tiene MRtJV.sale del reposo y recoue 100 metros
en el heceavo segundo de su movimiento. Detenninar la distancia,..
que recorre en el intervalo de tiempo t ,,' 4s y t ,', 8s.
Al2 B)3
D)5 E)4.5
C) 190m o/;,"
i
[-os exhemos <le un tren de 42 m Cg.X¿irü*.pq*ái por et cosQdt
de un "poste de luz" con velocidadedh y i$imÉ. r.ipe"u"ug Ste.
20
I.lallar la aceleración del tren, en m/s{{¡r;';r '.rt:'
f3)2 C)3
I:)5
i
:t",:<rar:.:
A)'I
r))4
.¿l lln ¡ní¡vil que liene MRUV.;iecone "d" nptros. par{iendo dql:
Nr¡roso drrrante cierto tiemp<i "f", pam tue$íiitiórrar 6.t1CI m,rfát:
¡lur;rnte los 10 segunáos si1¡uieriidiur'iogqndo .iiipliqár 'sü
, r.Lxridatl. I'latlar "d".
22. Un auto que tiene MRUV sale det reposo. l.n el ,noveryro: eegundo
recorre 5l m de distancia. eQué die{ancia recor're eri-eldg-cgavo.
A) ,ii5 nr
I)) ftijm
Al lOs
{tr&*
A) 2m,4m/s
C) 3 m,3m/s
E)4m, 1m/s
A) 4mls
D) 2,5 n/s
I3)"65m C1"75 r¡
E) 89m .l
B) ZOs
tr)354
c) 30'it
B)6,m,2 mls
Ol - 3 ¡r¡,4rd¡
B) 4m,2mls
D) 2 m, 1m/s
A)59rn ll)69m C)7-9sr
D)89m l-)99nr
ffi. tr)es autos A, y B que iie.npn MRUV salen
simultár¡eamente en el rnisrno sentido, del mism<r Ílu$to. coÉ
Fceleraciones de 2 g 4 m/sz. res¡rectivaanente. aDespués de qué
licrnpo estrrin separados 900 m?
84, tfu partícula que tiene una posieirr a¡ * '8 m .sq r,auÉv€ con
§ffiU hasta la pcición xz =. 'b 2 r¡¡ eü 3 s, S!¡ dpÉdar¿Biento St
,sr* rapidoz son respectivamente' :
A) 6 nr,3 m/s
C) 2m,6mls
E)-óm,2mls
?i...,"
E§. 1¿ posición de un móvit está representdo pEr la eeuacidn x .= 4t
* 2, donde x está en metros y t en segundos. I-a.fisieién inicial y
la rapidez del móvil son:
26. Dos móviles A y B parten simultáneamente de un mismo punto
en la dirección "t' x. Si el móvil A tiene la rapidez de 5 mls y cubre
la distancia dé 500 m quedando 100 m delante de B, équé
rapi&z ti€ne el móvil B?
C) 3 m/s
27. l.os méviles A y B van en la misma dirección con MRU cuyas
rapideces son 25 m/s y 10 m/s, respectivamente. Si A pasa por el
punto '?" cinco segundos después que [o hizo el móvil B, el
tiempo que tarda A en estar 550 m delante de [J es:
B) 5 m/s
E) 2 m/s
Ubícanos en la Av. De la Cultura7076 (frente a Ia UNSAAC)
37
C) li6 s
28. tJn móvil se mueve rectilÍneamente con v¡d<xidad dc | 50 mls. SI
entre t -', 0 y t ,,. 10s, la r,¡eloci<lad se reduce a cero, icuál fue la
aceleración media durante cste Inferv¡rlo?
A)40s
D) 30s
Al .Zmls?.
I)) 5nr/s2
A)ü,215 m
Dl0,125 m
A)0,90m
D) O,BOm
Bl2'l s
E)25s
PROIU.F:MAS Dr: CAIDA I-IBRE:2OO9
2.9. Llna ¡:artícula es laruada lracia arrit¡a desde un cierto nivel
horizontal. Determinar dmJrués de quá tiempo la partícula se
encnnhará 25 m clebajo del nivel de lanzamiento, alejándose con
velocidad tle 30 rnls. ¡¡ .. 1O m/*.
A)5 sB)6 s C) 7 s
l))8sF.)9s
lJn piloto suelta una bornba desde un helicóptero estático en el
aire, y después de 120 segundos escucha la detr¡nación. Si h
vek¡cidad del sonido la suponemos com<¡ de 300 m/s, hatlar la
velocidad de la t¡omba al tocar tierra, 9 -, 10 m/s2.
A) 1200 m/s B) 600 m/s C)300m/s
D) 900 m/s E)N.4.
fl Zrnlsz C) -liml#
I:) 1l¡0 mlsz
:
Lr los
B) 0,250 m C) 0,275 m
E) ñnguna
B) 0,95 m C) 0.98m
E) 0,7Om
31. Un paracaidista, despuás de s¿¡ltar de un helicóptero eshático en el
,,,,a:r:e, ffiJ5 ''rii sin, fricción. Cuando se abre el paracaldas,
",. adqgiffi:ü¡ia de.5ac€láración de 2 r*l*, tlegando al suelo con una
lu. iCr¡ánto tiempo esfuvo el,paracaidista en el aire?
i813stl)15s , ..:=,
.,D)
1 8sE)ZQs..,::,,':.
r_: j :,jri;. ;.;:.;: ..::,:.:..
3¿;.[1 ,t9¡o** sube a la velocidad constantp de 4 m&;
t:,li,s,i$.#g§e q-¡¡$?ñtra a 4o nr del .piáó; €e. §¡dE *¡¿a be¡ilsa dp
,,''tt"W:M: üempollegaráalpiso?g;i+';'[&w#
,4¡1,ff$§':,§:,:,,
,,-.: Bl 3,?Á s , ü¡ A,ffi *
&3. Uraa.piedra se lanza verticirfmente hircia.ar;iba desdp al techo de
rrr ¡ un á<iificio con unq,ve&xfrlad ¡nicjal.,Sg"C-0,d$r sftü pidh $€,
',. ,' deia'+aer 4 §egund<» dep¡és- q1n"sa ltt ksrAd¡r"h,l,{{B$&.
j,f H&r q.tur_4p en que, @qpués d¿ s& h dffi*m*b ,m.
' encuentáü.qinba a ta rñilffi¡á óga, g -, 10Wi,#.
A) 2s ,1 B).4s C) 6s
Dlt§tf,-,5-,s
I)],&s EliNingr¡na
B)120rn gES&r
E) b§nguna
35.' Una partícula que es dejado cap.r {eeotrr€ 55 rn er¡ el ¡rnírhinro
.'' segund<> de su caída libre. áDe qué dlum se,sd&6,(t,e¡.B&o? $ -
1O m/d
Alt?&n B)17&n C)200m
D)245¡n E)300 m
36. Det techo de un asc€nsor de 2 m cle altura se deqprende un elar¡s
en el insta¡te mismo det arranq!¡e del asrrnsor que sube con
velocidad constante de 1 m/s. Calcular la disfanc.ia a que estará el
clavo del piso del ascensor 0,5 segundo &spués de iniciada la
subidag*9,8m/s2.
3¿t,,&.;,i!s:gq{,¡ffi.piedra desde d reposap s.e qhsagr.e qge es tm
.,,- .& {ffid;É segr¡sdoc e su eaÍ& r€ssasa , ,¡s. dDEd*rÉi 'fu.sp
i= . 'sia&6#{euarpoag.: l0,Brii*.
Unas goias de agua salen del orificio de un tubo vertical con el
intervalo de 0,1s y caen librernente sin v&idad inicial.
Determina¡ la dhtancia enke ta primera y la segunda gota pasado
1 segundo despu& de salir la primera gc¡b, § = 10n¡1s2.](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-72-320.jpg)
![fa'(}alflery.4a *ii¿.
38. Una piedra es lanzada verLicalmente hacia arritra con una
vekxidad de 30 m/s dr¿sde una altura de 80 m. r,Cuánto tiempo
tardará en tocar el piso'? g '.. 10 m/s2.
GTIUFO GALILEO
A) 1,21 s B) 1,41 s C) 1,53 s
D) 1.73 s E) I .81 s
Una pelota se lanza verl.icahlente hacia arriba con una velocida<l
de 10 mis. ¿AI cabo de qué tientpo la pelota poseerá una
velocidad de 40 m/s? (g .,. 10 m/sr).
C) 5s
C) 6s 48.
49
39. De la llave de un caño malograclo que está a 7 ,2 m de altura cae
una gota de agua cada 0,1 s. Cuando está por caer la tercera
gota, se termina de malograr el caño y sale un chorro grande de
agua. áCuát deberá ser [a velocidad con la que sale el chorro para
que alcance a la primera gota, en e[ momento preciso que ésta
choca con el piso? g .= 10 m/s2
Una piedra se lanza verticalmente desde un punto A con Llna
velocidad de 80 m/s. iA qué distancia de A se encontrará un
punto B, en el cual la velocidad de la piedra será 20 m/s hacia
abajo? (g ,- 10 m/s2).
A) 2s
D) 8s
A) 1;B m/s2
D) 2.4 m/s
I3) 4s
E)10s
B) 2,0 mis Cl2,2 mls
E2.6mls
B) 98;20s C) 49;5s
E) 98; 15s
Bl2 s C)3 s
E) 5s
A) 3s
D) 6s
A)100m
D)320m
B) 4s
E) Absurdo
40.
4t
f)esde el piso se lanza un proyectil hacia arriba y retorna al punto
de lanzamiento, al cabo de 8 segundos. áCon qué velocidad
retoma al punto de lanzamiento? (g '- 10 m/s2) .
A) 10 m/s B) 20 mis C) 30 m/s
A) 0,90 m B) 1,00m C) 0,95m i
A)5m
D)25m
Un cuerpo es disparadó'Úerticalrüente hacia arriba con una
velocidad de 98 m/s. Si la altura alcanzada por el cuerpo coincide
con la del edificio, icuántos pisos tiene el edificio, si cada piso
tiene 5 m de alhrra y que tiempo demorará en volver al piso? (g
= 9,8 m/sz).
A) 49; 10s
D) 98; 10s
Desde el piso se lanza una pelota verticalmente hacia arriba a
rarón de 20 mls. iAl cabo de qué tiempo como máximo se
enóontrará a 15 m de altura? (g "= 10 m/sz).
A) 1s
D) 4s
50. Desde la azotea de un edificio,l& 80 m, uná..p.qf§ona suelta una
pelota de fútbol con la inte¡1"ción de agarrar''diéha pelota; otra
persona distante 20 m de ffiase del edificio'$resentando un
MRU, se dirige hacia et luffiirrdel impacto.
-ú€uál
debe ser la
velocidad V para que logre su;propósitg? (g -* 10m/s2). Desprecie
los efectos del aire, ,
t.:t
.:
B)200m C)300m
E)360m ..sr:i i, rr,¡:.-
20m
B) B m/s
E) L0 m/s
C) 4 m/s
A.
B.
C
D
D) 40 m/s E) 50 m/s
Un cuerpo se suelta a una altr:ra de 100 m. ZCon qué velocidad
llegará al piso y en Qué tiempo? (g =. 10 m/s2)
20.6-¡,; JzA.-
2016*¡.' 2.6,
1OrE -r.' ú0,
516 *¡r, 2.6.
E ZJi ^rc;3''6.
.41*,,,,..
Una pelota,cae verticalmente al piso y rebot+-Úñ'á#ñ# locidad
justo antes del choque es V y iusto después del cho${á,,r.4§t0,pV.
Si la pelota se deja caer desde un metro de altura, áa q$;{$y¡q
ttegaráclespuésdelprimerrebote?(g.,.9,8m/s2).
i,iiF
,liA) 6 m/s
''' D) Sm/s,
43.
D) 0,85 m E) 0,81 m
,..riniil¿;,,
;$a'-"""''iiiÉij=
Se lanza un cuerpo verlicalmente hacia ¿rrriba desde tierra co¡
una velocidad de 4O m/s. uallar después $.g,Oué tlg1no 1ffi€
altura se encuentra cuen l§g velocidadl.l de':10 m,b hacia
abajo. (g ' 10mis2).
A) 10s; 20 m B) Ssl 75 m
C) 5s; 2oom .'i' D)1os; 75mii';,,-.
E) 8s;120m i,
.,'; .,r,"' :,,.,:l
Un paquete qÉiiud" a 70 m del piso es'iarrzado verticalmente
hacia arriba cii¡ Vo =' 2O mls. Determinar a qué altura se
1
enconlrará luego de 6 s (g : 10 m/s ' ), ,
BI#fu=- .,,,...,.§fl5*
E) 35m "]. ,, . r'. ,
,:: :,,
"u
ffil'Dn.d" la azotea de un edificio de 80 m, se suelta un cuerpo. luego
,,ri,' de 2 s se lanza verticalmente hacia abajo otro cuerpo. Si ambos
llegan simultáneamente a [a base del edificio, calcular con qué
rapidez fue lanzado el segundo cuerpo. Despreciar los efectos del
aire, (g =' 10 mls2)
A) 35 m/s ts) 10 mls C) 30 m/s
0)60 m/s E) 20 mls
52. Una esfera se deja en libertad desde una altura de 80 m y al
rebotar en el piso se eleva sólo hasta la cuarta parte de Ia altura
anterior. cQué tiempo ha transcurrido hasta que se produce el
tercer imPacto? (g = 10 m/s2)'
53. Dos cuerpos "P" y "O" se colocan en la misma vertical tal corno se
indica en la figura. El cuerpo "P" se lanza hacia aniba con una
velocidad de 60 m/s y en el mismo instante "Q" se deja caer.
áDesde qué altura "x" se tendrá que dejar uQ" pará que ambos se
encuentren en la máxima altura recorrida por "P"? :
i
A) 4s
D) 9s
A) 450 m
D)210 m
B) 6s
E) 10s
C) 8s
45
Ix
I
46.
47. Un cuerpo se lanza verticalmente hacia arriba con Vo -' 30 m/s'
¿Al cabo de qué tiempo asciende la última tercera pade de su
altura máxima? (<l ,-., 10 m/s
2
¡.
B) 360 m
E) 870 m
C) 620m
@0 /'
#"
'ti" , .. El ¡Tú Tlenes el potencial. Nosotros la Experiencig...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-73-320.jpg)

![7 '"ffi''iJ
&csde¡:ria G"*¡.lile*
.{e. eii¿
entre cada piso es 7m. (lalcular al cabo de qué tiempo estarán
separadas las piedras il m. f)ar como respuesta el tiempcr mínimo.
(o ', 10 m/s'z)
A) 1s 13) 2s
D)4s I:) 5s
$RÜF$ GAT-IL§O
Desde un globo aerostáLico que asciencle vertic¿rh¡erfe con una
rapidez conslante r1e 1.0 nl/s. se lanza un proyi:ctii en fonna
horDon1al con respecto al glot;o, con un¿) rapidl'z de 5 rn/s,
cu¿rndo éstc se hailatra a 40 ur del pisrr. ¿(luál será el av¿lnce
horizontal obtenido por dicho proyeclil? (g ,.. 10 m/s2)..
67, Dos esferas salen rodando de la superficie hoúontal de una mesa
con rapidez de 3 y 8 m/s cayendo al piso. de tal rnanera que sus
velocidades forman ángulos conrplementarl<>s co¡r el piso.
Calcular Ia altura de l¿¡ mesa. (gi, ,10m/s2).
c) 5m
[Jn proyectil, una piedrti y un carro parlen al mismo iiernpo de los
puntos A. R'y O respectivamenfe. Sabiendo que cuando la priedra
y el proyectil chocan en "P" el carro pasa por "A", halle la ral"ridez
de lanzarnientó del proyeclii, si [a piedra y el carro parterr del
reposo. (q ... l(lm/sr).
C) 3s
C)1.2m
71
A)20m
D) 15 nr
N:.2 mls2
B) 5 m/s2
A) 5 m/s
D) 10 m/s
B)25 m
E) ll0 m
68. Por un plano Inclinado de 45'se lanza una bola con 1a rapidez V0
y formando también un ángulo de 45" con [a horizontal. (No
considere rozamiento).
Calcular el valor de L.
()
ó
t3 L =V?'o
A)'5:... &=
D)20'ml5
De lo alto de uriá],:,lórre de 16 m de alfura, se lanza un "hueso" con
iuna rapidez de.:20 m/s formando un tin¡¡rlo de 53" por encima de
{á1;hqrizontal. Determinar la aceleración constante con que debe
@treii,uopbrro, a partir del reposo y qu€ se encuentra al pie de la
torié¡,:ijara que puedar ¿rlcanzar el "hueso" cuando esté a punto de
tocar,Ül suelo, g,.10 mis2.
A)0,6m
D)1,6m
A) 2,5 s
D) 0,7 s
t3)1m
[:)2m
I"
B q v"...0
80m
B) 10 n/s
l)) 2!> mls
B) tl m/s
l:) 15 m/s
C) 15 m/s
B) 3 m/s2 Cl 4 rnls2
E) 6 m/s2
V.
A L-.- "
eoó
. ¡., [Jna masa muy pequeña es Ianzada hacia la pade superior de un
plano inclinado como se muestra en la figura. ZCon qué rapklez-,
en m/s, debe de.jar el plano para llegar justo al punto I']? (S -- 10
m/s2)
v).
^foL-. f, --
)o
V1 -,:,- r _ o,.:
D. l)---=-
1o
.. v''
E. [,# "
',..{
:r
69 Si la altura *a*iÉ-.sl"f proyectil mostradFnn la figura es 12,8 m,
áqué tiempo t"iaÉ,i,-
lfe.l1B.?,!.g¡10
misr)
;i|l')
C) 2 rnls
c) 1,6 s
E 260Jim
Un avión vuela horizontalmente a 540 km/h, y a una altura de 98
m sobre un barco que se mueve a72l<tnlh en la misma dirección,
iA que distancia del barco, e[ avión debe soltar una bomba para
hundir dicho barco? (distanciar respeclo a la horizontal).
36oJsmA
B 26rJim
c zsslirn
262Jim
74
B) 0,9 s
E) 0,5 s
-__-_____-/,/tr./,/r./.(.r,
. :lll
I 7ú . ¡Tú Tienesetl'otencislNr¡sotoslaExperiencia.,.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-75-320.jpg)


![88. t-ln aul<¡, y vertic¿llmenle por encirna de é1. un avión; avanzan
paralela y reclilínezrnienle con 20{) km/h <x¡n respecto ¿l tierra.
Brusc¿rrnente se paran lt>s motorcs clel ¿rvií:n, rlue ertlort<:r:s
corli¿¿nz¿r it ca<rr (tir:spret:i¿rr rt¿sisttzt-t<;i¿t rk:i;rire). Iiltlotlccs:
A. I:l avión toc¡t lit:rr¿r dtrl¿¡tlltl del .ri¡lrt¡.
IJ. l:l ¿ivión ciierá iuslo s()t)re ?rl .rtll().
O. (lu¿rndt¡ el ¿rvi<in lc>c¿i lit¿rt.t. ¡ror tiit:lio ptt:tl<; y;r Ir.r'i(i ei
i.¡ulo-
D. I-a respucslzr delxrnde de l¿r ¿,lltlr¿-, cle uu¿rlt, rlel ;¡vróll
I:.. I-a respuesla delx:ntle <le l¿r tn¿rs:t del avr<in.
89. l.n el instante en que Llrla ¡lied¡a es soltarl¿r des<le el punlo A' un
proyectil es l¿rnz¿rdo dr:l pr"rnto ll con utr¿r velocidad inicral V¡qrre
form;r un ángulo "úY " con i¿r horizontai. I)elermine el v¿rlor de "
A " pittirr¡tttt el proyet:til Im¡r,rt:lc ir lir ¡riedt;t ett el pttlllo I)
A) 30"
D) 60"
B) 37' O) 45"
I.:) lr3'
¡'t) 0.u s (l) 0,75
l'.) 1.25s
90. I:l carrilo acelera con a,,'1 .!> m/s2. l)esde el punto "A" se§uelta
un lornillo. ZAI catx¡ de quá tiempo ch<¡ca con la'-üperficle
eslérica de 2,5 m t)e. ra<lkr? (g' 'i0 rn/s?), . .,,,"'''' !
91.
f
A) 0.6 s
D) 1s
(Jn estrrdianle. p¿)ri) m(rdir l¿r ¿rllur¿r dt' un árbol- lanzá una piedm
desdc una dis'lancia horiz-onkrl de 42 rnrmediante rin apááto
desde el suelo con un ánqul<¡ de elevabión de 53". Sirél coq§.kr:tat:
que el tiernpo tr¿rnscurrido entre elrdisparo y la ltegjádá..idé':lg...l
piedra a [a punlar dei ¿i¡bol es í3 s, ¿.cuá[ es la ¡¡ltt¡rr (gnrnietros]li
del árbol? (Asumir g , 10 m/sz)
A) 7m I)) 9ur
D) 9,6m F.) 15m
C)11m
92 I)e una manguera t¡roi¿:n ch<¡rros <le alua bajo 1ps ángutos I y
p respectct al horizonte, con la misma rapidei iniciá Vn. iA qué ¡
'dist¿rncia con respccto a la horizontal los chorros se intárcepta-qf.t: ¡
p'
2V2
A)
B)
r':
J|::
g(tan 0 +tan B)
V,
g tan9
llbícanos en le Av. De la CultiraTATe
'ffrenie
a'la UNS'AAC)
§Ígrq*r ,,--- Ac6BEftrIAGltLILRg
V?-
C) x'=
gtan {)
L')
g (lan íl i
t '(tan?
I;, .-
g larr //
(Jn proyeci.ii, en movimie¡rlo parabólico pasa por los puntos A y
ll. I.a figura ¡nueslr¿l la rn;rgnitud y la dirección del vector
velocid¿rtl dei yrroyclclil en dichos puntos. Diga cuáles de las
si¡¡uienles ¿rfimlaciones son verd¿rderas (V) o falsas (l--) en el
misrn<> <¡rtlen en que son t¿nunciatlas:
[. f-ll tiempo r¡ue la«1a el proyectil en ir del punto A al punto B
es il,li s.
II. [ -a velocidad del proyectil e n el punl.o B es de 75 nr/s.
Itl. La dist¿:ncia horizontal entre las proyecciones verticales de
los punt<>s A y 13 sobre el piso es de 210 m.
(()<¡nsidere q, l0rn/sz).
trn /))
) La!1
t
t tLt]nlJ
93
§s¡§§§§
1l -r-;;;
too,,/..Ú--'-'
t',t A 51"/L /-.t - *
,... t.:. ....
:';;l:,;:,,;,;;r. IIOriZOntAl
I
En é1, inst¿rnte rnostr.adé, tres esferas 5$¡ puestas en movimiento.
Si déáprrés de I s la esfeta B eluidista 10 rn de cada esfera
cuandol1as tres se encuentmn en la misma üertical, determine la
f/
/,.
relación I si es m¿ry()r que i.
t,,
A
Qv:o
Un zancudo, por efecto d¿ insecticida empieza a volar en círculos
sobre una mesa horizontal. como se muestra en la figura.-Sl
suponemos que partió de "Al, en sentido horario y que cada
círculo descrito tiene como diámetro el radio del anterior,
ocurriendo esto dürante 3 minutos hasta que el zancudo muere,
5
ffi
$?
7
C)
D)
A),WV
D) FVT
r !:.
ti) tr¡;1: c) vFr
t") vl'l
94,,
B
r->
ig
J4r
5
Jn
7
A)
B)
&7
5
lr)
95.
N§¡§)N¡](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-78-320.jpg)

![FI§ICA I ACADEMIA GALILEO
L
I
A) 60 radrs
D) 150 rad/s
del borde del disco
A) 104 cm/s
C) 8z cm/s
E l2n cmls
Al-2,22 7r
Dl-2,52 /[
A)1,8
D)1,0
A) 0,75 radis2
C) 0,80 rad/s2
E) 1,25 rad/s2
B) 180 rad/s
D) 30 rad/s
tti| 9/r círl§
D 6¡r c¡ili
8-3,33 7t Cl-2,77 7t
E)-3,42 7t
i xl:iir.
:T ritrllil
C) 210 rad/s
105.Si el cenho de la llanta "A" se mueve a 30 km/h. halle la rapidez
del punto "8". El radio de la llanta es 15 cm y RC :7,.."¡ii-
A) 16 km/h ts) i4 km/h C)30km/h
D) 34 kmlh E) ¿.4kmlh
106.Un disco g¡ira a 45 r.p.m. siendo su radio de 13 cm. Halle et valor
de la velocklad tangencial de un punto qu"., nn.r"ifiriiái'7
"-
107.1-a velocidad angular de la hélice de un motor dqsclende
uniformemente de 800 r.p.m. hasta 4O0 r.p.m., efectuando en ese
lapso 60-revoluciones. Entonces [a aceleración angular, en rad/s3,
que experimenta la hélice será:
108.Una polea gira a 360 r.p.m. y llega al reposo en 10 s electuando
un MCUV. áCuántas vueltas efectúa en los 2 últimos sequndos?
B) 1,5
E) 0,9
cl1,2
lO9.Hallar e[ módulo déla aceleración angular de un disco, si al cabo
r
d* V3 segundos de iniciado el movimiento uniformemente
acelerado, la aceleración de un punto periférico del disco forma
37" con la velocidad lineal del mismo.
Bl2,25 radlsz
D) 0,25 rad/s2
Ubícsna§ en Ia Av,. De la Cultural0T6 (frente a lo UNSAAC)
110.Un cilindro vació de radio en su base 0,4 m gira con velocidad
angular constante a 1li0 r.¡r.s. respectt> a su eje vertical. Se
dispara un proyectil horizr¡nt¿¡lmenle. de nrodo que pasa por el
eje de rotación. Calcul¿rr la máxima velociclad del proyectil
(constante) para que alr¿rviese al cilin<lro haciendo un soür
agulero.
A) 200 m/s
D) 280 rnls
C) 240 rn/s
ll1.Flallar la aceleración angular en md/s2 de una polea sat¡iendo
que, al c¿rbo de li s de comerzar su movirniento uniforme
acelerado, el vect<¡¡ aceleraci-ón de un punto que se encuentra en
su periferie forma un án5¡ulo de 5ll" con la dirección de la
velocid;rd lineal de esle mismo punto.
tsl 22O nls
E) 300 m/s
1
J
A)-
4
4
D)
-75
4
ts) "-
a
J
2
E)
-3
a
J
c) -
75
112.Un disco rota uniformemente alrededor de su eje. Los puntoo 1 y
2 distan 2 9 4 cm respectivamente desde el punto O. [,a razón del
l"^ )módulo de las aceleraciones de los puntos 2 y 7, I i L r"
at ),r
::::: .t :l
entoilÉi1s:, ,
A)1
D)4
r3)5. C)3
e)2
U3,D9.i,t¿ii'slqui¿ntei¡u.p afirmaciones es correcta:
,A. . . Lá.zrcelerácián tangencial siempre tendrá la misma dirección
, .',,,4pg.fu.velocidadinstantánea.
' ' ts. SljIá aceleración tangencial es cere, entonces la velocidad
' r instantánea mantiene constante solo su módulo.
: .'Cr 'Si un móvil posee aceleración normal con magnitud
.., ,'..,' constante, entonces se hstaÉ de un mor¡imiento circular
' uniforme.
D. Si la velocidad es cero, entonc€s la aceleración también ¿s
cero.
E. Ninguna es correcta.
A)A B)AyB
D) Solo B E) Todas
C)ByC
114.Un cuerpo se mueve sobre una circunfereneia con una rapidez
constante igual a la quc adquiere cayen& ]ibremente desde una
altura lgual a la mitad del radio de la circunferencia. áCuál es su
aceleración cenkípeta?
A)
g B)2g
7t
?o
D) g ort
.i if](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-80-320.jpg)
![r
ffi,&"raá*s:nry^**W GRLrpo GltLtrLEo
La estática (F-statikos ,.. Equilibrio) es parte de la mecánica de sólidos que estudia las condiciones que deben cum¡rlir las fuerzas rlue actúan sol¡re
un cuerpo, para que áste se encuentre en equilitrrio.
EQUILIBRIO.
Un cuerpo se encuentra en equilibrio cuando carece de todo tipo de aceleración. Existen dos tipos de equilibrio:
. Equilibrio estático (estado de reposo). v=0
. Ilquilibrio cinético (estatlo de M.R.U.). v-'cie.
III,]ERZA.
Es una magniiud física vectorial qLre nos expresa la medida de [a interacción mutua y simultánea entre dos cue4]os en la naturaleza.
UNIDAD DE: MIiDIDA. 'rii?'r,.:, :,'=
[f = nxal: lkgm I s2 = 1 Newton (N) SI .,,':'
lf ."mal.=Tgrcntls2-=l clina(.d) C6,S 'i.,,-
i Newton = lOsclinas.
MA§A. ,".:,.: llii '- rriiilii'.
Es la nragnitud física escalar, que sirue para me<lir la cantidad de inercia que tienen los cuerpos."[¿ ] = kg , Si.
Es la fuerza cie atracción gravitatoria que ejerce la tierra sobre los cuerpos:dlJ,tp*pe encuentraliih sr¡éj'inmediacioneé
iiili'i i-t':i
i,i:i::.
Primera condición de equilibrio. Un cuerpo de masa constante m estará
""
*ü"if¡Uti. de traslación si la fueza.resultante que lo afecta es
igual a cero. ,+
4 =Ó' É.=- ;.,1'-,ñ:ffi¡¡.Q.....9) G-.,1';,F-,¡=io.o,ol
* ,r ,TEOREMA DE LAMY. i!1,
Si un sistema de tres fuerzas concurrentes y coplanafá ?iiün,sobre ún cue$.ÉiáÉ#ilibri e cumple que el valor de cada una de las fuezas es
directarnenle proporcional al seno del ángulo opue.'' , ' .,t-
P
====r--gill¡
nr
=-., - =
F3
sencr-.'éenB sen0
Irz
:i::i;r:.z
una fueza para hacer rotar o girar a un cuerpo sobre el cual actúa, en tomo
o: Centro de giro.
b: Brazo deFuena.
UNIDADES DE MEDIDA.
* lM = F.b7= N.m s.r.
* lM = F b)= d.cm ccs
Líneade _
ación de F
-tr _.
- ', ,; t¡-l ¡Tú TieneselPotencial.NosotroslaDxperiencia,'..!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-81-320.jpg)


![FI§ICA T
lirE%
ACILDSMIA GALILEO
4R
x,---r7t
PIIOBLIiII,/I NIIO: l:l :t-l:-
Fin la figura se muestra una barra homogénpá de peso W. La pared
vertical es lisa. Calcular la distanci¿r X para que el sistema se enct¡enke
a=7 €
Rpta :d ."'j; r,
Pnlllll.llUA Ilt0: I I
Llailar la tensií¡n en el cable en Newton. si el sistema está en equilibrio
y la placa homo5¡énea pesa 9rrN.
en equilibrio
Rpta:
l¡R(»lLliMA NIl0: 14
Si la esfera mostrada err la figura pesa 14 N. Ilallar el v¿ilor de las
fuer¿as de reaccií¡n en los puntos de apoyo A y [3. o.,37o
i"
i
' .:'.. ' ,
Rpta:-lrr-; 12hl
Plt0lll,D,llrt NR0: I2
(Jn espejo de l3N rle ¡reso. cr.¡y() iargo es el doble que el ancho,
cuelga de dos crrer<las diferenles como se muestra en Ia ligura.
Encuenlre la mag¡nilud de la fuerz;l l- necesaria para mantenerlo á
esa p<.rsiciórr.
i
t
r=Ff
Ubícanos en la Av, De la Cultura7076 (frente a la UNSAAC)
Rpta: R ,,. 55 N
I{Pta:Rn=4ON - Hn=30N
Irlt{}lr¡.¡i.11.,1 i'itt0: I 5
I;r placa cu¿r(lr,r(1il lxrnroqérrea tle la lir¡rra se encucntra en equilibrio
apoyada en una superficie ¡:lana rugosa y sujctada a una pared
vedical mediante r¡n¿r cuerda, si l¿r raz<in del peso W de la placa a la
tensión de [¿r cuerd¿r es de 8 a I]. áQuá valor tiene
RPta: P = St'
i
Plt0BllillA Nlt(l: l(i
Se tienen tres esferas iguales. de 60 N de peso cada una y de 20 cm
de radio. Si la longitucl de la cuerda que une a 13 y C es 24 cm. Hallar
la tensii¡n de la cuerda en N.
: .;,,;;,,..:;::.:;:, ,,, Rpta: T-4ON
pnoBir]Eí"ñ*o: lz i .
Una barra uniforme. de peso 100 N, esÉ suj€h¡da mediante tres
cuerclas,,corno se aprecia en la figura. Si W -2001¡ y 0-,l3".Cakula¡
el valor de las tensiones €n:[ás cuerdas 'l'1,
T¡ y 13.
,'.: Rpta: T, .,,100 N - Tz .' 150 N - 1.i .,250 N
Pll0lll,llllÁ NllO: lf!
Una persona de 80 N de peso se encuentra parada sobre una
plataforma de 30 N de peso. Si el sistema se encuenka en equili5rio y
cada polea pesa 10 N Calcular el valor de la reacción de la
plalafomra sobre la persona.](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-84-320.jpg)
![f+.ca{'lgfllli{'.,, ;¿ tuco
PB0BLI¡üA Ntt0: rf]
C¡dcular la longitud de la cuerd;r que sosi.iene a la varilla de 2 m de
longitud y peso P ., 20N
T
Rp¡61 ¡...Jlrt
PBOIIIIIMA NBO: 2o
Calcular el valor de la fuez¿r horizontal I-' requerida para sacar de la
cavidad de la superficie. al cilindro.
rt-0 (l 31" P, 200N
+illr
iá¡R'= 150S'
son imponderables
a"//,/-2,/./"1,2z/.1z/-¿,..:i.1:a:::::r.!rl,r,.¡:r1::,i*:,i,:i;irlr,
: ::.:.:,#,ti l:
::::.::i:a:::,a-
Rpta: Q ,. 180 N
N y forma 45" con e[ eje
Rpta: a = Tg'1(14131)
Pn0BL[il^ NII(I: 2l]
l-lallar el valor de 0, si los trloques üenen igual peso
l¡ftOIl[IIMA NBO: 24
G$Lt'PO GAT.ILEO
Rpta:0 = 74"
mantienen €nUna barra de peso 2W y el blo$á de
equilibrio- Hallar el valor de q. jii
tu
(&
?-::
a:i;
,+ :;,i¡,.',.
,,.¡,1:.
u.i!Éi.gln¡,nun Nndi': "
i:tF.rF.?.r.ra mostradaifB es homogénea. I)etermine el ángulo que fomla
Rpta: a = 2(P
H:'4ip.e..l en gl éxtremo A con la horizontal
Rpta:0= arctgZ
PnOBL¡lMll NIIO: t{l
Determine la lectura del dinamómeko, si la fueza entre el bloqu€ de
1,9 Kg de masa y el piso es de 7N. (g = 10m/s2)
Rpta: 12 Newtqn
Pll{lBLlllEAñBO:2I
*}*i
,
Calctlar el valor del peso del trloque Q par¿) que ei sistema mo§ &;
se encuentre en equilitxio, sabiendo que P"..320N, y que las cuer@$l
' ' f t{ ¡Tú Tienes eI Potencial, Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-85-320.jpg)
![r
r"Ísrce r
:ry.|
ACITI}ETITM GALILEO
l'tt(llllJIilA NII{}: 27
Si el bloque pesa 20 N y las poleas son de 4N de peso cada una.
Hallar el valor de T.
1../_-1**
Rpta: T = 8N
PBOtlLliM¡r NII(I: 2tl
Si el sistema está en equilibrio, calcular [a tensión en el catrle ABC; la
bana homoeénea pesa 50N.
Ilpta: T.=,'150Ñr.r
t
Plt0BL¡lilltNlt{l:2$ ,'. .
Una barra de acero de 100 Kg de masa des<:ansa apoya<fa en'el pulto
C, tenienclo una masa.de 50'kg n" B, tal-::omo.ga-:ntuestra.-gn la
'Rpta: x = l8,I25m
: :'
PttOBLtilIANtr0: ll0 t:. ,,,,.,' ,'l
Calcular e[ valor de la tensión en [a cuerda AB que soporta lá'i&lurnna
inclinada mostrada en [a figura.
AC',,8m
CD"6M
CE -, 12m
P..,5N
Rpta: T = 6N
lJbícanos en la Av. De la Auhura7076 (frente a la UNSAAC)
Plt0llU]ilIrt NIIO: 116
Ilpta:lt, = 4JñN
PII()IILIi^IIA NL0: :ll
Hallar el valor de [a tensión 'f en e[ c¡rble. si las esferas s«rn de igual
peso (100N) y no tienen asper?zas. 0 -. 53"
*.,BLB,'IA NIt{}: Í}2
RPta: T = 2ooN
,,,.F-n la [rio. se muestra un r<¡dillo de 200N cie peso y diárnetro D "'
l100cm. Calcuiar e[ valor de la fueza "F" que es capaz de hacer subir
.'fel rodillo"A" sobre el rodillo "ts" cle diámetro d -. 25cm.
I:
@iI;:'rrr::: r: :
npth: F= lo6N- rfP
púlrnr,n,lrn rurl¡,i3'
Si:elSist ma esiá dá¡uitiUrio. qué distancia del punto A se encuentra
e1'punto de aplicaciórr,del pesq.de la barra AB?
c+10' B
Rpúa:X=7rL
PITOT}LETIA,NITO: 34
Calcular efvalor.dg-la.:firdza F necesaria para sacar una esfem de 30
cm. de'ta'{iq 9 45N:dé'peso de un hoyo de 12 cm. de profundidad.
Rpta: F = 39N
PROIILI]IA NB0: ll5
[-a bana homogénea AB uniforme pesa 12N. la zuperficie vertical es](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-86-320.jpg)
![7
.r:mcherrtia ünliIe*;!a ¡*á.t
!,ti{}llLlill ¡ §li(l: :l(i
llaicLll¿rr i;r krngiiud de la tr¿rrra, si est¿i en reposo y las tensiones en
i¿¡s errerci¿:rs A y 13 eslzin t:n rel¿rción de 5 a 1.
GftUPO GALILEO
l¡ll0lllltrllA Nlt(|: li7
[:n el equilibrio estático, la barra hornogénea pesa 200 N y el bloque
7l¡ N. I lallar el valor del ánsub 0.
r: 2.o ., l,
Rpta: I.=LOm
Rpta:0=53o
OI1IE,TIVOS:
^'o"o*rrr'";";."rd,";;;;;r',*nn
tu
"upu.iauo
a*' t
I
/ Conocer los conceptos de inercia y masa. I
r' Analizar la causa de los cambios de velocidad de un cuerpo. 1
/ Establecer la relaclón enke [as fuezas sobre un cuerpo y a¡ acelemeión.
r' Comprender las nociones básicas sobre kabqio rneciánieo decde el punt'o d€ vista de la Física. j
/ Conocer e[ proceso por el cual se da [a tran-cmi§ión de movimiento meeánico.
/ Deducir un concepto de energía, que nos pemititá dar e¡riplieaeión de lo§ feaómenos ffuicos.
,/ Conocer alguna3 iormas de energía que,se prentan en la na&¡mleza
,/ Establecer [a relación entre el kabajo y [a energúa mecánigq, y 9n funeióm a elio, poder reconocer en qué casos §e
t :-', cihética; durante, yr:dEsp-l¡És de¡
Es parte de l¿r mecánica que estudia Ia relaEiónenlre la fueza y el movimiento. t-a dinámica se basa en las tres leyes de Newton, quién
formula las leyes qú? llevan su nomtrre y que soa,'h base de la mecánica.
LEYES DE NEWTON DEL MOVIMIEhffO.
1. LF:Y DE I.¡q I§¡EBCIA. "Un cuerpo permanece en estado de reposo o en movimiento con v-.constante (M.R.U.), mientras una fueza
ext.ema n() haqa cambiar su estado ínicial".
2. SEGUNDA LF:y DE NEIIITON. Esta ley establece lo siguiente:"Cuando sobre un cuerpo actúa una fuetza resultante, ésta le comunica al
'
"uo,po
una aceleración de la misma dirección y sentido y el valor de esta aceleración es directamente proporcional a la fueza resultante e
inversamente proporcional a la masa del cuerpo"
& tErcEB&, LEV DÉ,![Eüɧú]É (tey de acción 9 rÉacció&]-. Esta.ley..e$@ry 1o siguienta"A toda fuerza d¿ acción se opone siempre una
luena de. reacción de [a misma magnitud pero de sentido conkario".
FUERZA DE ROZAMIENTO O FRICCIóN (f). Esta fueza surge cuando un cuerpo trata de rnoverse o se mueve a través de una
superficie áspera op6niénrlose a su cleslizamiento y manifestándose tangencialmente a las superficies en contacto.
Cu¿rn¿o un cuerpo se rnueve sobre una superficie lo puede hacer deslizando o resbalando y también rodando, en tal sentido tendremos:
f, = rr"Nr,,
-+-)
F
, , ,, ,,,",, ,.r,, ,.rn,,, , ,, ,-f66-l ¡TúTieneselPotencial.NosotroslaÚxperiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-87-320.jpg)
![f
rÍSICA I ACADEMIA GALILEO
FUEnz.h DE RozAurE¡rro rsrÁr¡co
( f; ).- Esta fueza sürge cuando la superficie rugosa de un cuerpo. intenta deslizarse sobre la superficie rugosa rle otro cuerpo. [¿ fuer¿a de
rozamiento estático es tangente a la superficie de contacto y se manifiesta en. dirocción contr¿ria al posible de
cuerpo respecto a otra.
de hr superficie de dkho
I
[.a fueaa de rozamiento estático tomará su máxirno valor, cuandq lá suprficie de dicho cuerpo está a punto de tleslizar respecto del oho, para
tal efecto s€ uliiizará:
lh fuena de fricción gstá fuertemente li¡¡ada a la aspereza de las superficies que entran en contacto. En las superficies por lo general:
P.',j l',,"r,.*ii
fUEnZA ffi kOZAüIENTO CINÉTICO (I.).- Es aquella fuezalqúe.girrge cuando la superficie ru¡psa de un cu€rpo desliza sobre otra ( con
velocidad constantle o se mueve con aceleración ) que también es rugosa. Esta fuerza también es tan¡¡ente a las superficies en contacto, y s€
opone a[ deslizamiento de una respecto de la oha
.'=-, -. '.t:,
N : Fueva como componente normal de la acción iieJ pi§o scjbrg e[ cuerpo.
, : ., ..r ,.
:;.:;. :ti.::t :: .:
GhÁrrc, oe res:rri¡Enz*3-I
f-
l
t
fiepessntffiióri gráfrca de la va¡iación de la fuer¿a de fricción en función de lá fi¡er¿s ¡nderru qlhada d cu*rpo.
Pc b gured se cunqle:
0,¡r" < p.. 1
f En algunm casos especiales ¡r. , 1 )
La fuer¿a eie re¡zamiento estático es variable y según el Lrloque de la fig¡rra. es del mismo módulo que la fuer¿a extema a¡llicada al bloque
üblmnax e* lu &t¡. üe to talural0Tí (frenre a Ia ANSAAC]](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-88-320.jpg)
![Acatle¡tria ii1{i}"q,* ,¡i'*,:i *s:
§EUFS GALTBE{)
@
Plt{}I}l,ll}lll Nl}.¡: llll
(.luanclo s<¡brt: un bloque tle 1() kg que se enclrentra sobre una ntesa
hr>rjzontai lisa actúan lzrs fuerzas F, ( 20 i 30 j )N.
F?''4Oi N; F¡ (15i I 50j)NY l1; ,laaceleraciónque
adquiere liene un nrírdukr de 4nls2 en dirección del e.je I x. Si sobre el
bloque actúan las fuerzas Fo y Fs -(25 i 6O.i )N, halle la
aceleración (en m/s2) que ten<1ría clicho bl«1ue.
pr.:
-a
,,, r, i ¡ i
t)lt0¡llBMrt Nlt(): llf)
En un laboratorio de rnechnica, ¿r diversos bloques con diferentes
masas que se encuentr¿rn s<¡t¡re u¡ra superficie horizontal lisa, se les
aplica una misma fuerza ¿r cada una de ellas, resultando la gráfica
adjunta pa:ra las aceler¿iciones medidas. Ilalle el valor de mi (en kg).
(k!r) '.,,'.
gRPta: mr '' 0,75 KS¡
::
j .+ 29k N, se aplican
sobre un bloque cuyo peso es -20k N. Si e-l,bloque,se,ryqeúe en el
aire, sin considerar la fricci<in, halle la:acelemcióñ,éq::íh/s2 que
adquiere el bloque. (e ,. 10m/s2.) ,t',t
, .
' .: .a:¡-:
RP@.¡'= 8,5 i'r- t2 j + 4,5k
l
Pltl)BLliürt Nll(l: 4l
[-a figura muestra dos objetos cuyas masas son m y M. Si m se
encuentra sobre una süper{icie lisa. Halle ,r, para que la magnitud de
PROBLIIMA Nlt0: ,lo
+
I-as fuerzas F, 17 1
la aceleración de la
gravedad.)
partíiula M sea 8 . (g: aceleración de la
3
+,
r 23 j Ny F2,..
+
W'rrrrr.lM
Frptat
t
=2
M
PBOllLlllIA NBO: 42
Una partícula de 2kg de masa desciende por un plano inciinado en
37" cuya long¡itud es 2 m. Si el tiempo empleado en llegar desde el
extremo superior a la base del plano es 1.. halle la fuerza de fricción
(en N) sobre la partícula.
RPta:F¡'" 4N
' I
f 9il ¡Tú Tienes el Potencial. Nosatros la Experiencia.,.!
l'Il()lllilllA §!t{}: 4l}
[Jn rnuch¿rcho c1ue pes¿] 25() N en rrna b¿¡l¿urza se pone de cuclillas en
e-lla. y salla repentínaimenle hacia atrib¿¡. Si la balanza indica
momentáne¿rrnente lili0 N en el instanle del impulso, l.Cuál es la
rnáxim¿r ¿rr:eleración del muchachc¡ en este proceso? (g ,,, 10 mls2)
Rpta:a .- l.2 m/sz
PlBOIlLli,lIÁ Nlt0: 44
Una persona de 250 N de peso, desciende por un plano inclinado,
sobre un carrito. l'lallar la inclinación del plano si su peso aparente
cuando desciende es de 160 Newton (g'-= 10m/s2.)
PBOIIIIIMA Nlt0: 45 '
Determine [a aceleracién
No LIav roZámiento
t;,-*,
: RPta:as - 1'2mli¿
PIIOBLIIITT NRO: 4li
A la polea de peso despreciatrle se le apliczr una fuezá de 200 N de
,nu.,áru qun acelera a razón de 1 m/s2 si m -" 10kg. Hallar el
coeficiente de rozamiento cinéticr¡ entre m y la superffcie.
(g - 10m/s'7)
,l
Rpta: ¡r". '
4
PROI|LüMA NR(} 47
Hallar la aceleración o, con [a que el bloque de masa m desciende por
el plano inclinado en 37o, si el ascensor sube con una aceleracíán gl2.
(s =" 10m/s2)
Rpta: q *9mí*
Rpta:O = 37o
bloque B, Si m¡ ,. ¡¡".
(q 10 m/s2)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-89-320.jpg)

l'll0llllirllÁ NIIO: 52
[Jn bloque se deslTa p<ir ei plan<t inclin¿rdo 37" que se mueslr¿1, si
larda 2s en llegar a la horizr>nt¿¡l. Determirl¿¡r el coeficiente de
rozamiento cinético. (g,.. 10rn/s2).
líbícanos en la Av. De la Cultura7016 (frente a la UNSAAC)
Rpta: p, , '0'5
Rpta: P. 'll8
PüOBl¡llilrl Nll(l: 5ll
Calcular I¿¡ ¿rc:eler¿rcitin der lTl¡ - si rnl l0Xg. y rn, . 20Kg.
Rpta:a=3.26mls
I,ll(llllliltl¡l lt ltt): ¡i.l
Si retiramos el bloque de rnasa "m" del sistema. tLn qué pcrrcentaje
variátá la acel<¿ración d¿:l sislem¿r?
Rpta: Aursentará er¡ 20%
PBOIIIDIIA ]tlt{l: §5
Un ascensor sube con una aceleración de 2§ r¡rs¿. Hallar el valor de
m2 en Kg. Para que mr-30 Kg. Se encuenhe en equilibrio con
Rpta: m2= 1S l(g
PB0IILDIIA Nlt0: 56
El bloque mostrado pesa 200N. 5i e[ coeficiente de rozamiento
estático entre el bloque y el plano inclinado es 0,37 y [a fuerza F ='
60N es horizontal. l,Cuál es el valor de l¿: {uerza de rozamiento entre el
blooue y el plano inclin¿ido?
RPta: f. = 72 N
PllOll[I]MA NllO: 57
El objeto mostrado en la figura tiene una masa de 0.5 Kg. Y se
encuentra a punio de deslizar. Hallar el valor de 6.
t)F1
s - iom/s2
3N](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-90-320.jpg)

![/
Acacleln i rr t-l :rl i i t' tr
-ta ,x:¿ 4:t«c"
PB{tllLBlIA Ntt(l: 7{l
ii, .i.torrro físico cual debtr ser el v¿rit)r de I-', t¿rl que los bloques de
nrasas 20 kg y 10 kg estén en reposo cc)r) respecto ¿ll canitr¡ de 90 kg
de mas¿¡. e 10m/s2.
Rpta: l/ 400J4 N
PrU)Bt,IlrUÁ NIt0¡ 7t)
l)<;s cilindros sus¡reri<lid<ts por una polea son atrandonados a partir de
Ia situación rnostra<ia en [a figura, áCuá¡rto tiernpo trrnscure hasta
que bs rios cilimlros queden en e[ mismo nivet? (g' '10m/s2¡na' 3ms)
;#
6E,UPO GALILEO
PllOBLlilIÁ ñIl{}: fl5
[Jn proyeclil <te 0.05 kg de m;is:r qrle se rntleve con tlna vek¡cir.lad de
400 rnis, penelra 0.1 rn e¡t un blot¡ue de madera fijo en el piso,
considerandc¡ consl¿r¡rte l¿l luerza des¿rceleradora. iCuál 'es la
impulsión dei choque?
Rpta: /,,, 20N,s
rBOIlLllilIA NIt0: {l{i
Una fuerza de mzrJ¡niltrd It ll)N aclúa en un plano vertical sobre un
trloque de r¡as¿r m . 5rkg. l)eturmine la veracidad (V) o falsedad (F)
de las siguientes proposici()Iies :
I) Si la pared y el bl<x¡ue en c<¡nlacto son lisos. entonces el
bloque sube con un¿r ¿rceleracitin <le r¡ródr¡b 8 mls2.
il) Si ¡1. 1É,el bkrque en reposo se mantendrh en tal posición.
III) Si p. 0,3 y p. 0.2 el bkxiue dgscenderá con aceleración
dc 0,8 m/sz.
Id,lptaz I''VV
PllOllHlllA Nlt(): ll7
El sistema moskado en la fi¡¡ura lormado por ei bloque de nrasa M I
una persona de masa m, descienden sobre la rampa lisa Si la persona
que se encu.ntr¿¡ sobre el bloque M está a punto de resbalar sobre é[,
hallar e[ coeficiente de rozarnienlo ¡t.
I,{)
Rpta:¡ ,, g./.y
l'it(lltl.lill¡l §lt(t: ll{)
ll¡rllar la tensión t¿n la cuerda que une los trkrr¡ues B C de la figura,
.: rr,, 50kg; rng,. 20kg; m6 10kg y g -l0m/s2
I,
fl,Itollllilljl ñlt(): lll
iri irrsil auk>nl1¡lico disp;ira 500 balas por minuto, cada bala liene 5
qr. cle masa y su velocklad de salida es de 600 nris' Ilallar [a fueza
mr:di¿¡ del rerlrt¡ceso del fusil mientras esta disparand
Rpta: ., , 25N
r¡ROllLti,llrl -BO: tlz
[Jna esfera cle 10 kik4rarmos cae desde una ahur¿r de li m y rlespués
<iel choque rebota hast¿r 1.25m de ¿rltitud. Calctrlar el vakrr del
irnpulso en el choque. q l.0 mls2
.¿ Rpta: / l50N.r
Pltl)Bllillil NRO: Bi|
Un carnión vacío <ie 15000 kg merrcha por una caffetera horizontal a
v, 5m/s conslante cuan<lo, de repenle, cae vertical¡nente sr¡trre el
5000 kq cle piedra. Calcul¿¡r el valor de Ia nuev¿¡ velocirlad del r:amión
con su carga.
RPta: v ,, 3.'15 m L¡
PB0I}UIIIA Nll0: ll4
Una loc<¡motora de 10000 kg de masa se dirige hacia un vagón de
4O000 kg de masa €n reposo para acoplarse a é[, a una velocidad de
0.5 rn/s. Oalcular la velocidad común después del choque'
RPta:1' 0.1 tt I s
t IOBLIIIIA §lt(l: ll{l
[Jna persona de 100 Kg. de nt¿rsa se encLlentra d<¿ntrcl de un ¿!s(]cr]slll'
que ie halta en reposo en la pzrrte superior de un eldillcio. Si el i:;rhl¿:
que sostiene al ascensor se rompe, determine la fuerza que el piso del
ascensor ejerce sot¡re la persona. cuando éste está en caída'
Rpta:N = 0
PROIll,IillA Ntt0: llfl
Un ascensor arranca hacia arriba con una aceieración constalli'e cie tal
forma que a los 10 se.r¡undos ha ¿rscendido 15 metros l)¿nlrt¡ de éi v¡
,nn pni.,rnu que lleva un obieto de 3N de peso suspendi<1o de una
cuerda. Calcular la tensión en la cuerda. g" lOmis2,
RPta:T = 3,O9N
Pn(»lI.LlIA NIIO: 9()
En Ia figura se presenta una "lxrlea kleal" que es elevada medi¿¡tlte
una fuáu constant€ tr"'800N. l)etermine la aceleración del l3kxlrN:
10m/s2 fÍ[2
$
2rn1, 50kg
Rpta:ps : 3;'4
RPta:a1 = 6 m/s2
. ,,,GJ ¡Tú Tlenes el Potencial. Nosotros la Experiencia.'.!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-93-320.jpg)
![I
§'ESXürq N
PlB0ItLlilH;t i{tt(l: f}I
Un bloc¡re dr: lj(lN rie peso es ji:lado lloi un¿'r fuerza j; , .40N a lo lerrgt>
de un;r superficie corno se rnr¡esl¡¿ en la li1¡rira. Si ¡r,. ,0.5. tl¿rllar la
acele¡ación del bloque. 1¡., J Ornfuz
f = ¡r.N
PIIO$|,ü]IÁ NIIO: 92
Rpta:a = 3,8 m/s2
I)os bloques de 130 kg <ie nt¿rsa c¿ü¿¡ uno descansan sobre superficirus
lis¿rs com<¡ rnuesfra la figura. Si los bkx¡ues paúen del reposo: carlcular
€l ti€rnpo ¡-equc¡rid«r p¿¡ra quc el trloque A se deslice 3m hacia abaio
rlei plano. g, 'l0rnls"
Rpta:t = l,4I e
Plt0lll,ll,]l1t N!l(l: flll
(-ln bbque de iJ0N es nnasir¿rdo a lo largo del plano inclinado cq:n
un¿¡ fueza F de 60 N, como se muestra en la figura. Si el coeficiente
de rozamiento cinético ¿ntre el bloque 5r el plano es 0.25. Calcular su
aceleraciixr, la velocid¿rd y posición después de 0,5 seg. de partir del
,*po.o. 5¡,.I0 m/s2.
Rpta:a= l?mls2;v= 6mls ix= l,5rr¡
Pn0BLlilIA NltO: $d
Calcular la máxim¿r acek:ración que podni tcner el coche para que cl
bto,que ro vuelque. Ijxiste suficiente rozamient¡o, de modo que el
bloque no suira rieslizamiento. ¡¡ . ' 10m/sr
Rpta:a=5m/s2
l,lt(}l¡LlIll,t iltt(t: .9 ir
iHasta qué ¿rceleracicin mírxima se le puede proporck;n;ir ¡rl c<¡che de
masa M, tal que Ia carfja de rnasa m r¡o sufra desliza¡¡tie¡rto?
g,lOm/sz ft,,0,6
Rpta:a=6m/s2
Ubícanos en Ia Av. De lo Cultura.1076 (frente a la UNSAAC)
Rpta: F- = 5O N
,YAl
I
:'i'
e.CJ-§}T§M:A {TATTLEO
!¡li0llt,¡illÁ Slt(): fXi
El sistema de bl<4ues de la figura ascien(le cr>rr ¡rceleración constante
baio la accirirr der l¿¡ fuerza F ,90N.
Si rn,' ,¡¡¡,. Zntr.',,2¡O.
liall¿ir ei valor de l¿.¡ fucr¿¿r que <rl bloque rn3 ejerce sobre m2.
l0m/sl
llp*arR=38N
flll0lll,llilIA ISII(]: t]7
[Jn¿r caia de 5 kg. Que lit:ne l;l lr¡r¡r¡a irx)strada en el ¡¡ráfico cc¡nfiene
una esfera de 10 kg¡. Si l¡¡ Íu,:lza h<¡rizontal cor) clu(? se ia[;: ler caj;r es
de 300N. D¿temrine el rnridulo de la fueza de contact<.¡ en A y Il
(desprecie las aspere2as). !¡ '' 1O mis2.
*---) F
Rpta:F^ = 25ON; §s = 250N
Pll0lllIll¡I Xll{}: fill
[¡ fueva aplicader irl bloclue A r,,aría «r¡r el tiernpo de ¿rcuert]o a kr
rclar:irin f: - 5t + 4 (F cn N y t cr) see). si p entre el tr:iso y lr:s
bloques es 0.4: determine p¿rrit r¡ué ilrsttrnle c1e tiempo e-l r¡¡rirluk.r rle
la Iuert-a de interacción enfre los bloclues ¿s tZN. Consitlere lisa la
z<¡na de contacto enlre los birx¡ues.
mA =zma*4kg g. iOrls2
Rpta:t=6,4s
PBOllLliñIAAltll: $fl
la figura.muestra un cuerpo de n¡¡rsa rn,,10kg, el cu¿rl se €ncuentra
sobre una superficie horizontal, con p(.1,0,1. Se le aplica una fuerz¿t
const¿¡nte F haciendo qu«: el cuetpo adquiera en un instant¿ dado la
velocidad de 1rn/s y un segundo después [a velocidad es de 5m/s.
l-lallar él valor de dicha fueza. <¡,.. 10m/s2.
I"](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-94-320.jpg)
![PROrlLIllIA r§ll0: I0o l'ft()llllillrl ñ-lt{},: I lll
Una cadena unifr¡rrn¿'de rnasa 10kg cuelga verticalmente. Se tira
,!rq.cia aniba con rtn¿r aceleración deSrnl*. ZCuál es la tensién en la
müacldela caden¿r? o-' 10m/s2.
(iÍTUPO G"'TLILEÜ
Un¿r c¿rdena uniforme de masa m, arelga w¿dir:¿rltnr¡rlie. S¿ tira h¿icia
ariba ct¡n cied¿r aceleración; Zcuárl es ell v¿rlor de ést¿r ¿rc,¿lotat:ión, si la
tensión en l¡r mitad tle la catiena es dos ver:es hr dc sr-r pes<.r.
Rptar*= 5g [,
f)o
1
'&
[:s una rna¡¡nit.,,l ,r.]ilu, qu€ expresa medicla d<¿ la lr¿rnsmisión de movimiento mecánico que ejerce uR cuerpo sobre otro logtando v€ncer §u
resistencia.
&:ra la existenci;r de trabarjo, neces¿tri¿rrnente clabe <rxistír movimiento mecánico y transmitido por alguna fuerza
tv,.....(Frxx?d I{r., Fd,rlso
l--d
wf -, .fd ..
lln. ,(l''cos0)d
W=0" Dtg
W,ure 0
, W efectuado por el peso cle un cuerpo en caída: W' nr¡¡h
lWl-,Nm.',Joule 1J- 107ergi<¡s
[Wl ,don I'.rgio.
pOTF:NCIA. Ls una magnitu¿ escalar que nos expresa.la rnedida de la rapidez con la cual se transfiere movimiento.
Potencia es la rapidez con la que se realiza trabajo mecánic u. P
y
t
f:n movimientorectilíneo: W ,,. t'.(t p,,y-., , !.:t-., r.,
r ,,.r t t
v Velocida<l media. I p ,Y I !- ,Woil o t/ilio
l' ,l .§
I caballo tuena (FIP)'''746 W
I caballo vapor 1CV'"735 W.
"' -t'l '-"
'Íienes el Potencial. Nosotros la Experiencia...!
§
*
¡tu
AJ? tu{.eAN{€@,](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-95-320.jpg)
![f
trs+. r-r +; '''' 'r,-fs
ACADEMIA GALILEO
m{ffigiA. t. una rnagnrtud csglar gug exp-r€§a la,,rneciir#de. ¡las"d¡ferent<¡s formas' de movimiento de la materia. Energía es la capacidad que
tiii#n los cuerpos p.ru r*lir,n un lrabajo.
E}fEnüiA CINÉTICA. (t'lc) lx aquetla lomra cle ener.tfa que liene un cuerpo, debido ¡r su vel<¡cidad. D<¡nde: llc - ll?. mv''
ENEACíA FQTENCIAL GRAVITATORIA. (F:p) l:s una magnitud escalar que n<rs expresa la posición de la partícula o un cuerpo y su
interacción con la tierra {campo gravitacional).
Ep"'mgh
@r
msü ln
I
N ivcl dc /?r?????r?*?????????
referencia
ENÉIRGÍA MECANICA. Ls la suma de la energía cinélica y la energía potencial gravifatoria.
movimiento:
Energía Elástica (Er¡).-
Brtilxj i
t[il
E_Ll4-
TEOREMA DEL TBABAJO Y IA F:NERGÍA.
1. W F.R.- LE(
2. W p.c. " --LU *" *LI:P
3. W f .r,. + W r.t¡.c. .,. LE u
I,EY DE IA CONSERVACIÓN Y TRANSFORMACIÓN DE LA ENERGíA.
Si el trabaio de la F¡ ,0, i;r energía rnecánica se conserva. En el primer teorema de trabajo y energía s¿ tiene lo siguiente
WF*=6 =+ EMo=
lNr
| .:'a .-
I
T '::
tl
I
-'K-tg0'-'//
Áreao=F*=r/zXF
Area^ = Ex= TzXKX
E* = 7., K,_*4..1r.,,¡.
Energía'lotal del M.A.S.
Lr"'/r^rf I YrKY'
Er = 7z m luf{A'z-x'z)] 't-Y2Kx2
E¡.. YzRAz -r/zKXz! + y2l<X2 -. t/zKA2
Principio de conservación de la cantidad de
Si Fq.*, - 0 , J ,., F¡ at ., ap
4p.,.0)P'''cte
F
80
Xlcm)
Pr=Pt ,
v¡'- 0
llbícanos en Ia Av. De la CalwralATí (@e a Ia ÜNSAAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-96-320.jpg)
![C!tp*
.d¿'-re- A.^demia (i.r lilco...** la ,*at $w4t GRI'PQ GALILEO
IMPULSO Y CANTIDAD DE MOVIMIENTO.
F=ma
Un¿¡ fuerza es conservativa cuando su
r,S INDEPINDIENTE DE t/ TMYECIORIA.
[]S.CERO CUANDO IA ]RAYECIORIA RECORRIDA ES CERRADA
ES COMPISI AMENTE RF,CUPEMBI.E.
Av
3m--*
tt
EHm m:;kGtrabajo cumple con las siguientes propiedades.
I.:l peso de un cuerpo, lafuer¿a normal, l¿r lueza elástica y las fuezas electromagnéticas son fuerzas conservativas.
f;¡ ftte.nade rozamiento siempre es opuesta al senti<lo del movimiento, por lo tanto el trabajo realizado por esta fueza siempre es negativo, de
tal manera que si el móvil regresa al punto <le p;rr1kia. el trabajo neto realizado sobre el seránegativo y nunca c¿a¡o. A esta clase de fuer¡a¡ ae h
c()n()ce corno lueru-as no cr¡nservalivas o disipativas.
Plt0llllj[I1r ñBO: lll
Un¿r masa de 100 gramos realiz¿r un movimir' ' circulai con una
frecuenci¿¡ <le 4l'17. Si en t , . 0 la masa está pas, 1o por e[ puáto..A
de la figura en sentido antihorario, Llallar el vak¡r del impulso que
actúa sobre la masa durante los 1/16 s iniciales.
PNOBI.UIIA NRI): 02
Un carrc¡ de masa 4M, se desplzua con una rapidez v en la dirección
del eie X positivo; en un,instante, cae un cuerpo de masa M que se
adhiere en la plataforma def ca¡ro, con velocidad V. áCuá[ es la
rapidez del sistema carro-cue.rpo.tuego del impaclo?
0'
RPta: fz' "'' 41 5V
PA0BLIIMTI NB0: 0l!
[Jna esfera de 0,4Kg <le rrasa incide en una pared
perpendicularmente y rebota luego de 0,1s. Si la fuerza media que
ejqrce la pared tiene un módulo de 70N y [a relación de rapidez antes
y después del impacto es 4/3. LCon qué rapidez. incide la esfera en
aquella pared?
Bpta: Vi,',70m I s
PItOlS,EiltA NSO: 04
Una pelota llega al techo de una habiiación y rebota, tal como indica
la figura..si el impacto dura 0.2s. ¿.Cuánto es el módulo de la fueza
resultante media sobre la pelota durante e[ impacto?
. m esf. .= 0,10 Kg.
Rpta: { = d¡¿
PI¡OBLDIIA NIIO: O5
Una granada que tiene una velocidad de 10 m/s y éstalla dividiéndose
en dos partes. La mayor cuya masa representa el 607" del total de la
granada, sigue su movimiento en Ia misma dirección p€ro con una
velocidad de 25 mls. Hallar la velocidad de la parte menor.
RPta:V2 = -12'5 m/s
PnOBLlillA NIIO: OG
En la figura se muestra un péndulo de un meko de longitud y una
masa de 0,5 Kg inicialmente en reposo. La plastilina de [a figura de
masa m' - t,5 ks y velocidad de. 4 mls choca con la masa pendular e
inicia un movimiento adosada a ella. I-lallar el valor de [a altura h a la
que se eleva el conjunto. g -. 10 m/s2
I'I¡ria, i' I)
'lr ¡
f *l ¡Tú Tienes.el Potencial Nosotros lo Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-97-320.jpg)

![k*m+*mra+"r
ffiAcademtg"
rozatnienlo)
I lallar el valor de la altura h quq ahcanz.arál
6nupo G/[LniÉo
Rpta:V * 0,3Zmls
:' -. ..
P[OIllBlIA NR(l: 27 ]: i .,
[.a resistencia del agua al deslizamiento de un bo{á es_proporcional a.
su velocidad, cuando la potencia.del motor es de.9;¡1p el t¡ote se
mueve a razónde 20 km/h. cQué,velocidad tendrá el.bote cuando el
motor entrega una potencia de 1;FIF?. :
s =. 10 m/s2 (p .. 0)
<xrnjunto (m-rM)se desplaza hasta una altura h, Calcular
de la bála en función de m, M y h.
ffnllol *l
,foo,v =#OA
PnOBLlrlIA NIt0: 2o
t{allar la potencia de un motor en l-lP, sabiendo que levaná bloq*o'
de 380 N h¿rsta una altura de 8.:m. €n dos segui.dr+s. :l
Rg{a: h =
plt0¡r[ilil/r Niror" t$
Una t¡ala de masá nr se dispara contra un bloque de masa.Mffifo se
muesh-a en la figura. Después de la colisión el centro &g:Xá¿nf
= 6,67 kmi h
Rpia;V=8,82m/s
El trab@ de la fuerza de gravedad no depende de la hayectoria
seguida, sólo de la altura ascendida o descendida.
Rpta:P:30kJ
PI0BLEMANR0:30
Un bloque de 10N de peso, asciende a velocidad constante por un
plano inclinado en 30', por acción de una fuer¿a hor2ontal F. Hattar el
trabajo realizado por F cuando e[ bloque alcanza una alturq de 10m. - ,
Rpta: Wp:lW
PIOBI,EIIA NR0: 3l
Et btoque de 2 Kg. es soltado en "A", si entre A y B se [ibera 15J.de
energía debido al roz.amiento; determine con que ¡apidez pasa el
bloque por [a posición "B".
g = 10m/s2.
r{1 _,
8Ptu:?, =bnl s
.r'
PtrOBLlllIA Nft0: 2l
Un tanque con capácidad de 2x 1d :litro§.,está.,@locado a 6 m de
altura por encima dé'una cistema. Una bomba:qué funciona durante
20 minulos htlt:e ' subir verticalmente el agua, llenando
completarnente 'el. tárque en dicho tiempo. áCuál fue la potencia
desarrollada por el motor de la bomba?
., ', . j.. ' Rpta:P =. 98 Watt
Pll0llilIMÁ NII(I: 22
[Jna grúa es capiz de lev¿rntar una masa de 100 kg a una altura de
I iin en 5s. r,Qué potencia expresada en watt suministra la maquina?
Rpta:P="3X1trW
l'lt0tll,lililA NRtl: 2ll
calcular la potencia en HP desarrollada por e[ motor'de una lancha,
sabiendo que cuando se desplaza con rapidez constante de 38 m/s
soporta una resistencia de parte del a¡¡ua de 2000 N.
Rpta:P = 108 FIP
l¡R0lll,EltlA NllO: 24
Una bomba hidráulica tiene caudal de 0,1 m3/s y debb levantar agua
hast¿¡ una altura de 15 m. Calcular la potencia que desarrolla [a
bomt¡a. (g 10 mis2)
Rirta:P -" 15 X 1G W
-.r.{{n automóvil cuya.itiasa es de 2000 kg sube por una cuesta, la
n:lqgli{Fción de esta¡§lresta es de 4m por cada 100 m de recorrido. El
dd.SffigrtJ" de ro.ámiento es igual al 8%. Calcular el tabajq que
rea1i6-d--motor del automóvil en recotrer 3 km^ú la potencia que
desanolE4=rnotor, sabiendo que este camirio fue tecorrido en 4
minutos.g= 10m/*.
V=Cte](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-99-320.jpg)

![7
lLcndxv,ris (}alileo
áx ñáa 4zM¿G
PllOllLüMA Ntt0: 44
[Jn cuerpo de 10N de peso es levantado desde el reposo a una altura
de 20m por una fueza constante de 20 N. hallar la velocidad final de
GII,Uf}O {NAI.ILEO
Pl¡(ll|illllA NIl0: 5ll
Un hc.¡mbre de 80 kg. de masa sube por un plano inclinado cle 37"
c/R a la horizontal a una velocidad de 6 km/h. Calcular la potencia
que ,lesarrolla.
Rpta: p=8O0 watt
Itf,Olll,llll¿l Nll(l: 54
Calcular el trabajo resultante realizado sobre el bloque mostrado, si
Fr = 50N
Fz = 20N
PIIOBLBIIANRO: 57
Si suelta un bloque de masa m desde el punto A de la figura. Hallar la
la masa en m/s. g= 10 m/s2
g = 10 m/s2
PIIOBLBIIA Nlt0: 4f)
Hallar la eficiencia de una máquina sabiendo
equivale a257" de la potencia útil.
,'r=P'*[oo'PF
Rpta: v=20 m/s
Pt¡0llLtIlA Nf,O¡ ¿ll¡
Un bloque de 200N de peso sube por un plano inclinado de 37
jalado por una fueza F paralela rü plano. Si el bbque se desplaza a
velociclad constante, hatlar et karbajo de F cuando el bloque sube
2Om (P.=1¡2¡.
RPtar W=4OOOJ
PnoBLllilll Ntr0: 4$
Qué potencia necesitará un móvi[, para ascender por una cuesta del
i57" d" pendiente con una velocüad canstante dtl 36 km/h, si el
peso del móvil es de 10000N y ,¿l coeficiente de fricción en la cuesta
es de2l5.
RPta: P=92OO0 watt
PttolllDllA NIIO: 47
Una persona jala un bloque de 30N de: peso mediante una cuerda
horizonial, imprimién-dole una velociclad constante de 30 m/s, siendo
e[ coeficiente de rozamientó de 2/5. C:alcutar [a potencia desarrollada
por la persona
Rpta: P=36O wat!
PIOBIDIIA NIIO: 4ll
Un bloque de 8 kg de masa se eleva r¡erticalmente desde el re6.1o
hash aLanzar la velocidad de 5 m/s 9 una altura de 10
-m
i#é
habajo mecánico se ha efectuado sobre erl bloque a[ elevarlo? W
que la
',, 2ñ
+: I
I tt:" I
,,l l
,.,.I:I
L
fl*-l
PIIOBLBIIA NIIO: 52
Al frenar un auto cuya velocidad es de 72 km/h: resbala 50 m, para
detenerse. Calcular ¡t" entre la pista y los neumáticos. g= 10 m/s2'
distancia que recorre sobre la superficie horizontal rugosa
AyBnohayfricción. (yt.: ll4, R: 10m, g = 10m/s2)
R
---"'-- - ?
r
l
rl
i
BC
d -----l
Tr:r* I
P[Oll[D,]Iil NRO: 5{l
Una bala akaviesa un poste de madera de 10 cm de espesor ingresa a
100 m/s y sale a 50 m/s. Hallar el valor de la fueza de resistencia
promedio de la madera. (masa de la bala = 0,2kS.)
Rpta:F--7500N
Rpta: v, -fiJ6 mls
Rpta: pc=0.4
i__*- 5m
¡-
v t,.,
, ,lJ.Og I ¡Tít Tienes el Potencial. Nosotros lq Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-101-320.jpg)

![r
PllOBLtrlA NIt0: 0l
[,Jn reloj ele péndulo de longitud L está inst¿rlado sobre una de las
paredes de un asensor e indica la hora correcta
"uunao
nl ascensor
está en reposo o cu¿rndo sr¡be a velocida<I constante. Si
"l
,..un"o,
sube con una aceleración <le -/
,l m/s2. ceuá moditicaci¿n det¡e
fracer,sl
sgtye el reloj para que est€ señale k hára r:<¡rrecta,?
(g¡ , 10m/s2)
PR0lll,lHA NIt{t: t)2
Un péndulo de longitud l-, se traslacla des<je la superficie terrestre a un
lugar donde la aceleración de la gravedad
".
g)r.-§i ," período se
kiplica y su bngitud aumenta en lm. lJallar et uui<;, a" I _
tJrr cuerpo en un planefa pestt li <1e r<> r¡ue pesa en ra tierra. Iraflar ra
frebuencia de un ¡:éndukr en cricho planeta si u r...u"n.iu en ra tierra
es l.
PIl{)BLIlltI¡t NB0: Oit
Pll(lllLIilIA NIt(l: t)4
¡:éndulo de longitud t_.
Rpta: A1- '- 0,77 L¡
Rnta:7, =--
T'ierrct
s, si su longitud
;'
:
Rpta: T. .- 3s
f"l
fr2
Rpta:L = 0.16 m
(Jn reloj de péndulo hecho en la tierra.es llevado a un p). ,ta X, donde
la .r¡ravedad
:r.4
,o:n: mayor que de la tierra. Despuéi rie una hoia en
ra lterTa ct relol en el planela X nrarcar¿i;
Npta, Ji6l,B0BI,DilIA Ntt0: 05
fil período de oscilaci<'rn de un pénclulo simple es
disminuye en lO"/o. Deiennine su nuevo períoclo.
Plt(lllllillil NIl0: 00
un ¡:cnrlukr de l..r¡ir r I- se hace oscilar de cros fonnas iar como se
Ty::P en Ia íigur.r. cl:n qué relación se encuenhan,rr;;;;;'"
1'2n'1'? l
r, 5
RPta:-á - -
rr6
PltOBl,lUIA NIIO: O7
En una planeta la acele-ración de la gravedad esrhdela gravedad
terrestre. C¿rlcular el valor de la relación enhe las frecunn.ias, para un
Ptl0llUillA Ntt0: OIt
Si Ia longitud de un péndulo se aumenta en u.n 2OVoáEn qué
porcentaje varíael periodo?
JJ, 1,095
Rpta:9,57o
GRUPO GALIL§O
0.4s la masa
la longitud del
PIIOBLIIffi Ntt{}: $$
En un movimiento pendular se observa qu€ cada
pendular pasa por el punto cie equilibrio. D;;;;péndulo. q',.,, 72 mlsz
}IlOl¡l,üMA Nlto:,;.ld:
fo.,.=o.Em, t'=*t
En.fu3119_debe incxenp¡lqqse-:laiongitud de un res de péndulo, que
mide':0i5, rrielros paia qüe er relo¡
';ig"
f"ñ;;;á; coneftarn€nt€
denho de.una.asc€nsor que ,rb" u.ol"riiu;;;;;;;, de 4.9 mli .
.
. ,-,:, Rpta:X = O.25 m
Plt0BHlU/t NItOr I I
El'coche se muesfa desliza con velocidad constante por un plano
inclinador:lise Calcular el período a" U. ,rr"ilu.ion"i a""t penauto
"urulongitud esde 0.5m.
Rpta:T= 1.57s.
Pn0BLllilIA Ntt0: 12
un péndulo simple de 6 m cle longitud oscira libremente en Ia
superficie terrestre, si el pénclulo
".
iLuudo ; ;r-du, el cual se
::.j:-1-{:,_",:::,,ultyru
igual al radio rerrestre. ¿En cuánto habrá que
orsmrnurr Ia longilud para qu€ el periodo no varíe?
Rpta: AL=4,5 m
Pll0llilil{A Nlt0: llt
Si la longitud de un péndulosimple aumenta en 2 m, su periodo se
hiplica. Calcular la longitucl del péndulo nn -"t *.'"'
-*
Rpta:L = O,25 m
PIll)Il[HEA NI!O: I,t
Un reloj de pénduto es [evado a un planeta en donde la aceleración de
la gravedad es de 10% me.nor.que la de la tiena-JU longitud delpéndulo es de 20cm. áCuál debe *, ;;;;;l;siiua aet péndulo
para qu€ en ese planeta funcione correctamente?
Rpta:L9=18cm
PltOll[B]IA NIIO: lt¡
Un péndulo que tiene un periodo de 1 segundo a nivel
tlevado a un planeta donde su frecuencia disminuye en
Hallar la aceleración de la gravedad de ese planeta.'- ' -
del mar es
0.2 Herb..
RPta:g=$,1'll ¡¡"2
¡Tú Tienes el potencial. Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-103-320.jpg)
![a
I
t,
I
F.I§ICA I ACADEMIA GALILEO
LEY DE LA GRAVITACION T]NIVERSAL
'lbdos los cuerpos se atraen con una fueza directamente proporcional ai producto de sus masas e inversamente pro-porcional al cuadrado de la
distancia que lars separa.
- -mMF=Li
O:.
Siendo G la c<¡nstante de la gravitación universal G=6,67X10"11Nm'z,4<g2.
Variación de ia aceleración de la gravedad con la altura.
GM
g :; para ia superficie siendo R el radio lerrestre.
"R
^ CiM para una altura h lagravedad disminuye.
5h - -l-----Ti
(R * h)''
Relacionandolasecuacionesanteriores:
*, - r_*+(R r h)'
siendo gn la intensidad gravitatoria a una altura h y g para la superficie.
.1 r::
PROilLBIIA NII(|: Ol
Si e[ raclio de Ia tierra se redujera en 507u del actual. manteniendo ü
masa el r.nismo valor. aQué.1¿alór tendríalá aceleración Lle lá gravedad
en la süperficie? g;" 10 m/s3.
RFta: E=4O¡i/s
,¡.:
PR(,IIÍBIIA ÑRO: O5
¿;;;il;;;;i;;¿' centrípeia con que
arti{i9ial de la tlá.rra,.por una órbita circular
tei.c-IülilEl radiGft ii-a;§#d sobre.iá supéfftig.
se mueve un satélite
que se encuentla a un
45
-_m/s'8
Rpta:W=15N
Rpta:h=l28OO km
La masa del planeta Júpiter es 318 veces lá'terrt';tr'.. su diárneho es
de 1 I veces mayor. iCuál será el peso en este plarr.,:;r de uir átronaufa
cuyo peso en [a tierra es de 600N? .!
PllOBLIllIlt ¿IllO: {}!}
Pll0l|[DltA Ntl(]: O4
Determiñe á"Q¡¡e;;áltura de..tar,§üperficie terrestre, la aceleración de la
gravedad.es l4.j;${ávena part¿jue el valor sobre [a superficie terreshe.
A qué alhrra sobre la superficie de la tiena,el,pé§o de un cueriio.,
disminuye en 64%
Rpr",h=l$$pɧ;;
nr¡*lfl:1n, §ob¡é.la-s,up-erfieiQ,,1g@stre el peso de una persona es 784 N. Et peso
dq{á'p¿rsén-a,,§óÜre un planeta cuya masa es iguál al de lá tierra, pero
li=F,*Fc
Jüib mdioies:¿l doble del de [a tierra, sería de
Rpta:P= 196N
a) Fueza Centúpeta. Fc[N]
Es la que da origen a Ia aceleración centrípeta de un cuerpo.
Al igual que la aceleración centrípeta, la fueza centrípeta
apuntará hacia el cenko del circulo.
V2
F =ma =m =mw2RccR
=Z F^
=: Fuerzas Radiales
Fuerza TangencialFr[N]
F,
FR
b)
o
".i$
Ubícanos en Ia Av. De la Cultura7076 (frente a la UNSAAC)](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-104-320.jpg)




![_ffi *."demia (3aW*
Una varilla de 4O cm de longitud es doblado en su punto medio
(B) formando un ángulo de 60". I{allar "x" para que el lado BC
perrnanezca en posición vertical. I-a varilla es de un material
uniforme y homo¡¡éneo.
C) 15 cm
Si el sistema mostrado se encuentra en equilibrio, hallar la
tensión en la cuerda horizontal AB, si el peso de la esfera de L0
GBU]IO §ALILE(}
A)10
D)40
m
F;-+----{
Bl20
E) s0
A) li cm
D) 18 cm
A)5N
D)20N
A) 100N;150N
D) 70N:25N
A) lrn
D) 4m
A)0.5
D)1,5
B) t0 cm
E) 20 cm
c)30
Una barra uniforme, de peso 100 N, está sujeta mediante hes
cuerdas, como s€ indica en la figura. Si una pesa 200 N, se
coloca en [a posición indicada, ¿Cuáles serán las tensiones en
N, en cada cuerda T1, T2, T3 respecüvamente?
T
3/4 L U4
A) 100;200;30Q:.
D) 150;250;350 E) 150:300; 450
C)1@;150;250
B)10N C)15N
E) Nin¡¡una
La barra tiomogénea se encuenha en equilibrio tal como se
indica, detétmiine en qué relación se encuentran [a tensión en la
cuerda horiil*iltál:,y el pesg.dii'la bana.
B)3/4
E) 1/3
: ,:::::: ¡'l.r
El-'sB ma mostado se encuentra en equilibrio, la placa
triaegl¡lar homogénea pesa 60 N. Determine la terisión en la
cuerda vertical.
Un alambre rígido homogéneo de 25 cr¡r de longitud es
doblado tal como se indica, con a : 5 cm. Para que el alambre
apoyado se mantenga en equilibrio la longitud "x" deberá ser:
Si el sistema mostrado se encuentra en equilibrio, hallar las
tensic¡nes en l¿rs cuerdas "L" y "2" . 'i.:.,i:.
.
Dl2l3 .'
cl4t3
'-,.-,,, .
il)70N;'Iti0§l
10
Determine a qué disl.ancia del apoyo articulado A se mcon'hará
la fuerza resultante de la:; cuako firerza..paddas que se
mu€shan.
B) 100N;250N
E)N.A
.]:4
' 1m '1rn '1m '1m '
B) 2m ' c¡i]rn
E) 5m
B)2.5
r:)1,0
cl2,o
*
[Jn ¡;eso "P" está colocado sobre una viga horizontal apoyada
en A y 13. l.a distancia entre los sopórtes es de 3 m y el peso
"P" estál sih¡ado de tal manera que la reacción en el soporte
"A" es el doble de [a reaccién en el soporte "t]". Sin considerar
el peso de la viga, la distancia "x" en mekos es:
10N
x---L--4p,
B) 7cm
E) 18 cm
El sistema que se muesha esÉ en equilibrio, [a barra
homogénea tiene 5 m de longitud y cada bloque pesa 5C N.
ZQué peso tiene la bana? (OA = lm)
A) 20N
D) 80N
A) 5cm
D) 15 cm
A)5N
D) 20N
B)lmN C) 60N
E)90N
C) 12 cm
B) 10N
E) 25N
c)15N
t2
¡-.
I-a vig¡a AIIC es de sección uniforme. Su peso propio es de zl0
N y se apoya en una articulación (Punb B). en el extremo C se
halla st¡metida ¿r la tensii¡n de un cable. Considerando el
sislema en equilitrrio. áCuánto valdrá la tensión del cable en N?
(considere: g -, 10 m/s2).
N y la,es!ructura es de p.,eso deEpreciabla
¡Tú Tienes el Potencial. Nosotros la Experiencia.,,!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-109-320.jpg)
![13. [.a t¡ana quebrada está en equilibrio y se pide determinar,el
valor del ángulo "a"; la barra pesada es homogénea.
14.
c) 60"
L¿r bara de la figura, de lm de longitud, es homogSánea y
descansa inicialmente «¡bre el piso y la pared vértical, ambos
lisos. E[ resort€ unido a la barra en su extrelno inferior tiene
una constante el¿rstica <]e 50 N/rn. Cuando la t¡arra está verlical
el resorte no eslá estirado. Calcular el peso de la barra si .en la
posición indicada esta se encu¿ntra en equilibrio.
A) 37"
Dl't4"
A)20N
D)50N
A)5W4
D 5W124
A)25N
D)40N
A) 1400N
D)800 N
B) 53'
E) 75"
E)30N
E)60N
B)5W8
E)4W132
B)30N
E)45N
B) 1200 N
E) 600 N
c)40N
C)35N
15. Lin la figura se muestra a una bana homogánea cle,peso "W' y
longitud "l-". Si no existé rozamiento se pide determinar la
tensión en [a cuerda horizontal. (L,.,5a).
16,
c)5w12
A partir del equilibrio existente en e[ sistsma mostrado,
determine la tensién en la cuerda perpendicular a la barra
homogénea, en su punto medio. Se sabe que la barra y el
bloque pesan 60 N cada uno.
'ttllÍtfi
17. En la figura s€ muesha un sisterna €n €quilibrio conformado
por una barua homogénea de 400 N de peso y una esfera de
700 N d€ peso, dispuesta tal como se indican. Si la bana se
apoya en su punto medio sobre la esfera, determine la reacción
del piso sobre la esfera.
c) 1000 N
Ubícanas en la Av. De la Cultara70l6 {frente a la UNSAAÚ)
18 iCuál es e,l valor db [a tensién que soporta fa cueüla horizont¿l
en el sistema en equifibrio que se muestra? l-a bana
hornogénea pesa 100 N y el bloque pesa 4{X) N.
t9.
c) 600 N
En [a fíg¡ura, el peso del t.¡loque es 15 N y ta t¡arra es de peso
despreciable. I-{allar [a reacción er-r el apoyo "C".
A) 200 N
D) 800 N
A)18j8,N
D)48;8N
A)15N
D)30tt
B) 4O0 N
E)m0 N
B)28,8 N
E) 58,8 N
B)20N
E)35N
B)1/3
E)3t4
c)38,8 N
20. En el sisteraa qu€ se muestra existe equilibrio y se sabe que la
bunu AB esrde peso despreciable, la esfera pesa 80 N y su
radio es la octava parte de la longitud du AB. éCuát es la
tens.ión en la cuerda?
21
c)25 N
Una persona de peso W camina s<¡trre una tabla homogénea,
como se mueska en la figura. áQué distancia máxima x
avaruará a partir del punto O para que la tabla continúe en
equilibrio? Peso de la barra: 3 W.
Al t_17 Bl7u24 C) 3U4
D)uA E) U3
Una placa homogénea descansa sobre dos muelles elasticos.
Encuentre k,,&r, conociéndose que los muelles están igualmente
deformados.
22
A) u2
Dl2t3
c) 1t4](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-110-320.jpg)


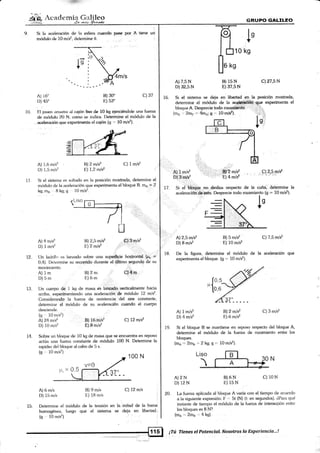

![,'t§a*,et$i*r (la
' ': ;:;::'.. t:t.:l:,i?.::':"'
'',i,'.f,()^
t'l'?ii"la fi.e¡ura se mu€ska un bloque y una cuña lisos de 8 ké y 2
r::r':!'. k¡¡, respectivamente, sobre los cuales se ejetce una fuer¿a F
constants cuyo módulo es 100 N. Determine el módulo de la
fueza qué eierce el bloque a la cuña. (g ., 10 m/s2).
GllUPO G¡ALIL=O
Si al bloque mostrado se le aplica t¡na fuena honzontal de F =
20N, hallar h fuena de rozamiento s<¡trre e[ bloque. (,u" = Q,3'
¡¿r ,,,. 0,6.W '.100 N).
35.
.*f:;JB) 20N
E)s0N
Hallar el valor de «F», si e[ bloque de 9 kg está a punto de
resbalar hacia abajo. (g ,,,. 10 m/s2)
A)10N
D)¿1oN
c)30N
36
3t) l-lallar
"tr, si <lebido a l¿r fueza «F" el cubo homogéneo está a
punto de deslizar y volcar. I)ar tancr.
A) 1l¡ N
D)25N
A p(1 -2 pl
ü pt4
A) 10% g
D) 4O% q
A)0
l)) 0,2 N
A) I
D)0,75
A)4N
D)10N
B)20N
l:) 12 N
L3) pl3
t-l (7 t 2y.¡t
B20Y" s
E) 50% s
B)2 N
F_) 0,02 N
B)0.5
E) 0,45
c)10N
C)pl(2't-tr)
c:l0,25
A) 180 N
D)50N
A}A€F
D)60"
B37"
E) 45"
c) 53"
-A
t4
<-js-1"r,,* t¡¿
ts)90N C)20N
H 80ñ
37. Hallar qué'áñgulo o0" debe fo¡mar e[ plano inclinado con [a
hbdzontal para.que,e! 'bloque esté a punió de deslizar hacia
abajo (r¿. ,= 0,75).
:t1
3?.
l.a quinta parte de Ia fuer¿a a¡jtcada a un bloque es igualra [a
tuerza de rozamiento cuyo coeficiente es 0,1 Determinar la
aceleración de bloque.
C) 307- g
[-ln cuerpo de 5 N cle peso es fransf:r,:'¡r,li> con velocidad
c-onstante por F sobre una superficie hor 'nta[. Si se quiere
triinsportarlo con una ¿¡celeracíón de 0,4 rn/s2, /en cuánto ge
<lebe incrementar a F? (g ., 10 mls2).
38, ,Hallar con qué aceleración se mueve el boque moshado
ü¿r = 0,5; m -' 10 kE; g : 10 m/sz).
c)20N
[J¡l elevador ¿isciende tal como se muestfa en la figura. Ílaüar ¡r,
parar que el bloque se mantenga en reposo]respecto al elevador.
A) 1 mis2
D) 4 m/s2
C) 3 m/s2
Un bloque se lanza con una velocidad de 20 m/s sobre un
plano horizontal áspero (irr ., 0,5). I'lallar la distancia que
reeoffe sobrc el plano hasta detenerse. (s = 10 m/s2).
B2mls2
E) 5 m/s2
B)30m
E) 6Om
B)0,150
E) 0,525
8)0,25 C)0,50
E)0,85
39.
A)2Om
,.D) 50m
C) 40m
Lln bloque parte del reposo en B y tarda 2 s en llegar al punto
A. Detenninar e[ coeficiente de rozamiento estático para las
super{icies eR contacto. (g - 10 m/s2)
40
B
34 LJn bloque de 1O N se encuenka apoyado sobre una superficie
horizontal ru¡¡osa de ¡q , , 0,5 y p,.= 0,6 Si sobre el bloque
atJri¿r una fuerza horizontal de 4 N, hallar la fueza de
rozamiento estático enl¡e el bloque y [n superficie horizontal.
E
*l I
B)6N
E)12N
c)8N
A)0,125
D)0,75
A)0,90
D)0,75
41
c 0,625
Un bloque resbala por un plano inclinado 45" con la horizontal
en un tiempo doble del que [e tomaría el resbalar sobre un
plano inclinado del mismo ángulo pero sin fricción. Determinar
e[ coeficiente de fricción.
¡Tú Tienes el Potencial.iVosotros la Experiengia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-115-320.jpg)



![ffi.+c"demía Gt*t:X
[Jn bloque estír sometido ¿r la acción de cuatro fuezas
constantes, que [o obligan a desplazarse en [ínea recta AI] "- 10
m. Encuenha rdl trabajo neto realizado sot¡re é1:
F1 ,-- 1.0 N: F, - 15 N; Fi ,, 10 N; Fj .', 20N
86
87
91.
9285
GRUPO GALILEO
[Jna {uerz¿r horiz<¡ntal. <¿n N, tie¿¡re la siguiente ley F -- 4x '+ 2.
Si la fuerza desplaza un cuerpo sobre el eje x, determine el
trabajo realizado por [a fuerza cuando el cuerpo se desplaza
desde x ,. 3 rn hasta x ,= B ¡n.
c) 140 J
lndicar lo incorrecto:
A. El trabajo se puede expresar en joule o kW - h.
B. Una {ueza variable, perpendicular a la velocidad, no
realiza habajo.
C. El trabaio de la fuerza de gravedad (peso) depende del
dcsnivel cnhe las posiciones inicial y final.
El trabai<¡ es una magnitud escalar.
El trabajo es independiente dela trayectoria recorrida.
D
E
A) 120.,
D) 150 J
A)90"
D),53'
B) 130 J
E) 160 J
c) 110 J
82. Una fuerza F clesplaza al bloqu* de 20 r§ N Sc peso a lo largo
88
clel planr, lnclinado. donde d coefrciente de fricción
".
f
5
llallar e[ lrabajo neto re¿rlizado seüre el bloqtre entre A y U (
50 N)'
r ¡lt
"
in, le
4,,'I,r' lrz r *
/'l
o.4o ¡
C¡ 420 J
A) r 50.1
r)) 200 J
A) 840 J
D)360.t
N) 52,28m|s
D) 44,76 ¡r'/e
A) Cem
D24,1
B) 100,r
E) 800 J
BJ#SJ
BSlCIJ
B)12J
E) 36J
B) 30 CV
E) 25 CV
c) 40 cv
E[ trabajo que realiza ta fugza -É de móduto constante, al
desplazar el bloque una cierta distancia, es W. Si se duplica el
ángulo " Q " realb,arla un:t¡abajo igual a 1,6 W para la misma
<iistancia.haltar"0'. . .
i.lJ:. ftf
,lHs " r-)¡ ' " ...: r.
.'ii!:í#)45
E) 37"
c)60
83
B4
Calcular la máxima velocidacl con que ur, ,trr . puede viaiar en
una pista, mbendo que el aire y la pista e.:, 'i en una resiateB4¡A
de 2 kN y que el m<¡tor tiene u¡lB potcnci¿r .re 150 hp corrl'rgtá.
efici¿ncía del 80% {Ddo: t hp =. 746 W)
B) 41,76 m/s C) 4§,66,m/s
E) ffi,¿16 nVs
F{a&ar el trabajo de F para trashdar a la cadena e-1{áft&
lsntamen:,-, &§de la peición rnstrat&arrhasb'que tádá +á
cadena se encuenhe caütre b:*r¡ps¡ficie tftl¡hontd,lisa.
ffita
I
1§0,. .,,,i§egún el trayecto moshado
..-"-¡----'
m;t",
^/
i*f
) En el kayecto "48" el trabajo del peso es
)En el trqrccto'BA" el trabqio del peso es
) El habajo neto en el trayecto "ABA"
- mgh.
.| mgh.
es cero. Podemos
C) FVF
afirmar.
A) WF
D)VFV
B} FFF
E)! /
vva wa wa
B) :* O)
345
w0 wa
t))
67
El valoi de la fuerzá F v¡uia de acuerdo a la ecuación:
F=,20-4x
x se expr€sa €n m¿ho6, F en N. Determinar el kabaio que
realiza la fuer¿a F sotlrc el bloque desde x == 2 m hosta x "= 8
m-
c)18J
lndicar la propooicién verdadera:
A. t-a fuena & rozamiento sienrpre reielba habajo negativo.
B. [¿ fucna de reacción normal nunca realiza trabajo.
C. El tr¡baio neto aiempre es positivo.
D. La potencia mecánica es una magnitud vectorial.
E. En un movirniento circular la ftreza cenkípeta no realiza
trabajo.
Un caballo jala un vagón con una fuerza F = 180 N, que forma
un ángulo de 30' con [a horizontal, con uná rapidez v -' 9
km/hr. ¿Qué kabajo hace el caballo en 1 minuto? áCuál es la
potencia qué desanolla durante ese tiempo?
r:
A) 10200J;375ri 3 W
B) 14 500 J; 225 W
c) 13 500 r5 r'zzs6 *
D) 12 5oo"/5 ¿:qzs"{iw
r:) 1i 5oo -"5 ,, ,ru ",[3 *
89. La fuerza de rgqiE*rrcia que ofrece el agua al deslizamiento de
. una ."¡6¿"5¡ffiporcional a la velocidad de la canoa. Si un
t'*á,.. motor ¿e lO{V hace marchar la canoa a 12 km/h, icuántos
ireV se nec€sitarár¡ para una velocidad de 24 km/h?
lNota 1 CV = 736 W)
A)20:CV
D) 5OCV
--€l ¡Tú Tienes el Potencial.Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-119-320.jpg)
![r
i
r'Ísrce r ACADE}IIA GALITEO
93. lndicar uerdadero (V) o falso (F):
( ) Sólo realizan trabajo las fuerzas que pueden modificar el
módulo de la velocidad.
( ) Si el trabajo total realizado sobre un cuerpo es nulo, la
fuerza resultante actuante sobre él €s c€ro.
( ) El trabajo total siempre será mayor que el habajo
realizado por cualesquiera de tas fuerzas actuantes.
C} VFF
94
95.
Desde ia parte superiot de un plano que forma 53" con la
horizontal y mide 5 m, es soltado un bloque de ? kg, tardando
2 s en llegar a la base del ptano. Hallar el trabajo realizado por
la fueza de fricción en todo el descenso (g ,= 10 m/s2).
A) VW
D} FFF
A)-11J
D) -44 J
partícula por la fueza
A)20J
D) 125 J
A) 1022 N
D) 1015 N
All;2
Dl3 2
A §l2o
D)d10
A)20N
D)45N
B) VFV
E)WF
B) -22 J C) ,s3 J
E) -55 J
B25J CI50J ,
E) Cerci '
B) 1ffo N
E) 1025N
c) 1010N
Una fuerza p ," $í + I j I N actúa sobte una partícula
conforme [a rnisma sc mueve en Ia direccién x desde el origen
hasta x = 5 m. D¿termine el trabajo efectuado sobre la
GRAVITACION 8OO9
Para que se <ié cuenta de la pequeñez de la fuerza-.de afuacción
entre dos objetos "comunes", calcule [a fuerza con la que'dos
personas se atraen (gravitacionalmente). Fara sirnplificar los
cá[cu[os, suponga que las masas de las per§üna" son In1 = trl2 =
100 kg, que la distancia entre ellas es d - 1 m y ,:onsidere que G
A) 103N B) 10'6N C) 10'eN
D) 1O6N E) 1o3N
Como los cuerpos celestes tienen masas normg§;.ila {uena
gravitacional entre ellos es muy grande (aun cuando'1a,didancia
que los separa es, también enorme). A fin de comprgbat,
anterior, calcule el valor aproximado de la tuena de ahácción
enhe la Tíerra y [a l-una, considerando que G = 10-10N. m2lkgl,
masa de la Tiena & "'. tO25 kg, mása de la Luna Mr=1d3kgy
Si en la superficie terrestre la aceleración de ta gravedad es 9.8
m/s2, determinar el valor de dicha aceleración eri un puato
situado a una altura igual a "3R/4" de la superficie tefiestre (R -
radio de la Tierra).
A) 6,85 m/s2 B 3,42 mls2 C) 3,2 mlsz
D) 4,8 m/s2 E) 1,6 m/s2
En qué relación están la gravedad de dos puntos situados uno a
una profundidad igual a la tercera parte del radio terrestre y. el
otro a una altura doble del radio terrestre, ambos respecto de.la
superficie de la Tiena.
La masa de la Luna es 1/80 de la masa de la Tierra y su radio
1/4 de ésta. áCuá es la aceleración de la gravedad en la
superficie de la Luna? (g .', gravedad en la superficie terrestre)
Be;2
E)6;1
B) cl$
E) s/16
B)40N
E)80N
C)1;3
C)s/5
c) 180 N
6. Un cuerpo pesa en la Tierra 180 N. Determíne Lqué peso tiene
en un planeta cuya masa es el doble de la terrestre y cuyo radio
es el hiple del radio de la Tierra?
llbícanos en la Av. De la Cultura7016 (frente a la UNSAAC)
A)@'!+n C) trMtt-
1j ron
áCuál ee la aeeleración de la graveclad en la rupedkie del Sol
culp'radio equivale a 100 radios tene¡trm y cuya dcnsidd
media es 1/4 de ta densidad terreske?
C) 2¡15 rr/f
Si consideramos que la separación enhe la Tierra y la l-una es
"d" y que además la masa de la Tieffa es igual a 81 vecps la
masa de la Luna, decir en qué lugar del e+mio enhe estos dos
cuerpos se puede colcrar una pequeña masa para que se
encuentre en equilibrio. Dar respuesta eomo la distancia de
aquel punto a la Luna.
A)0,9 d
D)0,2 d
c)0,1 d
Dos cuerpos se atraen con una htena de 800 N. §i uno de ellos
duplica su masa y el oko la triplica y h distancia entrg ellqs s€
cuadriplica, ¿cuál es la nueva fuerza de atracción entre ello§?
A) 125 mls2
D) 300 m/s2
A) 100 N
D) 4OO N
^, 5Ffr,
-ll
ul'o.4
A) 3F
DJff
A) R
1+K
D) 3
K
B) 375 m/s2
E) 250 m/s2
B) 0.6 d
tr) 0,5 d
B) 20O N
E) 600 N
B) !{
ll
-, 5^F'
r.,
-4
c)30oN
c¡ I l¡;'
4
C) KR
K*l
10. Determinar la fueza resultante que actúa sobre la masa "m"
(im2
Considere: ,h'-'.-)
a'
C' - O"'.á."'O3mo2m*m
§¡:id$§:cueryos de masa "m" cada unb, mparados por una
distarrcia llL" se atraen con una fueza "F", halla¡ la fuerza
resultante que soporta la masa "rn" del sistema mostrado.
o
't
l , ¡L
s*fl @u*
c)5F
t2- Un planeta de masa "M" tiene un satélite de masa "m" que gira
circulantemente al¡ededor del planeta, en una órbita de radio
'R". ¿A qué distancia del planeta entre m y M, la aeeleracién de
la gravedad es cero? (M : l€m)
13. Sabiendo que un satélite gira alrededor de su órbita y ademas sc
halla a una altura "h" sobre la superficie terrestre, donde la
aceleración de la gravedad es la 16u parte de la gravedad
terreshe. Calcular con qué velocidad gira e[ satélite alrededor de
su órbita.
L
B 2F
E) 8F
B) r]?
l+K
,) i_a
I +"Kl
B) GMt
2R
GMt
/t](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-120-320.jpg)
![./¿:á rcacl emía Gallleo_
i*. y'a ,4^_ qaad¿e
i4. Dos satélites de ¡nasas Mr y Mz giran alrededor dc un flmeüa, en
órbitas circulares de radi<¡s R1 y R2 respectivarn€nte. §i el pariodo
'del
satélile M, es de 120 días, hallar e[ periodo del satélite M2.
(R2 ,.4R1).
A) 960 días
D) 480 días
C) 680 dras
15. Un planeta "M" üene 2 satélites, "A" y "B", los que giran a su
alrededor, describiendo órbitas aproximadamente circulares. Si
el periodo de "8" es 160 días y el radio de la éóita de giro de
"A" es la cuarta parte del radio de la órbita de "8", hallar el
periodo de "4".
A) 10 días
D) 21¡ días
C) 20 días
16. I)os satélites de l;i
-l'ierra,
cada una de m¿xa "m", se mueven en
í¡rbitas circulares concénhicas con la Tierra. Si sus posiciones son
2R y 4R respecto del centro terrestre, en qué relación están sus
energías cinéticas.
A)1/6
D 114
17. En el sistema planetario moskado, el planeta demora 6 meses en
ir del apogeo al punto "P" y, al perigeo, 15 meses. Si el área
toial de [a elipse es "S" hallar el área sombreada.
B) 720 días
E)240 días
B) 15 días
Il) 30 días
B) 1.125
E)4
B)S/3
EStz
Bl27 7t lSG], C) 18 7t l8c't2
E81,n l8G'12
ot:[i-Yn
2
EI Ji V,,
6ürfo nfil,l¡.Io
Imagine que la masa del Sol se volviese repentinamentc ¡1 vcr
más grande. Para que la fuerza de atracción del Sol sobre la
Tierra no sufriese alteraciones, la distancia entre la Tierra y el Sol
tendría que volverse:
A) 4 Veces mayor
B) 4 Veces menor
C) 2 Veces mayor
D) 2 Veces menor
E) 8 Veces mayor
Sea "F" la fuerza de atracción del Sol sobre un planeta. Si la
masa del Sol se volviese 3 veces más grande, la del planeta, 5
veces mayor, y la distancia entre ellos se redujera a la mitad, la
fueza de ahacción entre el Sol y el planeta sería:
22.
23
¡ ,,- c) 7,5F
:: ' .'.i
Un satélite es colocado en órbita a 36"Q00 lcn t{¿ altura (misma
aftura del intelsat), de modágue el ptano de #.brbita pña por
los polos de la Tierra. Un cik*q:.¡ador situado¿ñ el poür sur, ve
pasar el satélite sobre su cabqi*i**n§ !¡ **trna¡iana dc un dla
determinado. h pf@m
observador será' ,:, :,:,
pue sobrc este
A) 3F
D)(15/4)r
gravitatoria en Júpiter?
A) L50 veces menor
C) 500 veces menor
E) 500 veces mayor
A16W25
D) 4W9
la superficie.
G = constante de gravitación
^
EM B)
1l n
D) PM-
!¡n
B) 300 veces mayor
D) 300 veces menor
c)3R/e
B) 15F
E) 60F
B)N4
EW2
A)S/4
D)S/5
A) a las 12 h éel misrr:*r día
B) a las 20 hdel misño día ,,1
C) a tas 24 h det mlsmo día
D) a tas 8 h del da siguiente
E) a las l2 h di e siguientÉ
Z+. Eiqji§¿" Júpiter'es casi ,l.0 veces mayor que el de la Tiena. Si
,u rn¿¡¿-S¡$cho planeta exte¡ior (o sea, de los que están fuera
. del a ¿mi¡ai4@) fuera igual a la de la Tierra, icuántas r¡eces
:: rn€oor que'€ii:r';sta seía la aceleración de la gmvedad en
':.': Júpiter? ,::l
' : . .A)..!00 veqeímenor
BJ'56v9ces menor
C) 50 veces mayor
D) 100 veces mayor
El 150 veces menor
25.. l-a masa de Júpiter es casi 300 veces mayor que la de la Tiena.
' Si el radio de aquel planeta fuera igual al radio terreshe,
ácuántas veces mayor que en la Tierra. sería la aceleración
26. Un cuerpo de masa "m" se abandona des& una altura igual al
radio de la Tierra (h-R), respecto de la superficie tenestre de
masa "M". Hallar [a velocidad del cuerpo "m" cuando choca con
universal
tlcMt_
!n
Fm
!R
E)
27. Un cuerpo pesa al nivel del mar 75 N. ¿A qué altura debe
elevarse para que su nuevo peso sea 3 N?
R radio terreske
A) R B)zR C)3R
D)4R E) 5R
28. En un punto situado a una altura "a" de la superficie terreshe, la
aceleración de la gravedad tiene magnitud "gi" y a una
profundidad "a" de la superficie terreshe tiene magnitud "g2".
Hallar: "a", si: 8gr=Qg, (R '- radio de la Tiena y suponer que la
Tierra es esférica, maciza y homogénea).
18. I:n la figura se oi¡serua el movimiento de u' ¡ri, ,,eta'gn,tor.no a
una estrella "I:". Si se sabe que desde [a F'.,i.rón "P" tardael
quíntuple en llegar a "A" que de "C" hasta )", encontrar quá
fracción de la superficie elíptica es la porción sombreada.
A) 1/6 Bl2l3
D 3t2 E) N. A
cl,4t5
(lalcular Ia densidad de un planeta de forma esférica, si un
satélite gira a su alrededor en una órbita circular con periodo "T"
y a una distaneia de la superficie del planeta igual a la mitad de
su r¿ulio "R- (G = cle. universal de gravitación).
19
Un cuerpo de masa "m" es lanzado verticalmente hacia arriba
con una velocidad "V6". Desde [a superficie de la Tiena, donde
su rnasa es "M" y su radio "R". Calcular su velocidad, cuando ha
recorrido una altura igual a "R".
(,, rcr
['.,{o.,l
A it lt tqc't"
D 9 7t lzc't'
A)v"
2
r» !!-Yn
4
y^
c)
-4
GM
2R
f;ril ¡Tú Tienes el Potencial. Nosotros la Experiencia...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-121-320.jpg)

![-
#'e- n.aclerni4 Catlleo
;-¡¿** .!,<. ,r.it $ua4t
^.
d=Zm
(,¡ "
m,
B)2mN
E) 4O0N
GRUFO GALTLEO
c) 100 N
4:t. ¿A qué altura sobre la superficie de la Tierra el peso de un
cuerpo se reduce a I r novena parte de su valor en la superficie?
Il -¡ r¿rdio de la'lierra
A) 3R
DI wS
En el gráfico, detenninar la magnitud de [a fuer¿a de inbracclbn
enhe las dos esferas. Mr ,, 10 kg, m, '= 4¡ ¡n.
tr ?,
G - 6.67.10-" 1vÍ-, -,-
Kg
50
B) 2R
r) 9R
c)Rt2
44. Dos satálites "A" y "t1", de ig¡al m¿lsa, se encuentran a
diferenüer dlstanci¡ls lla I Rs rcspeeto ¿rl centro de la tie.rra. §i d
satélite "A" elemora el dohle del tiempo que demora "B'" en dar
una vuelta completa alredetlor de la Tierra, la relación R/Rs es:
€
m?
A) 2§N
D)lmN
A) 30
D)120
51. Dos cuerps sxpÉrincentan una
igud a 16 f*. §i *t r€lwión
rna€&iñ&d & &a m¡sva fuer¿d
A)l Ble
D {laD) iñ
45:. LJn cuerpo pes¿r en la strperficie terrestre 16 N. ¿A qué altura
sobre la superlicie lerrestre e[ mismo cuerpo pesará 4 N? R "=
c)4
46. Dos planetas A y B giran alrededor de una eskella. El planeta A
demora en dar I vuelta 365 días y et planeta B demora 292O
días. áCuál es la relación (Bo/Ru), siendo R¡ y Rs los radios de
I es el período del movimiento olrcular uniforme de radio "r" de
.un planeta álrededor del Sol de. masa M, y G es la constante de
-.gmvitación univétsat,-La.dliaiion que vincula al periodo de un
ilan¿,ta con su velotki'ad "ü' es:
radio terrestre
A) W2
D)3R
sus órbitas?
A)4 B)u
D 1lü1 1,) 1/4
Lo correcto es:
A) Solo I
D) Solo tll
A) 4 mese.s
I)) 6 meses
A) Solo I
D)l y III
¡t TL=9¡' G14
ct T2 =4nTc',.M','vo
:l
Áa 4nlGM
El I' =
-_:--
'vr
ñ) rzGM
B),1 -=
Dt Tz =Lut' GrM,
B)28/3
F) 3R2
cl64
47. tJn satélite de [a 'l'iena se encuentra en un;¡ ó¡bita eübtica,, tal
como se muestra, luego de afirmar :' ,,r,'
A
T-a energía cinética en A es ma@r que
"r't9.:
, :':i;r::'
l,a energía potencial en A es maydr que3n f,-""'i':
La energía total en A es mayor que en B.
Alrededor de un planeta M giran 2 satélites de masas, Mr y Mz
con mdios Rr y &; tal que Rr=dfi1. Calcule el per{odo de }12
siendo el de Mr, 30 dlas (en días).
I.
il.
til
B) Solo II
L) Il y lll
B)lvll
ll) I, II y III
48. I.a fig¡ura mueska la érbita de'un planetl+'álrededor del Sol; si
para ir desde (A) hacia (B) demora 4 meses, aqué üempo emplea
--t
para el recorrido BC'?
--"--,(D)
B) 60
El2ñ
CHoQUES E IMPUI§O
Una esferita de 1 kg se desliza sobre una superfkie hofrpnbl
con una velocidad f = tO,gl m/s, irrcidiendo sofure una paled
vertical con un ángulo de incidencia de 37". Si luego del impacto
que duró 0,1 s pierde el 25% de su rapidez inicial y además su
velocidad de rebote es perpendicular a zu vetocidad inicial, équé
fuerza media aplica la pared vertical a la ederita?49. Respecto al movimiento planetario, indique cuál (es) de las
proposiciones es (son) conecta(s):
l. Describen kayectorias elípticas, dondi en uno de
los focos se encuenha el So[.
il. El vector posición del planeta, respecto al So[,
' barre áreas iguales en intervalos de tiempos
iguales'
m. El periodo de traslación del planeta, alrededor
del §ol, es proporciona[ al cubo de su radio
vector medio.
-a á ¡
#¡l+1-6]itcr
'. ü:Ít- --'i . x+,i ¡-^ .
-'- - ¿:'-- f ¡:')
(A)
B) 2 meses C) I meses
E) 12 meses
A) 100 N
D)30O N
B) 125N C,zooN
E) 500N
Una raqueta logra golpear una pelob de @nis de 200 g,
desviando su dirección según como se indica' Si v1 = 35 m/s y vz
= 75 m/s, iqué fuerza media ergerimenló la pelota' si la
duración del contacto fue 0,05()?
C) Solo II
: | :t lll lllll | ! qE-l ¡TúTieneselPotencial.NosotoslaDxperiencla...!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-123-320.jpg)


![¡r=
§'.ISICA T ACADE§tr}A GJULTL§Ü
24 . LQué m¿rs¿r <le conrbuslible es nect?s¿lrir¡ r)rroj¿tr con vclocidari 3v
resJ)ed() ¿ll il()hcl.a de nr¿ls¿l M para <¡trru l;r velocitl;rd <le esle
¿rulnentedeva 1.1v'?
A) M/20
D)Mlll)
13) Mi2{;
I:) W1(ú
c)Mi:l(i
2{¡. Sobre un t¡ote de 10 kg en reposo y en a{Juas lranquilas, hay dos
personas paradas en slrs extremos. A es de 4.0 kg y f3 de 50 kg.
Si A y t3 comienzan a camin¿¡r para enconharse con velocldades
de- 2 n'tls y 4 rr/s. respectivamente, respecto al t¡<¡te. Determinar
la velocidad del t¡ote cuando A y B se encuenlran. (No considere
fricción entre el bote y e[ agua)
A. 2,{l mis hacia [a izquierda
B. 0.2 m/s hacia la izquierda
C. I,2 m/s hacia la derecha
D. 1.2 m/s hacia la izquierda
E. 0,6 m/s hacia la derecha
El sistema mosk¿¡do está carente de rozamiento y se le abandona
en la posición moshada, determine la distancia horizontal que
habrá reconido la plataforma cuando la barra homogénea se
coloque en posición horizontal. (R ,,., 0,8 m).
4
&,-.§r-H
ll -¡/§
é
É
26.
F
f.-
C) 6cm
27 . Las dos t¡alas se incrustan simultáneamente en e[ bloque. áHasta
qué altura se elevarár el coniunto? Se sabe además que v=8 m/s
y g 10m/s2.
nlv.€t=+--
€-: -
|.nV
A) Ocm
D) 8 crn
A) 0.1 m
r)) 0,4 m
A)0,4
D)0.7
B)2. cm
f'-) 10 cm
B) 0,2 m
E-) 0,5 m
28,
c) 0,3 m
fija y ta Íuena de
de a<uerdo con la
restitución entre el
Un cuerpo choca contra una superficie
contacto entre ellos varía en el liempo
siguiente. gráfica. I{allar el coeficiente de
cuerpo y la pared, si: 4Ai , - 5A2-
F(N
t(s)
il)0,1, C)0,6
E)0,¡l
29. Sobre una rqesa lisa se lanza una esfera de masa m, la cual
colisiona frontal y elásticamente con otra esfera de ñásá rrr2,
inicialmente en reposo. Si después del choque arnb¿rs esferas se
Ilbícanos en la Av. Dé ta Cittara7076 {frenie a la UWSAIq
i;**
rnueven con la rnisma rarpirir:z
hall¿rr l¿r rci¿rciírn (rr2,il1).
pero en dirccci<rnes opuerslas.
c) 1i?.A) r
D) 1{3
fi) 2.!¡
:-t( ) Una persona del rn¿rs¿r rn está en reposo en e[ exlrelno tle un¿¡
tabla de m;xa m/ll y longiLud I-. Si camina hasta el oko extremo,
iqué distancia retrocede l¿r tabla sotrre el terreno horir.ontal liso?
AIU4
D)rJ3
A vlL9 e vl20
D) vl12 y vll3
A) VW
D) FFV
A) 1 m/s
D) 4 m/s
A) 1 m/s B) 0, 6 mis
D) 0, 4 rn/s E) 0, 8 m/s
A)6,3
D)9
B) vl2o y vl27 C) vl y vll
E vl20 y vl20
B) VFV
E) VFF
B) 2 mis
E) 5 m/s
C) 0, 2 m/s
B) 8,3 C)8
l:) 9,6
8 4t_t3
ElUs
cl3u4
21 t-Jn hombre de masa m, que s€ encu€ntra en reposo en una
lancha de masa 4.m, lanza un paquete de masa m/4 con una
rapidez horizontal "v" hacia otro hombre de igual masa, que se
encuenha en reposo en otra lancha idéntica a la ante¡ior.
Calcular las velocidades finales de los dos hombres.
32. A partir de las siguientes proposiciones, indiqu€ cuál es
verdadera (V) a falsa (F):
I. Si se hiplica la velocidad de una partícula, su cantidad
de movimienlo también se triplica.
[. Si un cuerpo se desliza por un plano inclinado liso, su
cantidad de movimiento perrnanece constante.
U. Dos pelotitas ion la misma masa y la misma rapidez
poseen la ¡nisma cantidad de movimiento.
33
34
C)FW
Un cuerpo de 4 kg se desliza sobre una superficie horizontal lisa
con una rapidez de 3 rnis. Si en el camino le cae verticalmente
un'bloque de 2 kg, quedándose adherido al cuerpo, hallar la
rapidez final del sistema.
C) 3 m/s
En él puerto un hombre de 100 kg decide caminar hacia delante
a razón de 2 m/s sobre un bote de 1000 kg. Hallar la rapidez que
adquiere el bote.
Desprecie todo tipo <ie rozamiento.
35. Una pelofa de béisbol de 200 g llega al t¡ateador con una rapidez
de 1li m/s, es qolpeada por el bateador y sale en direccií¡n
opuesta con un¿] rapidez de 25 m/s. ¿Cuál es el módulo del
cambk¡ de la c¿¡ntid¿rd cle movimiento (en Ns)?.
36 Pedrito, cuya masa es de 60 kg. el cua[ flota en reposo sobre el
agua. Si Peclrito camina hacia el otro extremo del tablón y cae al](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-126-320.jpg)
![r-4 {f,.
.)i
1l¡L.s
'lt
¡,. .
¿¡fJuii Con un¿t velocidad ht:rizr>nlal de fl ¡n¡s. ralle la rapidez del
tat¡ki¡t en esr¿ inst¿rnt¿ (err rnis).nt ,.,,,,,., l {)0 ke.
GR.UPO GALILEO
en dire(:(:ión opuesld. I.[aliar la fuerza nredia del qolpe. si ltr
pelottr penlanece en ü)ntack) con ¿l bate 2 milisegunclos,
R)2 KN c) 3.5 kN
45. Si el sislema moslrado se suelta cies<le el reposo estanr.ro el
resorte (K ,,' 100 Nlm) comprimidol< ,, jj m, halle [a máxima
rapidez que adquiere el bloque {9 masa I kg. (mn -. 2ms = i kg)
,'t i::lck"ix ia {., ; I i iici:J<. ¡r,:, 6taq4¿
¡1) 1,.1i c) 4,8A) :1.()
r)) 7.3
It7. Si la pelota rnostrada en el gráfico sok; invierte su movimiento
ln¿rnterriendo su ra1:idez. halle el irnpulso i¡ue recibe por par.te de
la pared. (rn ,,-¡,,,"
. 0,1 kg)
A) 2íN.s
l)) 4 i N.s
f3) -2iN.sC)3iN.s
l,:) 20 i N.s
A) 10 m/s
D) 15 m/.s
B) 20 m/s
E) 25 mis
B) i35 m/s
E) 50 mis
B)27N
11) 32 N
It) 1200 m,'s
E) 1300 m/s
C) 5 m/s
C) 4.Lr rn
(l) :ir I
(l) 1500 mrs
C) 3cm
Í18. (.lna partícula A de masa m y velocidad 2i mls var al encuentro
de. una partícula B de mas¿l 2 i m y en repbso. Si después de la
colisirin enhe A y 13, B adquiere la vek¡cidad i ¡n/s. halle la
velocidad de A (en mls)
A)0
D -2i
ll9. Un bloque de 500 g posee la rapidez most¡ada cuando de pronto
enrpie.zit ¿r acelerar con 3 m/s2. l)etermine su mr¡rnentum lineal
cuando transcurta 3 s ¿r partir del instante mostrado.
4ó. Una voleibolista hace un saque-mate, imprimiendo a la pelota
una velor:idad que la eleva verticalmente hasta 7,S m de altura y
cuando está reJ¡redando le da el golpe a 2,5 m de altura,
lanzand<¡ la pelota con una velocidad horizontal de 30 m/s, hallar
la tuena promedio que le imprime si el tiempo que dura la
acción (qolpe) es 0,02 s.
(Masa de la pelota 0.4 kg)
I^
A)200,J N
io8oH/3 N
C)
A) I 2 kg m/s tl) - li kg¡ . m/s
I)) i 5 k5¡ m/sl:) i 7kg .rn/s
C) -Tkg mis
40 Se muestra ¿r un¿r person¿l que al saltar sobre el carro queda en
reposo. l,Cuál es l;.¡ vekrcidad dei carr<> luego de esta r¡»eración?
l, D)aoofi,N' r¡zoo"v,'T0 N
47. 'Uá buerpo de 10 kg de masa que se mueve sobre el eje x, es
afectado por una fuea¿r variable en módulo pero de clirección
horiz-ontal constante. cuya gráfica en <iependencia con el tiempo
se muestrá. Si en t = 0.s la'rapidez rie) cuerpo es 5 mls, halle su
' rapide.zent=7s.
4i IJn hombr<¿ r:ie tnas¿r l¡l va corriend<l con un¿] mpidez de I n-r/s y
da ¿rlcan<p ¿r ll)i ;!ul()ln¿)vil <ie m¿rsa 4 m que marcha a "azón de
li rl/s y se sutx¿ a é1. aQue velor:rdad adquirirán ambos si la
c¿lrret¿l se rrlrx¡í¿r en la misma dircr:r;irin orre ei hombre?
C) ?- mls
'l,J rti.:
l)1f,.:r.
Bl l:l rr . C) 5 m,'s
(,lrr ¿rvrrirr rlite vuela:r horiz<ln1¿llmente en el inst¿rn1e m«¡sirad<r
J)reser)Iil un¿t mas¿) M (incluido combustible) y una rapidez v. Si
clr c¿se instante expulsa lroriz<lnl¿rimente cieÍa cantidad de
corribrrstibie con una velocicl¡xJ í3 v respecto del ¿lvión. determine
l¿r ura-.¿r del combustibie exl.ruisardo. si lzr ri4:idez del avión
r¡llil¡(,¡1lO err tl.l V.
48. Un fusil automático dispara 1200 balas por minuto. Si irt ¡iÉi-(.)
de cada bala es de 2 5¡ y su rapidez es de 800 rn,s. h¡ilar i:r ,.,ajr:r
cle ia acción media del retroceso del fusil
A) l'r rtr s
I )) 1 nr,'s
A) Mi:10
r))Mi40
A) 0. ltn
l)) U.4 m
B) 4 mls
Ir-) ll rnr's
13) Milr i
Í:.M142
t3) 0.2 m
t) 0,5 rn
A) 30 mr's
D) 45 m/s
A) 16N
r)) 20 N
A) 1000 rn/s
D) 1400 m/s
A) 1cm
D) 4cm
t/
49. Si el proyectil de i00 g se incrusta en el bloque <ie 21.9 kt; se
observó que [a máxima defr¡rmación en el resorte fue 10 crn.
Determine la rapidez v del gráfico mostmdo.
' Llsil
4ll. []n cañ<in de 1200 kg¡ disparar una bala de 20 kg con una
r¡ek.:cidad de í{10 i nr/s; se1¡ún muestra la figura. Determinar la
rnárxima cornpresir'>n del resorte.
50. La fi.r¡ura muestra una esfera de 1 kg que desliza desde el punto
A por una superficie lisa. Cuando la esfera impacta en e[ péndulo
queda adherida. áCuánto se loqra elevar el conjunto esfera-
péndulo luego del imp;rcto?
i,j.9 {§
13) 2 cm
E) 5cm
cr) 0,3 m
[jn:r pelotar de l¡éisbol tiene un¿] rnasa de 150 g. si es lanzada a
24 rnis y des¡rués tle h¿rber sido trateada su rapidez es de 36 m/s
i¡l
¡.Tú. Tienes 9l Potencial; Nosoúros la Experiencia..,!](https://image.slidesharecdn.com/fsicagalileo-150429210938-conversion-gate01/85/Fisica-galileo-127-320.jpg)