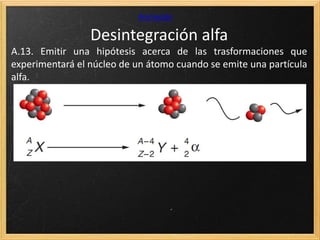
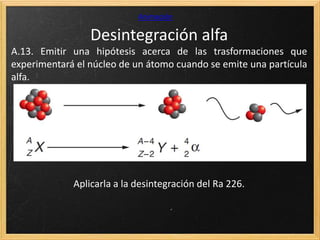
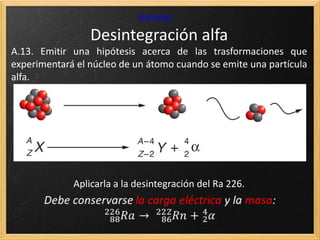
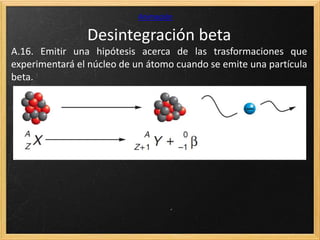
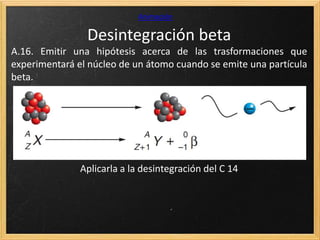
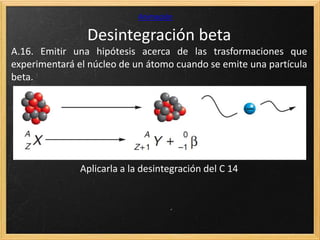
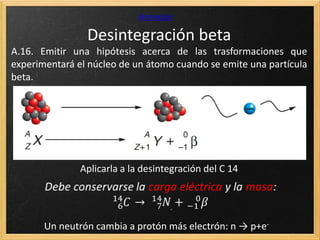
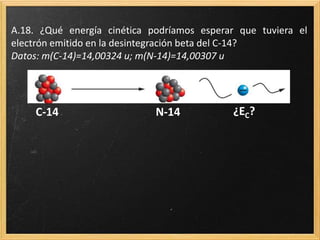
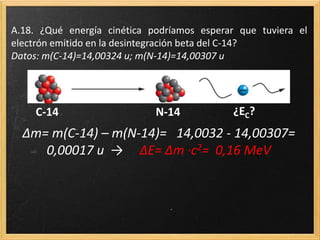
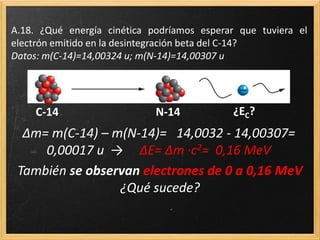
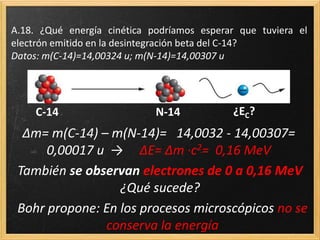
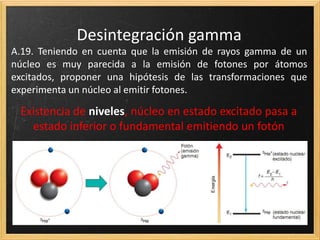
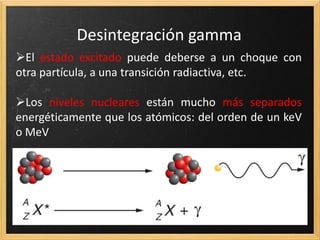
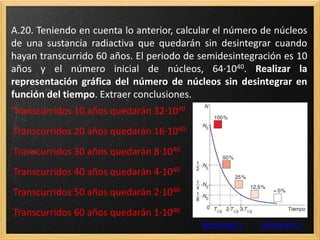
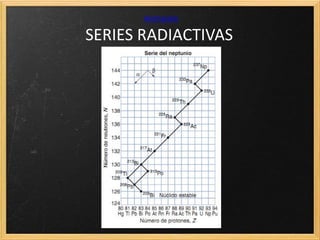
El documento trata sobre la radiactividad y la desintegración de núcleos atómicos. Explica que existen diferentes tipos de desintegración como la alfa, beta y gamma, y cómo afectan estas al núcleo original. También describe las series radiactivas y cómo ciertos isótopos se desintegran en otros de forma secuencial, llegando eventualmente a uno estable. Además, presenta deducciones sobre la ley de desintegración radiactiva y la relación entre el periodo de semidesintegración y la constante radiactiva.

1. 13.3 RADIACTIVIDAD
¿Cómo se desintegran los núcleos?
Física

2. Desintegración alfa
Animación
A.13. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
alfa.

3. Desintegración alfa
Animación
A.13. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
alfa.

4. Desintegración alfa
Animación
A.13. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
alfa.
Aplicarla a la desintegración del Ra 226.

5. Desintegración alfa
Animación
A.13. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
alfa.
Aplicarla a la desintegración del Ra 226.

6. A.14. ¿Qué relación debe existir entre la masa del núcleo padre y la
de las partículas resultantes para que se produzca la desintegración?
En conexión con esto, ¿por qué los núcleos emiten partículas alfa y
no cuatro nucleones?

7. A.14. ¿Qué relación debe existir entre la masa del núcleo padre y la
de las partículas resultantes para que se produzca la desintegración?
En conexión con esto, ¿por qué los núcleos emiten partículas alfa y
no cuatro nucleones?
 Masa del núcleo padre mayor que la suma de las masas del
núcleo hijo más la partícula alfa.
 La diferencia de masas aparece en forma de Ec que
transporta principalmente la partícula alfa.
 Partícula alfa muy firmemente ligada y su masa es mucho
menor que la de los cuatro nucleones.

8. A.15. Calcular la energía cinética de la partícula alfa emitida cuando
se desintegra el U 232 (232,0372 u) en Th 228 (220,0287 u).

9. Desintegración beta
Animación
A.16. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta.

10. Desintegración beta
Animación
A.16. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta.

11. Desintegración beta
Animación
A.16. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta.
Aplicarla a la desintegración del C 14

12. Desintegración beta
Animación
A.16. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta.
Aplicarla a la desintegración del C 14

13. Desintegración beta
Animación
A.16. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta.
Aplicarla a la desintegración del C 14
Un neutrón cambia a protón más electrón: n → p+e-

14. Desintegración beta +
Animación
A.17. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta + (positrón, electrón con carga negativa).

15. Desintegración beta +
Animación
A.17. Emitir una hipótesis acerca de las trasformaciones que
experimentará el núcleo de un átomo cuando se emite una partícula
beta + (positrón, electrón con carga negativa).

16. A.18. ¿Qué energía cinética podríamos esperar que tuviera el
electrón emitido en la desintegración beta del C-14?
Datos: m(C-14)=14,00324 u; m(N-14)=14,00307 u
C-14 N-14 ¿EC?

17. A.18. ¿Qué energía cinética podríamos esperar que tuviera el
electrón emitido en la desintegración beta del C-14?
Datos: m(C-14)=14,00324 u; m(N-14)=14,00307 u
Δm= m(C-14) – m(N-14)= 14,0032 - 14,00307=
0,00017 u → ΔE= Δm ·c2= 0,16 MeV
C-14 N-14 ¿EC?

18. A.18. ¿Qué energía cinética podríamos esperar que tuviera el
electrón emitido en la desintegración beta del C-14?
Datos: m(C-14)=14,00324 u; m(N-14)=14,00307 u
Δm= m(C-14) – m(N-14)= 14,0032 - 14,00307=
0,00017 u → ΔE= Δm ·c2= 0,16 MeV
C-14 N-14 ¿EC?
También se observan electrones de 0 a 0,16 MeV
¿Qué sucede?

19. A.18. ¿Qué energía cinética podríamos esperar que tuviera el
electrón emitido en la desintegración beta del C-14?
Datos: m(C-14)=14,00324 u; m(N-14)=14,00307 u
Δm= m(C-14) – m(N-14)= 14,0032 - 14,00307=
0,00017 u → ΔE= Δm ·c2= 0,16 MeV
C-14 N-14 ¿EC?
También se observan electrones de 0 a 0,16 MeV
¿Qué sucede?
Bohr propone: En los procesos microscópicos no se
conserva la energía

20. 1930, PAULI: Existencia del Neutrino
 Muy difícil de detectar
 Explica la inestabilidad
del neutrón mediante la
interacción débil
 Lo que realmente sucede
en la desintegración
beta:
n → p + e- +

21. La cuarta fuerza fundamental de este curso:
La interacción débil

22. Desintegración gamma
A.19. Teniendo en cuenta que la emisión de rayos gamma de un
núcleo es muy parecida a la emisión de fotones por átomos
excitados, proponer una hipótesis de las transformaciones que
experimenta un núcleo al emitir fotones.

23. Desintegración gamma
A.19. Teniendo en cuenta que la emisión de rayos gamma de un
núcleo es muy parecida a la emisión de fotones por átomos
excitados, proponer una hipótesis de las transformaciones que
experimenta un núcleo al emitir fotones.
Existencia de niveles, núcleo en estado excitado pasa a
estado inferior o fundamental emitiendo un fotón

24. Desintegración gamma
El estado excitado puede deberse a un choque con
otra partícula, a una transición radiactiva, etc.
Los niveles nucleares están mucho más separados
energéticamente que los atómicos: del orden de un keV
o MeV

25. SERIES RADIACTIVAS
Primarios
Los núcleos pueden clasificarse en
Formación de la Tierra,
vida media muy larga,
U-238, Th-232, U-235

26. SERIES RADIACTIVAS
Primarios Secundarios
Los núcleos pueden clasificarse en
Formación de la Tierra,
vida media muy larga,
U-238, Th-232, U-235
Edad menor que la
Tierra, vida media más
corta, provienen
desintegración
primarios.

27. SERIES RADIACTIVAS
Primarios Secundarios Inducidos
Los núcleos pueden clasificarse en
Formación de la Tierra,
vida media muy larga,
U-238, Th-232, U-235
Edad menor que la
Tierra, vida media más
corta, provienen
desintegración
primarios.
Producidos por los
rayos cósmicos sobre
elementos químicos.

28. SERIES RADIACTIVAS
Primarios Secundarios Inducidos
Los núcleos provienen de un mismo átomo inicial y por
desintegraciones sucesivas acaban en uno estable
En una serie o familia radiactiva…
Los núcleos pueden clasificarse en
Formación de la Tierra,
vida media muy larga,
U-238, Th-232, U-235
Edad menor que la
Tierra, vida media más
corta, provienen
desintegración
primarios.
Producidos por los
rayos cósmicos sobre
elementos químicos.

29. SERIES RADIACTIVAS
Animación

30. SERIES RADIACTIVAS
Animación

31. ¿Cuántos núcleos se desintegran?

32. ¿Cuántos núcleos se desintegran?
 En una muestra de isótopos radiactivos no se puede
predecir que núcleo se desintegrará  Carácter
probabilístico propio de los fenómenos cuánticos.

33. ¿Cuántos núcleos se desintegran?
 En una muestra de isótopos radiactivos no se puede
predecir que núcleo se desintegrará  Carácter
probabilístico propio de los fenómenos cuánticos.
 Se desintegran de tal forma que después de un
determinado tiempo (período de semidesintegración
T1/2), queda la mitad de la muestra.

34. ¿Cuántos núcleos se desintegran?
 En una muestra de isótopos radiactivos no se puede
predecir que núcleo se desintegrará  Carácter
probabilístico propio de los fenómenos cuánticos.
 Se desintegran de tal forma que después de un
determinado tiempo (período de semidesintegración
T1/2), queda la mitad de la muestra.
Tratemos de deducir la ley de
desintegración radiactiva …

35. A.20. Teniendo en cuenta lo anterior, calcular el número de núcleos
de una sustancia radiactiva que quedarán sin desintegrar cuando
hayan transcurrido 60 años. El periodo de semidesintegración es 10
años y el número inicial de núcleos, 64·1040. Realizar la
representación gráfica del número de núcleos sin desintegrar en
función del tiempo. Extraer conclusiones.

36. A.20. Teniendo en cuenta lo anterior, calcular el número de núcleos
de una sustancia radiactiva que quedarán sin desintegrar cuando
hayan transcurrido 60 años. El periodo de semidesintegración es 10
años y el número inicial de núcleos, 64·1040. Realizar la
representación gráfica del número de núcleos sin desintegrar en
función del tiempo. Extraer conclusiones.
Transcurridos 10 años quedarán 32·1040
Transcurridos 20 años quedarán 16·1040
Transcurridos 30 años quedarán 8·1040
Transcurridos 40 años quedarán 4·1040
Transcurridos 50 años quedarán 2·1040
Transcurridos 60 años quedarán 1·1040
Animación 1 Animación 2

37. La ley de desintegración radiactiva
El número final de átomos N,
depende de:
La constante de desintegración
radiactiva λ, propia de cada núcleo
(relacionada con el período de
semidesintegración).
Del número inicial de átomos N0.

38. Deducción
El número de núcleos desintegrados, -dN, en un tiempo, dt, es proporcional ( ) al número
de núcleos en un determinado instante, N, y al intervalo de tiempo considerado dt.

39. Deducción
El número de núcleos desintegrados, -dN, en un tiempo, dt, es proporcional ( ) al número
de núcleos en un determinado instante, N, y al intervalo de tiempo considerado dt.
Todo lo que depende de N a un lado de la expresión e integramos a ambos lados de la
expresión, entre N0 y N, y entre t0 y t

40. Deducción
El número de núcleos desintegrados, -dN, en un tiempo, dt, es proporcional ( ) al número
de núcleos en un determinado instante, N, y al intervalo de tiempo considerado dt.
Todo lo que depende de N a un lado de la expresión e integramos a ambos lados de la
expresión, entre N0 y N, y entre t0 y t
Resolvemos la integral definida y tomamos t0 =0

41. Deducción
El número de núcleos desintegrados, -dN, en un tiempo, dt, es proporcional ( ) al número
de núcleos en un determinado instante, N, y al intervalo de tiempo considerado dt.
Todo lo que depende de N a un lado de la expresión e integramos a ambos lados de la
expresión, entre N0 y N, y entre t0 y t
Resolvemos la integral definida y tomamos t0 =0
Aplicando la exponencial a ambos términos de la ecuación y despejando N:

42. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.

43. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.
El período de semidesintegración (t= T1/2) es el tiempo en el que el número de
núcleos se reduce a la mitad (N=N0/2)

44. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.
El período de semidesintegración (t= T1/2) es el tiempo en el que el número de
núcleos se reduce a la mitad (N=N0/2)

45. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.
El período de semidesintegración (t= T1/2) es el tiempo en el que el número de
núcleos se reduce a la mitad (N=N0/2)

46. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.
El período de semidesintegración (t= T1/2) es el tiempo en el que el número de
núcleos se reduce a la mitad (N=N0/2)

47. A.21. Determinar la relación entre el periodo de semidesintegración
y la constante radiactiva.
 Cuanto mayor sea el periodo de un átomo, más despacio se desintegra y, por
tanto, menor será .
 El período puede tomar valores entre 10-22 s y 1028 s (1021 años)
 Una constante de =3 s-1 nos dice que en cada segundo se desintegran 3
átomos.
El período de semidesintegración (t= T1/2) es el tiempo en el que el número de
núcleos se reduce a la mitad (N=N0/2)

48. La vida media,
Es el promedio de vida de un núcleo antes de desintegrarse.

49. Datación con Carbono 14
Animación

50. A.22. Una muestra de carbón de madera procedente de un tronco
de ciprés de la tumba de un rey egipcio tiene una relación C-14/C-
12, que es el 54,2% de la que presenta el carbón actual. Determinar
aproximadamente cuándo se cortó el ciprés.

51. A.22. Una muestra de carbón de madera procedente de un tronco
de ciprés de la tumba de un rey egipcio tiene una relación C-14/C-
12, que es el 54,2% de la que presenta el carbón actual. Determinar
aproximadamente cuándo se cortó el ciprés.