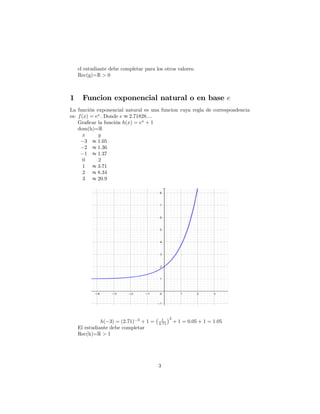
Este documento describe las funciones exponenciales, incluyendo sus características clave como su dominio en los números reales y recorrido en los números reales positivos. Explica que la función exponencial natural se define como f(x)=ex y proporciona ejemplos de graficar funciones exponenciales como f(x)=2x, g(x)=1/2x+1 y h(x)=ex+1. También incluye una tarea con preguntas sobre funciones exponenciales y una aplicación para calcular la población futura de una ciudad.

1. FUNCION EXPONENCIAL
Se conoce como función exponencial a la funcion f de variable real cuya
regla de correspondencia es:
f(x) = ax
, a 2 R+
y a 6= 1:
En esta de…nición, considere que a representa la base y x el exponente.
Por ejemplo:
f(x) = 2x
g(x) = 1
3
x
Antes de realizar las grá…cas funciones exponenciales, analicemos algunas
caracteristicas de f(x) = ax
, a 2 R+
y a 6= 1:
1.- El dominio de la funcion es todo el conjunto de los números reales (R)
2.- Su recorrido el el conjunto de los núemros reales mayores que cero (R > 0)
3.- Si a = 0; entonces f(0) = a0
= 1;lo que signi…ca que la funcion exponen-
cial pasa por el P(0; 1)
4.- El eje de las "x" es una asintota horizontal
5.- si a > 1;la función exponencial es creciente o si 0 < a < 1;la función
exponencial el decreciente, etc.
Gra…ca de funciones exponenciales.
Gra…car la función : f(x) = 2x
+ 1
Dom(f)=R
Tabla de valores
x y
3 9
8
2 5
4
1 3
2
0 2
1 3
2 5
3 9
f( 3) = 2 3
+ 1 = 1
2
3
+ 1 = 1
8 + 1 = 1+8
8 = 9
8
El estudiante debe completar para los otros valores.
rec(f)=R > 1
2.- gra…car la función: g(x) = 1
2
x+1
dom(g)=R
x y
3 4
2 2
1 1
0 1
2
1 1
4
2 1
8
3 1
16
g( 3) = 1
2
3+1
= 1
2
2
= 22
= 4
1

2. 2

3. el estudiante debe completar para los otros valores.
Rec(g)=R > 0
1 Funcion exponencial natural o en base e
La función exponencial natural es una funcion cuya regla de correspondencia
es: f(x) = ex
: Donde e t 2:71828::::
Gra…car la función h(x) = ex
+ 1
dom(h)=R
x y
3 t 1:05
2 t 1:36
1 t 1:37
0 2
1 t 3:71
2 t 8:34
3 t 20:9
h( 3) = (2:71) 3
+ 1 = 1
2:71
3
+ 1 = 0:05 + 1 = 1:05
El estudiante debe completar
Rec(h)=R > 1
3

4. 2 Tarea:
1.- Ya antes se dijo que para las funciones exponenciales f(x) = ax
, el valor de
a no debe ser igual 1
a) cuando a = 1; ¿como se ve la gra…ca de f(x) = ax
?
b) Cuando a = 1; ¿ f(x) = ax
;es una función?
2.- Gra…que las funciones:
f(x) = 1
2
x
+ 2; g(x) = 2x+2
y h(x) = ex
Aplicaciones .
3.- La poblacion futura esperada de una ciudad que actualmente tiene de
350000 habitantes, puede aproximarse mediante la formula y = 350000(1:4)- 0:2t
, donde t es el numero de años a partir de hoy. Determine el cuantos habitantes
tendra la ciudad dentro de 30 años.
MSc. Luis Pilataxi
Docente
4