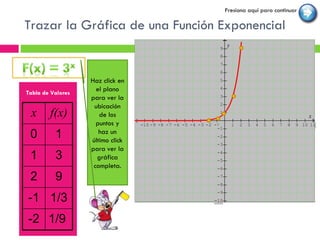
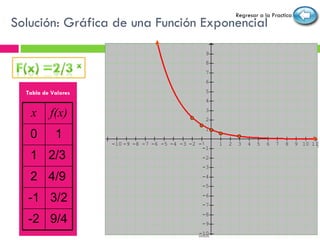
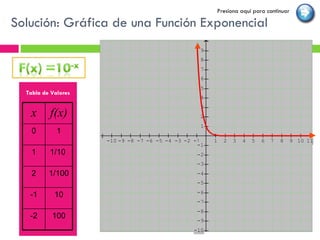
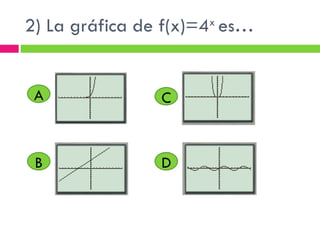
Este documento proporciona una introducción a las funciones exponenciales. Define funciones exponenciales, explora sus propiedades como ser crecientes o decrecientes dependiendo de la base, y muestra cómo graficarlas y resolver ecuaciones exponenciales. También presenta aplicaciones como el interés compuesto, crecimiento poblacional y decaimiento radiactivo. El documento concluye con una pre-prueba, la lección, ejercicios de práctica y una post-prueba para evaluar la comprensión del estudiante.
Demostraciones de teoremas acerca de límitesJames Smith
Los teoremas acerca de límites de funciones básicas nos proporcionan una estucha de herramientas con las que podemos encontrar límites de funciones compuestas y complejos. En este documento, se demuestran seis de los teoremas más útiles, para luego usarlos en la resolución, paso a paso, de un problema un poco complicado.
Demostraciones de teoremas acerca de límitesJames Smith
Los teoremas acerca de límites de funciones básicas nos proporcionan una estucha de herramientas con las que podemos encontrar límites de funciones compuestas y complejos. En este documento, se demuestran seis de los teoremas más útiles, para luego usarlos en la resolución, paso a paso, de un problema un poco complicado.
Resúmen hecho por Calculisto.com para la matéria de límites, sea para el curso de cálculo diferencial y integral o para el de matemáticas, ese es de lejos el mejor resúmen, con todas las fórmulas y explicaciones cortas y directas
Instrucciones del procedimiento para la oferta y la gestión conjunta del proceso de admisión a los centros públicos de primer ciclo de educación infantil de Pamplona para el curso 2024-2025.
ROMPECABEZAS DE ECUACIONES DE PRIMER GRADO OLIMPIADA DE PARÍS 2024. Por JAVIE...JAVIER SOLIS NOYOLA
El Mtro. JAVIER SOLIS NOYOLA crea y desarrolla el “ROMPECABEZAS DE ECUACIONES DE 1ER. GRADO OLIMPIADA DE PARÍS 2024”. Esta actividad de aprendizaje propone retos de cálculo algebraico mediante ecuaciones de 1er. grado, y viso-espacialidad, lo cual dará la oportunidad de formar un rompecabezas. La intención didáctica de esta actividad de aprendizaje es, promover los pensamientos lógicos (convergente) y creativo (divergente o lateral), mediante modelos mentales de: atención, memoria, imaginación, percepción (Geométrica y conceptual), perspicacia, inferencia, viso-espacialidad. Esta actividad de aprendizaje es de enfoques lúdico y transversal, ya que integra diversas áreas del conocimiento, entre ellas: matemático, artístico, lenguaje, historia, y las neurociencias.
6. Propiedades de las Funciones Exponenciales 1. Las funciones exponenciales pasan por el punto (0,1). 5. El dominio es el conjunto de los números reales. 4. El eje de x es una asíntota horizontal. 2. Si a (base) < 0 la función es decreciente. 3. Si a (base) > 0 la función es creciente. 7. Las funciones exponenciales son uno a uno. 6. El alcance es el conjunto de números reales positivos. Volver al índice Presiona aquí para continuar
7. Trazar la Gráfica de una Función Exponencial Podemos trazar la gráfica usando : Escoge entre tabla de valores y calculadora gráfica haciendo un click encima del que deseas. Volver al índice Presiona aquí para continuar x f(x) Tabla de Valores Calculadora Gráfica
![Índice ,[object Object],Presiona aquí para comenzar Objetivos Evaluación Tutorial Introducción Instrucciones Propósito Carta al Estudiante](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)