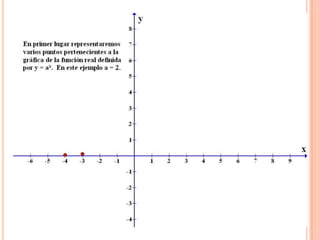
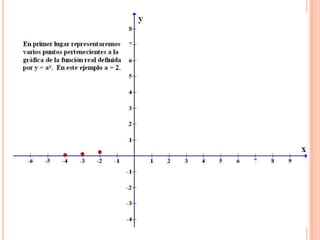
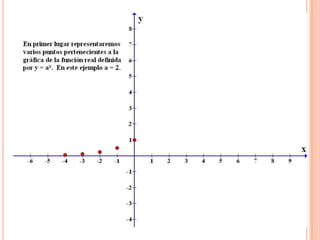
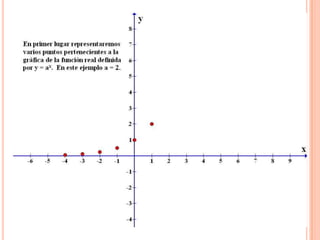
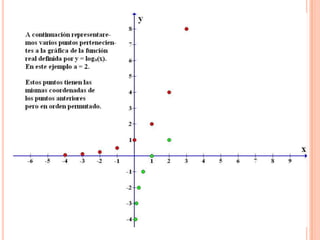
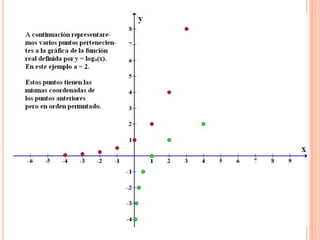
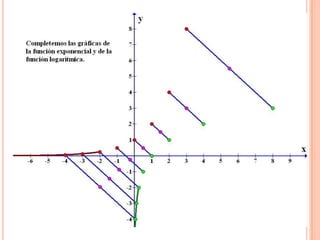
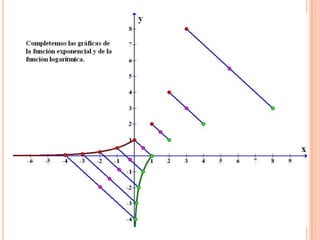
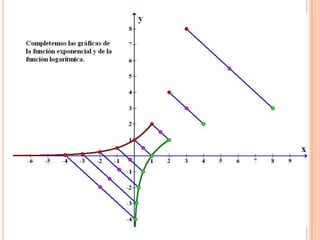
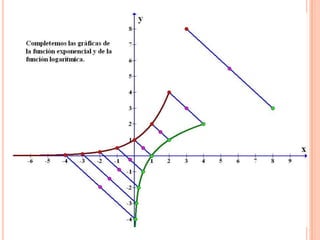
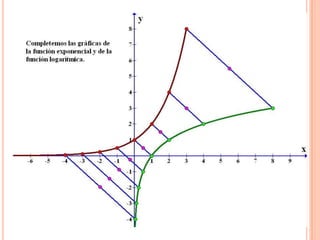
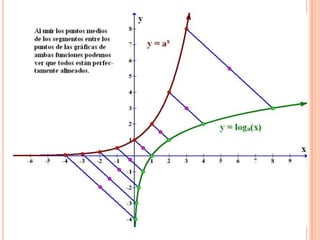
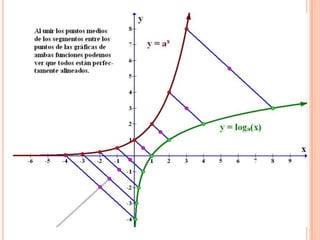
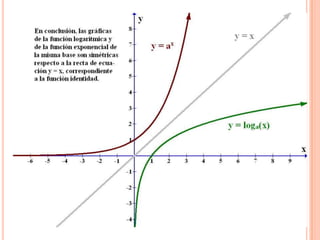
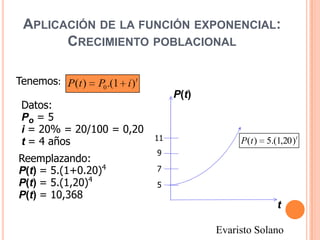
Este documento describe las funciones exponenciales y logarítmicas. Explica cómo graficar funciones exponenciales de la forma f(x)=ax con a>1 y 0<a<1, así como funciones logarítmicas de la forma f(x)=loga(x) con a>1 y 0<a<1. También presenta ejemplos de aplicaciones de estas funciones para modelar crecimiento poblacional.

1. FUNCIONES
EXPONENCIALES Y
LOGARÍTMICAS
Grupo N° 5
Sección 31

2. FUNCIONES EXPONENCIALES
f:
a [ g ( x )]
/ f ( x)
Dom [ f ( x )]
Dom [ g ( x )]
Caso I :
a
a
(0;
a>1
{1}
)
a
1
f:
/ f ( x)
2x
f :
/ f ( x)
ex
f:
/ f ( x)
3x
f:
/ f ( x) e
2
2x 1
x
Klinsmann Vivas

3. FUNCIONES EXPONENCIALES
f:
a [ g ( x )]
/ f ( x)
Dom [ f ( x )]
Dom [ g ( x )]
Caso II :
a
a
(0;
0<a<1
{1}
)
a
1
f:
/ f ( x)
( 12) x
f:
/ f ( x)
( 1e ) x
f:
/ f ( x)
( 13) x
f:
/ f ( x) ( e )
1
2
2x 1
x
Klinsmann Vivas

4. f :
/ f ( x)
2x
Cómo graficar la función exponencial f(x) = ax, con a > 1.
Por ejemplo:
x
y
-3
⅛
-2
¼
-1
½
0
1
1
2
2
4
3
y = 2x
8
y = 2x
Eduardo Mijares

5. CARACTERÍSTICAS GENERALES
i.
f :
/ f ( x)
DDom[f(x)] = x ∊ .
El
dominio de la función son
todos los números reales.
ii.
RRgo[f(x)] = x ∊
rango son los
reales positivos.
iii.
PPx = ∄.
Es asintótica al eje X.
iv.
PPy = (0,1).
v.
LLa función es Creciente
para todo valor x a lo largo
de su dominio.
vi.
ff(x) > 0 | ⦡x ∊ .
La
función es positiva a lo largo
de su domino.
2x
y = 2x
+
.
Su
números

6. Otras funciones con
y = 5x
y = 3x
> 1 (crecientes):
y = 2x

7. f:
/ f ( x)
( 12) x
Cómo graficar la función exponencial f(x) = ax, con 0 < a < 1.
Por ejemplo:
x
y
-3
8
-2
4
-1
2
0
1
1
½
2
¼
3
y = (½)x
⅛
y = (½)x
María Valeria Aguilera

8. CARACTERÍSTICAS GENERALES
i.
ii.
f:
/ f ( x)
DDom[f(x)] = x ∊
.
El dominio de la función son
todos los números reales.
RRgo[f(x)] = x ∊
rango son los
reales positivos.
iii.
PPx = ∄.
Es asintótica al eje X.
iv.
PPy = (0,1).
v.
LLa función es Decreciente
para todo valor x a lo largo
de su dominio.
vi.
ff(x) > 0 | ⦡x ∊ .
La
función es positiva a lo largo
de su domino.
( 12) x
y = (½)x
+
.
Su
números

9. Otras funciones con 0 <
y = (½)
x
y = (⅓)x
< 1 (decrecientes):
y = (⅕)
x

10. La función real de variable real que no necesariamente es
una función exponencial:
y = k . ax+b + c
y = -3. (½)x+2 +3
Klinsmann Vivas

11. APLICACIÓN DE LA FUNCIÓN EXPONENCIAL:
CRECIMIENTO POBLACIONAL
Una compañía nueva con 5 empleados espera que el
número de empleados crezca a una tasa de 20% cada año.
Determine el número de empleados dentro de 4 años.
Tenemos: P (t )
P0 .(1 i )t
Elementos de la fórmula:
• Cantidad de empleados en función del tiempo ⇒ P(t)
• Cantidad conocida de empleados ⇒ Po = 5
• Porcentaje de crecimiento ⇒ i = 20% anual
• Tiempo ⇒ t = 4 años
Evaristo Solano

12. APLICACIÓN DE LA FUNCIÓN EXPONENCIAL:
CRECIMIENTO POBLACIONAL
Tenemos: P (t )
P0 .(1 i )t
Datos:
Po = 5
i = 20% = 20/100 = 0,20
t = 4 años
Reemplazando:
P(t) = 5.(1+0.20)4
P(t) = 5.(1,20)4
P(t) = 10,368
P(t)
11
P (t )
5.(1,20 )t
9
7
5
t
Evaristo Solano

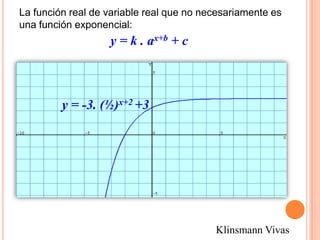
13. FUNCIONES LOGARÍTMICAS
f:
/ f ( x)
Dom [ f ( x )] : {x
log a [ g ( x )]
/ g ( x)
0}
Caso I :
a
a
(0;
a>1
{1}
)
a
f:
1
f:
/ f ( x)
/ f ( x)
f:
f:
log 2 x
log e x
/ f ( x)
/ f ( x)
ln x
log 3 ( x 2)
ln( 2 xx 1 )
Klinsmann Vivas

14. FUNCIONES LOGARÍTMICAS
f:
/ f ( x)
Dom [ f ( x )] : {x
log a [ g ( x )]
/ g ( x)
0}
Caso II :
a
a
(0;
0<a<1
{1}
)
a
f:
/ f ( x) log 12 x
f:
1
/ f ( x) log 1e x
f:
/ f ( x) log 13 ( x 2)
f:
/ f ( x) log 1e ( 2 xx 1 )
Klinsmann Vivas

15. f:
/ f ( x)
log 2 x
Cómo graficar la función logarítmica f(x) = loga(x), con a > 1.
Por ejemplo: y = log2 x
x
y
⅛
-3
¼
-2
½
-1
1
0
2
1
4
2
8
2y= x
3
y = log2 (x)
Orguimar Barrios

16. CARACTERÍSTICAS GENERALES
i.
f:
DDom[f(x)] = x ∊ +.
El
dominio de la función son
todos los números reales
positivos.
ii.
RRgo[f(x)] = x ∊ .
Su
rango son los números
reales.
iii.
PPx = (1,0).
iv.
PPy = ∄.
asintótica al eje Y.
v.
LLa función es Creciente
para todo valor x a lo largo
de su dominio.
vi.
ff(x) < 0 | ⦡x ∊ (0 ; 1).
vii.
ff(x) > 0 | ⦡x ∊ (1 ; +∞).
/ f ( x) log 12 x
y = log2 (x)
Es

17. Otras funciones con a > 1 (crecientes):
y = log2 x
y = log3 x
y = log5 x

18. f:
/ f ( x) log 12 x
Cómo graficar la función logarítmica f(x) = loga(x), con 0 < a < 1.
Por ejemplo: y = log(½) x
x
y
8
-3
4
-2
2
-1
1
0
½
1
¼
2
⅛
(½) y = x
3
y = log(½) x
Carlos Escobar

19. CARACTERÍSTICAS GENERALES
i.
f:
DDom[f(x)] = x ∊ +.
El
dominio de la función son
todos los números reales
positivos.
ii.
RRgo[f(x)] = x ∊ .
Su
rango son los números
reales.
iii.
PPx = (1,0).
iv.
PPy = ∄.
asintótica al eje Y.
v.
LLa función es Decreciente
para todo valor x a lo largo
de su dominio.
/ f ( x) log 12 x
vi.
f(x) > 0 | ⦡x ∊ (0 ; 1).
vii.
f(x) < 0 | ⦡x ∊ (1 ; +∞).
Es

20. Otras funciones con 0 < a < 1 (decrecientes):
y = log⅕ x
y = log⅓ x
y = log½ x

21. La función real de variable real que no necesariamente es
una función logarítmica:
y = k . loga (x – b) + c
y = - 3/2 . log3 (x + 2) + 1
Klinsmann Vivas

22. APLICACIÓN DE LA FUNCIÓN LOGARÍTMICA:
CRECIMIENTO POBLACIONAL
Si una comunidad que inicialmente tiene 200 habitantes
mayores de edad y tienen una tasa de crecimiento de 50%
anual. Determinar en cuanto tiempo alcanzara completar los
300 habitantes.
Pf
t
t log (1 k )
t log (1 k ) P
Tenemos: Pf P.(1 k )
i
Pi
Elementos de la fórmula:
• Cantidad final de habitantes ⇒ Pf = 300
• Cantidad conocida de habitantes ⇒ Pi = 200
• P = Pf / Pi
• Porcentaje de crecimiento ⇒ k = 50% anual
• Tiempo ⇒ t
Pedro Ramírez

23. APLICACIÓN DE LA FUNCIÓN LOGARÍTMICA:
CRECIMIENTO POBLACIONAL
Tenemos: Pf P.(1 k )
i
Datos:
Pf = 300
Po = 200
i = 50% = 50/100 = 0,50
t
t
log (1
Pf
k)
t
Pi
log (1
t
Reemplazando:
t = log(1+0,50)(300/200)
t
log( 32 ) P
t = log(1,50)(3/2)
t = log(3/2)(3/2) = 1
1 1.25 1.5 1.75
P
k)
P

24. FUNCIÓN EXPONENCIAL Y LOGARÍTMICA:
RELACIÓN ENTRE GRÁFICAS.
Las funciones logarítmicas y exponenciales
de la misma base son mutuamente inversas.
Esta relación afecta a sus respectivas gráficas
y produce una especial disposición de las
mismas en el plano cartesiano.
Para finalizar esta presentación veremos el
por qué de tal disposición de las gráficas de
estas dos funciones trascendentes.

74. "Mil cosas avanzan. Novecientas noventa y
nueve retroceden. Esto es el progreso".
Henri Frederick Amiel (1821-1881); escritor y profesor suizo.
GRACIAS POR SU
ATENCIÓN.