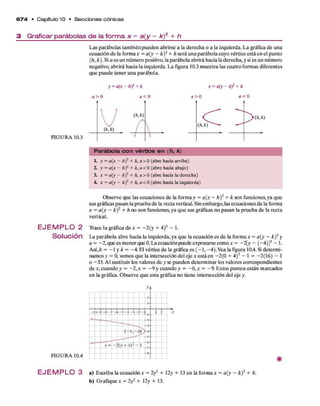
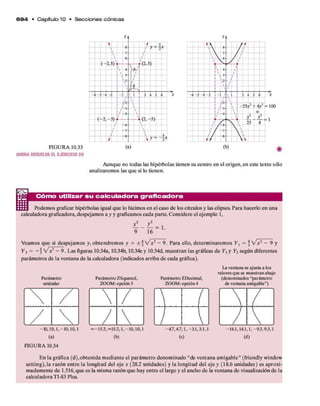
Este documento presenta información sobre el libro de texto "Álgebra intermedia" de Allen R. Angel. Incluye los créditos de los autores, traductores, revisores y la editorial Pearson responsable de la publicación. Además, contiene la portada, la dedicatoria, el contenido con los 11 capítulos que componen el libro y la información bibliográfica.














![Prefacio • x v
Ejercidos de repaso acumulativo Todos los conjun
tos d e ejercicios (salvo los dos prim eros) contienen p re
guntas referentes a secciones y capítulos anteriores. Los
ejercicios planteados en la sección “Ejercicios d e repaso
acumulativo” refuerzan los tem as estudiados con anterio
ridad, y ayudan a retener el m aterial ya analizado mien
tras se estudia el nuevo. Para beneficio d e los estudiantes,
los ejercicios d e repaso acum ulativo indican, p o r m edio
de corchetes com o [3.4], la sección en donde se revisó el
material.
Ejercicioscon icono de vídeo Los ejercicios q u e se re
suelven con detalle en las videocintas aparecen m arcados
con el icono « , lo cual perm ite una identificación fácil y
rápida. E ste m aterial se adquiere p o r separado y se en
cuentra en idiom a inglés.
Actividad ©n equipo Muchos conjuntos d e ejercidos
tienen ejercicios de “Actividad en equipo” q u e conducen a
interesantes discusiones en grupo. A lgunos estudiantes
aprenden m ejor en un am biente cooperativo,y estos ejer
cicios perm itirán q u e los alum nos hablen d e m atem áticas
entre ellos.
Resumen del capítulo Al final d e cada capítulo se
m uestra un resum en q u e incluye “Térm inos y frases im
portantes”.
Ejercicios de repaso del capítulo Al final d e cada
capítulo hay ejercicios d e repaso q u e abarcan todos los
temas analizados en el mismo. Los núm eros en color rojo
y en tre corchetes sirven p ara identificar la sección en
donde se presen tó el m aterial p o r p rim era vez.
Exámenes de práctica del capítulo El am plio exa
m en q u e se encuentra al final de cad a capítulo perm ite
q u e los estudiantes determ inen q u é tan preparados es
tán p ara presentar el exam en real d e cada p arte del cu r
so. Las respuestas a las preguntas del exam en d e repaso
acum ulativo aparecen en seguida del m ism o, d e m odo
q u e se p u ed an verificar ráp id am en te sus resultados.
D espués d e cad a respuesta se incluye una leyenda en
tre corchetes, com o [Sec. 4.2, Obj. 5], p ara indicar la sec
ción y el objetivo en d o n d e se e stu d ió el m aterial
correspondiente.
Examen de repaso acumulativo El propósito d e es
tos exámenes,q u e aparecen al final d e cada capítulo (salvo
en el prim ero), es verificar los conocim ientos adquiridos
respecto del m aterial analizado desde el principio del li
bro hasta el capítulo en el q u e se encuentre. Puede utili
zar estos exám enes como repaso o com o preparación para
el exam en final. A l igual q u e los “Ejercicios d e repaso
acum ulativo”, estos exám enes sirven p ara reforzar lo
aprendido de los tem as analizados con anterioridad. Las
respuestas a las preguntas del exam en d e repaso acum ula
tivo aparecen en seguida del mismo, d e m odo q u e se p u e
d an verificar rápidam ente sus resultados. D espués de
cada respuesta se incluye una leyenda en tre corchetes,
com o [Sec. 4.2, Obj. 5], para indicar la sección y el objeti
vo en donde se estudió el m aterial correspondiente.
Respuestas E l libro proporciona las respuestas a los
problem as de núm ero im par d e cada conjunto d e ejerci
cios, así com o las respuestas a todos los ejercicios d e las
secciones d e uso d e calculadora graficadora, los “Ejerci
cios d e repaso acum ulativo”, los ejercicios d e repaso, los
exám enes y los exám enes d e repaso acumulativo del capí
tulo. Por otro lado, no se d a la respuesta a los ejercicios de
“A ctividad en equipo”, y a q u e su intención es q u e los
estudiantes logren acuerdos al respecto.
M o d o s d e e n se ñ a n za
El constante refuerzo d e los conceptos d a p o r resultado
una m ayor com prensión y retención del m aterial p o r p ar
te d e sus estudiantes. Por otro lado, el form ato y la legibi
lidad d e este libro lo hacen apropiado p ara m uchos estilos
de enseñanza, p o r ejemplo:
• clase institucional (clásica)
• educación a distancia
• aprendizaje autodidacta
• clase modificada
• estudio en equipo o cooperativo
• laboratorio d e enseñanza
C a m b io s en la sexta edición
Cuando escribí la sexta edición, tom é en cuenta muchos
com entarios y revisiones d e los estudiantes y profesores.
Quiero agradecer a todos aquellos q u e hicieron sugeren
cias p ara m ejorar este libro. Tam bién quiero agradecer a
la gran can tid ad d e profesores y estudiantes q u e escri
bieron p ara inform arm e lo m ucho q u e disfrutaron y
aprendieron del texto.
Algunos d e los cam bios realizados en esta sexta edi
ción son:
• E l capítulo d e raíces, radicales y núm eros com plejos
se reorganizó y reescribió p ara darle m ayor claridad.
A hora puede leerse d e m anera más fluida.
• Se hizo m ayor hincapié en la geom etría; en el texto
hay m ás ejem plos y ejercicios relacionados con esta
disciplina.
• Se agregó una gran variedad d e problem as a los con
juntos d e ejercicios d e todo el libro. E n general, se am
pliaron d e m anera notable.
• E n secciones seleccionadas se agregaron problem as
d e m ayor com plejidad al final d e los conjuntos de
ejercicios.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-15-320.jpg)









![Problem as d e reto
Los problemas de la sección Reto
estimulan el interés de los
estudiantes con ejercicios más
demandantes o difíciles en los
aspectos conceptual o de realización.
Actividad en equipo
Las actividades en equipo
proporcionan a los estudiantes
oportunidades para desarrollar el
aprendizaje colaborativo.
Ejercicios d e repaso
acumulativo
Los Ejercicios de repaso acumulativo
refuerzan los temas tratados con
anterioridad. Estos ejercicios indican
las secciones en donde se explicó el
material.
5 2 • C a p JtiJo 1 • C o n c e p to s b á s ic o s
R eto
H t la sección 72 aprenderá que las reglas de lo s ex ponentes que acabam os de presentar,tam bién se aplican cuando Ios ex ponentes
son números racionales. Con base en esta Inform ación y en las reg/as de Ios exponentes, resuelva cada expresión
- $r - m - (*
- g? - m
Actividad e n eq u ipo______________
Analice y responda en equipo el ejercido 143.
M3. C entavos qu e crecen B día 1 se le da un centavo. Cada
uno de lo s días que siguen se le dará e l doble d e la canti
dad que se le entregó el d b anterior.
a) Escriba1» cantidades que le darbn en cada uno de lo s
primeros 6 días.
b) Señale rata uno de estos números com o una expresión
exponencial con una base de 2.
c) Buscando un patrón determine una expresión ex p o
nencial para e l núm ero de centavos que recibirá el
día 10.
Ejercicios d e rep aso acum ulativo
[ 1 ¿ ] 144.Si A - { 3 . 4, 6) y B - { 1 . 2. 5. 8 ). determine
a )A U f iy b)<4 C fl.
145.1ustre e l siguiente conjunto en la recu numérica:
{*|-3 * x < 2 ) .
d) Eacxiha unaexpresión exponencial general para e l nú-
merode centavos que redará e l día n
el Escriha una expratión exponencial para e l número de
centavos que recibirá e l d b 30.
f) Q d cu led valor de b expresión en taparle e ) S i tiene
calculadora, utiícela.
V) Determine la cantidad,en pesos, que obtuvo com o re-
s u lu d o e n b parte I),
h) Escriba unaexpresiónexponencbl general para el nú
mero d e p a o s que re d a r á en e l día n.
[1.4] MóXblcule: 6 + |12 | + |- 3 | - 4 -2 1.
147ívaluate S^=T25.
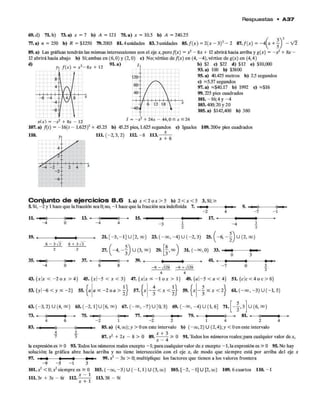
1.6 NO TAC IÓ N C IENTIFICA
1 E s c rb ir n ú m e ro s e n n o tación científica.
2 C a m b ia r n ú m e ro s e n no tació n clentfflca a fo rm a d ecim a l.
3 U s a r no tació n clentfflca e n la resolución d e p ro blem a s.
1 Escribir números en notación clentfflca____________________________________________
C on m u ch a frecu en cia, lo s cien tíficos c ingenieros tien en q u e trabajar co n núm eros
m uy gran d es y m uy p e q u e ñ o s Por ejem p lo, la frecuencia d e la señ a l d e u n rad io FM
p u e d e ser d e 14,200,000,000 hertz (o c ic lo s p o r seg u n d o ), y e l d iám etro d e u n átom o
d e h id rógeno e s d e alred ed or d e 0.0000000001 m etros D e b id o a la dificultad q u e im
p lica trabajar c o n m uchas ceros, a m enu d o las cien tíficos exp resan tales num eres co n
exp on en tes. Por ejem p lo, e l n ú m ero 14,200,000,000 p od ría escribirse co m o 1.42 X 10'°
y 0.0000000001 com o 1 X 10“ '".Esta representación abreviada s e co n o ce com o n o ta d ó n
d e n tífica. E n n o ta d ó n cien tífica, b s núm eros ap arecen com o un núm ero m ayor o igual
a 1 y m en or q u e 10, m u ltip licad o p o r alg u n a p o ten cia d e 10. E l ex p o n en te d e 10 d e
b e ser u n en te ro . C u a n d o una p o ten cia d e 10 n o tie n e co e ficien te n u m érico , co m o
A P á g in a 5 2
X X V](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-25-320.jpg)















![S e cció n 1.2 • C o n ju n to s y o tro s c o n c e p to s básicos • 1 3
e) Los núm eros irracionales son núm eros reales q u e no son racionales. Los siguientes
núm eros son irracionales
V7,-VIT,-7r
f ) Todos los núm eros del conjunto son núm eros reales. L a unión d e los núm eros ra
cionales y los núm eros irracionales conform a el conjunto d e los núm eros reales.
« . « « a ™ » - 3 , 0 , f . 2 . 2 5 , ^ , - V I l , f , 5 , 7 . 1 , - 1 7 , , #
No todos los núm eros son núm eros reales. Algunos d e los núm eros q u e estudia
rem os más adelante y q u e no son núm eros reales, son núm eros com plejos y núm eros
imaginarios.
M atem áticas en a c c ió n
Conjuntos bien definidos y conjuntos difusos
Al tipo d e conjuntos acerca d e los q u e usted está apren
diendo en este capítulo, m uchas veces se les conoce co
mo conjuntos bien definidos. U n elem ento es o no es
miembro d e un conjunto bien definido. Es evidente que
Q es un elem ento del conjunto {Tt R, Q, F] y q u e B no
k) es. M ás allá del mundo d e las matem áticas, podem os
reconocer q u e la afirmación: “A braham Lincoln es un
elem ento del conjunto d e todos los presidentes d e Es-
lados U nidos”, refleja el concepto d e los conjuntos bien
definidos.
Ahora piense en el conjunto d e todos los hom bres
con cabellera com pleta, y digam os q u e una cabellera
com pleta es aquella q u e cuenta con 100 mil o más ca
bellos. Federico se levanta en la m añana con 100 mil
cabellos en su cabeza,d e modo q u e él pertenece al con
junto. Al tom ar una ducha,cinco cabellos caen de su cabe
za y se van p o r el desagüe. A hora él no pertenece al
conjunto. Bueno, eso es correcto, aunque suene tonto.
U na categorización rígida com o ésta no sería muy útil
para una em presa q u e reúne informaciónpara com ercia
lizar una línea d e productos p ara el cuidado del cabello.
E n 1965 fue mencionado p o r prim era vez el con
cepto d e conjunto difuso. P ara explicarlo d e m anera
sencilla, digam os q u e un elem ento q u e form a p arte de
un conjunto difuso tiene cierto grado d e pertenencia a
él. Volviendo al ejem plo d e Federico, si un conjunto di
fuso fuese definido com o “todos los hom bres con una
cabellera com pleta”,cuando Federico se levantó e n la
m añana era m iem bro d e ese conjunto con un valor de
1 (o d e 100 p o r ciento). D espués d e la ducha, Federico
seguía perteneciendo en ese conjunto, pero con un va
lor de, digamos, 0.999.
E l razonam iento asociado a los conjuntos difusos,
gobernado p o r las reglas d e la lógica difusa, es la base
para que los program as d e cómputo logren el reconoci
miento d e patrones, por ejem plo el reconocimiento de
voz. La pronunciación d e un ganadero de M onterrey,en
México, difiere considerablem ente d e la d e un corredor
efe bolsa d e M adrid, E spaña Para reconocer la diferen
cia, el program a aplicará una gran cantidad d e pruebas
de la lógica difusa p ara determ inar el grado hasta el que
un sonido coincide con otro almacenado en su base de
datos de conjuntos difusos. Al no insistir en que haya una
correspondencia exacta p ara cualquier letra o sílaba
—por ser difusa— ,el program a puede “entender” el ha
bla hum ana con sorprendente precisión.
C o n j u n t o d e e j e r c i c i o s 1.2
Ejercicios conceptuales
L ¿Qué es una variable?
2. ¿Qué es una expresión algebraica?
3. ¿Qué es un conjunto?
4. ¿Cómo les llamamos a las partes que conforman un con
junto?
5. ¿Qué es un conjunto vacíoo conjunto nulo?
6. H conjunto de los números naturales o números para con
tar, ¿es un conjunto finito o infinito? Explique.
7. Liste los cinco símbolos de desigualdad y explique cómo
sí lee cada uno de ellos.
8. Proporcione un ejemplo de un conjunto vacío.
9. Liste el conjunto de enteros entre 2 y 7.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-41-320.jpg)
![1 4 • Capítulo 1 • C o n c e p to s básicos
10. Liste el conjunto de enteros entre -1 y 3 inclusive.
V 1L Explique por qué todos los números enteros son también
“ números racionales.
12. Describa los números para contar, los números enteros no
negativos, los números enteros, los números racionales, los
números irracionales y los números reales. Explique las
relaciones entre los conjuntos de números.
En los ejercicios 13a 22, indique si cada afirmación es verdadera
o falsa.
13. Todos los números naturales son enteros no negativos.
14. Algunos números racionales son enteros.
15. Todos los números enteros no negativos son números na
turales.
16. Todos los números racionales son enteros.
17. Todos los números enteros son números racionales.
18. La unión del conjunto de los números racionales y el con
junto de los números irracionales forma el conjunto de los
números reales.
19. La interseccióndel conjunto de los números racionales y el
conjunto de los números irracionales es un conjunto vacío.
20. Elconjunto de los números naturales es un conjunto finito.
2L El conjunto de los números enteros entre ir y 4 es un con
junto vacío (nulo).
22. El conjunto de los números irracionales entre 3 y n es un
conjunto infinito.
Problemas de aplicación
Escriba < o > en el área sombreada para hacer que la afirmación sea verdadera.
23. 3 ■ 4 24. - 1 B 5 25. - 3 ■ 0 26. - 1 ■ 1
27. - 1 ■ - 1.01 28.
co
1
■
■
'
T
Q. 29. - 5 ■ -3 30. -6 M - 1
3L -14.98 ■ -14.99 32. -3 .6 ■ -3.2 33. 1.1 ■ 1.9 34 -1.1 ■ -1.9
35. - ir M - 4 36. -7 8 0 ■ -655
- 4 - ! 38.
_ 4 . _ 5
7 9
En ¡os ejercicios39 a 48, escribacada conjunto en forma de lista.
39. A = { * |-1 < * < l y x e Z }
4 L C = {z z es un entero par mayor que 16y menor que
o igual a 20}
43. E = {xx < 3y x e W }
45. H = {xx es un entero no negativo múltiplo de 7}
47. / = {*|* > Oy x e Z )
49. Cbnsidereel conjunto {-3 , 4, f , 0, V 2 , V 8 , -1.23, %
¡ó]
Liste los elementos que son:
a) números naturales.
b) enteros no negativos.
c) enteros.
d) números racionales.
e) números irracionales.
f) números reales.
40. B = {y|y es un número natural impar menor
que 8}
42. D = {*|* > - 3 y * e Z }
44. F = {* i- 6 ^ - 15
5 T y't "}
46. L = {*|* es un entero mayor que -5}
48. K = {*|* es un entero no negativo entre 3 y 4}
50. Cbnsidere el conjunto {2, 4, -5.33, f , V 7, V 2, -100,
-7, 4.7}. Liste los elementos que son:
a) números enteros no negativos.
b) números naturales.
c) números racionales.
d) números enteros.
e) números irracionales.
f) números reales.
Determine A U B y A H B,para cada conjunto A y B.
5L A = {1,2, 3, 4, 5}, B = { 2 4 ,6 ,8 )
53. A = { -3 , - 2 , - 1 ,0 ) , B = { -1 ,0 ,1 ,2 }
55. A = { } , B = {2,4,6,8,10)
57. A = {0,10,20,30), B = {5,15,25}
59. A = {—1,0,1, e,i,ir}, B = { -1 ,0 ,1 }
52. A = { 1 ,2 ,3 } , B = {4,5,6}
54 >1 = { - 3 ,- 1 ,1 , 3}, B = { -4 , -3 , -2 , -1 , 0}
56. A = {2 4 ,6 } , B = {2 ,4 ,6, 8, ...}
58. A = {1, 3, 5},B = {1,3,5, 7, ...}](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-42-320.jpg)
![S e cció n 1.2 • C o n ju n to s y o tro s c o n c e p to s básicos * 1 5
Describa cada conjunto.
6L A = {1,2, 3,4, ...}
63. C = {0,3, 6, 9, ...}
65. B = { ...,- 5 ,- 3 ,- 1 ,1 , 3, 5, ...}
V 61 B = {2, 4, 6, 8, ...}
64. A - { a ,b , c , d , . .. ,z }
66. C - {Aguascalientes, Baja California,..., Zacatecas}
En los ejercicios 67 y 68, a) escriba cómo leería cada conjunto; b) escriba el conjunto en forma de lista.
67. A = {*|* < 8 y * e N } 68. B = {xx es una de las últimas cinco letras mayúsculas del
alfabeto castellano}
Ilustre cada conjunto en una recta numérica.
69. {xx > 0 } 70. {yy < 4}
71. {zz ^ 3} 72. {ww > -5 }
73. {pl~4 < p < 3} 74. {*1-1.67 < * < 5.02}
75. {qq > - l y q e N ) 76. {*|-1.90 < * < 2 . 1 y * e Z }
77. {rr < 7r y r e W] 78.
r i <-
csf y-
ce'v}
Exprese en notación de construcción de conjuntos cada conjunto de números indicado en las rectas numéricas.
79.
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
80.
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
8L
83.
85.
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
■ I I , -------
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
-2.5 4.2
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
87. « I l i » + + + » ? l l l -----
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
84.
- 4 ♦ » ♦ 1 ■
- 9 - 8 - 7 - 6 - 5 - 4
— - h
- 3 - 2
4
1 1 • 1
- 1 0 1 2
7 .6
H — -
3
- 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
* 1 !' 1
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
12 3
1— 1— t -
5
-----4—
10
■ -4— 1— 1— 1— -t— ►
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
Consulte el recuadro de la página II para recordar el significado de R, N, W ,Z,Q e I. Luego determine si el primer conjunto de cada
par es un subconjunto del segundo.
89. N ,W 90. W,Q
93. Q ,¡ 94. Q, R
Resolución de problemas
97. Construya un conjunto que contenga cinco números ra
cionales entre 1 y 2.
99. Determine dos conjuntos A y B tales que A U B = {2,4,
5 ,6 ,8 ,9 } y A n £ = {4,5,9}.
9L Z,Q 92. W ,N
95. /, R 96. Q ,Z
98. Cónstruya un conjunto que contenga cinco números ra-
aonales entre 0 y 1 .
100. Determine dos conjuntos A y B tales que A U 8 = {3,5,
7,8,9} y A C B = {5,7}.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-43-320.jpg)













![Sección 1.4 • O rd e n d e las o p e ra cio n e s • 2 9
Determine la diferencia en la balanza depagos per cápita entre los siguientes estados.
a) NM y CT b) OK y MI c) VA y NJ d) TX y CA
144 Pequeñas empresas La cámara de comercio de Guadala-
jara, en México, estudió el éxito y fracaso de nuevas pe
queñas empresas (con menos de cinco empleados) en su
ciudad. Al hacerlo, determinaron los gastos promedio en
que incurrieron el primer año y los ingresos promedio que
obtuvieron en el mismo periodo, como se muestra en la
gráfica de barras a la derecha. Calcule la utilidad prome
dio que lograron durante el primer año, restando los gas
tos promedio del primer año del ingreso promedio del
mismo periodo.
Reto
Gastos
($1,000)
Ingreso
($ 1,000)
40 30 20 10
-28
10 20 30 40 50 60
145. Realice esta operación: 1 - 2 + 3 - 4 + -- - + 9 9 ~ 100. (Sugerencia: Agrupe los números en parejas.)
146. Realice esta operación: 1 + 2 - 3 + 4 + 5 - 6 + 7 + 8 - 9 + 1 0 + 1 1 - 12 + ••• + 22 + 23 - 24. (Sugerencia: Exa
mine grupos de tres números.)
(1) • |—
2| •( —
3) •|4| •( —
5)
147. Realice esta operación: -— ¡------------ ¡— ¡--------¡— -. 148. Realice esta operación:
( l)( - 2 )( 3 ) (- 4 )( 5 ) -( 9 7 )( - 9 g )
( 1)(2)( 3)(4)( 5) - (—
97)(98) *
Ejercicios de repaso acumulativo
[1.2] 149. Responda verdadero o falso:Todos los números ra
cionales son números reales.
150. Liste el conjunto de los números naturales.
151. Considere el conjunto {3, 4, -2 , V 3 , o}. Liste
los elementos que son
a) números enteros,
b) números racionales,
c) números irracionales,
d) números reales.
152. A = {4,7,9,12}; B = {1, 4, 7,15}. Determine
a) i4 U 8 ,
b) A D B .
153. Ilustre {x| - 4 < x ^ 6} en una recta numérica.
I 1 .4 O R D E N D E L A S O P E R A C IO N E S
a
t
1 Calcular expresiones exponenciales.
2 Calcular raíces cuadradas y raíces de orden superior.
3 Calcular expresiones por m edio del orden de las operaciones.
4. Calcular expresiones que contengan variables.
5 Calcular expresiones con una calculadora graficadora.
A ntes d e estudiar el orden d e las operaciones, es necesario q u e hablem os brevem en
te acerca d e los exponentes y las raíces. Analizarem os m ás a fondo los exponentes en
las secciones 1.5 y 7.2.
1 C a lc u la r e x p re s io n e s e x p o n e n c ia le s
E n un problem a d e m ultiplicación, los núm eros o expresiones q u e se m ultiplican
reciben el nom bre d e factores. Si a-b = c,entonces a y b son factores d e c. Por ejemplo,
com o 2 - 3 = 6 , entonces 2 y 3 son factores d e 6. E l núm ero 1 es un factor d e todo
núm ero y expresión. ¿Puede explicar p o r qué?](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-57-320.jpg)



![Sección 1.4 • O rd e n d e las o p e ra cio n e s • 3 3
— C ó m o utilizar su ca lcu la d o ra
Cálculo de raíces co n una calculadora científica
Para determ inar las raíces cuadradas con una calculadora,se em plea la tecla correspondiente, [ V * [ . Para calcular V 25
en las calculadoras q u e tienen esta tecla, presione
i resu lta d o m o strad o
25 V * 5
Las raíces d e o rd en superior p u ed en determ inarse en calculadoras q u e tien en la tecla V y
Para calcular ^ 6 2 5 en una calculadora con la tecla V y , haga lo siguiente:
i resu lta d o m o strad o
o la tecla
625
Observe q u e el número que está dentro del signo radical (el radicando),625,se introduce prim ero, luego se presiona
la tecla ' ^ y y despuésse introduce la raíz (o índice),4. Cuando se presiona la tecla [ ^ ] aparece la respuesta: 5.
Para calcular ^625 en una calculadora con la tecla | y x ^utilice la tecla “inverso” com o sigue:
j resu lta d o m o strad o
625 ' IN V 0 4 0 5
•L a s tecjas p u e d e n v ariar e n c a d a c alcu la d o ra . A lg u n as tie n e n las teclas L i li o e n lugar d e la te c la [ ¿ J y o tra s tie n e n u n a tecla
o i sh ifl I e n lu g a r d e la tecla 1N V .
Cóm o utilizar su ca lcu la d o ra g ra fica d o ra
Cálculo de raíces con una calculadora graficadora
Para determ inar la raíz cuadrada en una calculadora graficadora, use V - . Por lo general, el sím bolo V - aparece
arriba d e la tecla | x 2 , así q u e usted tendrá q u e presionar la tecla 121
*11p ara calcular raíces cuadradas. Por ejem
plo, p ara calcular V 5 5 presione
[2a ] [ x* 25 1E N T E R 5 <
----- resultado mostrado
O tando presiona [2nd] | x 2 , la calculadora Texas Instrum ents T I-8 3 Plus genera V - (. Luego usted inserta el ra
dicando y presiona E N T E R . para aprender a calcular raíces cúbicas y d e orden superior, consulte el m anual
de su calculadora graficadora. C on la T I-8 3 Plus, puede usar la tecla
varias opciones, incluyendo la 4 y la 5, q u e se m uestran a continuación.
4: V ~( 5
M A TH . O tando la presione obtendrá
La opción 4 puede usarse p ara calcular raíces cúbicas, y la opción 5 p ara determ inar raíces d e orden superior, co
mo se m uestra en los siguientes ejemplos.
E J E M P L O
Solución
Calcule: ^ 1 2 0 .
M A TH 4 120
s e le c c io n é in tro d u zca
la o p c ió n 4 e l rad ican d o
E N T E R
l----------
4.932424149
resu lta d o m o strad o
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-61-320.jpg)
![3 4 • Capítulo 1 • C o n c e p to s básicos
Para determ inar una raízcon un índice m ayor q u e 3,prim ero introduzca el índice, luego presione la tecla
y después la opción 5.
M A TH
E J E M P L O Calcule: ^ 6 2 5 .
S o lu c ió n
índice
/
M A TH 5 625
* >
— —
sele c c io n e 7 in tro d u zca
la o p c ió n e l rad ican d o
E N T E R
resu lta d o m o strad o
Cuando estudiem os los exponentes racionales en la sección 7.2, m ostrarem os o tra form a d e determ inar raí
ces e n una calculadora graficadora.
AHOR A RESUELVA EL EJERCICIO 37
3 C a lc u la r e x p re s io n e s p o r m e d io d el o rd e n d e las o p e ra c io n e s
M uchas veces usted tendrá q u e calcular expresiones q u e contienen varias operaciones.
Para hacerlo, siga el orden de las operaciones que se indica a continuación.
O rd e n d e las o p e ra c io n e s
Para calcular expresiones matemáticas, utilice este orden:
1. Primero calcule las expresiones que están dentro de símbolos de agrupación, in
cluyendo los paréntesis ( ), los corchetes [ ],y las llaves { }. Si la expresión con
tiene símbolos de agrupación anidados (una par de símbolos de agrupación
dentro de otro), calcule primero las expresiones que están dentro de los símbolos
de agrupación más internos.
2. Después calcule todos los términos que tengan exponentes y raíces.
3. A continuación realice todas las multiplicaciones y divisiones, en el orden en que
aparezcan, trabajando de izquierda a derecha.
4 Pbr último, realice todas las sumas y restas en el orden en que aparezcan, traba
jando de izquierda a derecha.
Es necesario aclarar q u e la barra de fracción actúa com o un símbolo d e agrupación. Por
lo tanto, cuando se calculan expresiones q u e contienen una barra d e fracción, se tra
baja d e form a separada arriba y abajo de la misma.
Los corchetes se usan con frecuencia en lugar d e paréntesis p ara evitar confusio
nes. Por ejem plo, la expresión 7((5 • 3 ) + 6 ) es más fácil d e seguir cuando se escribe
7[(5 • 3) + 6]. R ecuerde calcular prim ero el grupo más interno.
E J E M P L O 7 C alcule8 + 3 • 52 - 7.
Solución U sarem os un som breado p ara indicar el orden en el q u e se realizan las operaciones.
Com o en esta expresión no hay paréntesis, prim ero calculam os 52.
8 + 3 - 5 2 - 7 = 8 + 3 - S 2 - 7
D espués realizam os las multiplicaciones y divisiones d e izquierda a derecha.
= 8 + 75-7
Por últim o, realizam os las sum as y restas d e izquierda a derecha.
= 8 3 - 7
= 76 #](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-62-320.jpg)
![Sección 1.4 • O rd e n d e las o p e ra cio n e s • 3 5
E J E M P L O 8 Calcule: 10 + {6 - [4(5 - 2)]}2.
S o l u c i ó n Prim ero, trabaje con la expresión q u e está dentro d e los paréntesis más internos. C on
tinúe d e acuerdo con el orden d e las operaciones.
10 + {6 - [4(5 - 2)]}2 = 10 + {6 - [4(3)]}2
= 10 + [6 - (12)]2
= 10 + (-6 )2
= 10 + 36
AHOR A RESUELVA EL EJER CICIO 7 7 = 46 #
E J E M P L O 9 Calcule: 1 + ^ ^
S o l UCÍÓn R ecuerde q u e la barra d e fracción actúa com o un sím bolo d e agrupación. T rabaje de
m anera separada las operaciones q u e están arriba y abajo d e la barra d e fracción.
6 + + 5|7 —3| 6 f | + 5|4|
l + ( 3 - 5 ) + 2 ” l + (-2 ) + 2
12 + 20
" 1 + ( - 1 )
= —
0
Com o la división entre cero no es posible, la expresión original no está definida. #
4- E v a lu a r e x p re s io n e s q u e c o n te n g a n v a ria b le s
Para evaluar expresiones m atem áticas usamos el orden d e las operaciones q u e acaba
d e explicar. E l ejem plo 10 es un problem a d e aplicación en el q u e lo hacemos.
E J E M P L O 1 O R em edios alternativos La frustración q u e en ocasiones provoca la m edicina con
vencional ha llevado a m uchos estadounidenses a intentar rem edios alternativos, tales
com o vitam inas, hierbas y o tro s com plem entos disponibles sin la prescripción del
doctor. Las ventas aproxim adas d e tales com plem entos entre 1995 y 2002, en miles de
m illones d e dólares, puede calcularse p o r medio d e la ecuación
ventas = -0.063a
:2 + 1.62a
: + 9.5
en donde x representa los años desde 1995. E n la expresión q u e está a la derecha del
signo de igualdad, sustituya x por 1 p ara calcular las ventas d e com plem entos en 1996,
x p o r 2 p ara estim ar las ventas d e com plem entos en 1997, y así sucesivamente.
Calcule las ventas d e com plem entos durante a) 1996 y b) 2000.
S o l u c i ó n a ) Sustituirem os x por 1 p ara estim ar las ventas d e com plem entos en
1996.
ventas = -0.063.*2 + 1.62a: + 9.5
= -0.063(1)2 + 1.62(1) + 9.5
= -0.063 + 1.62 + 9.5
= 11.057
Por lo tanto, en 1996 se vendieron com plem entos con un valor d e alrededor d e $11.057
miles d e millones en Estados Unidos.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-63-320.jpg)

![Sección 1.4 • O rd e n de las o p e ra cio n e s • 3 7
E N T E R , aparecerá
diferente d e la variable. L ea el m anual d e su calculadora graficadora p ara aprender
cómo realizar cálculos con una expresión p ara diferentes valores d e la variable sin tener
q u e reintroducirla cada vez. E n la T I- 8 3 Plus, después de calcular una expresión p ara
un valor d e la variable,puede presionar | 2 nd 11 E N T E R | para desplegar el valor asig
nado previam ente y la expresión a calcular. D espués puede reem plazar el valor q u e fue
asignado a X con el nuevo valor. Luego d e hacerlo y presionar
la nueva respuesta.
La pantalla d e la calculadora q u e se m uestra en la figura 1.9 ilustra dos puntos
im portantes respecto d e las calculadoras graficadoras.
L O bserve los paréntesis alrededor d e 2/3. Algunas calculadoras graficadoras inter
pretan 2/Z3*2 com o 2/(3*2). Para calcular §*2 en ellas, deb e usar paréntesis alre
d ed o r d e 2/3. E s necesario q u e aprenda cóm o trab aja su calculadora con
expresiones tales com o 2/3X2. Siempre que tenga duda, utilice paréntesis para pre
venir posibles errores.
2. E n la pantalla observará q u e el signo negativo q u e precede a 2.3 es ligeram ente
m enor y está m ás arriba q u e el signo d e resta q u e antecede al núm ero 4 en la
expresión. Por lo regular, las calculadoras graficadoras tienen una tecla d e signo ne
gativo, ( ~ ) , y o tra p ara el signo d e sustracción, D eb e estar seguro de
utilizar la tecla correcta u ob ten d rá un resultado erróneo. L a tecla del signo nega
tivo se usa p ara introducir un número negativo. L a tecla d e sustracción se em plea
p ara restar una cantidad d e o tra. Para introducir la expresión - x - 4 en una
calculadora gráfica, podría presionar
E JE M P L O 12
3+X:0.71X2+2.16X
+145.39
158.26
8+X:0.71X2+2.16X
+145.39
208.11
F IG U R A 1.10
Solución
H l | x , T , 0 , n | P 1 4
T
signo
negativo
T
resta
R ecuerde q u e - x - 4 significa - l x - 4. Al iniciar con [ ( ~ ) [ usted introduce el coe
ficiente - 1 . D iferentes calculadoras usan teclas distintas p ara introducir la variable x.
La tecla que se muestra después del signo negativo, es la q u e se utiliza en la calculadora
T I-8 3 Plus.
Precio prom edio de venta de viviendas Tasas bajas d e interés, facilidad p ara obtener
créditos y una fuerte dem anda d e la clase m edia mantuvieron bajo control el precio p ro
m edio d e venta d e las viviendas en Estados U nidos en tre 1992 y 2001. E l precio p ro
medio d e una casa,en miles d e dólares,durante ese periodo puede estim arse m ediante
esta ecuación:
precio prom edio d e venta = 0.71*2 + 2.16* + 145.39
en donde * representa los años desde 1992. E n la expresión q u e está a la derecha del
signo igual, sustituya * por 1 p ara calcular el precio prom edio d e venta d e una casa en
1993,* por 2 para calcular el precio prom edio d e venta en 1994, y así sucesivamente.
Si cuenta con ella, utilice una calculadora graficadora para calcular el precio prom edio
d e venta d e una casa en a) 1995 y b) 2000. Fuente: Asociación Nacional d e C orredo
res d e Bienes Raíces (de Estados Unidos).
a) Al año 1995 le corresponde el valor * = 3, d e m odo q u e com ience p o r asignar a*
un valor d e 3; luego introduzca la expresión y presione | E N T E R ]. E n la figura 1.10
se m uestra la pantalla de una calculadora T I -8 3 Plus con el cálculo p ara expresión
cuando el valor es * = 3. Com o puede ver, el precio prom edio d e venta d e una casa en
1995 fue de aproxim adam ente 158.26 miles d e dólares, es decir, $158,260.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-65-320.jpg)
![3 8 • C apítulo 1 • C o n c e p to s básicos
b) Como 2000 - 1992 = 8, al año 2000 le corresponde el valor x = 8. A signe prim ero
a x un valor d e 8 ; después vuelva a introducir la expresión y presione E N T E R
Com o puede ver en la figura 1.10,el precio prom edio d e venta d e una casa en 2000 fue
d e aproxim adam ente 208.11 miles d e dólares, es decir, $208,110. #
SU G ERENCIA Siem pre revise la pantalla d e su calculadora p ara asegurarse d e q u e no presionó
alguna tecla p o r error ni om itió algún dato. O bserve q u e no es necesario introdu
cir el 0 antes del punto decim al en térm inos com o - O J lx 2.
C o n j u n t o d e e j e r c i c i o s 1.4
Ejercicios conceptuales
h C b n s id e re la e x p r e s ió n an y re s p o n d a :
a) ¿ C ó m o s e d e n o m in a a e n e s ta e x p re s ió n ?
b) ¿ C ó m o s e d e n o m in a ni
2 . ¿ C u á l e s e l s ig n ific a d o d e a ” ?
3 . C b n s id e re la e x p r e s ió n ra d ic a l /a .
a) ¿ C ó m o s e d e n o m in a n e n e s ta e x p re s ió n ?
b) ¿ C ó m o s e d e n o m in a a?
4 . S i = b, ¿ q u é sig n ific a ?
5 . ¿ C u á l e s la ra íz c u a d r a d a p rin c ip a l d e u n n ú m e ro p o sitiv o ?
6 . E x p liq u e p o r q u é V ^ 4 n o p u e d e s e r u n n ú m e ro re a l.
7 . E x p liq u e p o r q u é u n a ra íz im p a r d e u n n ú m e ro n e g a tiv o
s e r á n e g a tiv a .
8 . E x p liq u e p o r q u é u n a ra íz im p a r d e u n n ú m e ro p o sitiv o s e
rá p o s itiv a .
9. Explique con sus propias palabras el orden de las opera-
dones que se debe seguir cuando se evalúa una expresión
matemática.
10. a) Explique con sus propias palabras y paso a paso cómo
calcularía la siguiente expresión
5 - 18 -s- 32
4 - 3-2
b) Realice los cálculos y dé el resultado de la expresión
anterior.
11. a) Explique con sus propias palabras y paso a paso cómo
calcularía 16 -s- 22 + 6 •4 - 24 h- 6.
b) Realice los cálculos y dé el resultado de la expresión
anterior.
12. a) Explique con sus propias palabras y paso a paso cómo
calcularía {5 - [4 - (3 - 8)]}2.
b) Realice los cálculos y dé el resultado de la expresión
anterior.
Problemas de aplicación
Resuelva cada expresión sin utilizar una calculadora.
13. 32 14. ( - 4 ) 3 15. - 3 2 16.
17. ( -3 )2
- ( I T » • - ( ! T
20.
2L
- ( - ! ) ’
22. V I44 23. -V 3 6 24.
25.
3/-216
*■ V 343
27. ^0.001 28.
—
43
(0.3)2
V ^64
T
Utilice una calculadorapara resolver cada expresión. Redondee las respuestas al milésimo más cercano.
29. (0.35)4 30. -(1 .7 )3-9 31. 32.
33. (6.721)5.9
34. V92 35. ^ 5 36. - < / ñ J
15](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-66-320.jpg)
![Calcule a) x2y b) - x 2para cada valor dado de x
4L 3 42. 4 43. 1 44. -2
45. -1 46. - 5 & 47. | 48. - |
Calcule a) x*y b) -x 3para cada valor dado de x.
49. 3 50. - 5 51. - 3 5Z -1
Sección 1.4 • O rd e n d e las o p e ra cio n e s • 3 9
Calcule cada expresión.
57. 32 + 23 - 22 - 33 58. ( -1 )2 + ( - 1 ) 3 - l4 + l5 £ 59. - 2 2 - 23 + l10 + ( - 2 ) 3
60. ( - 3 ) 3 - 22- ( - 2 ) 2+ (4 - 4)2 6L (1.5)2 - (3.9)2 + (-2 .1 )3 61 (3.7)2 - (0.8)2 + (2.4)3
“ g H -B J +íf
Calcule cada expresión.
65. 2 + 5-8 66. (2 - 7 ) + 5 + 1 67. 1 8 - 6 + 6 + 5
68. 4*3 -s- 6 - 2 2 69.
3
— —
4
i - 2 + 2 + 4
2
70. 3 -4 - 1 2 + |
7L
1 . 2 . 3 _ 1 / 1
2 3 4 6 V 3 /
72. 3[4 + (-2 )(8 )] + 33 73. 10 + [(3 + 22) - (24 - 8)]
74 [3 - (4 - 23)2]2 75. 5 (^ T ¡ + ^ 1 6 ) : V J°° 76. {3 + [42 - 3(2 - 7)] - 3 )2
77. {[(12 - 15) - 3] - 2}2 78. 3{6 - [ ( 2 5 + 5) - 2]}3 79. 4(5(13 - 3) + (25 + 5)2]2
80.
15 + 3 + 2 -2 ^
81.
4 - (2 + 3)2 - 6 2 (—
3) + 4 -5 - 32
V 25 + 5 + 8 + 2 4(3 - 2) 32 824 - 6 + V5(22 - 1)
83.
8 + 4 r 2 - 3 + 4
84.
- i
+ 4
8 - [4 - (3 - l ) 2]
52 - 32•2 - 7
z
5 - ( -3 )2 + 4 + 2
86. 12 - 15 -i- |5| - (|4| - 2)2 87. "2 - 3 | - V 36 + |2| + 32
4 - |—
12| + |3|
2 ( 4 - |5 |) + 9
89.
6 - |-4 | - 4|6 - 3|
90. - i [ 8 - |-6 | + 3 - 4]2
5 - 6*2 -i- |-6 |
91. |[ > f é 7 - |- 9 | + 4 - 3 2]2
3(5 -
o?
2)2 2(32 - 42)
^ - 3 4 - (-2 )
93.
24 - 5 - 42 4 - ( - 3 ) 2 + 4| - 2 - 8 + 4 ! -18| [(8 - 3)2 - 4]2
|-8 | + 4 - 2 ( 3 ) 32 - 4*3 + |--7| 94 |8| - VB4 ' 22 + 16
Calcule cada expresión para el valor o valores dados.
95. 5*2 + 3* cuando x = 2 96. 5*2 - 2x + 5 cuando x = 3
97. -9 * 2 + 3* - 29 cuandox = - 1 98. 3(* - 2)2cuando* = j
99. 16(* + 4)3 - 25(* + 4) cuando* = - 3 100. -6 * + 3 / cuando * = 2, y = 4
101. 6*2 + 3y3 - 5 cuando * = 1, y = - 3 102. 4*2 - 3y - 5 cuando * = 4, y = - 2](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-67-320.jpg)
![4 0 • Capítulo 1 • C o n c e p to s básicos
S 103. 3(a + b)2 + 4(a + b) - 6 cuando a = 4, b = -1
105. - 6 - {* - [2* - (x - 3)]} cuando* = 4
- b + V b 2 - 4ac
107.
2a
cuando a = 6 ,b = -11, c = 3
104. - 3 - [2x ~ [5* - (2* + 1)]} cuando* = 3
(* - 3f (y + 5)2
106. ---- + ------77---- cuando * = 4, y = 3
108.
9 16
- b - Vfr2 ~ 4ac
2a
cuando a = 2, b = 1, c = -1 0
Resolución de problemas
En los ejercicios 109 a 113, escriba una expresión algebraicapara cada problema* Luego calcule la expresiónpara el valor dado de la
variable o variables.
109. Multiplique la variable y por 7. Del producto que obtenga
reste 14.Ahora divida esta diferencia entre 2. Determine
el valor de esta expresión cuando y = 6.
110. Reste 4 de z .Multiplique esta diferencia por 5. Ahora ele
ve al cuadrado el producto. Determine el valor de esta ex
presión cuando z = 10.
í ~ 111. Sesuma 6 al producto de 3 y *. Esta expresiónse multiplica
después por 6. Luego se resta 9 del producto. Determine
el valor de la expresión cuando * = 3.
0 Utilice una calculadorapara responder los ejercicios 114 a 121.
114. Centenarios A las personas que viven 100 años o más se
lesconoce como centenarios. De acuerdo con la Oficina de
Cénsos de Estados Unidos, los centenarios conforman el
grupo de edad que crece más rápido en el mundo. El nú
mero aproximado de centenarios que viven o vivirán en
Estados Unidos entre los años 1995 y 2050,en miles, pue
de estimarse mediante la ecuación
número de centenarios = 0.30*2 - 3.69* + 92.04
en donde * representa los años desde 1995. Sustituya * por
1 para determinar el número de centenarios que había en
1996,* por 2 para encontrarel número de centenarios que
había en 1997,y así sucesivamente.
a) Estime el número de centenarios que vivían en Estados
Unidos en 2000.
b) Estime el número de centenarios que vivirán en Esta
dos Unidos en 2050.
Fuente:Oficina de Censos de Estados Unidos.
115. Transportepúblico El aumento en el precio de la gasolina
y el creciente problema de congestionamientos de tránsito
en lasprincipales ciudades de Estados Unidos han provoca-
cb queel transporte público se utilicecada vez más Para cal
cular el número aproximado de viajesen transporte público
realizadoscada añoentre 1992y 2001 en Estados Unidos,en
milesde millones, puede calcularse usando la ecuación
número de viajes = 0.065*2 - 0.39* + 8.47
en donde * representa los años desde 1992.Sustituya * por
1 para calcular el número de viajes realizados en 1993, *
par 2 para calcular el número de viajes hechos en 1994,y
asísucesivamente.
a) Calcule el número de viajes realizados en transporte
público en 2000.
b) Suponga que la tendencia de aumento continúa. Calcu
le el número de viajes que se realizarán en 2010.
Fuente: Asociación Estadounidense de Transporte
Público.
112. La suma de * y y se multiplica por 2. Después se resta 5 de
este producto. Luego, esta expresiónse eleva al cuadrado.
Determine el valor de la expresión cuando * = 2 y y =
-3.
113. Se suma 3 a *. El resultado se divide entre el doble de y.
Luego, el cociente resultante se eleva al cuadrado. Por úl
timo,se resta 3 de esta expresión. Determine el valor de la
expresión cuando * = 5 y y = 2.
116. Dióxido de carbono Desde 1905, la cantidad de dióxido
de carbono (C 02) presente en la atmósfera terrestre ha
ido aumentando. La producción total de C 02de todos los
países, excepto Estados Unidos, Canadá y las naciones de
Europa Occidental (medida en millones de toneladas mé
tricas) puede calcularse mediante la ecuación
C02 = 0.073*2 - 0.39* + 0.55
endonde * representa cada periodo de 10 años desde 1905.
Sustituya * por 1 para calcular la producción de C 0 2en
1915,* por 2 para calcular la producción de C 0 2en 1925,
* por 3 para calcularla en 1935,etcétera.
a) Determine la cantidad aproximada de CO?producida
por todos los países (excepto Estados Unidos, Canadá
y las naciones de Europa Occidental), en 1945.
b) Suponga que esta tendencia de aumento continúa; de
termine la cantidad aproximada de C 0 2producida por
todos los pafces (excepto Estados Unidos, Canadá y las
naciones de Europa Occidental) a i 2005.
Véase el ejercicio 115](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-68-320.jpg)
![Sección 1.4 • O rd e n d e las o p e ra cio n e s • 4 1
bu 117. Niños auíosuficientes El número de niños autosuficien-
tes, es decir, niños que se cuidan solos mientras sus padres
trabajan, aumenta en relación directa con la edad. El por
centaje de niños de edades diferentes, de 5 a 14 años,que
son autosuficientes puede calcularse mediante la ecuación
porcentaje de niños = 0.23*2 - 1.98* + 4.42.
El valor de x representa la edad de los niños. Por ejemplo,
sustituya x por 5 para obtener el porcentaje de todos los
niños autosuficientes de 5 años;sustituya x por 6 para ob
tener el porcentaje de todos los niños autosuficientes de 6
años, etcétera.
a) Determine el porcentaje de todos los niños autosufi-
cientes de 10 años.
b) Determine el porcentaje de todos los niños autosufi
cientes de 14 años.
118. Lectoresdeperiódicos El número de estadounidenses que
acostumbran leer periódicos va constantemente a la baja.
El porcentaje de lectores de periódicos puede calcularse
mediante la ecuación
porcentaje = - 6.2* + 82.2
en donde * representa cada periodo de 10 años desde 1960.
Sustituya * por 1para obtenerel porcentaje para 1970;pa
ra 1980sustituya * por 2;sustituya * por 3 para obtener el
porcentaje para 1990,etcétera.
a) Determine el porcentaje de estadounidenses adultos
que leían periódicos en 1970.
b) Suponiendo que esta tendencia a la baja continúe, de
termine el porcentaje de estadounidenses adultos que
leerán periódicos en 2010.
119. Cultivos orgánicos El aumento del temor que provoca
el uso de pesticidas y la manipulación genética de las co
sechas, ha ocasionado que las personas tiendan cada vez
más acomprar alimentos cultivados de manera orgánica.
Ejercicios de repaso acumulativo
[1.2] 122. A = [a, b, c, d,f , B = Determine
a) A H B,
b) A U B.
[1.3] En los ejercicios123 a 125, la letra a representa un número
real. ¿Paraqué valores de a será verdaderacada afirmación?
123. U = |-fl|
Entre 1990 y 2001, las ventas,en miles de millones de dó
lares, de alimentos cultivados de manera orgánica puede
calcularse por medio de la ecuación
ventas = 0 .062*2 + 0.020* + 1.18
en donde * representa los años desde 1990.Sustituya * por
1para calcular las ventas de alimentos cultivados de ma
nera orgánica en 1991, sustituya * por 2 para estimar las
ventas en 1992,y asísucesivamente.
a) Calcule las ventas de este tipo de alimentos en 1991.
b) Calcule las ventas de este tipo de alimentos en 2001.
120. Afiliación asindicatos El número de trabajadores sindica-
izados ha estadocambiando en Estados Unidos. Entre 1983
y2001, la afiliación, considerada como un porcentaje de la
fueiza laboral total,puede calcularse usando la ecuación
porcentaje de trabajadores sindicalizados =
0.016*2 - 0.62* + 19.69
en donde * representa los años desde 1983.Sustituya * por
1 para calcular el número de trabajadores sindicalizados
como un porcentaje de la fuerza laboral total en 1984, *
por 2 para estimar el porcentaje en 1985,etcétera.
a) Calcule el número de trabajadores sindicalizados como
un porcentaje de la fuerza laboral total en 1991.
b) Calcule el número de trabajadores sindicalizados co
mo un porcentaje de la fuerza laboral total en 2001.
Fuente: Oficina de Estadísticas Laborales de Estados
Unidos.
121. Teléfonoscelulares El uso de teléfonos celulares está au
mentando en la actualidad. El número de usuarios de ce
lulares,en millones, puede calcularse mediante la ecuación
número de usuarios = 0.42*2 - 3.44* + 5.80
en donde * representa los añosdesde 1982.Sustituya* por 1
para obtener el número de usuarios en 1983,* por2 para ob
tener el número de usuarios en 1984,y asísucesivamente.
a) Determine el número de usuarios de teléfonos celula
res en 1989.
b) Determine el número de usuarios de teléfonos celula
res en 2002.
124 |a| = a
125. a = 4
126. Liste de menor a mayor: —16|, -4 , |-5 |, - |- 2 |,0 .
127. Señale el nombre de esta propiedad: (2 + 3) + 5 =
2 + (3 + 5).](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-69-320.jpg)










![Reto
5 2 • Capítulo 1 • C o n c e p to s básicos
En la sección 7.2 aprenderá que las reglas de los exponentes que acabamos de presentar, también se aplican cuando los exponentes
son números racionales. Con base en esta información y en las reglas délos exponentes, resuelva cada expresión.
( *
4Y
b ) 139.
b J
x w y - w / , v y V
*5^5/3 142.
UV'V
Actividad en equipo_____________
Analice y responda en equipo el ejercicio 143.
143. Centavos que crecen El día 1 se le da un centavo. Cada
m o de los días que siguen se le dará el doble de la canti
dad que se le entregó el día anterior.
a) Escriba lascantidades que le darían en cada uno de los
primeros 6 días.
b) Señale cada uno de estos números como una expresión
exponencial con una base de 2.
c) Buscando un patrón, determine una expresión expo
nencial para el número de centavos que recibirá el
día 10.
Ejercicios de repaso acumulativo
d) Escriba una expresión exponencial general para el nú
mero de centavos que recibirá el día n.
e) Escriba una expresión exponencial para el número de
centavos que recibirá el día 30.
f) Calcule el valor de la expresión en la parte e). Si tiene
calculadora, utilícela.
g) Determine la cantidad, en pesos, que obtuvo como re
sultado en la parte f).
h) Escriba una expresión exponencial general para el nú
mero de pesos que recibirá en el día n.
[1.2] 144. Si A ={3, 4, 6} y B = {1, 2, 5, 8}, determine [1.4] 146. Calcule: 6 + |l2| -r |- 3 | - 4 -2 2.
a M U B y h M n * . 147.Evalúale '3/-T2S.
145. Ilustre el siguiente conjunto en la recta numérica:
{*1-3 < * < 2}.
1 .6 N O T A C I Ó N C IE N T IF IC A
f l ¡Sé
1 Escribir núm eros en notación científica.
2 Cam biar núm eros en notación científica a form a decimal.
3 Usar notación científica en la resolución de problemas.
1 E s c rib ir n ú m e ro s e n n o ta c ió n cien tífica
C on m ucha frecuencia, los científicos e ingenieros tienen q u e trabajar con núm eros
muy grandes y muy pequeños. Por ejem plo, la frecuencia d e la señal d e un radio FM
puede ser d e 14,200,000,000 hertz (o ciclos p o r segundo), y el diám etro d e un átom o
d e hidrógeno es de alrededor d e 0.0000000001 metros. D ebido a la dificultad q u e im
plica trabajar con m uchos ceros, a m enudo los científicos expresan tales núm eros con
exponentes. Por ejem plo, el núm ero 14,200,000,000 podría escribirse com o 1.42 X 1010
y 0.0000000001 com o 1 X 10~10. Esta representación abreviada se conoce com o notación
científica. E n notación científica, los núm eros aparecen com o un número m ayor o igual
a 1 y m enor q u e 10, m ultiplicado p o r alguna potencia d e 10. E l exponente d e 10 d e
be ser un entero. C uando una potencia d e 10 no tiene coeficiente num érico, com o](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-80-320.jpg)


![5 6 • Capítulo 1 • C o n c e p to s básicos
Así, alrededor d e $1.94256 X 1011 o $194,256,000,000 fueron recaudados a partir de
los ingresos personales m ediante im puestos en 2000.
b) En 1970 se recaudó $4,800 X 1010en impuestos. E n 2000 se recaudaron $5.396 X 1011
p o r el mismo concepto. Para determ inar la diferencia en estas cantidades, restarem os
el m onto recaudado en 1970 del recaudado e n 2000. Escribim os 4.800 X 1010com o
480 X 1010y restam os com o sigue:
d iferencia e n im puestos recaudados = 5.396 X 1 0 " - 4.80 x 1010
= 53.96 X 1010 - 4.80 X 1010
= (53.% - 4.80) X 1010
= 49.16 X 1010
= 4.916 X 1 0 "
Por lo tan to , $4.916 X 1011 o $491,600,000,000 m ás fu ero n recaudados e n 2000 q u e
e n 1970.
c) Para determ inar el número de veces que fue m ayor la cantidad recaudada en 2000
q u e en 1970, dividimos com o sigue:
n ú m ero d e veces m ayor = -
m onto recaudado en 2000
m onto recaudado en 1970
5.396 x 101
1
4.80 X 1010
5 3 9 6 -MI_10
4.80 * 10
« 1.1242 X 10*
Así, la cantidad recaudada en 2000 fue alrededor d e 1.1242 X 101u 11.242 veces m a
yor q u e la cantidad recaudada en 1970.
d) A partir d e los resultados obtenidos en las partes b) y c), sabem os q u e se recaudó
una cantidad d e im puestos m uy superior en 2000 q u e en 1970. Las gráficas m uestran
que un porcentaje más pequeño en 2000 proviene d e los im puestos sobre las ventas
(47% contra 57% ),y un porcentaje más grande proviene del impuesto sobre el ingre
so personal (36% contra 19% ). Tam bién hay cam bios m enores en los porcentajes de
los otros sectores. #
3.2E12. En ambos casos se representa 3.2 X 1012,que es igual a 3,200,000,000,000.
Para introducir números en notación científica en una calculadora científica o en una calculadora graficadora, por
b común se utilizan las teclas E E E X P E E ,o bien, 4.6. La pan-
. Para introducir 4.6 X 10®,se debe presionar 4.6
talla de su calculadora podría mostrar 4.6 °8, o bien,4.6E8.
En la T I-8 3 Plus, la leyenda EE aparece debajo de la tecla [T . Por lo tanto, para introducir (8,000,000)(400,000)
en notación científica presionaría
8 J ^ j ] [7]6 [ x ] 4 T|5 E N T E R
r resultado mostrado
3.2E12
para activar EE para activar EE](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-84-320.jpg)



![Reto
6 0 • Capítulo 1 • C o n c e p to s básicos
79. Ano luz Un año luz es la distancia que recorre la luz du
rante 1 año solar.
a) Determine el número de millas en un año luz,si la luz
viaja a 3 X 105kilómetros por segundo.
b) SlaTierra está alejada del Sol por 150,000,000 kilóme
tros, ¿cuánto tarda la luzdel Sol en llegar a la Tierra?
c) Nuestra galaxia, la Vía Láctea, tiene una longitud de
casi 1 X 1017kilómetros. Si una nave espacial viajase a
la mitad de la velocidad de la luz, ¿cuánto tardaría en
ir de un extremo a otro de la galaxia?
R e s u m e n d e l c a p i t u l o
Términos y frases importantes
1.2
C onstante
Núm eros p ara contar
Elementos de un conjunto
Puntos extrem os
Expresión
D esigualdades
Enteros
Intersección de conjuntos
Núm eros irracionales
Núm eros naturales
Conjunto vacío (o nulo)
O peraciones
Núm eros racionales
N úm eros reales
Form a d e lista
Conjunto
N otación d e construcción
d e conjuntos
Subconjunto
U nión d e conjuntos
Variable
E nteros no negativos
1 .3
Valor absoluto
Idéntico aditivo
Inverso aditivo
Propiedades asociativas
Propiedades conmutativas
Propiedad distributiva
Idéntico multiplicativo
Inverso multiplicativo
O puestos
Propiedades d e los núm e
ros reales
Recíproco
1 . 4
Base
Exponente
Expresión exponencial
Factor
Calculadora graficadora
Indice
O rden d e las operaciones
R aíz cuadrada principal
Signo radical
Radicando
Expresión indefinida
1.6
N otación científica
H e c h o s i m p o r t a n t e s
Conjuntos de núm eros
Núm eros reales
Núm eros naturales o p ara contar
Núm eros enteros no negativos
Enteros
Núm eros racionales
Núm eros irracionales
{*|* es un p u n to d e la recta num érica}
{1,2, 3 ,4 ,5 ,...}
{0,1,2, 3,4,...}
{ . . . , - 3 , - 2 , - 1 , 0 , 1 , 2 , 3, ...}
p y q so n en tero s, q * 0
{*1* es un núm ero real q u e no es racional}
Desigualdades en la recta d e los n úm e ros reales
{ x x > a } ^_____j*
{ x x < a )
{xa < x < b]
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-88-320.jpg)

![Ejercicios de repaso del capítulo
6 2 • Capítulo 1 • C o n c e p to s básicos
[1.2] Exprese cada conjunto en forma de lista.
L A = {x|* es un número natural entre 3 y 8}. 2. B = {*|* es un entero no negativo múltiplo de 3}.
Sea N = conjunto de los números naturales, W = conjunto de los enteros no negativos, Z = conjunto de los enteros, Q = conjunto de
números racionales, I = conjunto de números irracionales, y R = conjunto de números reales. Determine si el primer conjunto es un
subconjunto del segundo conjunto para cada pareja.
3. N ,W 4. Q, 5. /, 6. Q J
Considere el conjunto de números {-2, 4,6, V f , V 3 ,0, ¿f, - j, 1.47}. Usté los elementos del conjunto que son:
7. números naturales. 8. enteros no negativos. 9. enteros.
10. números racionales. 11. números irracionales. 12 números reales.
Indique si cada afirmación es verdadera o falsa.
13. y no es un número real.
15. Un número real no puede dividirse entre cero.
Determine A U B y A D B para cada conjunto A y B.
17. A = {X 2, 3, 4,5, 6}, B = {2, 4, 6, 8,10}
19. A = {1,3, 5, 7, ...} ,« = {2, 4, 6, 8, ...}
Ilustre cada conjunto en la recta numérica.
2L {*|* > 5} 2 2 {xx ^ -2 }
14. 0, | , -2 , y 4 son números racionales.
16. Todos los números racionales y todos los números irracio
nales son números reales.
18. A = {3, 5,7, 9}, 8 = {2,4, 6, 8}
20. A = {4,6,9,10,11 },B = {3,5, 9,10,12}
23. {jr|—
1.3 < x £ 2.4} 24 j.v j S * < 4 y xeA /)
[1.3] Escriba < , > o = en el área sombreada entre los dos números para que cada afirmación sea verdadera.
25. - 8 B 0
29. |-4 | ■ |-6 |
26. - 4 ■ -3.9
30. 13 ■ - 5
27. 1.06 « 1 .6
31.
28. |-3 | ■ 3
3 2 —|—
2| ■ -5
Ordene los números de cada lista de menor a mayor.
33. 7 7 , - 7 7 , - 3 , 3
35. |- 7 |, |-5 |,3 , - 2
37. -4 , 6, —
| —
3|, 5
Mencione el nombre de cada una de las siguientes propiedades.
39. - l ( x + 4) = - I x - 28
4L (x + 3) + 2 = * + (3 + 2)
43. 5(rs) = (5r)s
45. 5(0) = 0
34 0 ,|,2 .3 ,|- 3 |
36. |- 3 |, - 7 , |- 7 |, - 3
38. |1.6|, |-2 .3 |, - 3 ,0
40. m n = nm
42 q + 0 = 0
44. - ( - 5 ) = 5
46. a + (~a) = 0
47. = 1
x
48. * + / = !• (* + /)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-90-320.jpg)
![Ejercicios d e re p a so del capítulo • 6 3
[1.3, 1.4] Resuelva las siguientes expresiones.
49. 7 + 32 - V36 + 2
52. 2 |-7 | - 4 |-6 | + 3
55. + ^ 6 4 + </Í6
58. 52 + ( - 2 + 22)3 + l4
5+ 7-4- (32 - 2 ) + 4 - l
6L
50. - 4 -r ( - 2 ) + 16 - V49
53. (6 - 9) + (9 - 6) + 1
56. 32 - 6 •9 + 4 -i- 22 - 3
59. - 3 2 + 14 + 2 -3 - 6
- ( 4 - 6)2 - 3(—
2) + |-6 |
5L (4 - 6) - ( - 3 + 5) + 12
54 | 6 - 3 | + 3 + 4 - 8 - 1 2
57. 4 - (2 - 9)° + 32 + 1 + 3
60. {[(9 + 3)2 - l] 2 + 8}3
V Sl + V I - 10
62.
1 8 -9 -4 - 3-5
63. Resuelva Ix2 + 3x + 1 cuando x = 2.
64 Resuelva 5o2 - Ib2cuando a = - 3 y b = —
4—
65. Campaña política El costo de las campañas políticas ha
cambiado de formadramática desde 1952.El monto gastado,
en millones de dólares, en todas las elecciones de Estados
Unidos,incluyendo elecciones municipales,estatales y de mi
nisterios nacionales, partidos políticos,comitésde acciónpo
lítica y papelería para la votación, se puede calcular por
medio de dólares gastados = 50.86*2- 316.75* + 541.48,
en donde x representa cada periodo de 4 añas desde 1948.
Sustituya x por 1 para obtener el monto gastado en 1952,
x por 2 para obtener el monto gastado en 1960,y asísuce
sivamente.
a) Determine el monto gastado en las elecciones de 1976.
b) Calcule la cantidad que se gastará en las elecciones de
2004.
66. Tránsito ferroviario El tránsito ferroviario en Estados
Unidos ha aumentado de manera continua, duplicándose
desde 1965. La razón principal de esto es el incremento de
tos trenes utilizados para transportar bienes por medio de
contenedores. Podemos calcularel monto de la carga trans
portada en toneladas-milla (1 tonelada-milla es igual a
1 tonelada de carga transportada a lo largo de una milla)
por medio de esta ecuación
carga transportada = 14.04*2 + 1.96* + 712.5
en donde * representa cada periodo de 5 años desde 1960.
Sustituya x por 1 para obtener la cantidad de carga en
1965, * por 2 para obtener la cantidad de carga transpor
tada en 1970, * por 3 para 1975,etcétera.
a) Determine la cantidad de carga transportada por vía
ferroviaria en 1980.
b) Determine la cantidad de carga transportada por vía
ferroviaria en 2000.
[1.5] Simplifique cada expresión y escriba la respuesta sin exponentes negativos.
67. 23-22 68. *2-* 3 69.
a1
2
fl4
70.
y 2
y
7L
b1
b-2 72. c3*c-5 73. 5“2•5-1 74 3*°
75. ( - 2 m3)2 76.
r 77.
(ir 78.
W
79. ( 5 x y 3) ( - 3 x 2y ) 80. (2v3w~4)(5v~6w) 8L
6 * - y
2 x2y ~ 2
82.
1 2 x ~ 3y~*
4 *- y
83.
g -2h - 'f
84.
21m~3n 2
7 //T V
85. 86.
m
87.
( pV Y ( - 2 a b - > V ( * x y 3 2
90.
í 9m~2n V
U v J
88.
l c2 )
89.
* ) 3mn )
9L (—2m2#T3)"’2 92.
( i 5 * w 2v
V-3*yvy
93.
(2 x-y z* y
3 x * y ~ 2z~ 2)
94
(8x-yy](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-91-320.jpg)
![6 4 • Capítulo 1 • C o n c e p to s básicos
[1.6] Exprese cada número en notación científica.
95. 0.0000742 96. 260,000 97. 183,000 98. 0.000001
Simplifique cada expresión y exprese la respuesta sin exponentes.
18 X 103
99. (25 X 10_3)( 1.2 X 106) 100.
9 X 105
10L
4,000,000
0.02
102. (a004)(500,000)
103. Publicidadpor televisión Los fabricantes de automóviles
gastan millones de dólares cada año en publicidad televi
siva. En el segundo trimestre de 2001, los"tres grandes” fa
bricantes de automóviles de Estados Unidos gastaron los
sguientes montos en anuncios por televisión:General Mo
tors - $2.64 X 108;Ford - $1.51 X 108,y Daimler Chrys
ler - $9.2 X 107.
a) ¿Cuánto más gastó General Motors en comparación
con Ford?
b) ¿Cuánto más gastó Ford en comparación con Daimler
Chrysler?
c) ¿Cuántas veces es mayor la cantidad que gastó General
Motora que la cantidad que gastó Daimler Chrysler?
n i Í3JA2 t ..
104. Voyager El 17de febrero de 1998, la astronave VoyagerI
se convirtió en el explorador más distante del sistema so-
Examen de práctica del capítulo
lar, rompiendo el récord del Pioneer 10. El Voyager 1,con
20 años de edad, ha recorrido más de 1.04 X 10'° kilóme
tros desde laTierra (alrededor de 70 veces la distancia en
tre el Sol y laTierra).
a) Represente 1.04 X 10'°como un número decimal.
b) ¿Cuántos miles de millones de kilómetros ha viajado
el Voyager 1.
c) Suponiendo que el Voyager 1 ha recorrido aproxima
damente el mismo número de kilómetros cada uno du
rante sus 20 de vida, ¿cuántos kilómetros recorrió en
promedio en un año?
d) Si 1 kilómetro =5 0.6 millas, ¿qué tan lejos, en millas,
ha viajado el Voyager 11
L Escriba en forma de lista A = {x|x es un número natural mayor que o igual a 6}.
Indique si cada afirmación es verdadera o falsa.
2. Todos los números reales son números racionales. 3. La unión del conjunto de los números racionales y el con
junto de los números irracionales es el conjunto de los nú
meros reales.
Considere el conjunto de números {- 1,2, -4 ,0 , Jf, 257, V 8, V 2, -1.92}. Liste los elementos del conjunto que sean,
4. números racionales. 5. números reales.
Determine A U B y A IT B para los conjuntos A y B.
6. A = {8,10,11,14}, B = {5,7,8,9,10} 7. A = {1,3,5,7, ...},B = {3,5,7,9,11}](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-92-320.jpg)
![E x a m e n de práctica del capítulo • 6 5
En los ejercicios 8 y 9, ilustre cada conjunto en la recta numérica*
8. {*|-2.3 * < 5.2}
>. | * < * < f y * e Z
2 5
10. Liste de menor a mayor: |3|, -|4 |, -2.6.
Señale el nombre de cada una de las siguientes propiedades.
1L (* + y) + 3 = * + (y +3)
12. 3* + 4y = 4y + 3*
Evalúe cada expresión.
13. {4 — [7 —32 (32 —2*3)]}
14 24 + 42 -r 2? • y/25 + 7
-3 |4 - 8| h
- 2 + 4
15.
16.
-V 5 6 + 18 - 32 + 4
- ó 2 + 3(4 - |6|) - 6
4 - ( - 3 ) + 12 H-4*5
17. Evalúe + 2*y + y2cuando * = 2 y y = 3.
18. Devolución de impuestos Desde 1990,el promedio de de
volución de impuestos federales se ha incrementado en
Estados Unidos. El reembolso promedio de 1990 a 2002
puede calcularse por medio de
devolución promedio de impuestos federales =
Ó.42*2 + 13.9* + 970
en donde * representa el número de años desde 1990. Sus
tituya * por 1 para calcular la devolución promedio de im
puestos federales en 1991, * por 2 para estimar la
devolución promedio de impuestos federales en 1992, y
así sucesivamente.
a) Calcule la devolución promedio de impuestos federa
les en 1995.
b) Calcule la devolución promedio de impuestos federa
les en 2002.
Simplifique cada expresión y escriba la respuesta sin expo
nentes negativos.
2
19. 3"2
24a2b~3c°
2L
30a3b2c-2
20.
22.
4ni- 3
n
- 3 *3y
x - y
- 2 - 3
23. Cbnvierta 242,000,000 a notación científica.
3.12 X 106
24. Simplifique -p------ —
—
¿y escriba el número sin expo-
1.2 X lu
nentes.
25. Empleo por género El número total de personas
empleadas en Estados Unidos en 2000 fue alrededor de
1.41 X 108. La gráfica muestra la división hombres / mu
jeres.
a) ¿Cuántos hombres fueron empleados?
b) ¿Cuántas mujeres fueron empleadas?
c) ¿Cuántos hombres másque mujeres fueron empleados?](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-93-320.jpg)



![Sección 2.1 • Resolución d e e cu a cio n e s lineales • 6 9
E J E M P L O 1
Solución
E J E M P L O 2
Solución
Ejemplos de reducción de térm inos semejantes
5 * - 2 x = (5 - 2 ) * = 3*
3 x 2 - 5 x 2 = (3 - 5 ) ^ = -2x>
- 7 x 2y + 3 ¿ y = ( - 7 + 3) x 2y = - 4 x 2y
4 ( x - y ) - ( x - y ) = 4 ( x - y ) - l ( x - y ) = (4 - l) ( x - y ) = 3 ( x - y)
Al simplificar expresiones,podem os reordenar los térm inos aplicando las propie
dades conm utativa y asociativa q u e se analizaron en el capítulo 1.
Simplifique. Si una expresión no puede simplificarse, dígalo.
a) - 2 x +5 + 3x - 7 b) l x 2 - 2 x 2 + 3 x + 4 c) 2x - 3y + 5* - 6y + 3
a) ~ 2 x + 5 + 3 x — 7 = ~ 2 x + 3 x + 5 — 1 ColoqueJuntos loe términoseemejantee.
x -2
E sta expresión se simplifica y resulta x - 2.
b) - l x 2 + 3 x + 4 = 5 x 2 + 3 x + 4
c ) 2 x - 3 y + 5 x - 6 y + 3 = 2 x + 5 x - 3 y - 6 y + 3
= l x - 9 y + 3
ColoqueJuntoe loe térmlnoe
eemejantee.
AHORA RESUELVA EL E JER CIC IO 55
Simplifique - 2 (a + 7) - [ - 3 {a - 1) + 5].
- 2 (a + 7) - [ - 3 (a - 1) + 5] = - 2 (a + 7) - l [ - 3 {a - 1) + 5]
= - 2 a - 14 - l [ - 3 a + 3 + 5]
Propiedad dietributlva.
= —2a — 14 — 1 [—
3a + 8] Peduclmoe loe térml
noe eemejantee.
= —2a — 14 + 3 — 8 Propiedad dietrlbutiva.
= a — 22 Peduclmoe loe térmlnoe eemejantee. ^
3 R e s o lv e r e c u a c io n e s lineales
U na ecuación es una proposición m atem ática d e igualdad. Las ecuaciones deben con
tener un signo de igual y una expresión m atem ática a cada lado del mismo.
Ejemplos de ecuaciones
* + 4 = - 7
2 x2 - 4 = - 3 x + 5
Los núm eros q u e hacen q u e una ecuación sea una proposición verdadera, se lla
m an soluciones o raíces d e la ecuación. E l conjunto solución d e una ecuación es el
conjunto d e núm eros reales q u e hacen q u e la ecuación sea verdadera.
Ecuación Solución Conjunto solución
2a: + 3 = 9 3 {3}
Cuando dos o más ecuaciones tienen el mismo conjunto solución, se dice que
son ecuaciones equivalentes. Por lo general las ecuaciones se resuelven iniciando con
la ecuación dad a y produciendo una serie d e ecuaciones equivalentes más simples.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-97-320.jpg)


![7 2 • Capítulo 2 • E c u a c io n e s y desigualdades
4 x - 4.0 = 5.6*
4 x - 4 x - 4.0 = 5.6* - 4x
- 4 .0 = 1.6*
- 4 .0 = L 6*
1.6 1.6
- 2 .5 = *
Peete 4 x en amboe ladoe.
Ovidaamboe ladoeentre 1.6 .
L a solución es -2 .5 . #
Para ahorrar espacio, en este libro no se m ostrará siem pre la com probación de
las respuestas, pero usted sí deb e verificarlas todas. C uando la ecuación contenga nú
m eros decimales, puede utilizar una calculadora p ara resolver y verificar la ecuación
m ás rápido.
C ó m o utilizar su c a lcu la d o ra
••••
Com p ro b a ció n d e soluciones p o r sustitución
Las soluciones d e las ecuaciones pueden com probarse p o r medio d e una calculadora. Para verificar, sustituya la
variable d e am bos lados d e la ecuación con su resultado p ara ver si obtiene el mismo valor (algunas veces puede
haber una pequeña diferencia en los últimos dígitos). L a pantalla d e la calculadora graficadora d e la figura 2.1
m uestra am bos lados d e la ecuación dad a en el ejem plo 5,con un resultado d e -2 2 .4 cuando x se sustituye con -2.5.
Por lo tanto, la solución -2 .5 satisface la ecuación.
4 (x - 3.1) = 2.1 (* - 4) + 3.5*
4( —
2.5 - 3.1) = 2.1 ( —
2.5 - 4 ) + 3 .5 (-2 .5 )
KK - 2 . 5 - 3 . 1>
- 2 2 .4
2 . 1< - 2 .5 - 4 > + 3 .5 *
- 2 .5
- 2 2 .4
Valordel ladoIzquierdo
de laecuación.
Valordel ladoderecho
de la ecuación.
Ejercicios
Utilice su calculadora p ara determ inar si el número
dado es la solución d e la ecuación.
L 5.2(* - 3.1) = 2 .3 (* - 5.2); 1.4
2. -2 .3 ( 4 - * ) = 3.5(* - 6.1); 10.125
FIGURA 2.1
E J E M P L O 6
Solución
A continuación resolverem os un ejem plo q u e contiene paréntesis anidados.
Resuelva la ecuación 7c - 15 = -2 [6 (c - 3 ) - 4 (2 - c)].
7c - 15 = - 2 [6 ( c - 3) - 4 (2 - c)]
Propiedaddietributiva.
Reduccióndetérminoeeemejantee.
Propiedaddietributiva.
AHORA RESUELVA EL EJER CIC IO 91
1c - 15= -2 [6 c - 18 - 8 + 4c]
1 c - 15= -2 [1 0 c - 26]
7 c - 15= -2 0 c + 52
7c + 20c - 15= -2 0 c + 20c + 52
27c - 15 = 52
27c - 15 + 15 = 52 + 15
27c = 67
27c = 67
27 27
67
27
Sume 20c en amboe ladoe.
Sume 15en amboe ladoe.
Dividaamboe ladoe entre 27.
c =](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-100-320.jpg)




![Sección 2.1 • Resolución de e c u a c io n e s lineales • 7 7
3L 6 32. - 3 33. -5 * 3 4 18 * V
35. 5a2b*c 36. *4y6 37. 3x5y 6z 38. - 2 x*y7z?
Simplifique cada expresión. Si una expresión no puede simplificarse, indíquelo.
39. 7r + 3 b - 11* +12y 40. 3x2 + 4* + 5 41. 5*2 - 3x + 2x - 5
42. l i a - 126 - 4c + 5a 43. 10.6c2- 2.3c + 5.9c - 1.9c2 4 4 l y + 3x - 7 + 4* - 2y
45. 103+ ic2- íe + 1 46. b + b2 - 4b + b2 + 3b 47. 6p q - 7pq + p + q
48. 7 * V + 11y3*2 49. 1 2 ^ | + - d 50. 4.3 - 3.2* - 2(x - 2)
5L 3^.t + j ) - j * + 5 52. 6n + 0.6(n - 3) - 5(n + 0.7)
- 53. 4 - [6(3* + 2) - *] + 4 54 3(* + y) - 4 (* + y) - 3
55. 4* - [3* ~ (5* - 4y)] + y 56. -2 [3 * - (2y - 1) - 5x ] + y
57. 5b - {7[2(3¿> - 2 ) - (4b +9)] - 2} 58. 2{[3a - (2b - 5a)] - 3(2a - ¿>)}
59. —{[2rs - 3(r + 2s)]- 2(2r 2- s)} 60. p2q + 4pq - [ - ( p q + 4p2g) + pq]
Resuelva cada ecuación.
61. 5a - 1 = 14 61
Si
*
+
3 + * = 9 63. 5* - 9 = 3(* - 2)
64 5s - 3 = 2s + 6 65. 4* - 8 = -4 (2 * - 3) + 4 66. S w + 7 = -3 to - 4
67. - 6 (z - 1) = - 5 (z + 2) 68. 7(* "- 1) = 4(* + 2) 69. - 3 (/ - 5) = 2 (t - 5)
70.
+
H
C
-¡
1
II
1
H
7L 3* + 4(* - 2) = 4* - 5 72. 6(9 - 3) = - 4 (q + 2)
73. 2 - (* + 5) = 4* - 8 74 4* - 2(3* - 7) = 2* - 6 75. P ~ (P + 4) = 4(p - 1) + 2p
76. 8* + 2 (x - 4) = 8* + 10 77. -3(>r - 1) + 2y = 4(y - 3) 78. 5r - 13 - 6r = 3(r + 5) - 16
79. 6 - (* + 3) = 3* + 5 - 2* 80. 8 - 3(2* - 4) = 5 + 3* - 4* 8L 4(2* - 2) - 3(* + 7) = - 4
82. - 2 ( 3 w + 6) - (4ic - 3) = 21 83. -4 (3 - 4*) - 2(* - 1) = 12* 84. -4 (2 z - 6) = -3 (z - 4) + z
85. 5(a + 3) - a = - (4a - 6) + 1 86. 3(2* - 4) + 3(* + 1) = 9 87. 5(* - 2) - 14* = * - 5
88. 3[6 - (h + 2)] - 6 = 4 ( - h + 7) “ 89. 2[3* - (4* - 6 ) ] = 5(* - 6)
90. - z - 6z + 3 = 4 - [6 - z - (3 - 2z)] 91. 4{2 - [3(c + 1) - 2(c + 1)]} = -2 c
92. 3{[(* - 2) + 4*] — (jc —3)} = 4 - (* - 12) 93. -{ 4 (d + 3) - 5[3d - 2(2d + 7)] -8 } = -lO d - 6
94 -3 (6 - 4*) = 4 - {5* - [6x - (4* - (3* + 2))]}
Resuelva cada ecuación. Si su respuesta no es un entero, déjela como una fracción.
95. ^ = -1 6 96. 3 = 2 97. — ^ 2 = - 6 98. | ( 6 * - 10) = 7
99. j í + = 39 100. ^ (* - 2) = ^ (2 * + 6 ) 10L 4 - | * = 7
102. a: - 2 = | ( * + 4) £¡ 103. | = | * - ^ 104. | m - ^ + |
Resuelva cada ecuación. Redondee las respuestas al centésimo más cercano.
105. 0.4* + 4.7 = 5.1* 106.0.2(* - 30) = 1.6*
107. 4.7* - 3.6(* - 1) = 4.9 108. 6.1p - 4.5(3 - 2p) = 15.7](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-105-320.jpg)
![7 8 • Capítulo 2 • E c u a c io n e s y desigualdades
109. 5(z + 3.41) = -7.89(2z - 4) - 5.67 110. 0.05(2000 + 2*) = 0.04(2500 - 6*)
111. 0.6(500 - 2.4*) = 3.6(2* - 4000) 112. 0.42* - * = 5.1(* + 3)
113. 1000(7.34*7 + 14.78) = 100(3.91 - 4.21?) 114. 0.6(14* - 8000) = -0.4(20* + 12,000) + 20.6*
Determine el conjunto solución para cada ejercicio. Luego indique si la ecuación escondicional, inconsistente o una identidad.
115. 3(y + 3) - 4(2y - 7) = - 5 y + 2 116. 4* + 12 - 8* = -6 (* - 2) + 2*
117. 4(2* - 3) + 5 = -6 (* - 4) + 12* - 31 118. -5 (c + 3) + 4<c - 2) = 2(c + 2)
119. - { - b + 7) - 6( b + 3) = - 5 ( b + 5) 120. - [ 4 - (* - 2)] = 2* - 2 - *
£ 121. 6(* - 1) = -3 (2 - *) + 3* 122. 6(z + 5) - 5(z + 2)= -3 (z + 1) + 4(z - 5)
123. - 5 (d - 4) + 3d - 5 = 3{d + 1 - 2d)+ d 124. 4(2 - 3*) = -[6 * - (8 - 6*)]
Resolución de problemas
w 125. Bebés dormilones El doctor Richard Ferber, un pediatra
experto en problemas del sueño, ha desarrollado un méto
do* para ayudar a los niños, de 6 meses de edad en adelan
te, a dormir toda la noche. Conocido como "Ferberizing”,
este método consiste en que los padres deben esperar in
tervalos de tiempo cada vez más grandes antes de entrar
a la habitación del niñopara consolarsu llanto durante la
noche. El tiempo sugerido de espera depende de cuántas
noches se ha utilizado el método, y puede determinarse
por medio de la ecuación
W = 5n + 5
en donde W esel tiempo de espera en minutos y n es el nú
mero de noches. Por ejemplo, la primera noche es n = 1,
lasegunda noche es n = 2, etcétera.
a) ¿Cuánto deben esperar los padres la primera noche?
b) ¿Cuánto deben esperar la cuarta noche?
c) ¿En qué noche los padres deben esperar 30 minutos?
d) ¿En qué noche deben esperar 40 minutos?
sucesivamente. Si la densidad de población continúa en
aumento a la tasa actual,
a) determine la densidad poblacional de Estados Unidos
en 2005.
b) ¿en que año la densidad poblacional de Estados Uni
dos llegará a 100personas por milla cuadrada?
127. Participación de mercado de losfabricantes de automó
viles Desde 1993, los fabricantes estadounidenses de au
tomóviles han ido perdiendo parte del mercado ante sus
competidores de Asia y Europa. Del total de automóvi
les vendidos en Estados Unidos,el porcentaje que corres
ponde a los autos de fabricacióndoméstica puede estimarse
usando la ecuación
M = -1.26* + 75.34
en donde M es el porcentaje de automóviles de fabrica
cióndoméstica del total vendido en Estados Unidos, y * es
el número de años desde 1993. Utilice * = 1 para 1994,
* = 2 para 1995,etcétera.
a) ¿Qué porcentaje del total de automóviles vendidos en
Estados Unidos corresponde a autos de fabricacióndo
méstica en 2003?
b) ¿En qué año el porcentaje de autos de fabricación
doméstica será de 58.%% sobre el total de ventas en
Estados Unidos?
126. Densidadpoblacional La densidad poblacional de Esta
dos Unidos ha aumentado de manera constante desde
1990,y puede estimarse por medio de la ecuación
P = 0.8l í + 70.4
en donde P es la densidad poblacional, es decir, el núme
rode personas por milla cuadrada, y i es el número de años
desde 1990. Utilice t = 1para 1991, t = 2 para 1992, y así
•Antes de utilizareste método, los padres deben consultar a un médico pediatra.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-106-320.jpg)
![Sección 2 .2 • Resolución d e p roblem as y u so d e fórm ulas • 7 9
128. Pensiones Las pensiones son seguros de vida que garan
tizan pagos futuros. Una de sus variantes,denominada pen
sión variable, es una cuenta de retiro que permite invertir
en un fondo mutualista y diferir el pago de impuestos has
ta que se realicen los retiros en el futuro. El número de
personas que opta por este tipo de pensiones ha aumen
tado de manera constante en los años recientes, y su núme
ro puede calcularse mediante la ecuación
S = 10* + 20
en donde S representa la venta total de pensiones varia
bles (en miles de millones de dólares), y x es el número
de años desde 1991. Utilice x = 1 para 1992, x = 2 para
1993, etcétera.
a) Determine la venta total de pensiones variables en 2001.
b) ¿En qué año la venta de este tipo de pensión alcanza
rá los 140 mil millones de dólares?
129. Población deJamestown La poblacióndel municipio de
Jamestown, en Wisconsin, ha estado creciendo paulatina
mente desde 1996. La población puede calcularse usando
la ecuación
P = 7* + 2170
en donde P es la poblacióndel municipiode Jamestown y x
es el número de años desde 19%. Utilice x = 1para 1997,
x = 2 para 1998,y así sucesivamente.
a) ¿Cuál fue la población en 2003?
b) Sicontinúa la misma tasa de crecimiento, ¿en qué año
la población llegará a 2240 habitantes?
130. Cbnsidere la ecuación x = 4. Proporcione tres ecuaciones
equivalentes. Explique por quéson equivalentes.
131. Cbnsidere la ecuación 2x = 5.Proporcione tres ecuaciones
equivalentes. Explique por quéson equivalentes.
132. Invente una ecuaciónque sea una identidad. Explique có
mo creó la ecuación.
133. Invente una ecuación que sea inconsistente. Explique có
mo creó la ecuación.
134. Cree una ecuacióncon tres términos a la izquierda del sig
no igual y dos términos a la derecha, y que sea equivalen
te a la ecuación 3x + 1 = x + 5.
135. O ee una ecuacióncon dos términos a la izquierda del sig
no igualy tres términos a la derecha, y que sea equivalen
te a la ecuación x + 3 = 6.
136. En la ecuación-3(x + 2) + 5x + 12 = n, ¿qué número real
debe ser n
para que la soluciónsea 6? Explique cómo de
terminósu respuesta.
137. En la ecuación 2(x + 5) + n = 4x - 8, ¿qué número real
debe ser n para que la solución sea -2 ? Explique cómo
determinósu respuesta.
138. En la ecuación f + J = 2, ¿qué número real debe ser n
para que la solución sea x = 2? Explique cómo determi
nósu respuesta.
Resuelva cada ecuación para el símbolo dado. Suponga que el símbolo que despeja representa la variable, y que todos los demás
símbolos representan números reales diferentes de cero. Vea el ejemplo 11.
139. D e* A - □ = ©despeje A.
141. De © □ + A = 0 despeje O.
140. De A (O + □) = 0 despeje A.
142. De A (O + □) = 0 despeje □.
Ejercicios de repaso acumulativo
[1.3] 143. a) Explique con sus propias palabras cómo se de
termina el valor absoluto de un número,
b) Escriba la definiciónde valor absoluto.
[1.4] Evalúe.
144. a) - 3 2
145. ^ = 6 4
3 3
146. -
b) ( - 3 ) 2
2 . 2 R E S O L U C IÓ N D E P R O B L E M A S Y U S O D E F Ó R M U L A S
2 f e
1 Usar ©I procedimiento para resolución de problemas.
2 Despejar una variable en una ecuación o fórmula.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-107-320.jpg)










![9 0 • Capítulo 2 • E cu a cio n e s y desigualdades
86. Prueba de esfuerzo Qiando un médico realiza una prue
ba de esfuerzo en un paciente, sabe que, cuando su ritmo
cardiaco llegue a cierto punto, deberá interrumpirla. El
máximo ritmo cardiaco permitido, m,en latidos por minu
to, puede calcularse mediante la ecuación m = -0.875* +
190,en donde * representa la edad del paciente de 1 a 99
años. Usando este modelo matemático, determine
a) el ritmo cardiaco máximo permitido para un persona
de 50 años.
b) la edad de una persona cuyo ritmo cardiaco máximo
permitido es de 160 latidos por minuto.
87. Saldo de una cartera de inversión Algunos especialistas en
finanzas recomiendan la siguiente regla a los inversionis
tas. De su inversión total, el porcentaje de acciones debe
ssr igual a 100 menos su edad; el resto debe ser colocado
en bonos o mantenerse en efectivo.
a) Construya modelos matemáticos para calcularqué por
centaje debe conservarse en acciones (utilice S para re
presentarel porcentaje de acciones y a para representar
la edad de la persona).
b) Utilizando la regla mencionada, determine el porcen
taje en acciones que debe poseer una persona de 60
años.
índice de masa muscular El índice de masa muscular es
una método estándarpara calcular el peso corporal de una
persona respecto de su estatura. Para determinar su índi
ce de masa corporal (IMC) usando medidas métricas, di
vida su peso (en kilogramos) entre su estatura (en metros)
elevada al cuadrado. Una forma abreviada para calcular el
IMC usando libras y pulgadas, consiste en multiplicar por
705 su peso (en libras) y luego dividir el resultado entre el
cuadrado de su altura (en pulgadas).
a) Cree una fórmula para determinar el IMC de una per-
a>na usando kilogramos y metros.
b) Cree una fórmula para determinar el IMC de una per
sona cuando el peso está dado en libras y la altura en
pulgadas.
c) Determine su IMC.
Reto
s/t
89. En la ecuación r = despeje a) s, b) u.
Ejercicios de repaso acumulativo
[1.4] 90. Evalúe - V 3 2 + 42 + |3 - 4| - 52.
7 + 9 h
- (23 + 4 4)
9L Evalúe
|3 —7| + V 5 2 - 32 ’
92. Evalúe <f - 3a2b + 3ab2- b3cuando a = -2 , b = 3.
[2.1] 93. Resuelva la ecuación + = ^ ~
2 . 3 A P L IC A C IO N E S D E L Á L G E B R A
f i f e
1 Traducir una proposición verbal a una expresión algebraica o a
una ecuación.
2 Utilizar el procedimiento para resolución d e problemas.
1 T ra d u c ir u n a p ro p o s ic ió n v e rb a l a u n a e x p re s ió n a lg e b ra ic a o a u n a e c u a c ió n
E n las siguientes secciones se presentarán algunos d e los m uchos usos del álgebra en
situaciones d e la vida real. Cuando sea posible, incluiremos otras aplicaciones relevan
tes a lo largo del texto.
Q uizá la parte más difícil al resolver un problem a verbal,consiste en transform ar
lo en una ecu ació a Éste es el paso 2 del procedim iento para resolución d e problem as
qu e se presentó en la sección 2.2. A ntes d e representar los problem as com o ecuacio
nes, darem os algunos ejem plos d e frases representadas com o expresiones algebraicas.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-118-320.jpg)













![Actividad en equipo______________
104. • C apítulo 2 • E c u a c io n e s y desigualdades
Analice y responda en equipo el ejercicio 54.
54, a) Cada miembro del equipo seleccione un número. Lue
go multiplíquelo por 2, sume 33, reste 13,divida entre
2 y reste el número con que inició. Registre cada res
puesta.
b) Ahora comparen las respuestas.Si no obtuvieron la mis
ma respuesta, verifiquen cada uno el trabajo del otro.
c) Expliquen en equipo por qué este procedimiento tie
ne como resultado una respuesta de 10 para cualquier
número real n seleccionado.
Ejercicios de repaso acumulativo
[1.3] Resuelva.
55. 2 + - | 56. -6 .4 - (-3 .7 ) 57. -2 58. 5 - |—
3| -
[1.5] 59. Simplifique (2x4y~6)~3.
2 . 4 P R O B L E M A S A D IC IO N A L E S D E A P L IC A C IÓ N
£ É É j
1 Resolver problem as d e movimiento
2 Resolver problem as de m ezclas
E n esta sección analizarem os dos tipos adicionales d e problem as d e aplicación: proble
m as d e movim iento y d e mezcla. Los hem os colocado en la misma sección, porque se
resuelven utilizando procedim ientos similares.
1 R esolver p ro b le m a s d e m ovim iento
U na fórm ula con m uchas aplicaciones útiles es
cantidad = velocidad • tiempo
La “cantidad” en esta fórm ula puede ser una m edida d e m uchas cantidades di
ferentes, dependiendo de la tasa d e cambio (o velocidad). Por ejemplo, si la tasa se mi
d e en distancia por unidad d e tiem po, la cantidad será la distancia. Si la tasa se m ide
en volum en p o r unidad d e tiem po, la cantidad será volum en, etcétera.
Cuando aplique esta fórm ula, asegúrese d e q u e las unidades son consistentes.
Por ejemplo, cuando hablam os acerca d e una copiadora, si la velocidad está dad a en
copias p o r m inuto, el tiempo deb e estar dado en minutos. Los problem as q u e pueden
resolverse con esta fórm ula se denom inan problem as de m ovim iento,ya q u e incluyen
movim iento, a una tasa constante, durante cierto periodo.
U na enferm era q u e aplica a su paciente un suero vía intravenosa puede utilizar
esta fórm ula p ara determ inar la tasa de goteo del fluido q u e está siendo inyectado.
U na com pañía d e perforación d e pozos petroleros o d e agua puede em plear esta fór
m ula p ara determ inar la cantidad d e tiempo necesaria p ara alcanzar su meta.
Cuando la fórm ula d e movim iento se utiliza p ara calcular distancia, la palabra
cantidad se reem plaza con el térm ino distancia, y la fórm ula se denom ina fórm ula de
distancia.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-132-320.jpg)









![114 • C apítulo 2 • E c u a c io n e s y d esigualdades
¿a qué horadebe lanzarse elsegundo cohete si ambas naves
cfeben reunirse a una distanciade 38,000 millasde laTierra.
a) Explique cómo encontró lasoluciónpara este problema.
b) Determine la solución del problema.
47. a) Invente su propio problema de movimiento que pue
da representarse como una ecuación.
b) Escriba la ecuaciónque representa a su problema.
c) Resuelva la ecuación y luego determine la respuesta a
su problema.
48. a) Invente su propio problema de mezclas que pueda re
presentarse como una ecuación.
b) Escriba la ecuaciónque represente su problema.
c) Resuelva la ecuación y luego determine la respuesta a
su problema.
Reto
49. Distancia a Calais El Eurotúnel (túnel submarino que 50. Automóviles de carreras Dos automóviles, A y fí.partici-
comunica Folkestone, Inglaterra, con Calais, Francia) tiene pan en una carrera de 500 vueltas; cada vuelta cubre una
31 millas de longitud. Una persona puede abordar el tren distancia de 1 milla. El automóvil que va adelante, A ,pro-
bala en París,viajarsin parar a través del Eurotúnel y llegar media 125 millas por hora cuando llega a la mitad de la
a Londres en 3 horas. El tren bala recorre la distancia entre carrera;el automóvil B estáexactamente 62 vueltas detrás
a) Determine la velocidad promedio del automóvil B.
b) Cuando el automóvil A llega a la mitad de la carrera,
¿qué tan lejos de él, en segundos, está el automóvil B1
5L Solución anticongelante El radiadorde un automóvil tiene
una capacidad de 16 cuartos de galón. En este momento
está Heno con una solución anticongelante con concentra
ción de 20%. ¿Cuántos cuartos deben drenarse y reempla
zarse con anticongelante puro para hacer que el radiador
contenga una solución anticongelante con concentración
de 50%?
Distancia a Calais El Eurotúnel (túnel submarino que
comunica Folkestone, Inglaterra, con Calais, Francia) tiene
31 millas de longitud. Una persona puede abordar el tren
tala en París,viajarsin parar a través del Eurotúnel y llegar
a Londres en 3 horas. El tren bala recorre la distancia entre
Parísy Calais en un promedio de 130 millas por hora; des
pués reduce su velocidad a un promedio de 90 millas por
lora a lo largo del trayectode31 millasdel Eurotúnel. Cuan-
cb sale del Eurotúnel, cubre el trayecto de 68 millas entre
folkestone y Londres a un promedio de 45 millas por hora,
cbbido a que transita por víasobsoletas. Con esta informa
ción, determine la distancia que hay entre París y Calais.
Ejercicios de repaso acumulativo
2 .7 X 1 0 15
[1.6] 52. Exprese el cociente en notación científica. - 1
- ---- —j
4 .5 X 1™
Resuelva
[2.1] 53. 0.6* + 0.22 = 0.4(* - 2.3)
2 1
54. - x + 3 = x + -
3 2
[2.2] 55. Despeje y en la ecuación ~ (x - 2) = ~(2x + 3y)
[2.3] 56. Renta de un camión La agencia de renta de camio
nes Transportes, S. A. cobra $30 por día más $0.14
por milla recorrida. Por su parte, la agencia Camio
nes, S. A. cobra $16 por día más $0.24 por milla re
corrida. ¿Qué distancia debería conducir en 1 día
para que el precio de Transportes, S. A. sea igual al
de Camiones, S. A.?
para y.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-142-320.jpg)

![1 1 6 • C apítulo 2 • E c u a c io n e s y d esigualdades
que am bos lados d e una desigualdad pueden multiplicarse o dividirse p o r cualquier nú
m ero real positivo. Las dos últimas propiedades indican que cuando am bos lados de
una desigualdad se m ultiplican o dividen p o r u n n ú m ero negativo, la dirección d e la d e
sigualdad se invierte.
Ejem plo d e multiplicación
por un n úm e ro negativo
Multiplique ambos lados
de a desigualdad poi— I
e invierta la dirección del
símbolo de desigualdad.
4 > - 2
- 1 ( 4 ) ( - 2)
- 4 < 2
Ejem plo d e división entre
un núm ero negativo
10
10
- 2
- 5
- 4
- 4
Divida ambos lados de la
desigualdad entre -2
e Invierta la dirección de!
símbolo de desigualdad.
S U G E R E N C I A No olvide invertir la dirección del símbolo de desigualdad cuando multiplique o divi
da ambos lados de la desigualdad por un número negativo.
Dirección del sím bolo de
Desigualdad la desigualdad
-3 * 6
-3 * < 6 — - > —
- 3 -3
" f > 5 ( - 2 ) ( - § ) < ( - 2 ) ( 5 )
E J E M P L O 1
Solución
Resuelva la desigualdad 5f - 7 > -2 2 .
5 í - 7 ^ - 2 2
5í - 7 + 7 > - 2 2 + 7
51 > - 1 5
51 - 1 5
— > ------
5 5
t > - 3
Sume 7 en ambos lados.
Divida ambos lados entre 5.
E l conjunto solución es {tt > -3 } . Cualquier núm ero real m ayor q u e o igual a - 3 sa-
AHORARESUELVAELEJERCICI017 tisface la desigualdad.
2 Representar soluciones gráficamente en la recta numérica, notación de inter
valo y conjuntos solución
Com o se indicó en la sección 1.2, la solución d e una desigualdad puede representarse
gráficam ente sobre una recta num érica, o escribirse com o un conjunto solución. La
solución tam bién puede escribirse en notación d e intervalo, com o se ilustra a conti
nuación. Casi todos los profesores tienen preferencia p o r alguna d e estas form as para
indicar la solución d e una desigualdad.
Recuerde que en la recta numérica, un círculo relleno indica que elpunto extremo es
parte de la solución, y un círculo vacío indica que elpunto extremo no es parte de la solu
ción. En notación de intervalos se utilizan los corchetes, [ ],para indicar que lospuntos ex
tremos son parte de la solución, y los paréntesis, ( ) , para indicar que los puntos extremos
no son parte de la solución. El símbolo oo,que se lee “infinito”,indica que el conjunto so
lución continúa indefinidamente. C ada vez que se utilice el símbolo ooen notación de in
tervalo,debemos usar un paréntesis del lado correspondiente de esta notaciónde intervalo.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-144-320.jpg)
![S e cció n 2 .5 • Resolución d e d e sigu a lda des lineales * 1 1 7
Solución de
desigualdad
x > a
x > a
x < a
x < a
a < x < b
a < x < b
a < x < b
a < x < b
x > 5
* < 3
2 < x 6
- 6 x < - 1
Conjunto
solución indicado
en la recta numérica
— 4 —
- l <
• ■ 1 1 1 -t
) 1 2 3 4 :
> ■ i t i ---------►
> 6 7 8 9 10 11
- 6 - 5 - 4 - 3 - 2 - 1 11 1 2 3 4 5 6
- 3 - : ’ -1 0 1 2
1
1 4 5 6 7 8
»— t— * 1 :
9
Conjunto
solución representado
en notación de intervalo
(a, oo)
[a, oo)
( - o o , a)
( - o o , fl]
(a, b)
[a,b]
(a, b]
[a, b)
[5, oo)
( —0 0 ,3 )
( 2. 6]
[ - 6. - 1]
- 9 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3
E n el siguiente ejem plo resolverem os una desigualdad q u e tiene fracciones.
E J E M P L O 2 Resuelva la siguiente desigualdad y d é la solución tanto en la recta num érica com o en
notación d e intervalo.
1 1 2 z „
4Z ~ 2 K T +2
Solución Podem os elim inar las fracciones d e una desigualdad al m ultiplicar am bos lados d e la
desigualdad p o r el m ínim o com ún denom inador, M CD, d e las fracciones. E n este
caso multiplicam os am bos lados d e la desigualdad p o r 12. Luego resolvemos la desi
gualdad resultante, tal com o hicim os en el ejem plo anterior.
1 1 2 z „
? Z " 2 < T + 2
i2lW ) <i2if +
2
2z Multipliqueambos
ladoe porel MCD, 12.
Propiedad distributiva.
3 z ~ 6 < 8z + 24
3 z ~ 8 z ~ 6 < 8 z ~ 8 z + 2 4 Peste &zen ambos lados.
~ 5 z - 6 < 24
- 5 z - 6 + 6 < 2 4 + 6
- 5 z < 30
Sume & en ambos lados.
- 5 z . 30
- 5 - 5
z > - 6
Dvida ambos lados entre —5
y cambie ladirección del
símbolode desigualdad.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-145-320.jpg)


![1 2 0 • C apítulo 2 • E c u a c io n e s y desigualdades
U S T A Y —1 U tilice si s u e s t a d o civil e s C a s a d o
p o r b ie n e s m a n c o m u n a d o s o v iu d o (a )
Si la cantidad en la
forma 1040, línea 39,
es: mayor que—
Pero no
mayor que—
Escriba la forma 1040,
línea 40
de la cantidad
por encima de—
$0 $45,200 15% $0
45300 109350 $6,780.00 + 27.5% 45,200
109350 166300 24,393.75 + 30.5% 109,250
166,500 297350 41,855.00 + 35.5% 166,500
297,350 88,306.75 + 39.1% 297,350
b) D eterm ine el impuesto q u e deb e pagar una pareja casada p o r bienes m ancom una
dos, si sus ingresos gravables son d e $36,000.
c) D eterm ine el impuesto q u e debe pagar una pareja casada p o r bienes m ancom una
dos, si sus ingresos gravables son d e $136,000.
S o lu c ió n a) Las palabras “Pero no m ayor q u e” significa “m enor q u e o igual a”. Los ingresos
gravables q u e conform an los cinco son:
(0, 45,200] p ara el rango d e 15%
(45,200,109,250] para el rango d e 27.5%
(109,250,166,500] p ara el rango d e 30.5%
(166,500,297350] p ara el rango d e 35.5%
(297350, oo) p ara el rango d e 39.1%
b) E l impuesto q u e deb e pagar una pareja casada p o r bienes m ancom unados con un
ingreso gravable d e $36,000 es 15% d e $36,000. Por lo tanto,
im puesto = 0.15(36,000) = $5400
E l im puesto a pagar es d e $5400.
c) U n ingreso gravable d e $136,000 coloca a la pareja en el rango d e im puestos de
30.5%. E l impuesto es d e $24393.75 + 30.5% del ingreso gravable m ayor a $109,250.
E l ingreso m ayor a $109,250 es $136,000 - $109350 = $26,750. Por lo tanto,
im puesto = 24393.75 + 0.305(26,750) = 24393.75 + 8158.75 = 32352.50
E l im puesto a pagar es d e $32352.50. #
3 R esolver d e sig u a ld a d e s c o m p u e s ta s q u e incluyan “y”
U na desigualdad com puesta está form ada p o r dos desigualdades ligadas con la pala
bra y o la palabra o. E n ocasiones la palabra y está implícita, aunque no esté escrita.
E je m p lo s d e d e s i g u a l d a d e s c o m p u e s t a s
3 < x y x < 5
x + 4 > 3 o 2* - 3 < 6
4* - 6 > - 3 y x - 6< 5](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-148-320.jpg)
![S e cció n 2 .5 • Resolución de de sigualdades lineales * 1 2 1
E J E M P L O 8
Solución
AHORARESUELVAELEJERCICIO 57
E J E M P L O 9
Solución
E n esta parte analizarem os las desigualdades com puestas q u e utilizan o implican
la palabra y. La solución d e una desigualdad com puesta que utiliza la palabra y son todos
los núm eros q u e hacen ambas partes de la desigualdad verdaderas. Por ejem plo, en
3 < x y x < 5
¿cuáles núm eros satisfacen am bas desigualdades? Los núm eros q u e satisfacen am bas
desigualdades pueden determ inarse con facilidad si representam os gráficam ente la so
lución d e cada desigualdad en una recta num érica (vea la figura 2.9). A hora observe
q u e los núm eros q u e satisfacen am bas desigualdades son los núm eros en tre 3 y 5. El
conjunto solución es |*|3 < x < 5).
3 < x ( o x > 3 ) —
- 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
x < 5 « i 1 I 1
- 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
Solución: 3 < x < 5 ■
*
—
I
—I
—I
—I : H K —
F I G U R A 2.9 - 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
Recuerde que, com o se explicó en el capítulo 1, la intersección d e dos conjuntos
es el conjunto d e elem entos com unes a ambos. Para determinarel conjunto solución de
una desigualdad que contenga la palabra y tom e la intersección de los conjuntos solu
ción de las dos desigualdades.
Resuelva * + 2 < 5 y 2 x - 4 > - 2 .
Com ience p o r resolver cada desigualdad p o r separado.
* + 2 < 5 y 2* - 4 > - 2
* < 3 2 x > 2
x > 1
A hora tom e la intersección d e los conjuntos [xx < 3) y xx > 1(.Cuando encontram os
[xx < 3 ) 0 {*1* > 1), determ inam os los valores d e x com unes a am bos conjuntos. La
figura 2.10 ilustra q u e el conjunto solución es |*|1 < * < 3). E n notación d e intervalo,
la solución es (1,3].
- 3 - 2 -1 0 1 2 3 4 5 6 7 8 9
x > i - I ■ í t !
- 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
__ 4 „ Solución: l < x < 3 -M : I ; I 1 !
----- I—
►
FIGURA 2.10 - 3 - 2 -1 0 1 2 3 4 5 6 7 8 9
A veces es posible escribir en una form a más corta las desigualdades com puestas que
utilizan la palabra y. Por ejem plo, podem os escribir 3 < x y x < 5 com o 3 < x < 5. La
p alab ra y no aparece cuando la desigualdad se escribe de esta m anera, pero está
im plícita. L a desigualdad com puesta 1 < * + 5 y * + 5 < 7 puede escribirse com o
1 < x + 5 ^ 7 .
Resuelva 1 < x + 5 < 7.
1 < x + 5 < 7, significa l < A r + 5 y * + 5 ^ 7 . Resuelva cada desigualdad p o r separado.
l < * + 5 y * + 5 < 7
- 4 < x x < 2](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-149-320.jpg)
![1 2 2 • C apítulo 2 • E c u a c io n e s y desigualdades
E JE M P L O 10
Solución
AHORARESUELVAELEJERCICIO 35
E JE M P L O 11
Solución
R ecuerde q u e - 4 < x significa * > - 4 . L a figura 2.11 ilustra q u e el conjunto solución
es |* | - 4 < * < 2). E n notación d e intervalo, la solución es (-4 ,2 ].
-4 < x ( o x > -4)
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
X ^ 2
- 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
Solución: -4 <x*¿2
FIGURA 2.11 -6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6
La desigualdad del ejem plo 9,1 < * + 5 < 7,puede resolverse de o tra forma. Pode
mos seguir utilizando las propiedades analizadas anteriorm ente para resolver desigualda
des compuestas. Sin embargo,cuando trabajamos con tales desigualdades, lo que hagamos
para una parte lo debem os hacer para las tres partes. E n el ejemplo 9 podríam os restar 5
de las tres partes para aislar la variable de enm edio y resolver la desigualdad.
1 < * + 5 =<7
l - 5 < * + 5 - 5 ^ 7 - 5
—4 < * < 2
O bserve q u e ésta es la m ism a solución q u e obtuvim os en el ejem plo 9.
Resuelva la desigualdad - 3 < 2x - 7 < 8.
Queremos aislar la variable *. Comenzamos por sumar 7 a las tres partes de la desigualdad.
- 3 < 2 x - 1 < 8
- 3 + 7 < 2 * - 7 + 7 < 8 + 7
4 < 2 x < 15
A hora divida las tres partes d e la desigualdad en tre 2.
4 2 x 15
— < — < —
2 2 2
15
2 s * < y
L a solución tam bién puede ilustrarse en una recta num érica, escribirse en notación de
intervalo, o presentarse com o un conjunto solución. A continuación m ostram os cada
form a.
f
- 3 - 2 - 1 0 1 2 3 4 5 6 7 8 9
L a respuesta en notación d e intervalo es
{
x
2
sx
<
1í
2 ,- ^ ) . E l conjunto solución es
4 - 3 *
Resuelva la desigualdad - 2 < — - — < 8.
M ultiplique las tres partes p o r 5 p ara elim inar el denom inador.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-150-320.jpg)

![1 2 4 • C apítulo 2 • E c u a c io n e s y desigualdades
400 < 313 + a: < 450
400 - 313 < 313 - 313 + a: < 450 - 313
87 < a: < 137
Moisés necesitaría una calificación mínima d e 87 en su último exam en para obtener una
nota final d e B. Si la calificación más alta q u e se puede alcanzar en el exam en es 100,
¿M oisés podría obtener una nota final d e A (prom edio d e 90 o más)? Explique. #
80 < 3135+ X < 90
4 R e s o lv e r d e s ig u a ld a d e s c o m p u e s ta s q u e in c lu ya n “o ”
L a solución d e una desigualdad com puesta q u e utiliza la palabra o, son todos los nú
m eros q u e hacen verdadera cualquiera de las desigualdades. Por ejemplo, en la desi
gualdad com puesta
x > 3 o x < 5
¿cuáles núm eros satisfacen la desigualdad com puesta? R epresentem os gráficam ente
la solución d e cada desigualdad m ediante la recta num érica (vea la figura 2.12). O b
serve q u e todo núm ero real satisface al m enos una d e las dos desigualdades. Por lo
tanto, el conjunto solución d e la desigualdad com puesta es el conjunto d e todos los
núm eros reales, R.
x > 3 *
x < 5
- 6 - 5 - 4 - 3 - 2 -1 0 1 2 3 4 5 6
- 6 - 5 - 4 - 3 - 2 -1 0 1 2 3 4 5 6
4 Solución: R .....................................................
FIGURA 2.12 -6 - 5 - 4 - 3 -2 -1 0 1 2 3 4 5 6
R ecuerde que, com o se explicó en el capítulo 1, la unión d e dos conjuntos es el
conjunto d e elem entos que pertenecen a cualquiera d e ellos. Para determinar el con
junto solución d e la desigualdad q u e contenga la palabra o y tom e la unión de los
conjuntos solución de las dos desigualdades que conform an la desigualdad compuesta.
E J E M P L O 1 3 R esuelvax + 3 < - l o - 4 x + 3 < - 5 .
Solución Resuelva cada desigualdad p o r separado.
a + 3 - 1 o r
x < - 4
- 4 a
: + 3 < - 5
—4a
: < - 8
a: > 2
A hora represente gráficam ente cada solución en rectas num éricas y después determ i
ne la unión (vea la figura 2.13). L a unión es x < - 4 o x > 2.
x*z - 4 -
FIGURA 2.13
x > 2
Solución: x -4 o x > 2
' 1 1
— 1
— 1
— 1-
- 7 - 6 - 5 - 4 - 3 - 2 - 1 0
-I— 1
— 1
— l
1 2 3 4 5
__1
___1
___1
___1
___1
___1
________ 1
— i — 1—
^1— ■
—^
- 7 - 6 - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5
- 7 - 6 - 5 -4 - 3 - 2 -1 0 1 2 3 4 5
E l conjunto solución es [xx < - 4 ) U{a:|a: > 2), q u e podem os escribir com o [xx < - 4
AHORARESUELVAELEJERCICIO 59 o x > 2). E n notación d e intervalo, la solución es ( - 0 0 , -4 ] U (2,00 ) . #](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-152-320.jpg)

![1 2 6 • Capítulo 2 • E c u a c io n e s y d esigualdades
2L 4<* —2) < 4* - 8 22. 15.3 > 3(a - 1.4)
23. 56 - 6 > 3(6 + 3) + 26 24. - l ( d + 2) < - 9 d + 2(d - 4)
25. | + | £ 4 26. 2y - 6y + 10 £ 2 (-2 y + 3)
Resuelva cada desigualdad y dé la solución en notación de intervalo.
27. 4 + y < 6 28. 4 - 3 * < 7 + 2* + 4
1
m
1
A
l
1
•/•»
1
m
a
30.
6 5 7 ,
2 ~ 6 < S + h
t 4t
3L - - / + 2 < - y + 3 32.
3(* - 2) 5(2 - x)
5 3
« 33. -3 x + 1 < 3[(* + 2) - 2x] - 1 34. 4[x - (3* - 2)] > 3(
Resuelva cada desigualdad y dé la solución en notación de intervalo.
35. - 2 < q + 3 < 4 36. - 7 < p - 5 < -5
37. -1 5 < - 3 z ^ 12 38. -1 6 < 5 - 3n < 10
- 39. 4 < 2x - 4 < 7 40. -1 2 < 3x - 5 < - 4
41. 14 < 2 —3g < 20 42. | < 3* + 4 < 6
Resuelva cada desigualdad y proporcione el conjunto solución.
43. 5 S 3%+ 1 < 11 44.
3 - x - 5 r
~5 < 3 < 6
45. 6 < -3 (2 * - 4) < 12 46.
r 4 - 3 * 2
" 6 < 2 < 3
. 3(M " 4) „
47. 0 < -^ - y — - < 1 48. - 1 5 < 3(7 2 ) , 0
Resuelva cada desigualdad e indique el conjunto solución.
49. c < 2 y e > - 3 50. d > O o d < 5
51. x < 2 y x > 4 52. w < —
1 o te > 5
£ 53. * + 1 < 3 y * + 1 > - 4 54. 5* - 3 < 7 o - x + 3 < - 5
Resuelva cada desigualdad e indique la solución en notación de intervalo.
55. 2s + 3 < 7 o -3 s + 4 < - 1 7 56. 2a + 3 > 7 y -3 a + 4 < -17
5 7 . 4x + 5 > 5 y 3* - 4 < 2 58. 5* - 3 > 10 y 5 - 3* < - 3
59. 4 — x < - 2 o 3 x - 1 < - 1 60. —x + 3 < 0 o 2 x - 5 > 3
6L 2A + 5 > - l y 7 - 3 H 7 62. 2? - 7 < - 3 o 2 - 3? < 11
Resolución de problemas_______________________________________________________
63. Servicio de mensajería Para poder enviar un paquete por b) Un servicio de mensajería definió el término circunfe-
mensajería, es necesario que la suma de su largo más su cir- iencia como eldoble del ancho másel doble del grosor,
conferencia no sea mayor de 130 pulgadas. Escriba una desigualdad que use las variables largo, /,
a) Plantee una desigualdad que exprese esta información; ancho, w , y el grosor, d, para indicar las dimensiones
utilice / para representar el largo y g para la circunfe- permitidas para los paquetes que pueden enviarse por
rencia. mensajería.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-154-320.jpg)


![S e cció n 2 .6 • Resolución d e e c u a c io n e s y desigualdades c o n va lo re s a b so luto s • 1 2 9
L a a s e g u r a d o r a p a g a
0, si c < $100
0.80(c - 100), si $100 < c < $2100
c - 500, si c > $2100
Explique por qué este conjunto de desigualdades descri
be el plan de pago de la aseguradora.
86. Explique por qué no puede despejarse x en la desigual
dad a < b x + c < d , a menos que se proporcione informa
ción adicional
Reto
87. Calificaciones calculadas Las primeras cinco calificacio
nes de RubénAguirre en un curso de historia europea fue
ron 82,90,74, 76 y 68. El examen final del curso cuenta
una tercera parte del promedio final. Un promedio final
mayor que o igual a 80 y menor que 90 daría como resul
tado una nota final de B. ¿Cuál es el rango de calificacio
nesque debe obtener Rubénen el último examen para lo
grar una calificaciónfinal de B? Suponga que la calificación
máxima posible es 100.
En los ejercicios88 a 90, a) explique cómo resolvercada desigualdad, y b) resuelvay proporcione la solución en notación de intervalo.
88. * < 3* - 10 < 2* 90. * + 3 < * + l < 2 . *
89. x < 2 x + 3 < 2 x + 5
Ejercicios de repaso acumulativo
[1 .2 ] 91. Para A = {1,2,6 ,8,9} y B = (1,3,4 ,5 ,8},determine
a) A U B .
b) A D B .
92. Para A = j -3 ,4 , V 7 ,0, - J , liste los ele
mentos que son
a) números para contar.
b) enteros no negativos.
c) números racionales.
d) números reales.
[1.3] Indique el nombre de cada propiedad.
93. (3x + 6) + 4y = 3x + (6 + Ay)
9 4 3x + y = y + 3x
[2.2] 95. Despeje Ven la fórmula R = L + (V — D)r.
2 . 6 R E S O L U C IÓ N D E E C U A C I O N E S Y D E S IG U A L D A D E S
C O N V A L O R E S A B S O L U T O S
a
*
1 E n te n d e r la in te r p re ta c ió n g e o m é tr ic a d e l v a lo r a b s o lu to .
2 R e s o lv e r e c u a c i o n e s d e la f o r m a |x|= a , a > 0.
3 R e s o lv e r d e s ig u a l d a d e s d e la f o r m a |x| < a , a > 0.
4- R e s o lv e r d e s ig u a l d a d e s d e la f o r m a |x| > a , a > 0.
5 R e so lv e r d e s ig u a ld a d e s d e la fo rm a |x| > a o |x| < a , c u a n d o a < 0.
6 R e s o lv e r d e s ig u a l d a d e s d e la f o r m a |x| > 0 o |x| < 0.
7 R e s o lv e r e c u a c i o n e s d e la f o r m a |x| = |y|.
1 Entender la interpretación geométrica del valor absoluto
E n la sección 1.3 se explicó el concepto de valor absoluto. Según se indicó, el valor ab
soluto d e un núm ero puede considerarse com o su distancia (sin signo) respecto del
núm ero 0 en la recta num érica. E l valor absoluto d e 3, escrito |3|, es 3, ya q u e está a 3](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-157-320.jpg)



![S e c c ió n 2 .6 • R e s o lu c ió n d e e c u a c io n e s y d e s ig u a ld a d e s c o n v a lo r e s a b s o lu t o s • 133
4 Resolver desigualdades con la forma |
x
| > a, a > 0
E J E M P L O 6
Solución
E J E M P L O 7
Solución
E J E M P L O 8
A hora veam os las desigualdades con la form a x > a. C onsidere |*| > 3. E sta desi
gualdad representa el conjunto d e valores q u e están a más de 3 unidades d e distan
cia respecto del 0 en la recta num érica (vea la figura 2.14c). E l conjunto solución es
{*1* < - 3 o x > 3). E l conjunto solución p ara |*| > a es el conjunto d e valores q u e
están a m ás distancia que a unidades respecto del 0 en la recta num érica.
Resuelva la desigualdad 2x - 3| > 5 y represente gráficam ente la solución en la rec
ta numérica.
La solución p ara |2* - 3| > 5 es el conjunto d e valores tales que la distancia entre 2x - 3
y 0 en la recta num érica será mayor q u e 5. La cantidad 2x - 3 debe ser m enor q u e - 5 o
mayor que 5 (vea la figura 2.16).
—2 x - 3 —| |—2 x - 3 —
+ r - H — I-i I I I í I I i- - - - - - - - - - - - - - - - Í 1 1 1 ►
FIGURA 2.16- 8 - 7 -6 - 5 - 4 - 3 -2 - 1 0 1 2 3 4 5 6 7 8
Com o 2x - 3 deb e ser m enor q u e - 5 o m ayor q u e 5, establecem os y resolvemos la si
guiente desigualdad com puesta:
2 x - 3 < - 5 o r 2 x - 3 > 5
2 x < —2 2 x > 8
x < - 1 x > 4
- 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 6 7
El conjunto solución p ara 2x - 3| > 5 es {*1* < - 1 o x > 4). C uando x es cualquier
número m enor q u e - 1 o m ayor q u e 4, la expresión 2x - 3 representará un número que
está a m ás d e 5 unidades d e distancia respecto del 0 en la recta num érica (es decir, un
núm ero m enor q u e - 5 o m ayor q u e 5). #
Para resolver desigualdades con la form a |a:| > a,podem os usar el procedim ien
to siguiente.
P a ra re s o lv e r d e s ig u a ld a d e s c o n la fo rm a |x| > a
Si |*| > a y a > O, entonces x < - a o x > a.
Resuelva la desigualdad |2x - 1 1> 7 y represente gráficam ente la solución en la recta
numérica.
C om o esta desigualdad tiene la form a |*| > a , utilizam os el procedim iento q u e se
p lan teó antes.
2 * - 1 < - 7 o r 2* - 1> 7
2 x < - 6 2 * > 8
x < - 3 x > 4
- 6 - 5 - 4 - 3 - 2 - 1 O 1 2 3 4 5 6
Cualquier valor d e x m enor o igual q u e - 3 , o m ayor o igual q u e 4, d aría com o resul
tado q u e 2a: —1 represente un número m ayor o igual q u e 7 unidades d e distancia res
pecto del Oen la recta numérica. El conjunto solución es {a:|a: < - 3 o x > 4). E n notación
d e intervalo, la solución es ( - o o , -3 ] U [4,oo). #
R esuelva la desigualdad
recta numérica.
3 x - 4
> 9 y represente gráficam ente la solución en la](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-161-320.jpg)






![1 4 - 0 • Capítulo 2 • E c u a c io n e s y d esigualdades
Resuelva. Explique cómo determinó su respuesta.
m . x + 1| = 2x - 1 ' 112. |3* + l| = x - 3 ' 113. x - 2 = - ( x - 2)
Reto
Resuelva considerando los signos posibles para x.
114. Ixl + x = 6 115. x + -x = 6 116. x - x = 6 117. x - x = 6
Actividad en equipo
Analice y responda el ejercicio 118 en equipo.
118. Cbnsidere la ecuación x + y = y + x.
a) Cada miembro del equipo seleccione un valor para x y
uno para y, y determine si la ecuación se cumple. Re
pita con otros dos valores para x y y.
b) Determinen en equipo para qué valores de x y y es ver
dadera la ecuación. Expliquen su respuesta.
c) Ahora consideren x - y = -y - x. ¿Bajo qué con
diciones será verdadera esta ecuación?
Ejercicios de repaso acumulativo
(0
Evalúe.
[1.4] 119. J +
120. 4(x + 3y ) - 5xy cuando x = 1, y = 3
[2.4] 121. Natación Raúl Sánchez cruza a nado un lago,pro
mediando 2 millas por hora. Luego da vuelta y re
gresa, promediando esta vez 1.6 millas por hora. Si
el tiempo total de su recorrido es 1.5 horas, ¿cuál es
el ancho del lago?
[2.5] 122. Determine el conjunto solución para la desigualdad
3(x —2) —4(x —3) > 2.
R e s u m e n d e l C A P Í T U L O
Térm inos y frases importantes
2.1 M ínimo com ún múltiplo 2.2 2.4
Coeficiente (o coeficiente (M CM ) Fórm ula Fórm ula d e la distancia
numérico) Térm inos sem ejantes M odelo m atem ático Problem a d e mezcla
Ecuación condicional Ecuaciones lineales con Fórm ula d e interés sim ple Problem a d e movim iento
C onstante una variable Subíndices
Contradicción Simplificar una expresión 2.5
G rado d e un térm ino Conjunto solución 2.3 Y; intersección
Ecuación Soluciones d e una ecua Ángulos com plem entarios D esigualdad com puesta
Ecuaciones equivalentes ción Á ngulos suplem entarios D esigualdad
Identidad Térm inos O; unión
Mínimo com ún Térm inos no sem ejantes O rden (o sentido) d e una
denom inador (M CD) desigualdad
H e c h o s im p o r t a n t e s H f f l l
P r o p i e d a d e s d e la I g u a ld a d
Propiedad reflexiva: a = a.
Propiedad d e sim etría: si a = b, entonces b = a.
Propiedad transitiva; si a =■b y b = c , entonces a = c.
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-168-320.jpg)
![Ejercicios d e re p a so del capítulo * 1 4 . 1
Propiedad d e sum a (o aditiva) a = b , entonces a + c = b + c.
Propiedad d e m ultiplicación (o multiplicativa) d e la igualdad: si a = b ,entonces ac = be; c =h0
Para resolver e cuacio nes lineales
1. E lim ine las fracciones.
2. Simplifique cada lado d e form a separada.
3. Aísle el térm ino con la variable en un lado.
4. D espeje la variable.
5. Com pruebe.
Procedim iento p a ra la resolución d e problem as
1. E n tien d a el problem a.
2. Traduzca el problem a a lenguaje matemático.
3. Realice los cálculos m atem áticos necesarios p ara resolver el problem a.
4. Com pruebe la respuesta obtenida en el paso 3.
5. R esponda la pregunta.
Fórm ula d e distancia Fórm ula d e interés sim ple
distancia = velocidad • tiem po interés = capital • tasa • tiem po
II
o
o i = p rt
P ropiedades usadas para resolver desigualdades
1. Si a > b yentonces a + c > b + c. 4. Si a > b y c > 0, entonces ^
2. Si a > b, entonces a - c > b - c. 5. Si a > b y c < 0, entonces ac < be.
3. S i a > 6 y c > 0 entonces ac > be.
a b
6. Si a > b y e < 0 ,entonces— < —.
V&lor absoluto p a ra a > 0
Si x = a, entonces x = a o x = - a . Si |*| > a, entonces * < - a o x > a.
Si x < a, entonces - a < x < a. Si |*| = |y|, entonces * = y o * = - y .
Ejercicios de repaso del capítulo
[2.1] Indique el grado de cada término.
L 23a3b5 2. 6x 3. - 4 x y ¿
Simplifique cada expresión. Si una expresión no puede simplificarse, especifíquelo.
4. a{a + 3) - 4{a - 1) 5. x2 + 2xy + 6*2 - 4
6. b2 + b - 7 7. 2 [ - ( x - y) + 3x] - 5y+ 6
Resuelva cada ecuación. Si una ecuación no tiene solución, especifíquelo.
8. 5(c + 4) - 2c = ~(c - 4) 9. 3(* + 2) - 6 = 4(* - 5) 10. 3 + ^
l o](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-169-320.jpg)
![1 4 2 • Capítulo 2 • E c u a c io n e s y d esigualdades
U . j( 3 r + 4 ) = j ( 4 r + l ) 12. - 4) = 3 ^x + 13. 3x - 4 = 6x + 4 - 3x
14. 2(x - 6) - 5 - {2x - [4(x - 3) - 5]>
[2.2] Evalúe cada fórmula para los valores dados.
15. m = —— — cuandoy2 = 5, y, = -2 , x2 = -8 , x, = 6
xi x
17. h = + Vq
I + h0cuando a = -32, v0= 0, h0= 80, t = 1
Despeje la variable indicada en cada ecuación.
19. E = IR, para R
2h P = 21 + 2w, para w
23. y = m x + b, para m
25. Rt = Ri + R i + /?3,para/?2
27. K = 2(d + /), para /
/2 .3 J £>i los ejercicios 28 a 32, escriba una ecuación que pue
da utilizarse para resolver cada problema. Resuelva elproble
ma y verifique su respuesta.
28. Venta de calendarios El 1de febrero, un almacén pone a
la venta todos loscalendarios con 75% de descuento sobre
el precio original Si MaríaCristina Solís aprovecha la ofer
ta para comprar un calendario por $5.50, ¿cuál era el pre
cio original del calendario?
29. Aumento poblacional La población de un pequeño pue
blo se incrementa a razón de 350 personas por año. Si la
población actual es de 4750, ¿en cuánto tiempo el pobla
do alcanzará 5800 habitantes?
30. Comisión El salario de DamiánAlcoceres de $300 por se
mana más6% de comisiónpor las ventasque realice. ¿Cuán
todebe vender Damiánpara ganar $650en una semana?
31. Comparación deprecios En el aeropuerto de la ciudad de
Kansas, una empresa ofrece el alquiler de un Ford Focus
por $24.99 diarios con millaje ilimitado. El costo por al
quilar el mismo automóvil en otra compañía es de $19.99
diarios más $0.10 por milla. Si Andrea Ojeda necesita al
quilar un automóvil durante 3 días, determine el número
de millas que necesitaría conducir para que el costo del
alquiler sea igual en ambas compañías
- b + V t)1-4 a c
16. x = — - cuando a = 8, b = 10, c = -3
2 a
18. z = ------—cuando x = 60, p = 64, o = 5, n = 25
<
r
v a
20. A = irr*h, para h
22. A — ~^bh, para h
24. 2x - 3y = 5, para y
^ 3a + b
26. S = — -— , para a
32. Venta En una venta por liquidación, los muebles se venden
con 40% de descuento sobre suprecio normal.Además, a los
artículos con etiqueta verde se lesdescuentan $20 adiciona
les. Si Eduardo Brambila adquirió un artículo con etiqueta
verde y pagó$120,determine cuálera su precio normal.
[2.4] En los ejercicios 33 a 37, resuelva los problemas de mo
vimiento y de mezcla.
33. Inversión en bonos Cuando Gonzalo Brizuela recibió un
bono en el trabajo, invirtió parte del dinero en una cuen
ta del mercado de valores que produce 3.5% de interés
simple, y el resto en un certificado de depósito que pro
duce 4.0% de interés simple. Si la cantidad total de interés
que el señor Brizuela ganódurante el año fue de $187.15,
determine el monto total invertido en cada cuenta.
34. Soluciones defertilizante Enrique Castillo tiene solucio
nes de fertilizante líquido que contienen 20% y 60% de
nitrógeno. ¿Cuántos galones de cada una de estas solucio
nes debe mezclar Enrique para obtener 250 galones de
una solución que contenga 30% de nitrógeno?
35. Dos trenes Dos trenes parten de Portland, Oregón, al mis
mo tiempo y en direcciones opuestas. Un tren viaja a 60
millas por hora y el otro a 90 millas por hora. ¿En cuántas
horas estarán a 400 millas de distancia uno del otro?
36. D-ansbordadores espaciales El transbordador espacial 2
despega 05 hora despuésde que despega el transbordador
espacial 1.Si el transbordador 2 viaja 300 millas por hora
más rápido que el transbordador 1y lo rebasa exactamen
te 5 horas después de haber despegado, determine
a) la velocidad del transbordador espacial 1.
b) la distancia que hay entre el lugar de lanzamiento y
el punto en donde el transbordador 2 rebasa al trans
bordador 1.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-170-320.jpg)
![Ejercicios de re p a so del capítulo • 1 4 3
37. Mezcla de café El señor Santiago Negrete, propietario de
un cafégourmet, vende dos tipos de café, uno a $6.00 la li
bra y el otro a $6.80 la libra. ¿Cuántas libras de cada tipo
de café debe mezclar para producir 40 libras de café que
pueda vender a $6.50 la libra?
de solución al 6% para que la mezcla tenga 12% de solu
ciónde tinte azul?
44. Dos Inversiones Luis Saldaña invierte $12,000 en dos
cuentas de ahorro. Una cuenta paga 10% de interés simple,
yla otra 6% de interés simple.Sien un año Luisganael mis
mo interésen cada cuenta, ¿cuánto invirtió a cada tasa?
45. Centro desalud Elgimnasio Deltoides tiene dos planes de
membresía. Con el primer plan se pagan $40 al mes más un
cargo de $1.00 por visita. El segundo plan exige $25 men
suales más un pago de $4.00 por visita. ¿Cuántas visitas al
mesdebe hacer Eric Mendoza para que le convenga el pri
mer plan?
46. Trenesen Alaska Dos trenes parten de Anchorage al mis
mo tiempo, en vías paralelas, viajando en direcciones
opuestas. El tren más rápido viaja 10 millas por hora más
rápido que el más lento. Determine la velocidad de cada
tren, si entre ambos hay una distancia de 270 millas des
pués de 3 horas.
[2.3, 2 .4 ] Resuelva.
38. Venta de electrónicos El precio de un teléfono inalám
brico se redujo en 20%. Si el precio de venta actual es de
$24,determine el precio original.
39. Trote Nidia Reyes trota cierta distancia; luego da vuelta y
camina de regreso hasta su punto de partida. Mientras trota,
su velocidad promedia 12 millas por hora; al caminar, su
velocidad promedia 2.4 millas por hora. Siel tiempo total
que emplea en su recorrido es de 4 horas, determine
a) el tiempo total que trotó, y
b) ladistancia total que recorrió.
40. Medidas de ángulos Determine las medidas de tres án
gulos de un triángulo si uno de ellos mide 25° más que el
ángulo más pequeño, y el otro ángulo mide 5o menos que
el doble del ángulo más pequeño.
41. Alberca Dos mangueras se utilizan para llenar una alber
ca. La manguera con mayor diámetro suministra 1.5 ve
ces más agua que la de menordiámetro. La manguera más
grande se abre 2 horas antes que la manguera más peque
ña. Si después de 5 horas de haber abierto la primera hay
3150 galones de agua en la alberca, determine la veloci
dad de flujo de cada manguera.
42. Ángulos complementarios Un ángulo complementario
tiene una medida que es 15° menos que el doble de la me
dida del otro ángulo. Determine las medidas de los dos án
gulos.
43. Tinte azul Un fabricante de telas tiene dos soluciones de
tinte azul, ambas hechas con el mismo concentrado. Una
solución tiene 6% de tinte azuly la otra tiene 20%. ¿Cuán
tas onzas de la solución al 20% debe mezclar con 10onzas
[2.5] Resuelva cada desigualdad y responda las preguntas.
Represente gráficamente las soluciones en una recta numérica.
47. 3Z + 7 < 13
48. 5 - 2w > -7
49. 2x + 4 > 9
50. 16 < 4x - 5
4x + 3
51. > - 3
S I 2(x - 3) > 3* + 4
53. - 4(x - 2) > 6x + 8 - 10*](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-171-320.jpg)
![1 4 4 • C apítulo 2 • E c u a c io n e s y desigualdades
Escriba una desigualdad que pueda usarsepara resolver cada problema. Resuelva las desigualdades y responda las preguntas.
55. Límite depeso Una canoa puede transportar de manera
segura un total de 500 libras. Si Joel Bañuelos pesa 180 li
bras, ¿cuál es el número máximo de cajas con 40 libras de
alimento que puede transportar de manera segura en su
canoa?
56. Caseta telefónica Javier Cabrera, un operador telefónico,
feinforma a un cliente que el cargo por realizar una llama
da a Omaha, Nebraska, es de $4.50 por los primeros 3 mi
nutos y 95 centavos por cada minuto o fracción de minu
to adicional. ¿Cuánto tiempo puede hablarel cliente si tie
ne $8.65?
57. Gimnasio Un gimnasio garantiza a sus clientes la pérdida
de peso por un mínimo de 3 libras la primera semana y 1.5
libras cada semana adicional. Determine el tiempo máxi
mo necesario para perder 27 libras.
58. Calificaciones Las primeras cuatro calificaciones de Jaz
mín Alatorre son 94,73,72 y 80. Si para recibir una nota
final de B,es necesario que alcance un promedio final ma
yor que o igual a 80 y menor que 90, ¿qué rango de califi
caciones debe obtener Jazmín en el quinto y último
examen para recibir una B en el curso? Suponga que la
calificación máxima que puede obtener es 100.
Resuelva cada desigualdad. Escriba la solución en notación de intervalo.
59. 1 < * - 4 < 7
6Z - 1 2 < 6 - 3x < - 2
60. 7 < p + 10 < 15
Determine el conjunto solución para cada desigualdad compuesta.
65. h < 2 y Ih - 4 > -25
67. 4* —5 < 11 y - 3 x - 4 > 8
61. 3 < 2x - 4 < 8
64. - 8 < 4 ~ 2X < 0
66. 2 * - l > 5 o 3 * - 2 < 7
68. 7 , 2g < - 5 o - > 1
¡2.5, 2 .6 ] Determine el conjunto solución para cada ecuación o desigualdad.
69. |a| = 2
72. |/ + 5| = 11
75. —2q + 9| < 7
78. |4d - 1| = 6d + 9|
70. |*| < 3
73. |* - 2| > 5
2* - 3
76. = 1
79. 12* - 31 + 4 > -1 0
71. |*| > 4
74. |4 —2*| = 5
* - 4
77. < 6
Resuelva cada desigualdad. Proporcione la solución en notación de intervalo.
80. |3c + 8| - 5 < 2
82. —
6 £ — 7 — < 5
4
84. * - 3 < 4 o 2 * - 5 > 9
8L 3 < 2* - 5 < 9
83. 2p —5 < 7y 9 —3p ^ 12
85. - 1 0 < 3(* - 4) < 12
Examen de práctica del capítulo
1. Diga cuáles el grado del término -4 a1
be*. En los ejercicios 4 a 8, resuelva las ecuaciones.
Simplifique 4 7(¿ + 2) =3 (2d - 4)
2. 2p — 3q + 2pq - 6p{q - 3) - 4p r 2 _ 8
3. lq - {2[3 - 4 (9 + 7)] + 5q] - 6 & 6 + 3 ~ 9](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-172-320.jpg)
![E x a m e n de re p a so a cum u la tivo • 1 4 5
6. - 2 ( x + 3) = 4{3[x - (3* + 7)] + 2}
7. I x - 6(2* - 4) = 3 - (5* - 6)
8. - |( 4 * - 6) = j ( 3 - 6x) + 2
9. Determine el valor de S„ para los valores dados.
1 _ r , fli = 3, r = n = 3
10. Despeje b en c =
n - 36
ÍL Despeje 62en A = —6(6, + 62).
En los ejercicios 12 a 16, escriba una ecuación que pueda usarse
para resolver cada problema. Resuelva las ecuaciones y respon
da las preguntas planteadas.
12. Para jugar al g o lf Determine el costo de un equipo de
palos de golf, sin impuestos, si su costo total incluyendo
7% de impuestos es $668.75.
13.
14
Membresía H precio a pagar para ser miembro de un gim
nasio es de $240 por año más $2 por visita (para el lavado
de toallas y la compra de artículos de tocador). Si Leo
poldo López desea gastar un total de $400 al año en el
gimnasio, ¿cuántas visitas puede hacer?
Paseo en bicicleta Gabriel Fonseca y Roberto Fernández
inician un paseo en bicicleta en el mismo punto, pero en di
recciones opuestas. La velocidad de Gabriel es de 15 millas
por hora,y lade Robertoes de 20 millas por hora. ¿En cuán
tas horas habrá una distancia de 147 millas entre losdos?
15. Solución salina ¿Cuántos litros de soluciónsalina con con
centración de 12% deben añadirse a 10 litros de solución
salina con concentración de 25% para obtener una solu
ción con concentración de 20%?
16. Dos inversiones Juana Blanco tiene $12,000 para invertir,
asíque coloca parte de su dinero en una cuenta de ahorros
que paga 8% de interés simple y el resto en una cuenta de
ahorros que paga el 7% de interés simple. Siel total de in
tereses de las dos cuentas al final de un año es de $910,
determine cuánto dinero invirtióJuana en cada cuenta.
Resuelva cada desigualdad y represente gráficamente las solu
ciones en una recta numérica.
17. 3(2? + 4) < 5(q - 1) + 7
6 - 2 *
18. > - 1 2
Resuelva cada desigualdad y escriba la solución en notación de
intervalo.
19. * - 3 < 4 y 2 * - 4 > 5
20. 1 s < 7
Determine el conjunto soluciónpara las siguientes ecuaciones.
2L |26 + 5| = 9
22. |2x - 3| = - , - 1 0
Determineel conjunto solución para las siguientes desigualdades.
23. |4z -+-12| = 0
24. |2x - 3 1+ 1 > 6
25.
2 * - 3
Examen de repaso acumulativo
Resuelva el examen y verifique sus respuestas con las que apa
recen al final. Revise laspreguntas que haya respondido inco
rrectamente. Los números de la sección y el objetivo en donde
se analiza el material correspondiente se indica después de cada
respuesta.
L Si 4 = {1 ,3,5,7,9,11,13,15} y
B = {2, 3, 5, 7,11,13}, determine
a) A U B .
b) A C B .
2. Indique el nombre de cada propiedad.
a) 4* + y = y + 4*
b) (2*)y = 2(xy)
c) 2(* + 3) = 2* + 6
Resuelva.
3. —
42 + ( -6 )2 - (23 - 2)2
4 ( ftf + ab2 - 3b cuando a
& 8 ~ ^ 2 7 -3 9
|-5 | - [5 - (12 ^ 4)]2
= -1 y 6 = - 2](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-173-320.jpg)
![1 4 6 • Capítulo 2 • E c u a c io n e s y d esigualdades
En los ejercicios 6 y 7, simplifique
6. (2 ,y ) - 2
7.
3mv i Y
v i
8. Comparación de territorios Rhode Island tiene un área
territorial de aproximadamente 1.045 X 103millascuadra
das.Alaska tiene un área territorial de casi 5.704 X105mi
llas cuadradas. ¿Cuántas veces es más grande el área
territorial de Alaska que la de Rhode Island?
En b s ejercicios 9 a 11, resuelva las ecuaciones.
9. - 3 (y + 7) =2 ( - 2 y - 8)
10. 1.2(x - 3) = 2.4* - 4.98
2m 1 4
1L T - 6 = 9 W
12. Explique la diferencia entre una ecuación lineal condicio
nal, una identidad y una ecuación inconsistente. Propor
cione un ejemplo de cada una.
— b + / h 2 —4ac
13. Evalúe la fóimula * = ------- — Para <
*= 3,b =
- 8 y c = —
3.
14 Despeje * de la fórmula y - y = m(x - *j).
15. Resuelva la desigualdad - 4 < ^ < 2 y propor
cione la respuesta:
a) en una recta numérica,
b) como un conjunto solución, y
c) en notaciónde intervalo.
En los ejercicios 16 y 17, determine el conjunto solución.
16. 3h - 1| = 8
17. ¡2* - 4¡ - 6 > 18
18. Serie de béisbol Una semana después de la serie mundial,
una tienda de artículos deportivos marca el precio de to
dos sus mercancías relacionadas con el béisbol con un des
cuento de 40%. Si Martín Garduño compra un bate de
béisbol en $21, ¿cuálera el precio original del bate?
19. Dos automóviles Dos autos parten de Caldwell, Nueva
Jersey, al mismo tiempo viajando en direcciones opuestas.
El auto que viaja hacia el norte se mueve 10 millas por ho
ra más rápido que el autoque viaja hacia el sur.Si entre los
dos autos hay 270 millas de distancia después de 3 horas,
determine la velocidad de cada uno.
20. Mezcla de nueces Mónica Quintero, propietaria de La Ca
sa de las Nueces, tiene castañas que cuestan $6.50 por li
bra y cacahuates que cuestan $2.50 la libra. Si desea
producir 40 libras de una mezcla de castañas y cacahuates
para venderlas a $4.00cada una, ¿cuántas libras de casta
ñas y cuántas de cacahuates debe mezclar?
Respuestas al examen de repaso acumulativo
1 a) {1,2,3,5,7,9,11,13,15) b) p , 5,7,11,13); [Sec. 12, Obj. 4] 2. a) propiedad conmutativa de la adición;
b) propiedad asociativa de la multiplicación; c) propiedad distributiva; [Sec. 1.3, Obj. 6] 3. -15; [Sec. 1.4, Obj. 3]
1 9m i0
4 -6 ; [Sec. 1.4, Obj. 4] 5. 7; [Sec. 1.4, Obj. 3] 6. [Sec. 1.5, Obj. 6] [Sec. 15, Obj. 7] 8. * 545.8 veces;
[Sec. 1.6, Obj. 3] 9. 5; [Sec. 2.1, Obj. 3] 10. 1.15; [Sec. 2.1, Obj. 3] 11. [Sec. 2.1, Obj. 4] 12. La ecuación lineal condicio
nal es verdadera sólo para un valor, una ecuación lineal que es una identidad siempre es verdadera, una ecuación lineal
inconsistente nunca es verdadera; [Sec 2.1, Obj. 5] 13. 3; [Sec 2.2, Obj. 1] 14. * = - — ^ [Sec 2.2, Obj. 2]
15.a) . b) j * | - 2 < x < ! } c) ( - 2 , ! ) ; [Sec.2.5,O bj.3] 16. |-|,3 } ;[S e c .2 .6 ,O b j.2 ]
5
17. {*(* < -1 0 o * > 14); [Sec. 2.6, Obj. 4] 18. $35; [Sec 2.3, Obj. 2] 19. 40 millas por hora, 50 millas por hora;
[Sec. 2.4, Obj. 2] 20. Castañas: 15 libras; cacahuates: 25 libras.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-174-320.jpg)















![Sección 3.2 • F u n cio n e s • 1 6 3
Ejercicios de repaso acumulativo
12.2] 103. Evalúe
- b + V¿>2 -_4ac
2a
para a = 2, b = 7,
y c = -15.
[2.3] 104. Renía de un camión La agencia Renta de Camio
nes cobra una cuota diaria de $60 más $0.10por mi
lla. La agencia Automóviles Nacionales cobra una
cuota diaria de $50 más $0.24 por milla por el mis
mo camión. ¿Qué distancia tendría que conducir
durante un día para que el costo de renta fuera igual
con ambas compañías?
[2.5] 105. Resuelva la desigualdad - 4 <
4 —3*
< 5. Es
criba la solución en notación de construcción de
conjuntos.
[2.6] 106. Determine el conjunto solución para la desigualdad
|3* + 2| > 5.
3 .2 FUNCIONES
1 E n t e n d e r la s r e la c io n e s .
2 R e c o n o c e r f u n c io n e s .
3 U t iliz a r la p r u e b a d e la r e c t a v e r t ic a l.
4- E n t e n d e r la n o t a c ió n d e f u n c io n e s .
5 A p l ic a c io n e s d e f u n c i o n e s e n la v i d a d ia r ia .
1 E n ten d e r las relacio n es
E n la vida diaria, con frecuencia descubrim os relaciones en tre dos cantidades. Por
ejem plo, la cantidad q u e usted gasta al com prar naranjas está relacionada con el nú
mero d e naranjas q u e le entregan a cam bio; la velocidad a la q u e viaja un bote d e ve
la está relacionada con la velocidad del viento; y el im puesto q u e usted paga está
relacionado con los ingresos q u e obtiene.
Suponga q u e las naranjas cuestan 30 centavos cada una. Entonces, una naranja
cuesta 30 centavos, dos naranjas cuestan 60 centavos, tres naranjas cuestan 90 centavos,
y asísucesivamente. Podem os organizar esta inform ación,o relación,com o un conjunto
de pares ordenados, listando prim ero el número de naranjas y luego su costo en centa
vos. E n este caso, los pares ordenados serían (1,30), (2,60), (3,90),etcétera. U na ecua
ción que representa esta situación es c = 30rt,en donde c es el costo en centavos, y n es
el número d e naranjas. Como el costo depende del número de naranjas, decim os q u e el
costo es la variable dependiente y el núm ero d e naranjas es la variable independiente.
A hora pensem os en la ecuación y = 2x + 3. E n ella, el valor obtenido p ara y d e
pende del valor seleccionado p ara x. Por lo tanto, * es la variable independiente y y es la
variable dependiente. O bserve que, a diferencia del caso d e las naranjas,en este ejemplo
no existe una relación física entre * y y. La variable * es la variable independiente y y es
la variable dependiente sim plem ente a consecuencia del lugar que ocupan en la ecuación.
Para una ecuación con las variables * y y,si el valor d e y cfepende del valor d e *,en
tonces y es la variable dependiente y * es la variable independiente. Ya q u e las cantida
des relacionadas pueden representarse como pares ordenados, el concepto de relación
puede definirse como sigue.
DEFINICIÓN U na relación es cualquier conjunto d e pares ordenados.
2 R ec o n o c er fu n cio n es
A continuación analizarem os el concepto d e función, uno d e los m ás im portantes en
matem áticas. U n a función es un tipo especial d e relación en el q u e a cada elem ento de
un conjunto (llamado dom inio) le corresponde exactamente un elem ento de un segundo
conjunto (llam ado rango).](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-191-320.jpg)



![S e cció n 3.2 • F u n cio n e s * 1 6 7
E J E M P L O 4
AHORARESUELVAELEJERCICIO33
E n la gráfica q u e se m uestra en la figura 3.26,
a) ¿qué elem ento del rango form a el p ar de 4 en el dom inio?
b ) ¿qué elem entos del dom inio form an el p ar d e - 2 en el rango?
c) ¿cuál es el dom inio d e la función?
d ) ¿cuál es el rango d e la función?
S o l u c i ó n a) El rango es el conjunto de valores d e y. El valor d e y que tiene como
par el valor d e a: 4 es 3.
b) El dom inio es el conjunto d e valores d e x. Los valores d e x que tienen com o p ar el
valor d e y igual - 2 son 2 y 6.
c) E l dom inio es el conjunto d e valores d e x, del 0 al 7. Por lo tanto, el dom inio es
{a
t|0 £ i s ] | o [0 ,7 ]
d) E l rango es el conjunto d e valores y, d e - 2 a 3. Así, el rango es
{ y ~ 2 ^ y * 3 } o [ - 2 ,3 ] #
E J E M P L O 5 L a figura 3.27 ilustra una gráfica d e velocidad contra tiem po d e un hom bre q u e salió
a cam inar y trotar. E scriba una historia q u e describa el paseo d e este hom bre y q u e
corresponda a esta función.
FIGURA 3.27
I
6
5 - -
4 - -
3 - -
2
1
FI hom bre sale a cam inar y trotar
10 15 20 25
Tiempo (minutos)
30
Solución
AHORARESUELVAELEJERCICIO65
E n t ie n d a e l p r o b le m a El eje horizontal es el tiem po y el eje vertical es la ve
locidad. Cuando la curva es horizontal, significa q u e la persona está trasladándose a la
velocidad constante indicada en el eje vertical. Las rectas casi verticales q u e aum entan
con el tiempo (o q u e tienen una pendiente positiva, com o se estudiará más adelante),
indican un aum ento en la velocidad, m ientras q u e las rectas casi verticales q u e dism i
nuyen con el tiem po (o q u e tienen pendiente negativa), indican una dism inución en la
velocidad.
R e s p o n d a Ésta es una posible interpretación d e la gráfica. E l hom bre cam ina d u
rante más o m enos cinco m inutos a una velocidad d e casi dos millas p o r hora;después,
el hom bre aum enta su velocidad hasta casi cuatro millas p o r hora, y cam ina o tro ta a
esa velocidad durante más o m enos 10 minutos; luego dism inuye su velocidad hasta d e
tenerse, y después descansa durante cinco m inutos;finalm ente, el hom bre aum enta su
velocidad hasta casi cinco millas p o r hora, y trota a esa velocidad durante más o menos
10 minutos. #
4 E n te n d e r la n o ta c ió n d e fu n c io n e s
E n la sección 3.1 graficamos varias ecuaciones, tal com o se resum e en la tabla 3.1. Si
exam ina cada ecuación d e la tabla, verá q u e todas ellas son funciones, ya q u e sus grá
ficas pasan la prueba d e la recta vertical.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-195-320.jpg)










![Ejercicios de repaso acumulativo
Sección 3.3 • F u n cio n e s lineales: gráficas y aplicaciones * 1 7 9
[2.1] 80. Resuelva la ecuación 3x - 2 = ~ ( 3x - 3).
[2.2] 81. Despeje p2de la siguiente fórmula.
E = a ,p , + a2p2 + a3p3
[2.5] 82. Resuelva la desigualdad y (x - 3) > y (3 - x) e
indique la solución a) en la recta numérica; b) en
notación de intervalos, y c) en notación de cons
trucciónde conjuntos.
x - 4
[2.6] 83. Resuelva la ecuación + 2 = 4.
3 . 3 F U N C I O N E S L IN E A L E S : G R Á F IC A S Y A P L IC A C IO N E S
1 Graficar funciones lineales.
2 Graficar funciones lineales usando las intersecciones.
3 Graficar ecuaciones con la form a x = a y y = b .
A Analizar aplicaciones de funciones.
5 Ftesolver de manera gráfica ecuaciones lineales con una variable.
1 G ra fic a r fu n c io n e s lineales
E n la sección 3.1 graficamos ecuaciones lineales. Para graficar la ecuación lineal y = 2x
+ 4, podem os construir una tabla d e valores, determ inar los puntos y trazar la gráfica,
com o se m uestra en la figura 3.32. O bserve q u e está gráfica representa una función, ya
q u e pasa la prueba d e la recta vertical.
X y
-2 0
0 4
1 6
FIGURA 3.32
1— 1_
_ ______|_
_ L ¿.
5
A l y = 7 x + 4
•t
................................ /
i
« - 5 - 4 - 3 - A ~ 1 _ , 2 3 $ ♦
/
i jF * 2
■/ 3 “
/ —A
i
i _c
/
/ - 6
/
Utilizando la notación d e fundones, podem os escribir la ecuación q u e se grafi-
có en la figura 3.32 com o /( * ) = 2x + 4. É ste es un ejem plo d e una fiinción lineal, es
decir, una función con la form a f ( x ) = ax + b. A l graficar cualquier función lineal, se
obtiene una línea recta. El dom inio d e todas las funciones lineales es el conjunto d e nú
m eros reales p ara los q u e la fu n d ó n es un núm ero real; p o r lo tanto, el dom inio de
cualquier función lineal es el conjunto d e todos los núm eros reales, IR: al sustituir x
con cualquier núm ero real en una función lineal, resultará q u e f ( x ) es un núm ero real.
Estudiarem os con más profundidad el tem a dom inios d e funciones en la sección 3.6.
Para graficar una función lineal, tratam os a f ( x ) com o si fuera y y seguimos el
mismo procedim iento utilizado p a ra graficar ecuaciones lineales.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-207-320.jpg)











![Sección 3 .4 • L a fo rm a pendiente intersección de u n a e cu a ció n lineal • 1 9 1
Despeje x en cada ecuación como se hizo en el ejemplo 9. Si cuenta con ella, utilice una calculadora graficadora;de lo contrario trace
la gráfica usted mismo.
65. 3* + 2 = 2x + 3 66. -2 (x - 2) = 3(x + 6) + 1
67. 0.3(* + 5) = -0 .6 (* + 2) 6 8 .2 * + i = 5 * - i
Con ayuda de su calculadora graficadora, localice las intersecciones de los ejes x y y de la gráfica de cada ecuación.
69. y = 2(x + 3.2) 70. 5x - 2y = 7
Tí. ~4x - 3.2y = 8 72. y = j x - -
Ejercicios de repaso acumulativo
[1.4] 73. Evalúe 4{2 - 3[(1 - 4) - 5]} - 2. [2.1] 7 4 R esuelva-y - 3 y = 6(y + 2).
]2.6] En los ejercicios 75 a 77 a ) explique el procedimiento para despejar x en cada ecuación o desigualdad (suponga que b > 0), y
b) resuelva la ecuación o desigualdad.
75. x - a = b
77. x - a > b
76. x - a < b
78. Resuelva la ecuación x - 4 = 2x - 2.
3 . 4 L A F O R M A P E N D IE N T E IN T E R S E C C IÓ N D E U N A E C U A C IÓ N L IN E A L
1 E n te n d e r la tr a s la c ió n d e g rá fic a s .
2 D e te rm in a r la p e n d i e n te d e u n a r e c ta .
3 R e c o n o c e r la p e n d i e n te c o m o u n a r a z ó n d e c a m b io .
4- E sc rib ir e c u a c io n e s lin e a le s e n la f o r m a p e n d i e n te in te r s e c c ió n .
5 G ra fic a r e c u a c i o n e s lin e a le s p o r m e d io d e la p e n d i e n te y la
in te r s e c c ió n d e l e j e y.
6 U s a r la fo rm a p e n d ie n te -in te rs e c c ió n p a r a c o n s tru ir m o d e lo s a
p a rtir d e g rá fic a s .
1 E n te n d e r la tra s la c ió n d e g rá fic a s
E n esta sección estudiarem os la traslación d e gráficas, el concepto d e pendiente, y la
form a pendiente intersección de una ecuación lineal.
Considere estas tres ecuaciones
y = 2 x + 3
y = 2x
y = 2 x - 3
L a gráfica d e cada una d e estas ecuaciones aparece e n la figura 3.50.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-219-320.jpg)












![Ejercicios de repaso acumulativo
S ección 3.5 • L a form a p u nto pendiente de u n a e cu a ció n lineal • 2 0 5
[1.4] 84. Resuelva
- 6 2 - 16 -r 2 -h |—
4|
5 - 3 -2 - 4 - 22
Resuelva cada ecuación.
[2.1] 85. |* + j = | ( * - 2)
86. 2.6* - (-1 .4 * + 3.4) = 6.2
[2.4] 87. Trenes Dos trenes parten de Chicago,Illinois,viajan
do en la misma dirección a lo largo de víasparalelas.
El primer tren sale tres horas antes que el segundo,
y su velocidad es de 15 millas por hora más rápido
que el segundo. Determine la velocidad de cada
tren, si tres horas despuésde que el segundo tren sa
le de Chicago entre ambos trenes hay una distancia
de 270 millas.
[2.6] 88. Resuelva
a) |2* + 1
| > 3, b) |2* + 1
| < 3.
| 3 . 5 L A F O R M A P U N T O P E N D IE N T E D E U N A E C U A C I Ó N L IN E A L
A 1 Entender la form a punto pendiente de una ecuación lineal.
ss 2 Utilizar la form a punto pendiente para construir m odelos a
partir de gráficas.
2 3 Reconocer rectas paralelas y perpendiculares.
1 Entender la forma punto pendiente de una ecuación lineal
E n la sección anterior aprendim os a utilizar la form a pendiente intersección p ara d e
term inar la ecuación d e una recta cuando se conocen su pendiente y su intersección del
eje y. E n esta sección aprendem os a usar la form a punto pendiente para determ inar la
ecuación d e una recta cuando se conocen su pendiente y uno d e sus puntos. L a form a
punto pendiente puede desarrollarse a partir d e la expresión p ara la pendiente en tre
cualesquiera dos puntos (*,y) y (* i,y i) de la recta, com o se m uestra en la figura 3.65.
m =
yi
* - * i
M ultiplicando am bos lados d e la ecuación p o r * - x h obtenem os
y - y, = m (x - x t)
DEFINICIÓN L a form a punto pendiente de una ecuación lineal es
y - y, = m (x - x ,)
en donde m es la pendiente de la recta y (* i,y i) es un punto en la recta.
E J E M P L O 1 Escriba, en la form a pendiente intersección, la ecuación d e la recta q u e pasa p o r el
punto (1,4) y q u e tiene una pendiente d e - 2 .
SoIUC¡Ón Ya q u e se nos dio la pendiente d e la recta y un punto en ella,podem os escribir la ecua
ción en la form a punto pendiente. Entonces podrem os despejar y de la ecuación p ara
escribirla en la form a pendiente intercepción. L a pendiente, m , es - 2 . E l punto en la
recta, (* i,y i),es (1,4). Sustituya m p o r - 2 ,* , p o r 1 y y, p o r 4 en la form a punto p en
diente.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-233-320.jpg)






![212 • C apítulo 3 • Gráficas y funciones
29. y = 2 X + 3
- 2 x + 4y = 8
30. —4x + 6y = 12
2x - 3y = 6
31. x - 3 y = - 9
y = 3x + 6
Determine la ecuación de una recta con las propiedades dadas. Escriba la ecuación en la forma indicada.
« 33. Pasa por (2,5) y es paralela a la gráfica de y = 2x + 4 (for
ma pendiente intersección).
34. Pasa por (-3 ,2 ) y es paralela a la gráfica de 4x - 2y = 6
(forma pendiente intersección).
35. Pasa por (-3 , -5 ) y es paralela a la gráfica de 2x - 5y = 7
(forma general).
36. Pasa por (-1 ,3 ) y es perpendicular a la gráfica de y = -2 x
- 1 (forma general).
37. Cbn intersección del eje x en (3,0) e intersección del eje
yen (0,5) (forma pendiente intersección).
38. Pasa por (-2 , -1 ) y es perpendicular a la gráfica de
— _]_x + j (notaciónde funciones).
39. Pasa por (5, -1 ) y es perpendicular a la gráfica de
y = —.r + 1 (notaciónde funciones).
40. Pasa por (-3 ,4 ) y es perpendicular a la recta con intersec
ción del eje x en (2,0) e intersección del eje y en (0,2)
(forma general).
41. Pasa por (6,2) y es perpendicular a la recta con intersec
ción del eje* en (2,0) e intersección del eje y en (0, -3 )
(forma pendiente intersección).
42. Pasa porel punto (2,1) yes paralela a la recta que pasa por
tos puntos (3,5) y (-2 ,3 ) (notación de funciones).
Resolución de problemas
43. Rutina en una caminadora El número de calorías que se
quemanen una hora de ejercicio en una caminadora es una
función de la velocidad que se emplea. Una persona pro
medio que se ejercita en una caminadora (con una inclina
ción de 0o) a una velocidadde 25 millas por hora, quemará
alrededorde 210calorías.A 6 millas por hora, esta persona
quemará más o menos 370 calorías. Sea C las calorías que
s queman en una hora y s lavelocidad de la caminadora.
a) Determine una función lineal C(s) que se ajuste a los
datos.
b) Calcule las calorías que quema una persona promedio
qercitándose 1 hora en la caminadora a una velocidad
de 5 millas por hora.
44. Caminadora inclinada El número de calorías que se que
man por hora al hacer ejercicio en una caminadora a ve
locidad constante, es una función de la inclinación de la
misma. A 4 mph por hora y con una inclinación de 5o,una
persona promedio quemará 525 calorías; a 4 mph y con
una inclinaciónde 15°,la misma persona quemará 880 calo
rías.Sea C las calorías quemadas y d tos grados de inclina
ciónde la caminadora.
a) Determine una función lineal C(d) que se ajuste a los
datos.
b) Calcule el número de calorías que quema una persona
promedio alejercitarse durante una hora en una camina
dora a 4 millas por hora y con una inclinación de 7o.
45. Demanda de reproductores de D VD La demanda de un
producto se refiere al número de ejemplares de ese pro
ducto que el público estádispuesto a comprar a un precio
dado. Suponga que la demanda, d, de reproductores de
DVD vendidos en un mes es una función lineal del pre
cio,p, para $150 ^ p $400. Siel precio es $200,entonces
se venderán 50 aparatos de DVD por mes. Si el precio es
$300, sólo se venderán 30.
a) Usando los pares ordenados de la forma (p, d), escri
ba una ecuación en que la demanda, d,sea una función
del precio,p.
b) Rjr medio de la función resultante de la parte a), deter
mine la demanda cuando el precio de los reproducto
res de DVD es $260.
c) Itor medio de la función resultante de la parte a), deter
mine el precio de los reproductores de DVD si su de
manda es 45.
46. Demanda decomida rápida El gerente de mercadotecnia
efeun restaurantede comida rápda determinaque lademan
da, d,de una nueva ensalada de pollo es una función lineal
de su precio,p, para $0.80 < p < $4.00.Si el precio es $1.00,
entonces cada mes se venderán530 ensaladas de pollo; siel
precio es $2.00,sólo se venderán 400 ensaladas al mes.
a) Usando los pares ordenados de la forma (p, d), escri
ba una ecuación en que la demanda, d,sea una función
del precio,/?.
b) Itor medio de la función resultante de la parte a), deter
mine la demanda cuando el precio de las ensaladas de
pollo es $1.50.
c) R>rmedio de la función resultante de la parte a),deter
mine el precio de las ensaladas de pollo si su demanda
es 205.
47. Oferta de yo -yo s La oferta de un producto se refiere al
número de ejemplares de ese producto que un vendedor
estádispuesto a vender a un precio dado. La empresa que
fabrica un nuevo tipo de y o -y o para niños determina
que el número de yo-yos que estádispuesta a proveer, s.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-240-320.jpg)


![S e cció n 3 .6 • Á lge b ra d e funcion e s « 2 1 5
Actividad en equipo
57. La siguiente gráfica muestra el crecimiento de la circunfe
rencia de la cabeza de un grupo de niñas. La línea central
representa la circunferencia promedio de la cabeza de
todas las niñas para la edad dada, mientras que las líneas
inferior y superior representan los límites respecto del
rango normal. Analice y responda en equipo las siguientes
preguntas.
a) Explique por qué la gráfica de la circunferencia pro
medio de la cabeza representa una función.
b) ¿Cuál es la variable independiente? ¿Cuál es la varia
ble dependiente?
c) ¿Cuál es el dominio de la gráfica de la circunferencia
promedio de la cabeza? ¿Cuál es el rango?
d) ¿Cuál es el intervalo considerado como normal para
niñas de 18 años?
e) En esta gráfica, ¿la circunferencia de la cabeza es una
funciónde la edad, o la edad es una función de la cir
cunferencia de la cabeza? Explique su respuesta.
f) Calcule la circunferencia promedio de la cabeza de las
niñas a los 10y a los 14 años.
Ejercicios de repaso acumulativo
g) Esta gráfica es casi lineal. Determine una ecuación o
funciónque pueda usarse para calcular la línea central
entre (2,48) y (18,55).
Circunferencia de la cabeza
[2.5] 58. Resuélvala desigualdad4 - x > 2x + 3 e indi
que la soluciónen notaciónde intervalos.
59. Giando ambos lados de una desigualdad se multi
plicano dividen por un número negativo, ¿quédebe
hacer?
[3.2] 60. a) ¿Qué es una relación?
6L
b) ¿Qué es una función?
c) Dibuje una gráfica que represente una relación
pero que no sea una función.
Determine el dominio del rango de la función
{(4,3), (5 ,-2 ),(3 ,2 ) (6,-1)}.
3 . 6 Á L G E B R A D E F U N C IO N E S
a &
1 Determinar la sum a, diferencia, producto y cociente de las
funciones.
2 Representar gráficamente la sum a de funciones.
1 Determinar la suma, diferencia, producto y cociente de las funciones
A continuación analizarem os algunas form as en las q u e se pueden com binar las fun
ciones. Si determ inam os q u e /( * ) = * + 2 y g(x) = x2 + 2xypodem os encontrar /( 5 )
y g(5) com o sigue.
/ ( * ) = x + 2 g ( x ) = x 2 + 2x
/ ( 5 ) = 5 + 2 = 7 g( 5) = 52 + 2 (5 ) = 35
Si sum am os/( * ) + g(x), obtenem os
/ ( * ) + g ( x ) = ( x + 2) + (x2 + 2x)
= x 2 + 3 x + 2
Edad (años)
Fuente:C entro N acional para Esladfelicas d e S alu d d e E stados U n idos](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-243-320.jpg)




![2 2 0 • C apítulo 3 • Gráficas y funciones
a) Calcule la cantidad d e gas natural destinado al uso residencial/com ercial en 2000.
b) Calcule la cantidad d e gas natural destinado al uso industrial en 2000.
c ) Calcule la cantidad d e gas natural destinado al uso en servicio público/transporte
en 2000.
d) Calcule la cantidad total d e gas natural utilizado en 2000.
S o l u c i ó n a) Al leer la gráfica, vemos q u e la cantidad d e gas natural destinado al uso residencial
e n 2000 (indicada p o r el área inferior d e la gráfica) fue d e más o m enos 8 billones de
pies cúbicos.
b) La siguiente área d e la gráfica representa la cantidad d e gas natural destinado al uso
industrial. E n 2000, esta área inicia en 8 billones y term ina aproxim adam ente en 19 b i
llones. L a diferencia en tre estos dos valores, 19 billones- 8 billones, es 11 billones. Por
lo tanto, más o m enos 11 billones d e pies cúbicos d e gas natural fueron destinados al
uso industrial en 2000.
c ) La siguiente área d e la gráfica representa la cantidad d e gas natural destinada al ser
vicio público/transporte. E n 2000, esta área inicia en 19 billones y term ina e n aproxi
m adam ente 39 billones. L a diferencia entre estos dos valores, 39 billones-1 9 billones,
es 20 billones. Por lo tanto, alrededor d e 20 billones d e pies cúbicos de gas natural se
destinaron al uso d e servicio público/transporte en 2000.
d) E n 2000, la cantidad total d e gas natural utilizado en Estados U nidos fue d e casi 39
billones d e pies cúbicos. Esto puede interpretarse directam ente a partir d e la gráfica.
O bserve tam bién q u e 39 billones es el resultado d e sum ar las cantidades determ inadas
E n el ejem plo 4, la cantidad total d e gas natural utilizado en cualquier año es la
sum a del gas natural destinado a las tres categorías. Por ejem plo, si sum am os las res
puestas obtenidas en las partes a), b) y c), obtenem os 8 + 11 + 20 = 39. Así, en 2000
se utilizaron alrededor d e 39 billones d e pies cúbicos d e gas natural. L a línea superior
d e la gráfica m uestra la cantidad total d e gas natural usado.
AHORARESUELVAELEJERCICIO59 en las partes a), b) y c). #
nes. U na m anera d e lograrlo es introducir las funciones d e form a individual. Luego, siguiendo las instrucciones
q u e vienen con su calculadora, puede sum arlas, restarlas, m ultiplicarlas o dividirlas. Por ejem plo, la pan talla de
la figura 3.76 m uestra una T I-8 3 Plus preparada para graficar Y, = x - 3, Y2 = 2x + 4, y la sum a d e las funciones,
Y3 = Y, + Y2. Para obtener Y3 = Y , + Y 2en la T I-8 3 Plus, presione la tecla V A R S ¡. Luego m ueva el cursor a
Y —VARS y seleccione 1: Function. A h o ra presione: Function. A h o ra presione: [ T ] p ara introducir Y ,; luego
presione presione V A R S y vaya a Y -V A R S p ara seleccionar l:Function. Por últim o, presione 2 p ara
introducir Y2. L a figura 3.77 m uestra las gráficas d e las dos funciones y la gráfica d e la sum a d e las funciones.
FIG U R A 3.76 FIG U R A 3.77](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-248-320.jpg)

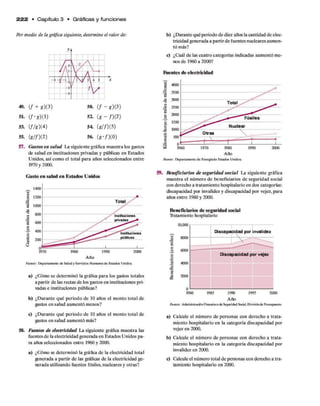

![2 2 4 • Capítulo 3 • Gráficas y funciones
E je rc ic io s d e re p a s o a c u m u la tiv o
[1.5] 72. Evalúe (-3 ) “3. [3.1] 76.Grafique y =|x |- 2.
[1.6] 73. Exprese 1,630,000 en notación científica. [3 3 ] 7?<Grafique 3* - 4y = 12.
[2.2] 74. Despeje h en A = bh.
[2.3] 75. Lavadora El precio de unalavadora, incluyendo
6% de impuesto, es de $477. Determine su precio
sn tomar en cuenta el impuesto.
3 . 7 G R A F IO A C IÓ N D E D E S IG U A L D A D E S L IN E A L E S
fi A
1 Representar gráficamente desigualdades lineales con dos
variables.
1 R e p re s e n ta r g rá fic a m e n te d e s ig u a ld a d e s lineales c o n d o s v a ria b le s
U n a desigualdad lin eal resulta cuando, en una ecuación lineal, el signo d e igual se
reem plaza con un signo d e desigualdad.
Ejem plos de desigualdades lineales co n d o s variables
2 x + 3 y > 2 3 y < 4 x - 6
- x - 2 y < 3 5 x > 2 y - 3
U na recta divide un plano en tres regiones: la recta misma y los dos sem iplanos
uno a cada uno d e sus lados. E n este caso, la recta se denom ina fro n tera. Al graficar la
ecuación lineal 2x + 3y = 6, la recta resultante, llam ada recta frontera, divide el plano
en el conjunto d e puntos q u e satisfacen la desigualdad 2x + 3y < 6 y el conjunto de
puntos q u e satisfacen la desigualdad 2x + 3y > 6. Com o la desigualdad 2x + 3 y < 6
significa 2* + 3 y < 6 o 2 * + 3y = 6,la desigualdad 2x + 3y < 6 contiene a la recta fron
tera. Lo mismo ocurre con la desigualdad 2x + 3y > 6. L a gráfica d e las desigualdades
2 r + 3 y < 6 y 2 * + 3 y > 6 n o contiene la recta frontera. A continuación analizarem os
cóm o graficar desigualdades lineales.
P a ra re p re s e n ta r g rá fic a m e n te u n a d e s ig u a ld a d lineal c o n
d o s va ria b le s
1. Reemplace el símbolo de desigualdad con un signo igual.
2. Trace la gráfica de la ecuación en el paso 1. Si la desigualdad original contiene un símbo
lo > o trace la gráfica utilizando una línea sólida.Si la desigualdad original contiene
un símbolo > o < , trace la gráfica utilizando una línea punteada o discontinua.
3. Seleccione un punto que no esté sobre la línea y determine si éste es una solución de la
desigualdad original. Si el punto seleccionado es una solución, sombree el área de la
gráfica que estédel lado de la línea que contiene este punto. Si el punto seleccionado
no satisface la desigualdad, sombree el área de la gráfica que esté del lado de la línea
que no contiene este punto.
E n el paso 3 decidim os cuál conjunto d e puntos cum ple con la desigualdad dada.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-252-320.jpg)


![Sección 3.7 • G raficación d e d e sigu a ld a d es lineales • 2 2 7
17. 2x - 3y > 12
21. 2x + y < 4
18. 2* + 3y > 6
22. 3* - 4y < 12
^ 19. y < -3 * + 5
23. 10 > 5* - 2y
20. y < - x + 3
2 4 - * - 2 y > 4
Resolución de problemas
m 25. Seguro de vida La tarifa mensual por un segurode vida de
$100,000 para mujeres aumenta de forma casi lineal para
lasedades de 35 a 50. La tarifa para una mujer de 35 años
de edad es de $10.15 al mes,y para una mujerde 50 años es
de $16.45 al mes. Fuente: R.K. Reynolds Insurance Service.
a) Trace una gráfica que se ajuste a estos datos.
b) Marque el área de la gráfica en donde la tarifa es me
nor o igual a $15 al mes.
c) Calcule la edad a la que la tarifa excede, por primera
vez,$15 al mes.
26. índice de Precios al Consumidor El índice de Precios al
Consumidor (IPC) es una medida de la inflacióa Desde
1990, el IPC ha crecido de manera casi lineal. El IPC en
1990 fue de 130.7, y en 2000 el IPC fue de 172.2. Fuente:
Oficina de Censos de Estados Unidos.
a) Trace una gráfica que se ajuste a estos datos.
b) Marque el área de la gráfica en donde el IPC es mayor
que o igual a 150.
c) Calcule el primer añoen el que el IPC fue mayor que
o igual a 150.
27. Remuneraciónpor hora La remuneración por hora es el
monto anual total de los gastos requeridos para emplear
a un individuo, dividido entre el número de horas al año
que éste trabaja. En Estados Unidos, la remuneración pro
medio por hora para todos los empleados ha aumentado
de manera máso menos lineal desde 1975.En ese año,la re
muneración promedio por hora era de $6.36; en 2000, la
remuneración promedio por hora era de $19.86. Fuente:
Oficina de Estadísticas Laborales de Estados Unidos.
a) Trace una gráfica que se ajuste a estos datos.
b) Marque el área de la gráfica en donde la remuneración
promedio por hora es mayorque o igual a $10 por hora.
28.
29.
30.
c) Calcule el primer año en que la remuneración prome
dio por hora excediólos $10 por hora.
7ierras de cultivo en California La cantidad de terreno
de cultivo en California ha disminuido de manera casi li
neal desde 1980. En ese año, California tenía alrededor de
34 millones de acres de tierras de cultivo; en 2000 eran 28
millones de acres. Fuente: Departamento de Agricultura
de Estados Unidos.
a) Trace una gráfica que se ajuste a estos datos.
b) Marque el área de la gráfica en donde la cantidad de
tierras de cultivo es menor que o igual a 30 millones
de acres.
c) Calcule el primer año en que la cantidad de tierras de
cultivo fue menor que o igual a 30 millones de acres.
a) Grafique f(x) = 2x - 4.
b) Marque el área de la gráfica acotada por /(* ), x = 2,
x = 4 y el eje x.
a) Grafique g(x) = —x + 4.
b) Marque el área de la gráfica acotada porg(*),* = 1
y los ejes x y y.
Reto
Grafique cada desigualdad.
3L y < |*| 32. y > x 2
Ejercicios de repaso acumulativo
33. y < x 2 —4
[2.1] 34. Resuelva la ecuación 4 — y - = -6 .
_ (j _
[2.2] 35. Si C = x + Z —^=, determine C cuando * = 80,
V n
Z = 1.96, <r = 3 , y /t = 25.
[2.3] 36. Ofertasmusicales Una tienda de discos está a pun
to de cerrarsus puertas para siempre. La primera se
mana, el precio de todos los artículos se ha reducido
en 10%; la segunda semana se da un descuento adi
cional de $2.Si durante la segunda semana Antonio
Sánchez compra un CD por $12.15, determine el
precio original del CD.
[3.2] 37. /(* ) = - x 1+ 3;determine / ( —
1).
[3.3] 38. Escriba una ecuación de la línea que pasa por el
punto (6, - 2) y es perpendicular a la línea cuya
ecuación es 2x - y = 4.
[3.4] 39. Determine la pendiente de la recta que pasa por
(-4 ,7 ) y (2 ,-1 ).](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-255-320.jpg)

![Ejercicios d e re p a so del capítulo • 2 2 9
O p e r a c i o n e s s o b r e f u n c i o n e s
Suma d e funciones: ( / + g)(*) = f ( x ) + g(x)
D iferencia d e funciones: ( f ~ g ) ( x ) = f ( x ) - g(x)
Producto d e funciones: ( / • g)(*) = /( * ) • g(x)
f ( x )
C ociente d e funciones: { f / g ) ( x ) = , g ( r ) 0
8 x )
Ejercicios de repaso del capítulo
[3.1] 1. Trace los pares ordenados en los mismos ejes.
a) >4(5,3)
Grafique cada ecuación.
1
b) B (0, 4) 0 c (5I ) d ) D ( - 4 ,3 ) e) E (-6 , -1 ) f ) F ( - 2 ,0 )
4. y = 2 * + 3
9. y = |x| - 1
5. y = - ^ x + l
-
10. y = x
3. y = —2x — 1
7. y = x 2 - 1 8. y = |*|
[3.2] 12. Defina qué es una función.
13. ¿Toda relaciónes una función? ¿Toda función es una relación? Explique.
Determine si las siguientes relaciones son funciones;explique sus respuestas.
14. ! 15. {(2,5), (3 ,- 4 ), (5,11), (6 ,- 1 ), (2 ,-5 )}
b 2
c '3
6. y = x 2
11. y = x 3 + 4
En los ejercicios 16 a 19, a ) determine si las gráficas representan funciones; b ) determine el dominio y el rango de cada una.
16. V 17. y
y
4
3
2--
- 4 - 3 - 2 - J
-2
- 3 -
4
3 - -
2--
■ : ; - 4 - 3 - 2 '
—
2--
—
3- -
- 4 - -
3 4](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-257-320.jpg)
![2 3 0 • C apítulo 3 • Gráficas y funciones
20.
2L
22.
Si f ( x ) = - x 2 + 3x - 5, determine
a ) / ( 2 ) y b ) /(/,).
Si g(t) = 2f3 - 3í2 + 1,determine
a ) g ( - l ) y •>) g(a).
Velocidad de un automóvil Jaime González transita a
bordo de un automóvil. La siguiente gráfica muestra la ve
locidad del automóvil como una función del tiempo. Idee
una historia que corresponda a esta gráfica.
2T 7
0
£ 6
0
W 50 +
Ü 20
> 10 +
30
0 5 10 15 20 25
T iem p o (m in u to s)
[3.3] Grafique cada ecuación usando intersecciones.
25. 3x - 4y = 6
Grafique cada ecuación o función.
27. f ( x ) = 4
28. x = -2
29. Compañía derosquillas La utilidad al año,p,de una com
pañía que se dedica a producir rosquillas puede calcularse
por medio de la función p(x) = 0.1* - 5000, en donde x
es el número de rosquillas que se venden al año.
a) Trace una gráfica de utilidades contra rosquillas vendi
das hasta 250,000.
23. Huerto El número de canastas de manzanas, N, que pro
ducen x árboles en un pequeño huerto (x ^ 100),está dado
por la función N(x) = 40.t - O.lx2. ¿Cuántas canastas de
manzanas producen
a) 20 árboles?
b) 50 árboles?
24. M o ta en descenso Siuna pelota se deja caerdesde lo alto
de un edifido de 100 pies, su altura respecto del suelo, h,
en cualquier tiempo, /, puede determinarse por medio de
la función h{t) = -16/2 + 100,0 < t < 2^. Determine la
altura de la pelota
a) 1segundo después de dejarla caer.
b) 2 segundos después de dejarla caer.
26. j x = l y + 20
b ) Calcule el número de rosquillas que deben venderse
para que la compañía alcance el punto de equilibrio
(es decir,que no gane ni pierda).
c) Calcule el número de rosquillas vendidas si la compa
ñía tiene una ganancia de $20,000.
30. Interés Trace una gráfica que ilustre el interés sobre un
préstamode $12,000 por unperiodode un añopara diferen
tes tasas de interés hasta de 20%. Utilice la fórmula interés
= capital • tasa • tiempo.
[3.4] Determine la pendiente y la intersección del eje y de la gráfica representada por cada ecuación.
31* y = 2x “ 3
34 3x + 4y = 10
32. f ( x ) = - 2 x + 1
35. x = - 2
33. 3x + 5y = 12
36. f ( x ) = 6
Determine la pendiente de la recta que pasa por los puntos dados.
37. (2, 5), ( - 2 , 7) 38. (-2 , 3 )(4 ,1)
Determine la pendiente de cada recta. Si la pendiente es indefinida, indíquelo. Luego escriba la ecuación de la recta.
39. y . 40. 41.
A
O.
*-
1—
1
-* - í - -1
1 2 4
-7 -
--
A
—4 — i'A -
7
A
1 . 1 -1—
1
4 - 2 - ? - i i 1 4
—O-
Z
á
— X 'i.
—A
■r](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-258-320.jpg)
![Ejercicios de re p a so del capítulo • 2 3 1
4Z Si la gráfica que se obtiene de y = -2 x + 3 se traslada 4
unidades hacia abajo, determine
a) lapendiente de la gráfica trasladada,
a) la intersección del eje y de la gráfica trasladada,
a) la ecuación de la gráfica trasladada.
43. Si un punto de una gráfica es (-6 , -8 ) y su pendiente es
|, determine la intersección del eje y de la gráfica.
44 Fiebre tifoidea La siguiente tabla muestra el número de
casos reportados de fiebre tifoidea en Estados Unidos pa
ra años seleccionados entre 1970 y 2000.
a) Determine cada punto y trace los segmentos de recta
entre ellos.
b) Calcule la pendiente de los segmentos de recta.
c) ¿Durante qué periodo de diez años el número de casos
reportados de fiebre tifoidea aumentó más?
Año Número de casos de fiebre tifoidea reportados
1970 346
1980 510
1990 552
2000 317
Fuente: Departamento de Salud y Servicios Humanos de
Estados Unidos.
45. Seguridad social La siguiente gráfica muestra el número
de beneficiarios de seguridad social desde 1980,y proyec
tados hasta 2070. Utilice la forma pendiente intersección
para determinar la función n(t) (representada por la línea
recta punteada) que puede usarse para representar estos
datos.
[3.5] Determine si las dos rectas dadas son paralelas, perpendiculares, o ninguna de ellas.
46. 2x - 3y = 10
2 .
y = - x - 4
47. 2x - 3y = 9
-3 * - 2y = 6
48. 4* - 2y = 10
- 2 x + 4y = -8
Determine la ecuación déla recta con laspropiedades indicadas. Escriba sus respuestas en la forma pendiente intersección.
49. Pendiente = —
,pasa por (4,5).
5L Pasa por (0,4) y es paralela a la recta que se obtiene al
graficar y = - j x + 1
53. Pasa por (-3 ,1 ) y es perpendicular a la recta cuya ecua
ción es y = y * + 5
50. P á s a p o r(-3 ,l)y ((2 ,-4 ).
52. Pasa por (2,3) y es paralela a la recta cuya ecuación es 5x
—2y = 7.
54. Pasa por (4,2) y es perpendicular a la recta cuya ecuación
es 4x - 2y = 8.
Se dan dos puntos en l¡ y dos puntos en /2. Determine si /, es paralela a l?, si l¡ es perpendicular al ^ o ninguna de ellas.
55. /,: (4, 3) y (0, - 3 );/2: (1, - 1 ) y (2, -2 )
57. /,: (4,0) y (1,3); fe: (5,2) y(6,3)
59. Tarifas de seguros Las tarifas mensuales por un seguro
de vida de $100,000 para hombres aumenta de manera ca
si lineal de los 35 a los 50 años de edad. La tarifa para un
hombre de 35 años es de $10.76 al mes, y la tarifa para
un hombre de 50 años es de $19.91 al mes. Sea r la tarifa
y a la edad de un hombre entre 35 y 50 años edad.
a) Determine una función lineal r(a) que se ajuste a estos
datos.
b) Utilizando la función resultante de la parte a), calcule
la tarifa mensual para un hombre de 42 añcs de edad.
56. (3,2) y (2, 3); fe: (4 ,1 ) y (1,4)
58. /,: ( -3 ,5 ) y (2,3); h ' (-4 , - 2 ) y (-1 ,2 )
60. Quema decalorías El número de calorías que se queman
al practicar natación durante una hora, cuando se nada a
una velocidad entre 20 y 50 yardas por minuto, es una fun
ción lineal de la velocidad del nadador. Una persona que
nada a 30 yardas por minuto quemará alrededor de 489
calorías en una hora, mientras que nadando a 50 yardas
por minuto quemará más o menos 525 calorías en una ho
ra. Esta información se muestra en la siguiente gráfica.
Beneficiarios de seguridad social](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-259-320.jpg)
![2 3 2 • C apítulo 3 • Gráficas y funciones
Calorías que se queman al nadar
w 600
| 400
cr
200
489
525
0 10 20 30 40 50
Yardas por minuto
Fuem e: H ealth M agazine, sitio W eb w ww .health.com
a) Determine una función lineal que pueda usarse para
calcularel número de calorías,C,que se quemanen una
hora cuando una persona nada a y yardas por minuto.
b) Utilice la función obtenida en la parte a), para deter
minar el número de calorías que se queman en una
hora cuando una persona nada a 40 yardas por minuto.
c) Utilice la función obtenida en la parte a), para deter
minar la velocidad a la que una persona necesita nadar
para quemar 600 calorías en una hora.
[3.6] Dadas f(x) = x1 - 3x + 4 y g(x) = 2x - 5, determine:
6L ( / + g)(*)
62- ( / + *)(3)
(« - /) (* )
64. ( « - / ) ( - 1 )
65. ( f - g ) ( ~ 1)
66. ( f - g ) ( 5)
67. (f/g)( 1)
68- (f/g)(2)
69. Periódicos La siguiente gráfica muestra el número de pe
riódicos que han circulado en Estados Unidos para años
seleccionados entre 1960 y 2000.
Periódicos en Estados Unidos
2000
1500
1000
500
Vespertinos
Matutinos
1960 1970 1980
Año
F uente: A sociación E stadounidense d e Periódicos.
1990 2000
a) Calcule el número de periódicos matutinos que había
en 1 9 6 0 .
b ) Calcule el número de periódicos matutinos que había
en 2000.
c) Calcule el número de periódicos vespertinos que había
en 1 9 6 0 .
d) Calcule el número de periódicos vespertinos que había
en 2000.
e) Calcule el número total de periódicos que había en
1 9 6 0 .
f) Calcule el número total de periódicos que había en
2000.
70. Registros de vehículos automotores La siguiente gráfica
muestra el número de automóviles registrados en todo el
mundo,el número de camiones y autobuses registrados en
todo el mundo, y el número total de vehículos automoto
res registrados en todo el mundo, para años seleccionados
entre 1 9 7 0 y 2 0 0 0 . Sea c el número de automóviles regis
trados y t el número de camiones y autobuses registrados.
Con base en estos datos, calcule:
a) c(2000)
b) í(2000)
c) (c + /)(2000)
Registros de vehículos automotores en el mundo
1970 1980 1990
Año
Füente: Departam ento d e E nergfad e E stados U n id o s
2000
[3.7] Grafique cada desigualdad.
7L y > - 3 71 r < 4
73. y < 4x - 3 74 y < - x - 2](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-260-320.jpg)

![2 3 4 • C apítulo 3 • Gráficas y funciones
manera casi lineal desde más o menos 1970. La siguiente
gráficade barras indica el número de muertes provocadas
por enfermedades cardiacas, por cada 100,000decesos, en
años seleccionados desde 1970.
a) Sea r el número de muertes provocadas por enferme
dades cardiacas por cada 100,000 decesos, y sea t los
años desde 1970. Escriba una función lineal r(t) que
represente esta información.
b) Por medio de la función resultante de la parte a), de
termine el índicede muertes provocadas por enferme
dades cardiacas en 1995.
c) Suponiendo que esta tendencia continúa, determine la
tasa de muertes provocadas por enfermedades cardia
cas en 2010.
índice de m uertes por enfermedades cardiacas
1980 1990
Año
Fuente: Departam ento d e S a lu d y S ervid os H um anos d e Estados Unidos.
En los ejercicios 21 a 23, si / ( x) = 2x2 - x y g(x) = x - 5,
determine:
2 t ( f + g)(3)
22. ( f / g ) ( - 1)
23. f (a)
24 Uso del papel La siguiente gráfica muestra el uso del pa
pel en Estados Unidos en 1995 y el uso del papel proyec
tado de 1995 a 2015.
a) Calcule el número total de toneladas de papel que se
usará en 2010.
b) Calcule el número de toneladas de papel que usarán
las empresas en 2010.
c) Calcule el número de toneladas de papel que se usará
en 2010 en referencias, medios de comunicación im
presos y uso en el hogar.
U so del papel
| 50
40
Referencia, medios de comunicación
impresos y uso en el hogar
1995 2000
fu e n te : C A P V en tures.
25. Grafique y < 3x - 2.
2015
Examen de repaso acumulativo
Resuelvael examen y verifiquesus respuestascon lasque aparecen
d final. Revise laspreguntas que haya respondido incorrectamen
te. Los números de la sección y el objetivo en donde seanaliza el
material correspondiente seindican después de cada respuesta.
L Para A = {1,3,5,7,9} y B = {2,3,5,7,11,13}, determine:
a) A H B.
b) A U S.
2. Cbnsidere el conjunto { - 6 , - 4 , 0 , V3,4.67,” , - V 2 }
Liste los elementos del conjunto que son
a) números naturales.
b) números reales.
3. Evalúe 2 —{3[6 —4(62 4)]}.
Simplifique.
4 ^
y"3
2 * y 2
4xy3
Ingresos municipales En 2001, el monto total de los in
gresos disponibles en cierto municipio fue de $1376 X 109.
La siguiente gráfica muestra un desglose de las fuentes de
ese dinero.
Cobro por —
servicios 15.6%
a) ¿Cuánto dinero se obtuvo a partir de impuestos pre
diales?
b) ¿Cuánto dinero se obtuvo a partir de subvenciones
federales?
c) ¿Cuánto más se obtuvo a partir de impuestos estata
les que a partir de subvenciones estatales?
Origen del dinero
(1576 millones)
Subvenciones t------- 0tras fuentes52%
federales
142%
Impuesto
predial
30.7%
locales 5.0%
Impuesto
Impuestosestatales Subvenciones J?
compartidos 103% estatales 9.4% renta9.6%
Fuente: Departam ento d e Finanzas m u n icp ales d e la ciudad d e Baltimore.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-262-320.jpg)
![R esp ue stas al e xa m e n d e re p a so acum ulativo • 2 3 5
En los ejercicios 7 y 8,resuelva las ecuaciones.
7. 2 (x + 4) - 5 = -3 [ x - {2x + 1)]
9. Simplifique 5* - {4 - [2(x - 4)] - 5}.
10. Despeje b¡ de A = ^ h ( b x + b2).
11. Solucionesdeperóxido dehidrógeno ¿Cuántos galones de
soluciónde peróxido de hidrógeno con una concentración
de 15% deben mezclarse con 10 galones de una solución
del mismo compuesto con concentración de 4% para ob
tener una solución con concentración de 10%?
12. Resuelva la desigualdad 3(* - 4) < 6(2* + 3).
13. Resuelva la desigualdad - 4 < 3x - 7 < 8.
14 Determine el conjunto solución de |3* + 5| = 2x - 10|.
15. Determine el conjunto solución de |2»r —1| < 3.
16. Grafique y = -|% r - 4.
17. a) Determine si la siguiente gráfica representa una fun
ción.
b) Determine el dominio y el rango de la gráfica.
18. Determine la pendiente de la recta que pasa por los pun
tos (-5 ,3 ) y (4,1).
19. Determine si las rectas que resultan al graficar las siguien
tes ecuaciones son paralelas, perpendiculares, o ninguna
de ellas.
2x - 5y = 6
5 x - 2 y = 9
20. Sif(x) =x2+ 3x —2y g(x) =4x - 6 ,determine (f + g)(x).
Respuestas al examen de repaso acumulativo
L a) {3,5,7} b) {1,2, 3, 5, 7, 9,11,13}; [Sec. 1.2, Obj. 4)
Obj.5] 3.92; [Sec. 1.4, Obj. 3] 4 1 6 ^ [Sec. 1.5,Obj. 7]
b) $2.23792 X 108 o $223,792,000 c) $1.4184 x 107 o $1
138
8 . - ^ ; [Sec.2.1, Obj. 4] 9. I x - 7; [Sec. 2.1, Obj. 2] 10
12.* > - r p [Sec.2.5, Obj. 1] 13.1 < * < 5; [Sec. 2.5,0
15. {x| -1 < * < 2}; [Sec.2.6, Obj. 3] 16. y
2
l i l i i i
-6 -4
y = ~ h ~
-6 -
17. a) No es una función b) Dominio: {*1* ^ 2}; rango: (R;
19. Ninguna; [Sec.3.5, Obj. 3] 20. + I x - 8; [Sec.3.6,Ob
2. a) Ninguno b) - 6 , -4 , 0, V 5, 4.67,y , - V 2; [Sec. 1.2,
5.^ j ; [Sec. 15, Obj. 7] 6. a) $4.83832 x 108o $483,832,000
4,184,000; [Sec. 1.5, Obj. 7] 7.0; [Sec. 2.1, Obj. 3]
2A
bx = — - by, [Sec. 2.2, Obj. 2] 11.12 gal; [Sec. 2.4, Obj. 2]
n
bj.3] 14. {-15,1}; [Sec.2.6, Obj. 7]
[Sec.3.1, Obj. 2]
—
M—
1
----1
2 x
1
Sec. 3.2, Obj. 3] 18. [Sec. 3.4,Obj. 2]
j l ]](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-263-320.jpg)












![Ejercicios de repaso acumulativo
Sección 4 .2 • Resolución d e sistem as d e e cu a cio n e s c o n tre s variables • 2 4 9
[1.2] 102. Explique la diferencia entre un número racional y
uno irracional.
[1.2] 103. a) ¿Todos los números racionales son números
reales?
b) ¿Todos los números irracionales son números
reales?
[2.1] 104. Resuelva la ecuación ^-(x - 7) = ^ ( 2 x + 1).
[22] 105. Encuentre todos los números talesque x - 4| = |4 - *|.
[2.2] 106. Evalúe A = p ^ l + -cuando p = 500,r = 0.08,
n = 2 y t = 1.
• [3.5] 107. ¿La relación {(-3,4), (7,2),(-4,5),(5,0),(-3,2)}
es una función? Explique su respuesta.
[3.6] 108. Sea f(x) = x + 3 y g(x) = x2 - 9. Determine
(ffgX3).
4 . 2 R E S O L U C IÓ N D E S IS T E M A S D E E C U A C I O N E S C O N T R E S V A R IA B L E S
1 Resolver sistemas de ecuaciones con tres variables.
2 Aprender a interpretar geom étricam ente un sistema de ecua
ciones con tres variables.
3 Reconocer sistemas inconsistentes y dependientes.
1 R e s o lv e r s is te m a s d e e c u a c io n e s c o n tre s v a ria b le s
La ecuación 2 x - 3 y + 4 z = 8 es un ejemplo de una ecuación linealcon tres variables. La
solución de este tipo de ecuaciones lineales es una tem a ordenada de la forma (x ,y ,z ).
Una solución para la ecuación dada es (1,2,3). Compruébelo.
Para resolversistemasde ecuaciones linealescon tres variables,podemos usar los
métodos de sustitución o de la suma que analizamos en la sección 4.1.
E J E M P L O 1 Resuelva el siguiente sistema por sustitución.
* = - 3
3 x + 4 y = 7
- 2 x - 3 y + 5 z = 19
Solución Como sabemos que x = - 3 ,sustituimos x por -3 en la ecuación 3 x + 4 y = 7, y des
pejamos y.
3 x + 4 y = 7
3(—
3) + 4 y = 1
- 9 + 4 y = 1
4y = 16
y = 4
Ahora sustituimos x = - 3 y y = 4 en la última ecuación,y despejamos z.
- 2 x - 3 y + 5 z = 19
- 2 ( -3 ) - 3(4) + 5z = 19
6 - 12 + 5z = 19
- 6 + 5z = 19
5z = 25
z = 5](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-277-320.jpg)
![2 5 0 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
AHORA RESUELVA EL E JE R C IC IO 3
E J E M P L O 2
Solución
Comprobación x = - 3 , y = 4 , z = 5. L a solución debe verificarse en las tres ecua
ciones originales.
x = - 3 3 x + 4y = 7 - 2 x - 3 y + 5 z = 19
- 3 = - 3 3 ( - 3 ) + 4 (4) = 7 —
2 ( - 3 ) - 3 (4) + 5(5) = 19
7 = 7 Verdadero 19 = 19 Verdadero
L a solución es la terna ordenada (-3 ,4 ,5 ). R ecuerde q u e la tem a ordenada lista pri
m ero el valor a, después el valor y y p o r último el valor z. #
No todos los sistem as lineales con tres variables pueden resolverse p o r sustitu
ción d e form a tan directa com o en el ejem plo 1. Cuando un sistem a d e tercer orden no
puede resolverse fácilm ente p o r sustitución, podem os encontrar la solución utilizan
do el m étodo d e la sum a, com o se ilustra en el ejem plo 2 .
Resuelva el siguiente sistem a d e ecuaciones m ediante el m étodo d e la suma.
3 a + 2y + z = 4 (ec. 1)
2 a - 3y + 2 z = - 7 (ec. 2)
a + 4y - z = 10 (ec. 3)
Para resolver este sistem a d e ecuaciones, debem os o b ten er prim ero dos ecuaciones
con las mismas dos variables. Esto se hace eligiendo dos ecuaciones y utilizando el m é
todo d e la sum a p ara elim inar una d e las variables. Por ejem plo, sum ando la (ec. 1) y
la (ec. 3) elim inam os la variable z. D espués utilizamos un p ar diferente d e ecuaciones
[ya sea (ec. 1) y (ec. 2) o (ec. 2) y (ec. 3)] y em pleam os el m étodo d e la sum a p ara eli
m inar la m ism a variable q u e fue elim inada con anterioridad. Si multiplicam os (ec. 1)
po r - 2 y la sum am os a (ec. 2), la variable z será elim inada nuevam ente. E ntonces ten
drem os dos ecuaciones con sólo dos incógnitas. Comencemos p o r sum ar (ec. 1) y (ec. 3).
3a + 2y + z = 4 (ec. 1)
a + 4y - z = 10 (ec. 3)
4 a + 6y = 1 4 Suma de las ecuaciones, (ec. 4).
U tilicem os ahora un conjunto diferen te d e ecuaciones y elim inem os d e nuevo la
variable z.
- 6 a - 4 y - 2z = - 8 (ec. 1) Multiplicada por -2 .
2a - 3 y + 2z = - 7 (ec. 2)
_ 4a — 7 y = —15 Suma de las ecuaciones, (ec. 5).
A hora tenem os un sistem a d e dos ecuaciones co n dos incógnitas, (ec. 4) y (ec. 5). Si
sum am os estas dos ecuaciones, elim inarem os la variable a.
4a + 6 y = 14 (ec. 4)
- 4 a ~ 7 y = - 1 5 (ec. 5)
—y = —1 Suma de las ecuaciones,
y = 1
Luego sustituim os y = 1 en cualquiera d e las dos ecuaciones con sólo dos variables
[(ec. 4) o (ec. 5)] y despejam os a.
4a + 6y = 14 (ec. 4)
4a + 6 (1) = 14 Sustituya y por! en la (ec. A).
4 a + 6 = 14
4 a = 8
a = 2](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-278-320.jpg)





![2 5 6 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
Reto
Determine la soluciónpara los siguientes sistemas de ecuaciones.
49. 3p + 4q = 11 50. 3a + 2b - c = 0
2p + r + s = 9 2a + 2c + d = 5
q - s = -2 a + 2b - d = -2
p + 2q - r = 2 2 a - b + c + d = 2
Ejercicios de repaso acumulativo
[2.2] 51. Esquí a campo traviesa Margarita Suárez empieza
a esquiar a 3 millas por hora. Diez minutos después,
hora),su esposo, David, comienza a esquiar por
el mismo camino a cinco 5 por hora.
a) ¿Cuáito tiempo despuésde que Davidcomienza
a esquiar alcanzará a Margarita?
b) ¿A qué distancia desde el punto inicial se en
contrarán?
[2.6] Determine cada conjunto solución.
2x 3* - 4 1
S I
4 ~ T
> 5 53.
2 - 1 < 5 54
^2
= -5
4 - 3 S IS T E M A S D E E C U A C I O N E S L IN E A L E S : A P L IC A C IO N E S Y R E S O L U C IÓ N
D E P R O B L E M A S
1 Utilizar sistemas de ecuaciones para resolver problem as de
aplicación.
2 Utilizar sistemas lineales con tres variables para resolver
problemas de aplicación.
1 U tiliza r s is te m a s d e e c u a c io n e s p a ra re s o lv e r p ro b le m a s d e a p lic a c ió n
M uchos d e los problem as d e aplicación q u e se resolvieron e n capítulos anteriores usan
do una sola variable pueden resolverse usando dos variables. E n seguida se presentan
algunos ejem plos q u e m uestran cómo pueden describirse los problem as d e aplicación
m ediante sistem as d e ecuaciones.
EJ E M PLO 1 Cam bios en la fuerza d e trab a jo L a gráfica d e la figura 4.6 in
dica que,en Estados Unidos, el porcentaje d e hom bres en la fuerza d e trabajo está dis
m inuyendo d e m anera constante, m ientras q u e el p orcentaje d e m ujeres está
aum entando gradualmente. La función m (t) = -0.251 + 85.4, en donde t = años desde
1955, puede usarse p ara calcular el porcentaje de hom bres q u e participa en la fuerza
d e trabajo,y la función w(t) = 0.521 + 35.7 puede usarse p ara calcular el porcentaje de
mujeres. Si esta tendencia continúa,determ ine en qué año el porcentaje d e mujeres que
participa en la fuerza d e trabajo será igual al porcentaje d e hombres.
Solución E n tie n d a e l p r o b le m a y tr a d u z c a C onsidere las dos funciones
d adas anteriorm ente com o el sistem a d e ecuaciones. P ara determ inar en q u é año el
porcentaje d e m ujeres será igual al porcentaje d e hom bres,podem os establecer las dos
funciones d e tal m anera q u e sean iguales, y despejar el tiem po, t.
Mujeres y hombres en
la fuerza de trabajo
(Porcentaje de población en
la fuerza de trabajo civil)
Año
Fuenle: Departam ento d e Trabajo d e
E stados Unidos.
FIGURA 4.6](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-284-320.jpg)












![Actividad en equipo_________________________
2 7 0 • C apítulo 4 • Sistem as de e cu a cio n e s y desigualdades
Analicen y respondan en equipo el ejercicio 55.
55. Dos automóviles Un sistema no lineal de ecuaciones es
aquel que contiene al menos una ecuación que no es li
neal. (Los sistemas no lineales de ecuaciones se estudiarán
en el capítulo 10). La gráfica muestra un sistema no lineal
de ecuaciones. Las curvas representan velocidad contra
tiempo para dos automóviles.
a) ¿Las dos curvas son funciones? Expliquen.
b) Analicen el significado de esta gráfica.
c) En el momento t = 0.5 h, ¿cuálde los automóviles está
viajando a mayor velocidad? Expliquen su respuesta.
d) Supongan que los dos automóviles inician en la misma
posición y viajan en la misma dirección. ¿Cuál auto
móvil,A o B, viaja más lejos en una hora? Expliquen
su respuesta.
Tiempo (horas)
Ejercicios de repaso acumulativo
[1.4] 56. Evalúe x + x y + y cuando x = - 2 , y = 5.
57. Resuelva 4 - 2[(x - 5) + 2x] = ~(x + 6).
58. Explique cómo determinar si una gráfica represen
ta una función.
59. Escriba una ecuación para la recta que pasa por los
puntos (6, -4 ) y (2, -8).
I 4 . 4 R E S O L U C IÓ N D E S IS T E M A S D E E C U A C I O N E S P O R M E D IO D E M A T R IC E S
1 Escribir una m atriz aum entada.
é k
2 Resolver sistemas de ecuaciones lineales.
3 Resolver sistemas de ecuaciones lineales con tres variables.
f t
a Reconocer sistemas inconsistentes y sistemas dependientes.
1 Escribir una matriz aumentada
U n a m atriz es un arreglo rectangular d e núm eros dentro d e corchetes. E jem plos de
m atrices son
"4 ó l [ 5 7 2 1
9 - 2 j [ - 1 3 4 j
Los núm eros dentro d e los corchetes se denom inan elem entos de la matriz.
La m atriz d e la izquierda contiene 2 filas y 2 colum nas; p o r lo tanto, se le llama
matriz d e 2 p o r 2 (2 X 2). L a matriz d e la derecha contiene 2 filas y 3 columnas; p o r lo
tanto,es una m atriz d e 2 p o r 3 (2 X 3). Al escribir las dim ensiones d e una m atriz, siem
p re se indican prim ero las filas y luego las colum nas d e q u e consta. U na m atriz cuadra
da tiene el mismo número d e filas q u e d e columnas. Así, la matriz d e la izquierda es una
matriz cuadrada.
E n esta sección utilizarem os m atrices p ara resolver sistem as d e ecuaciones li
neales. Para ello, prim ero hay q u e escribir cada ecuación en la form a ax + b y = c. El](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-298-320.jpg)
![Sección 4 .4 • R esolución d e sistem as de e cu a cio n e s p o r m edio d e m atrices • 2 7 1
siguientepasoconsisteenescribir lamatrizaumentada,esdecir,unamatriz conform a
da por dos matricespequeñasseparadas por una barravertical. Los números a la
izquierdade lalíneaverticalsonloscoeficientesde lasvariablesdelsistemadeecua
ciones,y losnúmeros aladerechasonlasconstantes. Parael sistemadeecuaciones
a xx + b xy = ci
a2x + b2y = c2
lamatrizaumentadaseescribe
a x bi
c
'l
_a2 ¿2
c
J
A continuacióntenemosunsistemadeecuacionesy sumatriz aumentada.
Sistem a de e cuacio nes M atriz aum entada
- * + 2 y = 4
■3*
1 2
-3 -5
Observequelabarraverticalde lamatriz aumentadaseparaloscoeficientesnuméri
cosde lasconstantes. Como lamatrizessólo unaformaabreviadadeescribirelsiste
made ecuaciones, podemos resolver un sistema lineal utilizando matricesde una
manerasimilar acomo lohacemosmedianteel métodode lasuma.
2 R e s o lv e r s is te m a s d e e c u a c io n e s lineales
Pararesolverunsistemadedosecuacioneslinealesmediantematrices,reescribimosla
matriz aumentadaen form a triangular,
IkJ:]
endondea, p y q sonconstantes. A partir deestetipo de matriz aumentadapode
mosescribir unsistemadeecuacionesequivalente. Esta matriz representaal siste
malineal
1x + ay = p
Ox + 1y = q
x + ay = p
y = q
Porejemplo,
1 3
0 1
representa
* + 3y = 4
y = 2
Observequeelsistemadel ladoderechopuederesolversefácilmenteporsustitución.
Susoluciónes(-2,2).
Parareescribir lamatrizaumentadaenformatriangular,utilizamostransform a
ciones d e fila, mismasquepuedenrealizarsemediantetresprocedimientos.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-299-320.jpg)
![2 7 2 • C apítulo 4 • Sistem as de e cu a cio n e s y desigualdades
E J E M P L O 1
Solución
P rocedim ientos p a ra la transform ación d e filas
L Todos los números de una fila pueden multiplicarse por (o dividirse entre) cualquier
número real distinto de cero. (Esto es lo mismo que multiplicar ambos lados de una
ecuaciónpor un número real distinto de cero).
2. Todos los números de una fila pueden multiplicarse por cualquier número real distinto
de cero. Los productos resultantes pueden sumarse a los números correspondientes en
cualquier otra fila. (Esto es equivalente a eliminar una variable del sistema de ecuacio
nes utilizando el método de la suma).
3. Dos filas de una matriz pueden intercambiarse. (Esto es b mismo que intercambiar
dos ecuaciones en el sistema de ecuaciones).
Por logeneral, al cambiar unelementode lamatriz aumentadapor 1seutiliza
elprimerodelosprocedimientosdescritos,y alcambiarunode loselementospor0uti
lizamoselsegundoprocedimiento.Se trabaja por columnas,comenzando por la de la
izquierda;enotraspalabras,inicieconlaprimerafilade laprimeracolumna.
Resuelvaelsiguientesistemadeecuacionesutilizando matrices.
2 x - 3 y = 10
2 x + 2 y = 5
Primeroescribimos lamatriz aumentada.
2 -3
2 2
10
Nuestroobjetivoesobtener unamatrizdelaforma
[kJ:].Paraello,comenza
mospor utilizarel procedimiento 1delastransformacionesdefilaparacambiar el 2
en laprimerafilade laprimeracolumnapor 1. Parahacerlo,multiplicamoslaprime
rafilade númerospor1. (Abreviamosestamultiplicacióncomo R Xy colocamosla
expresiónaladerechadelamatriz,en lamismafilaendondese realizó laoperación.
Estopuedeayudarleaseguir elprocedimientoconmásclaridad).
Conestoseobtiene
2 (1 ) -3 (1
2 2
10(¿
5
i - i
El paso siguienteesobtener 0 en lasegundafilade laprimera columna,dondepor
el momentoseencuentraun2. Lo haremosmultiplicando por-2 los númerosdela
primerafila,y sumamoslosproductosalosnúmerosde lasegundafila. (Esto seabre
via - 2 R X + R2).
Losnúmerosde laprimerafila,multiplicadospor -2 son
l(-2 ) - - ( - 2 ) 5(-2)
Ahorasumamosestosproductosasusnúmerosrespectivosdelasegundafila. Cones
toobtenemos
2 + l(-2 ) 2 + ( - f ) ( - 2 ) 5 + 5(-2) -2 R, + R-](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-300-320.jpg)
![Sección 4 .4 • Resolución d e sistem as d e e c u a c io n e s p o r m edio de m atrices • 2 7 3
A hora tenem os
1 " I
0 5
5
Para obtener 1 en la segunda fila d e la segunda colum na, multiplicam os la segunda fi
la d e núm eros p o rj.
so) i -5(i;
[M I 4]
L a m atriz se encuentra ahora en la form a q u e buscábamos. E l sistem a d e ecuaciones
triangular equivalente es
3 .
* " 2 :V = 5
y = - i
A hora podem os despejar * m ediante sustitución.
* - y = 5
* - | ( - D = 5
* + 2 = 5
7
X = 2
AHORARESUELVAELEJERCICI019 Com pruebe q u e la solución del sistem a es ( | , —1).
3 R e s o lv e r s is te m a s d e e c u a c io n e s lineales c o n tre s v a ria b le s
A hora utilizaremos las matrices p ara resolver un sistema d e tres ecuaciones lineales con
tres variables. Usarem os el mismo procedim iento d e transform aciones d e filas q u e em
pleam os para resolver un sistem a d e dos ecuaciones lineales. N uestro objetivo es o b
tener una m atriz aum entada en form a triangular
P
<
i1
r _
donde a, b , c , p yq y r son constantes. E sta m atriz representa el siguiente sistem a de
ecuaciones.
1x + a y + b z = p x + a y + b z = p
0* + 1y + cz = q o y + c z = q
Ox + Oy + i z = r z = r
Al construir una matriz aum entada, trabajep o r columnas, com enzando p o r la del
extremo izquierdo y finalizando con la del extremo derecho. Siempre termine las ope
raciones en una colum na antes de pasar a la siguiente. E n cada colum na, prim ero ob-](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-301-320.jpg)


![2 7 6 • Capítulo 4 • Sistemas de ecuaciones y desigualdades
4 R e c o n o c e r s is te m a s in c o n s is te n te s y s is te m a s d e p e n d ie n te s
Al resolver un sistem a d e dos ecuaciones, si usted obtiene una m atriz aum entada en
la q u e todos los núm eros d e una fila al lado d e la barra vertical son ceros, pero no hay
ceros q u e les correspondan en el o tro lado, significa q u e el sistem a es inconsistente y
no tiene solución. Por ejemplo, un sistem a d e ecuaciones con el q u e se obtiene la si
guiente m atriz aum entada es un sistem a inconsistente.
Sistema inconsistente.
L a segunda fila d e la m atriz representa la ecuación
Ox + O y = 4
qu e nunca es verdadera.
Si obtiene una matriz con ceros en toda una fila, el sistem a d e ecuaciones es d e
pendiente. Por ejemplo, un sistem a d e ecuaciones q u e produce la siguiente m atriz au
m entada es un sistem a dependiente.
I - 3 -2~|
) 0 0 I «----------Sistema dependiente.
L a segunda fila d e la m atriz representa la ecuación
Ox + Qy = 0
qu e siem pre es verdadera.
Los sistem as d e ecuaciones con tres ecuaciones cum plen reglas similares.
Sistema inconsistente.
AHORARESUELVAELEJERCICIO27
" l 2 4 5"
0 0 0 - 1
_0 1 - 2 3_
" l 3 - 1 2~
0 0 0 0
_0 4 1 - 3 _
Sistema dependiente.
30 C ó m o utilizar su ca lcu la d ora g ra fica d o ra
M uchas calculadoras graficadoras p u ed en trab ajar con m atrices y realizar operaciones en las filas. Por
consiguiente, estas calculadoras graficadoras pueden utilizarse p ara resolver sistem as d e ecuaciones m ediante
matrices.
Lea el m anual d e instrucciones q u e viene con su calculadora graficadora p ara ver si puede m anipular m atri
ces. Si es así, aprenda a utilizarla p ara resolver sistem as d e ecuaciones m ediante matrices.
C o n j u n t o d e e j e r c i c i o s 4 . 4
Ejercicios conceptuales
L ¿Qué es una matriz cuadrada?
2. Explique cómo construir una matriz aumentada.
3. Si usted obtiene esta matriz aumentada al resolver un
sistema de ecuaciones, ¿cuál sería el siguiente paso para
completar el procedimiento? Explique.
1 3 I ó ]
0 - 1 4](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-304-320.jpg)


![Se cció n 4 .5 • Resolución d e sistem as d e e c u a c io n e s por m edio d e d e term inantes... • 2 7 9
52. Navegadores Web La siguiente gráfica muestra que en
2002, Microsoft y Netscape controlaron la mayorparte del
mercado de navegadores Web. Microsoft controló alrede
dor de 49% más mercado que Netscape, y Netscape con
troló alrededor de ocho veces la cantidad que controlaban
todos los demás productores de este tipo de programas.
Determine el porcentaje que corresponde a cada sector
de la gráfica que se muestra.
Ejercicios de repaso acumulativo
Distribución del mercado de navegadores Web
Otras
Netscape
Microsoft
Fuente: www.wcbrcvlew.ccm
[1.2] 53. A = (1,2,4,6,9}; B = {3,4,5,6,10}. Determine
a ) á U 8 ;
b) A n B.
[2.5] 54. Indique la desigualdad - 2 < x < 4
a) en una recta numérica,
b) como un conjunto solución, y
c) en notaciónde intervalo.
[3.2] 55. ¿Qué representa una gráfica?
[3.4] 56. 56.Si/(a:) = - I x 2 + 4x - 6, determ ine/(-5).
4 . 5 R E S O L U C IÓ N D E S IS T E M A S D E E C U A C I O N E S P O R M E D IO D E
D E T E R M I N A N T E S Y L A R E G L A D E C R A M E R
a f e
1 Evaluar un determinante de una matriz 2 x 2 .
2 Utilizar la regla de Cramer.
3 Evaluar un determinante de una matriz 3 x 3 .
4 Utilizar la regla de Cram er con sistemas de tres variables.
1 Evaluar un determinante de una matriz 2 x 2
Hemosestudiadovariosmétodospararesolversistemasdeecuacioneslineales:grafi-
cación,sustitución,el métodode lasuma(o eliminación) y m
atrices. Los sistemasde
ecuaciones linealestambiénpuedenresolversemediantedeterminantes.
Todaslasmatricescuadradastienenunnúmeroasociadoqueseconocecomosu
determinante. Enelcasodeunamatrizde2 X 2,eldeterminantesedefinecomosigue.
D E F IN IC IÓ N
El determinante de una matrizde 2 X 2
evalúacomo
a M
, sedenotapor
_a2 b2J
a x bx
a2 ¿>2
y se
a x bx
a2 bi
= abi ~ a2bx
E J E M P L O 1 Evalúecadadeterminante.
2 - 1
a) 3 5
Solución a) a ¡ = 2 , a 2 = 3yb, = -1 yb2 = 5
b)
-2 3
-1 4
2 x _ 1
3 5
= 2 (5) - (3 )(—1) = 10 + 3 = 13](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-307-320.jpg)


![2 8 2 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
E J E M P L O 3
S o lu c ió n
terminantemenorde Losdeterminantesmenoresde losdemáselementosseloca
lizandemanerasimilar.
b¿ c 2
bi c3
Determinante menorde a,.
b Ci
bi c3
Determinante menorde a2-
bx c,
b i c 2
Determinante menorde a3.
Paraevaluar losdeterminantesde unamatriz de3 X 3,utilizamoslosdeterminan
tes menores. En el siguiente recuadro semuestracómo evaluarlospor el desarrollo
d e m enores delaprimeracolumna.
Desarrollo d e los dete rm in an tes m ediante los m e n o re s
de la p rim e ra co lu m n a
Determinante Determinante Determinante
menor menor menor
d e a d e a 2 d e a 3
i i 1
a, b { cj
a 2 b 2 c 2
a 3 b 3 c 3
= a
b 2 c 2
b 3 c3
- a 2
b C i
b $ c3
+ a 3
b i c,
b2 c2
4 - 2 6
Evalúe 3 5 0
1 -3 -1
resde laprimeracolumna.
utilizandoel desarrollo del determinantemediantelosmeno-
Seguiremoselprocedimiento indicadoenelcuadro.
4 - 2 6
3 5 0
1 -3 -1
= 4 [5 (-l) - (-3)0] - 3[(—2)( —1) - (-3)6] + l[(-2 )0 - 5(6)]
= 4(—5 + 0) - 3(2 + 18) + 1(0 - 30)
= 4(—5) - 3(20) + 1(—30)
= -20 - 60 - 30
= -1 1 0
= 4
5 0
3 -1
- 3
2 6
3 -1
+ 1
- 2 6
5 0
AHORA RESUELVA EL EJERCICIO 13 E l d e te rm in a n te tie n e u n v a lo r d e - 1 1 0 . #](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-310-320.jpg)



![2 8 6 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
37. a - b + 2c = 3
a - b + c = 1
la + ¿> + 2c = 2
38. 2* + y - 2 = 0
3x + 2 y + z = 3
x - 3y - 5z = 5
39. a + Ib + c = 1
a - b + c = 1
2a + ¿> + 2c = 2
40. 4x - 2y + 6z = 2
-6 * + 3y - 9z = - 3
2x - l y + l l z = -5
4L 1.1* + 2.3y - 4.0z = -9.2
-2.3* + 4.6z = 6.9
-8.2y - 7.5z = -6.8
42. 4.6y - 2.1z = 24.3
-5.6* + 1.8y = -5.8
2.8* - 4.7y - 3.1z = 7.0
43. -6 * + 3y - 9z = - 8
5* + 2y - 3z = 1
2* - y + 3z = -5
46. i * - + 3z = -3
2* —3y + 2z = -1
1 1 1 i
6^ + F ' 3Z = 1
44. x —2y + z = 2
4* - 6y + 2z = 1
2* - 3y + z = 0
47. 0.2* - O.ly - 0.3z = -0.1
0.2* - O.ly + O.lz = -0.9
0.1* + 0.2y - 0.4z = 1.7
45. 2* + - y - 3z = 5
-3 * + 2y + 2z = 1
4x ~ y ~ i z = 4
48. 0.6« - 0.4u +0.5w = 3.1
0.5w + 0.2ü +0.2w = 1.3
0.1a + O.lv +0.1w = 0.2
Resolución de problemas
49. Dado un determinante de la forma , ¿cómo carn
a l b i
Ü
2 th
biará el valor del determinante si se intercambian entre sí
a2 b2
las a y se intercambian entre sí las b,
su respuesta.
a, bx
? Explique
50. Dado un determinante de la forma , ¿cómo cam-
a, by
Ü
2 b
>
2
biará el valor del determinante si las a son intercambia-
by O
y
das con las b.
b2 02
? Explique su respuesta.
5L Si las dos filas de un determinante de 2 X 2 son iguales,
¿cuál es el valor del determinante?
Determine el valor de la letra dada.
- 57.
Reto
4 6
- 2 y
= 32 58.
b - 2 - 4
b + 3 - 6
= 14
52. Si todos loselementos de una fila o de una columna de un
determinante de 2 X 2son 0, ¿cuáles el valor del determi
nante?
53. Si todos loselementos de una fila o de una columna de un
determinante 3 X 3 son 0, ¿cuál es el valor del determi
nante?
54 Dado un determinante de 3 X 3,si todos los elementos de
una fila se multiplican por - 1, ¿cambiará el valor del de
terminante? Explique.
55. Dado un determinante de 3 X 3, si la primera y segunda fi
lasse intercambian, ¿cambiará el valordel determinante?
Explique.
56. En un determinante de 3 X 3,si cualesquiera dos filas son
iguales, ¿puede hacer una generalización acerca del valor
del determinante?
59.
4 7 y
3 - 1 2
4 1 5
= -3 5 60.
3 * -2
0 5 - 6
1 4 -7
= -3 1
61. Utilice el método de la suma para resolver el siguiente sistema para a) *, y b) y.
axx + byy = c,
a2x + b rf = c2
Ejercicios de repaso acumulativo
12.5] 62. Resuelva la desigualdad 3(x - 2) < j( x - 4) e indique la solución en notaciónde intervalo.
Grafique 3* + 4y = 8, mediante el método indicado.
[3.2] 63. ft>r medio del trazo de puntos.
64. Utilizando las intersecciones de los ejes x y y.
[3.3] 65. Utilizando la pendiente y la intersección del eje y.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-314-320.jpg)





![2 9 2 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
Sin graficar, determine el número de soluciones para cada uno délos siguientes sistemas de desigualdades. Explique sus respuestas.
47. 2x + y < 6 48. 3x - y < 4
2x + y > 6 3* - y > 4
49. 5^ - 2y < 3
£ 5jc - 2y > 3
50. 2x - y < 7 V 5L 5* - 3y > 5
3x - y < 4 5* - 3y > 6
5Z x + y < 0
* - y > 0
Reto
Determine la soluciónpara cada sistema de desigualdades.
53. y ^ x 2 54. y < 4 - x? 55. y < |x
y < 4 y > - 5 y < 4
56. y > |x - 2|
y < - |x - 2|
Ejercicios de repaso acumulativo
/2 .2 J 57. En física, una fórmula para palancas es fd i + f1dl = Despeje fi de esta fórmula.
[3.2] Establezca el dominio y rango de cada función.
58. {(4,3), (5 ,-2 ), (-1 ,2 ), (0 ,-5 )} 60. y
k
59. f { x ) = x - 4 2'
j
. . / ,
--1
--1
--
-2-
. y i **
(2.-1)
R e s u m e n d e l C A P IT U L O
Términos y frases importantes
4.1 Sistemadeecuaciones 4.4 4.6
Métodode lasuma(o lineales Matriz aumentada Restricciones
eliminación) Elementos Programaciónlineal
Sistemadeecuaciones 4.2 Matriz Sistemadedesigualdades
consistente Interpretacióngeométrica Transformacióndefilas lineales
Sistemadeecuaciones de unsistemade Matrizcuadrada Sistemadedesigualdades
dependiente ecuacioneslineales Formatriangular linealesconvalor
Sistemadeecuaciones contresvariables absoluto
inconsistente 4.5
Témaordenada 4.3 Reglade Cramer
Soluciónde unsistema Anguloscomplementarios Determinante
deecuaciones Ángulossuplementarios Desarrollodel determi
Sustitución nantepor menores
Determinantemenor
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-320-320.jpg)

![Ejercicios de repaso del capítulo
2 9 4 • C apítulo 4 • Sistem as d e e c u a c io n e s y d e sigualdades
[4.1] Escriba cada ecuación en la forma pendiente intersección. Sin graficar ni resolver, determine si el sistema de ecuaciones linea
les es consistente, inconsistente o dependiente. También indique si el sistema tiene exactamente una solución, ninguna solución o un
número infinito de soluciones.
1. 2* - 3y = - 1 2. 2* - 5y = 8 3. y = x + 4 4. 6
x = 4y - &
- 4 x + 6
y = 1 3* + 4y = 9 x + 2y = 8 4* = 6y + 8
Determine gráficamente la solución de cada sistema de ecuaciones. Si el sistema es inconsistente o dependiente, indíquelo.
5. y = x + 3 6
. x = - 2 7. 2* + 2y = 8 8
. 2y = 2x - 6
y = 2x + 5 y = 3 2x - y = - 4 1 _ 1 = 3
2 X 2 y 2
Determínela solución de cada sistema de ecuaciones mediante sustitución.
9. y = —4x + 2 10. 4x —3y = - 1 11. a = 2b - 8 12. 3* + y = 17
y = 3 x - 12 y = - 3x - 4 21, - 5a = 0 1 3
2X ~ 4y = 1
Determine la solución de cada sistema de ecuaciones utilizando el método de la suma.
13. * - 2y = 5 14 - 2 x - y = 5 15. 2a + 3b = 1
2* + 2y = 4 2* + 2y = 6 a - 2b = - 7
16. 0.4* - 0.3y = 1.8 17. 4r - 3s = 8 18. - 2 m + 3n = 15
-0.7* + 0.5y = -3.1 2r + 5s = 8 3m + 3* = 10
2 9 3 5
19. * + - y = - 20. 2* + 2y = 8 2L y = - - * + -
3 . y = 4x - 3 5 7
X ~ 2 y = X + 4 y = 2
22. 2* - 5y = 12 23. 2x + y = 4 24 2* = 4y + 5
4 1 2y = * —6
x - - y = -2 x + - y = 2
[4.2] Determine la solución de cada sistema de ecuaciones utilizando el método de sustitución o el de la suma.
2 5 . * —2y —4z = 13 2 6 . 2 a + ¿ > - 2 c = 5 27. * + 2y + 3z = 3
3y + 2z = - 2 3b + 4c = 1 -2 * - 3y - z = 5
5z = -2 0 3c = - 6 4* + 2y + 5z = -8
28. - * —4y + 2z = 1 29. 3y - 2z = - 4 30. 3a + 2b - 5c = 19
2* + 2y + z = 0 3* - 5z = - 7 2a - 3b + 3c = -1 5
-3 * - 2y - 5z= 5 2* + y = 6 5 a - 4 b - 2 c = - 2
31. * - y + 3z = 1
- * + 2y - 2z = 1
* - 3y + z = 2
32. -2 * + 2y - 3z = 6
4* - y + 2z = -2
2* + y - z = 4](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-322-320.jpg)
![Ejercicios d e re p a so del capítulo • 2 9 5
[4 .3 ] Exprese cada problem a com o un sistema de ecuaciones lineales y utilice el m étodo de su elección para determinar la solución.
33.
34.
35.
EdadesJorge Valdés es 10 años mayorque su sobrina Jen- 36.
nifer. Si la suma de sus edades es 66,determine la edad de
Jorge y la edad de Jennifer.
Velocidad del viento Un avión puede viajar a 560 millas
por hora con el viento a favor y a 480 millas por hora con 37.
el viento en contra. Determine la velocidad del viento y
la velocidad del avión sin viento.
Mezcla de soluciones Jaime Cervantes tiene dos solucio
nes áridas con las características que se muestran en la si
guiente figura. ¿Qué cantidad de cada una debe mezclar
para obtener6 litros de una solución de ácido con concen
tración de 40%? 38.
..
7 0 -
60
50
40 -
30
2 0 -
10
20%
50%
o
Solución Solución
A B
[4.4] Resuelva cada sistema de ecuaciones utilizando matrices.
Fútbol La admisión a un partido de fútbol cuesta $15 por
adulto y $11 por niño.Si se vendió un total de 650 boletos
por un monto de $8790, determine cuántos boletos para
niños y cuántos boletos para adultos se vendieron.
Regresó al espacio John Glenn fue el primer astronauta
estadounidense en dar la vuelta a la Tierra. Muchos años
después de esta hazaña, Glenn regresó al espacio. Esta vez
tenía cinco años menos que el doble de su edad cuando
hizo el primer viaje. La suma de la edad que tenía en
cada ocasión es 118. Determine qué edad tenía en cada
uno de sus viajes.
Cuenta de ahorros MarciaTorres tiene un total de $40,000
invertidos en tres cuentas de ahorro diferentes. Parte del
dinero está invertido en una cuenta que otorga 7% de in
terés; en la segunda cuenta tiene $5,000 menos que en la
primera, y recibe 5% de interés; la tercera cuenta le da 3%
de interés Si el monto total que recibe Marcia al año por
concepto de interés es de $2300,determine cuánto dinero
tiene invertido en cada cuenta.
39. x + 5 y = 1
- 2 x - Sy = - 6
40. 2x - 3y = 3
2x + 4y = 10
4L y = 2x - 4
4x = 2y + 8
4Z 2 x - y - z = 5
x + 2y + 3z = -2
3x - 2y + z = 2
43. 3a - b + c = 2
2a - 3b + 4c = 4
a + 2b - 3c = - 6
44 x + y + z = 3
3x + 2y = l
y - 3 z = -1 0
[4.5] Resuelva cada sistema de ecuaciones utilizando determinantes.
45. l x - Sy = -1 0
-5 * + 4y = 2
46. x + 4y = 5
- 2 x - 2y = 2
47. 4m + 3n = 2
Im - 2n = -1 1
48. p + q + r = 5
2p + q ~ r = - 5
- p + 2q - 3r = - 4
49. -2 a + 3b - 4c = -7
a + b + c = 4
-2 a - 3b + 4c = 3
50. y + 3z = 4
- x - y + 2z = 0
x + 2y + z = l
[4.6] Determine gráficamente la solución de cada sistema de desigualdades.
51. - x + 3y > 6
2x - y < 2
52. 5* - 2y < 10
3x + 2y > 6
53. y > 2x + 3
y < - x + 4
54 x > ~2y + 4
1 3
y < ~ 2x~2
Determine la solución de cada sistema de desigualdades.
55. x > 0
y > 0
x + y < 6
4x + y < 8
56. x > 0
y > 0
2x + y < 6
4 r + 5y < 20
57. x < 3
Ivl > 2
58. |*| > 4
|y - 2| £ 3](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-323-320.jpg)

![E x a m e n de re p a so acum ulativo • 2 9 7
22. Mezcla de soluciones Teresa Muñoz, una química, tiene
soluciones con concentración de 6% y 15% de ácido sul
fúrico. ¿Qué cantidad de cada solución debe mezclar pa
ra obtener 10 litros de una solución con concentración de
9%?
23. Suma de números La suma de tres números da por resul
tado 25. El número más grande es tres veces el número
más pequeño, y el tercer número es uno más que el doble
del número más pequeño. Determine los tres números.
Determine la soluciónpara cada sistema de desigualdades.
24 3* + 2y < 9
- 2 x + 5y < 10
25. x
Examen de repaso acumulativo
Resuelva el examen y verifique sus respuestas con lasque aparecen alfinal. Revise laspreguntas que haya respondido incorrectamen
te . Los números de la sección y el objetivo en donde seanaliza el material correspondiente seindican después de cada respuesta.
L Evalúe 16 -s- “ 32 j-
2. Considere el siguiente conjunto de números.
-4 ,9 ,0 , V5, -4.63,1}
Indique los elementos del conjunto que sean
a) números naturales;
b) números racionales;
c) números reales.
3. Escriba los siguientes números de menor a mayor.
-1. M .f .f .- |- 8 |,|- i o |
Resuelva.
4. - [ 3 - 2 (x - 4)] = 3 (x - 6)
6. 2 x - 3| - 4 = 5
7. Despeje x de la fórmula A
1 - ^ (a + x) por x
8. Determine el conjunto solución de la desigualdad.
o < ^ 2 , 8
9. Simplifique
3 * y
10. Grafique 2y = 3x - 8
11. Escriba en forma pendiente intersección la ecuación de la
recta paralela a la recta 2x - 3y = 8 y que pasa porel pun
to (2,3).
12. Grafique la desigualdad 6
x - 3y < 12.
13. Determine cuáles de las gráficas siguientes representan
funciones. Explique.
b) y
2*4-
C)
- 2 - - 2 x
- 2 2 *
- 2 -
14. si / W = 4 ^ f . determine a) / ( —
4) b) f ( h) y
O /(3)
Resuelva cada sistema de ecuaciones.
15. 3x + y = 6
y = 2x + 1
16. 2p + 3q = 11
- 3 p - 5q = -1 6
17. x - 2 y = 0
2x + z = 7
y - 2 z = - 5
18. Ángulos de un triángulo Si el ángulo mayor de un trián
gulo mide nueve veces lo que el ángulo menor, y el ángu
lo mediano mide 70° más que el más pequeño, determine
la medida de tos tres ángulos.
19. Caminar y trotar Dolores Castro camina a una velocidad
efe4 millaspor hora, y Judit Páez trota a 6 millaspor hora.
Dolores comienza a caminar { hora antes de que Judit
comienza a trotar. Si Judit trota siguiendo la misma ruta
que Dolores, ¿en cuánto tiempo Judit alcanzará a Dolores?
20. Concierto de rock Las entradas a un concierto de rock tie
nen dos precios diferentes. Las más caras se venden a $20
y las más baratas a $16.Si se vende un total de 1000 boletos
por un monto de $18,400, ¿cuántas entradas de cada tipo
se vendieron?](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-325-320.jpg)
![Respuestas al examen de repaso acumulativo
2 9 8 • C apítulo 4 • Sistem as d e e c u a c io n e s y de sigualdades
L l ; [Sec 1.4,Obj.3] l a ) 9,1 b) | , -4 ,9 ,0 , -4.63,1 c) -4 ,9 ,0 , V 3, -4.63,1; [Sec. 1.2,Obj. 5]
3 .- | - 8 | , - l , f . f , |-4 |, |-1 0 |; [Sec. 1.3,O bj.l] 4 7; [Sec. 2,1, Obj. 3] 5 .^ -; [Sec. 2.1,Obj. 4] 6 .6 ,-3 ; [Sec.2.6,Obj. 2]
1.x = 2 M - a; [Sec 2.2,Obj. 2] 8. j * | | < * < y }; [Sec.2.5,Obj.3] 9 . ^ ; [Sec. 1.5,Obj. 7]
; [Sec.3.3, Obj. 2] 11. y = + | ; [Sec 3.5, Obj. 3] 12. y
4
2+
/
m u — i /
- 4 - 2 -- / 2 4
- 2 - /
[Sec. 3.7, Obj. 1] 13.a) función b) función c) no es función; [Sec.3.2, Obj. 3] 1 4 a) ~ b) ^ + ^
c) indefinido; [Sec. 3.2, Obj. 4] 15.(1, 3); [Sec. 4.1, Obj. 2] 16. (7 ,-1 ); [Sec. 4.1, Ob. 3] 17. (2,1, 3); [Sec. 4.2, Obj. 1]
18.10°, 80°, 90°; [Sec. 2.3, Obj. 2) 19.1 hora; [Sec. 2.4, Obj. 1] 20.600 a $20,400 a $16; [Sec. 43, Obj. 1]](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-326-320.jpg)



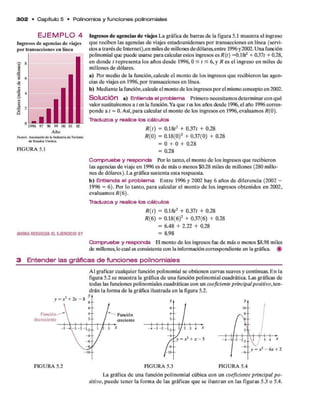



![Sección 5.1 • S u m a y resta d e polinom ios • 3 0 7
Indique a) d grado de cada polinomio y b) su coeficiente principal.
2 9 . a 4 + 3 a 6 - 2 a - 1 0
- 3L 4 * y + 6xy* + 9 x /
33. -J m V p ® + | m 3p6 -
Evalúe cada función polinomial en el valor dado.
35. Determine P(2),si P(x) = x2- 6 a + 1.
« 37. Determine ^ Q ^ - s i p (/ = 2
x2- 3 x - 6
.
39. Determine P(0.4),si P(x) = 0 .2 a 3 + 1.6*2 - 2.3.
Simplifique.
4L ( a 2 + 3 * - 7 ) + ( 6 * - 5 )
43. (x 2- 8 a + 2) - (5x + 9)
45. ( 4 / + 9y - 1) - ( 2 / + 1 0 )
47. ( - J , +« ) + ( “ I " 2 - - X)
49. (1 .4 a:2 + 1 .6 a - 8 .3 ) - (4 .9 a 2 + 3 .7 a + 1 1 .3 )
5L ( - J*3+x*y + 8*y2
) + (-*3- |A + x f)
£ 53. (3a - 6
b + 5c) - ( - 2 a + 4b - 8
c)
55. (3a2b - 6ab + 5b2) - (4ab - 6b2- 5a2
b)
57. (8r2- St2+ 2rt) + (-6 /7 + I t2- r2)
59. 6 a 2 - 2 a - [3 a - (4 a 2 - 9 ) ]
61. 5to - (no2~ [(3to - 2w 2) - (4w + w 2)]
63. Reste (4 a - 1 1 ) de (7 a + 3).
« 65. Sume - 2 a 2 + 4a - 12 y - a2 - 2a .
67. Reste 0.2a2 - 3.9a + 26.4 de -4.2a2 - 9.6a.
69. Reste ^ A 2y + de ( - x 2y + A y2 + |
30. - 2 a 4 + 6 a 5 - a 7 + 5 a 3
32. - a W + 7 a W - 5 fl?c2#
34. - 0 . 6 a 2/ / - 2 . 9 a > / - 1 .3 a 8/
36. Determine P( - 1) ,si P ( a ) = 4 a 2 + 6a + 12.
38. Determine si P (a ) = ^ a3 - a 2 + 6.
40. Determine P (-1.2),si P (a) = -1.6*3 - 4 .6 a 2 - 0 .1 a .
42 ( 5 b 2 - 4 b + 7) - (2¿>2 - 3 b - 5 )
44. ( 2 a - 5) - ( 3 a 2 - 4 a + 1 6 )
46. (5 /í2 - 7) + (2 /i2 + 3 n + 1 2 )
48. ( 6 / - 9 y + 4 ) - ( - 2 / - y - 8 )
50. ( - 12.4A 2y - 6.2a> - + 9 . 3 / ) - ( - 5 .3 A 2y + 1.6xy - 1 0 . 4 / )
a ( - k + l ) - ( - l " , + ! )
54 ( 6 r + 7s - t ) + ( - 2 r - 2s - 5 t )
56. ( 3 a 2 - 5 / - 2 a / - ( 4 a 2 + 8 / - 9 a /
58. (a2 - ¿>
2 + 5a¿) + ( - 3 b 2- lab + a2)
60. 3 a / - 2 a - [ - ( 4 a / + 3 a ) - 5 a /
62 - [ —(5r2 - 3r) - (2r - 3r2) - 2 / ]
64 Reste ( —a 2 + 3 a + 5 ) de (4 a 2 — 6 a + 2 ).
66. Reste (5 a 2 - 6 ) de (2 a 2 - 4 a + 8).
68 . Sume 6 a 2 + 3Ay y - 2 a 2 + 4Ay + 3y.
70. Reste (6x2y + 3 a / de (2 /y + 1 2 a / .
Simplifique. Suponga que todos los exponentes representan números naturales.
7L ( 3 a * - 7 a ' + 1) + ( 2 a 2' - 3a ' + 2 ) 72 (bx2
' - 5 a ' + 4) + ( 2 a 2' + a ' + 3 )
73. (a25 - 8a s + 6) - (2 a 2* - 4 a 5 - 9) 74. (5a2" - 6a" + 4) - (2a2" + 7)
75. (7b*" - 5b2
" + 1) - (3b3" - b2
") 76. (-3 r 3*+ r* - 6) - ( - 2 r3*- 5 r* + 6)
Resolución de problemas
En los ejercicios 77 a 82, determine una expresión para el perímetro de cadafigura. Véase el ejemplo 9.
78.
Cuadrado Rectángulo
í 2 + 2 t + 5 x ? - x + 7](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-335-320.jpg)
![3 0 8 • C apítulo 5 • Polinom ios y fun cione s polinom iales
79.
81.
*2 + 8
x2+ 3x + 1
80.
8Z
x2 + 3
7x + 9
8x + 7
83. ¿La suma de dos trinomios siempre da por resultado un
trinomio? Explique y proporcione un ejemplo que susten
te su respuesta.
84. ¿La suma de dos binomios siempre da por resultado un
binomio? Explique y proporcione un ejemplo que susten
te su respuesta.
85. ¿La suma de dos polinomios cuadráticos siempre da por
resultado un polinomio cuadrático? Explique y propor
cione un ejemplo que sustente su respuesta.
86. ¿La diferencia de dos polinomios cúbicos siempre da por
resultado un polinomio cúbico? Explique y proporcione
un ejemplo que sustente su respuesta.
87. Área El área de un círculo es una función de su radio, en
donde A(r) = i t i2. Determine el área de un círculo si su
radio mide 6 pulgadas. Utilice la tecla [tt] de su calcula
dora.
88. Globo El volumen de una esfera es una función de su ra
dio, en donde V (r) = j i r r Determine el volumen de un
globo esférico cuando su radio mide 4 pulgadas.
^ 89. Altura Cuando un objeto se deja caer desde el edificio
Empire State (altura = 1250 pies), la altura del objeto, h,
en pies, respecto del piso en el instante t, en segundos, des
pués de que se ha soltado, puede determinarse mediante
h = P{t) = -1 6 í2 + 1250
Determine a qué distancia del piso se encuentra un obje
to 6 segundos después de que se ha dejado caer.
90. Concurso de ortografía El número de maneras en que
puede seleccionarse a los ganadores del primero, segun
do y tercer lugares en un concurso de ortografía entre n
participantes, está dado por P(n) = n3- 3n2+ 2n. Si hay
seis participantes, ¿de cuántas maneras pueden seleccio
narse el primero, segundo y tercero lugares?
Utilidad La utilidad de una compañía se determina restando sus costos de sus ingresos. En los ejercicios 91 y 92, R(x) representa el
ingreso de la compañía cuando se venden x artículos, y C(x) representa el costo de la compañía cuando seproducen x artículos, a)
Determine una función déla utilidad P(x). b) Evalúe P(x), cuando x = 10
0
.
x2+
9L R(x ) = 2x2- 60x,
C( x) = 8050 - 420x
92. R(x) = 5.5x2 - 80.3*
C( x ) = 1.2*2 + 16.3* + 12,040.6](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-336-320.jpg)


![S e cció n 5.2 • M ultiplicación d e polinom ios • 311
104. y = 2x4 + 9x¿ - 5
c)
Actividad en equipo
Analicen y respondan en equipo los ejercicios 105 y 106.
105. Siel término principal de una función polinomial es 3X3, ¿cuál de las siguientes podría ser la gráfica del polinomio? Expliquen.
Consideren lo que sucede cuando x tiene valores positivos grandes, y cuando x tiene valores negativos grandes.
c)
106. Si el término principal de un polinomio es - 2x4, ¿cuál de las siguientes podría ser la gráfica del polinomio? Explique.
a)
l)
b)
Ejercicios de repaso acumulativo
[1.4] 107. Evalúe-^81.
1 4 1
[2.1] 108. Resuelva - =
[2.4] 109. Máquinasdemodelado Una vieja máquina de mo
delado puede producir 40 cubetas de plástico en
una hora. Una máquina más nueva puede fabricar
50 cubetas en una hora. ¿Cuánto tiempo les tomará
a las dos máquinas producir un total de 540 cubetas?
[3.4] 110. Determine la pendiente de la recta que pasa por los
puntos (8, —
4) y ( —
1, - 2).
[4.2] 111. Resuelva el sistema de ecuaciones.
—4s + 3/ = 16
2t - 2u = 2
—s + 6
u = -2
5 . 2 M U L T IP L IC A C IÓ N D E P O L IN O M IO S
1 M u lt ip lic a r u n m o n o m i o p o r u n p o lin o m io .
2 M u lt ip lic a r u n b i n o m i o p o r u n b in o m io .
3 M u lt ip lic a r u n p o lin o m io p o r u n p o lin o m io .
4. D e t e r m i n a r e l c u a d r a d o d e u n b in o m io .
5 D e t e r m i n a r e l p r o d u c t o d e la s u m a y d i f e r e n c ia d e lo s m is m o s
d o s t é r m i n o s ( p r o d u c t o d e b i n o m io s c o n j u g a d o s ) .
6 D e t e r m i n a r e l p r o d u c t o d e f u n c i o n e s p o lin o m ia le s .](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-339-320.jpg)



![S e cció n 5.2 • M ultiplicación d e polinom ios * 3 1 5
4 Determinar el cuadrado de un binomio
Ahoraestudiaremosalgunasfórmulasespeciales. Confrecuencianecesitamoscalcular
elcuadrado de un binomio, asíque contamosconfórmulasespecialesparahacerlo.
C u a d ra d o d e un binom io
(a + f>
)2= a2+ lab + b2
(a - b)2 = a2 - lab + b2
Siustedolvidalasfórmulas,puedededucirlasfácilmentemultiplicando (a + b)(a - b) y
( a - b ) ( a - b ) .
Los ejemplos7y8ilustranelusodelafórmulaparaelcuadradodeun binomio.
E J E M P L O 7 Desarrolle, a) (3* + 5)2 b) (4X2 - 3y f
S o lu c ió n a) (3* + 5)2 = (3a:)2 + 2(3*)(5) + (5)2
= 9x2 + 30* + 25
b) (4** - 3y)2= (ó*2)2 - 2(4*2)(3y) + (3y)2
= 16*4 - 24*2
y + 9y2 #
El cuadrado de los binomios, comoen el ejemplo 7, también sepuede calcular
medianteel método PIES.
C Ó M O E V IT A R Siem
prerecuerdeeltérminodeenm
edioalcalcularelcuadradodeunbinom
io.
E R R O R E S C O M U N E S
C o r r e c t o In c o r r e c t o
(x + 2 ) 2 = (x + l) (x + 2 )
= x2+ 4x + 4
( * - 3 ) 2= ( * - 3 ) ( * - 3 ) p ^ - S ) ? - j £ = l|=9
= x 2 - 6 * + 9
E J E M P L O 8 D esarrolle [x + (y - 1)]2.
Solución E ste problem a parece más com plicado q u e los ejem plos anteriores, pero se resuelve
d e la misma form a q u e los otros cuadrados d e binomios. C onsidere a x com o el prim er
térm ino y a (y - 1 ) com o el segundo. Utilice dos veces la fórmula.
[* + (y - l)]2 = ( * ) 2 + 2(*)(y - 1) + (y - l)2
= x 2+ {2x ) ( y - 1) + y 2- 2y + 1
= x 2+ 2x y - 2x + y 2- 2y + 1
N inguno d e los seis térm inos son térm inos sem ejantes, p o r lo q u e no se pueden re
ducir. O bserve q u e (y - 1)2 tam bién es el cuadrado d e un binomio, y fue desarrollado
AHORARESUELVAELEJERCICIO 51 com o tal. #
5 Determinar el producto de la suma y diferencia de los mismos dos términos
(binomios conjugados)
A continuación m ultiplicarem os (x + 6)(x - 6) utilizando el m étodo PIES.
( x + 6 )(* - 6) = x 2- 6
x + 6
x - (6)(6) = x 2- (?
O bserve q u e los productos externos e internos sum an cero. A l exam inar este ejem plo,
vemos q u e el producto d e la sum a y la diferencia d e los mismos dos térm inos es la di
ferencia d e los cuadrados d e los dos términos.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-343-320.jpg)
![3 1 6 • C a p ítu lo s • Polinom ios y fun cione s polinom iales
P rod ucto d e la su m a y diferencia d e los m ism o s d o s
térm inos (b in o m io s co n ju g a d o s )
E J E M P L O 9
(a + b ) ( a - b ) = a 2 - b 1
E n otras palabras, p ara m ultiplicar dos binom ios q u e sólo difieren en el signo
en tre sus dos térm inos, reste el cuadrado del segundo térm ino del cuadrado del prim e
ro. O bserve q u e a2- b2 representa una diferencia de dos cuadrados.
M ultiplique, a) - | j b) (0.2* + 0.3z2)(0.2* - 0.3Z2)
S o l u c i ó n C ada uno es un producto d e la sum a y diferencia d e los mismos dos térm in o s, es d e
cir, son binom ios conjugados. Por lo tanto,
. , ( „ +i ) ( 3 , ( ! ) ’ = » , - ±
b) (0.2* + 0.3Z2) (0.2* - 0.3z 2) = (0.2*)2- (0.3z2)2
= 0.04*2 - 0.09z4 #
E J E M P L O 1 0 M ultiplique (5* + y 3) (5* - y3).
Solución (5* + / ) ( 5 * - y3) = (5*)2 - (y5)2 = 2S*2 - y6 #
E J E M P L O 11 M ultiplique [4* + (3y + 2)][4* - (3y + 2)].
S o l u c i ó n TVatamos a 4* com o el prim er térm ino y a 3y + 2 com o el segundo. E n consecuencia,
obtenem os la sum a y la diferencia d e los mismos dos términos.
[4* + (3y + 2)][4* - (3y + 2)] = (4*)2 - (3y + 2)2
= 16*2 - (9y2 + 12y + 4)
AHORARESUELVAELEJERCICIO 55 = 16*2 - 9y2 - 12y - 4 #
E J E M P L O 1 2 Área La figura 5.11 consiste d e un cuadrado y dos rectángulos. D eterm ine una expre
sión polinom ial p ara calcular el área total d e la figura.
S o IU C ¡Ó n Para determ inar el área total, encuentre las áreas d e las tres regiones y
luego súmelas.
Á rea del cuadrado = * • * = x2
Á rea del rectángulo d e la derecha = * - 4 = 4*
Á rea del rectángulo inferior = * * 5 = 5*
FIGURA 5.11 ,
E l área total es la sum a d e estas tres cantidades.
AHORARESUELVAELEJERCICIO 85 Á rea total = X? + 4* + 5* = X2+ 9*. #
6 D e te rm in a r el p ro d u c to d e fu n c io n e s p o lin o m ia le s
A ntes se m encionó q u e p ara funciones /(* ) y g(*), ( /• g)(*) = /(* ) • g(*). A hora re
solverem os un ejem plo q u e incluye multiplicación d e funciones polinomiales.
E J E M P L O 1 3 Sea /(* ) = * + 4 y g(*) = * - 2. D eterm ine
a > /( 3 ) ’*(3) b) (/-g )(* ) c) (/'g ) ( 3 )
Solución a) /(* ) y g(*) son funciones polinom iales, ya q u e las expresiones a la derecha d e los
signos d e igual son polinomios.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-344-320.jpg)

![3 1 8 • C a p ítu lo s • Polinom ios y fun cione s polinom iales
5 . a ) ¿Qué se entiende por el producto de la suma y la dife
rencia de los mismos dos términos (producto de bino
mios conjugados)?
b) Proporcione ejemplo de un problema que sea produc
to de la suma y diferencia de los mismos dos términos
(binomios conjugados).
c) ¿Cómo se multiplicaelproducto de la suma y la diferen-
da de los mismos dos términos (binomios conjugados)?
d) Multiplique el ejemplo que dio en la parte b) median
te el procedimiento de la parte c).
Problemas de aplicación______________
Multiplique.
9. {4 x y ){6 x /)
- "■ 6 'V ) ( I 'W )
1 3 . - 3 x 2
y ( - 2 x 4
y 2+ 3xy 3+ 4 )
15. | y z ( 3 * + 4 y - 9 y 2)
17. 0 .3 (2 a 2 - 5 a + 7 y )
19. 0.3a5
b4
(9.5a6b - 4 .6 a4
b3+ 1 .2 ab5)
Multiplique los siguientes binomios.
2 1 . (4 a - 6 ) (3 a - 5 )
£ 23. ( 4 - a ) ( 3 + 2 a 2)
2 5 . [ x + 2 y ) ( l x - | r )
2 7 . (0.3a + 5b)(2a - 0 .7 b)
Multiplique los siguientes polinomios.
29. (a 2 + 3a + 1 ) ( a - 2 )
3 1 . (a - 3b)(2a2- ab + 2b2)
3 3 . (a 3 - a 2 + 3 a + 7 ) (a + 1 )
3 5 . (5 a 3 + 4 a 2 - 6 a + 2 ) ( a + 5 )
3 7 . (3 m 2- 2m + 4 )(m 2- 3m - 5 )
3 9 . ( 2 a - l ) 3
4 1 . ( 5 r 2 — rs + 2s2)(2r2 — s2)
Multiplique mediante lafórmulapara el cuadrado de un binomio
mismos dos términos (producto de binomios conjugados).
& 4 3 . ( a + 2 ) ( a + 2 )
4 5 . (2 a - 3 ) ( 2 a - 3 )
4 7 . (4 a - 3 y ) 2
£ 4 9 . ( 5 m 2 + 2n)(5m2- 2n)
5 1 . [ y + ( 4 - 2 a ) ] 2
5 3 . [5 a + ( 2 y + 3 ) ] 2
5 5 . [a + (b + 2 )][a - (b + 2 ) ]
6. ¿El producto de dos binomios siempre da por resultado un
a) binomio?
b) ¿Trinomio? Explique.
7. ¿El producto de dos polinomios de primer grado siempre
será un polinomio de segundo grado?
8. a) Dadas f(x) y g(A), explique cómo determinaría
(f ' g) ( *)•
b) Sif(x) = x - 2 y g(x) = x + 2,determine (f •g) (a).
10. ( - 2 A y 4)(3 A 4y 6)
12. 2y3(3y2 + 2y - 6)
14. 3A4(2 A y 2 + 5 a 7 - 6y)
16. ~ x 2
y(4x5
y 2+ 3a - 6y2)
18. 0.8(0.2a + 0.9b - 1.3c)
20. - 2.bm3
r? + 5.9n4)
22. ( 2 a - 1 ) (5 a + 7 )
24. (5 a + y)(6A - y)
*• 6 a + - b)
28. (4.6r - 5.8s)(0.2r - 2.3s)
30. (a + 3 )(2 a 2 - a - 9)
32. ( I p - 3 )(-2 p 2 - 4 p + 1)
34. ( 2 a - 1 ) ( a 3 + 3 a 2 - 5 a + 6 )
36. (a3- 2a2+ 5a - 6)(2a2- 5a - 2)
38. (2 a 2 - 6
a + 3)(3a2- 5a - 2)
40. (3 a + y)3
42. (4 a 2 - 5Ay + y2)(A2 - 2y2)
bien utilizando la delproducto de la suma y diferencia de los
44. (y - 4)(y - 4)
46. (3z + 5)(3z + 5)
48. (2a + 5b)2
50. (5p2 + 6c/2)(5p2 + ó^2)
52. [(a + b) + 9]2
54. [ 4 — ( p — 3^)]2
56. [2 a + (y + 5 ) ] [ 2 a - (y + 5)]](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-346-320.jpg)
![S e cció n 5.2 • M ultiplicación d e polinom ios • 3 1 9
Multiplique.
59. x y 4 x 2 + 3*y - l y 2)
6L - y x y V ^ - x y V - 5x y +
63. (3a + 4 )(7a - 6)
65. ( a * + i ) ( s x -
67. (2* - 9y)2
f i 69. (x + 3 )(2*2 + 4* - 3)
7L (2 p - 3q)(3p2+ 4W - 2*2)
73. [(3x + 2) + y)[(3* + 2 ) - y]
75. (a + b)(a - b)(a2 - ¿>
2)
77. (x - 4 )(6 + x )(2 x - 8)
Rtra las funciones dadas, determine a) (/• g)(x) y b) (f- g)(4).
79. f ( x ) = x - 5 , g ( x ) = x + 4
£ 8L f ( x ) = l x 2+ 6
x - 4, g(x) = 5x + 3
83. /( x ) = - x 2+ 3x, g(x) = x 2+ 2
57. 2 x y ( x 2 + x y + 3 y 2) 58.
60. + ^ x y + 3)
62- f * 2/ ( f * > 3 - x ' y + 2x y h s)
64. (5p - 9q)(4p - q )
66. f a - j f a + j )
68. ( 2* + i ) 3
70. (5a + 4)(a2- a + 4)
72. (2m + /i)(3/w2 —m n + 2a2)
74. [ a + (3b + 4)][a - (3Z> + 4)]
76. (2a + 3)(2a - 3)(4a2 + 9)
78. (3x - 5)(5 - 2*)(3* + 8)
80. f ( x ) = 2
x - 3,g(x) = x - 6
82. f ( x ) = 4 x 2+ 7, g(x) = 2 - x
& 84. f ( x ) = - x 2 + 2x + 7, g(x) = x 2 - l
Resolución de problemas
En los ejercicios 85 a 8
8
, determine una expresión polinomialpara calcular el área total de cada figura.
85. 86.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-347-320.jpg)

![S e cció n 5.3 • División d e polinom ios y división sintética • 3 2 1
103. Interés compuesto La fórmula para calcular el interés
compuesto es
/ r '*
A =
- K i + í ) '
donde A es el monto, P es el capital invertido, r es la tasa
de interés anual, n es el número de veces que el interés se
paga cada año y t es el tiempo en años,
a) Simplifique esta fórmula para n = 1.
b ) Determine el valor de ;4 ,s i P = $1000, n = 1, r = 6%
y t = 2años.
104. Interés compuesto Utilice la fórmula indicada en el ejer
cicio 103 para determinar y4,si P = $4000,n = 2,r = 8%
y t = 2años.
105. Si f(x) = x2- 3x + 5,determinef(a + b) sustituyendo ca
da x de la fórmula por (a + b).
106. Si/(x) = 2X2 - x + 3, determine/(a +b).
En los ejercicios 107 a 112, simplifique. Suponga que todas las variables representan números naturales.
107. 3*'(5*2'" 1 + 6**)
109. (6
x m - 5 )(2 x ^ - 3)
m. ( y - T b
108. 5kr+2
(4kr
+
2- 3k ' - k)
110. (**" - y 2
j')(x2jt + 2y 4n)
112. (am+n)m+n
En los ejercicios 113 y 114, realice la multiplicación polinomio!.
m (x - 3,)*
115. a) Explique cómo puede verificarse por medio de una cal
culadora graficadora una multiplicación en una variable,
tal como {x1+ 2
x + 3)(x + 2) = x3 + 4x2+ Ix + 6.
b) Compruebe la multiplicación indicada en la parte a)
con ayuda de su calculadora graficadora.
114. (2a - 4b)4
1
116. a) Con ayuda de su calculadora graficadora, muestre que
b multiplicación (x2- 4x - 5)(* - l j ^ j ^ + ó ^ - S x + ó.
b) Multiplique (x2 - 4x - 5)(x - 1).
c) Compruebe en su calculadora graficadora la respues
ta que dio en la parte b).
Reto
Multiplique.
117. [ ( y + l ) - ( x + 2 )]2 118. [(a - 2) - (a + 1)]=
Ejercicios de repaso acumulativo
4 / 3
1.3] 119. Evalúe y - [ -
.5] 120. Simplifique
4 - 1 )
2r V Y
[2.5] 12L Resuelva la desigualdad -1 2 < 3x - 5 ^ -4 ,e in
dique la solución en notación de intervalo.
[3.2] 122. Sig(x) = -x 2 —2x + 3, determine
5 . 3 D IV IS IÓ N D E P O L IN O M IO S Y D IV IS IÓ N S I N T É T IC A
S
1 Dividir un polinomio entre un monomio.
2 Dividir un polinomio entre un binomio.
3 Dividir polinomios mediante la división sintética.
4 Utilizar el teorem a del residuo.
1 D ividir u n p o lin o m io e n tre u n m o n o m io
E n la división d e polinom ios, la división entre 0 no está perm itida. C uando se nos da
un problem a d e división con una variable en el denom inador, siempre supondremos que
el denom inador es diferente de 0.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-349-320.jpg)










![3 3 2 • C apítulo 5 • Polinom ios y fun cione s polinom iales
109. Ladivisiónsintética puede utilizarse paradividirpolinomios
entre binomios con la forma ax - b, a J=1. Para realizar
esta operación, divida ax - b entre a para obtener x ~ ~-
Luego coloque la izquierda de los coeficientes numéri
cos del polinomio. Resuelva el problema como se explicó
previamente. Después de sumar los valores numéricos de
bajo de la línea, divida todos ellos, excepto el residuo,
entre a. Después escriba el cociente del problema utilizan
do esos números.
a) Utilice este procedimiento para dividir 9X3 + 9x* + 5x
+ 12entre 3x + 5.
b) Explique por qué no dividimos el residuo entre a.
Ejercicios de repaso acumulativo
8.45 X 102
5
[1.6
] 110. Divida ‘ --- —tj y exprese la respuesta en no-
4.225 X 10
tación científica.
[2.3] 111. Triángulo Determine los tres ángulos de un trián
gulo, si uno de ellos mide el doble del ángulo más
pequeño, y el tercero mide 60° más que el ángulo
más pequeño.
[2.6
] 112. Determine el conjunto solución para
5* ~ 3 + 3 = 7.
[3.6] 113. Sea f(x) = x1- 4 y g(x) = - 5 x + 3. Determine
/(6)*(6).
[5.1] 114 Sume (6r + 5s - /) + (—
3 r - 2s - 5l).
5 .4 FACTO RIZACIÓ N D EL FA C TO R C O M Ú N DE LO S TÉR M IN O S
DE UN PO LIN O M IO Y FACTO R IZACIÓ N POR A G R U P A CIÓ N
t
1 Determinar el máximo factor com ún.
2 Factorizar un m onom io de un polinomio (factorizar el factor
com ún).
3 Factorizar un factor binomial com ún.
4. Factorizar por agrupación.
L a facíorización es la operación opuesta a la multiplicación. Factorizar una expresión
significa escribirla com o un producto d e otras expresiones. Por ejem plo, en la sec
ción 5.2 aprendim os a realizar las siguientes multiplicaciones:
3 * 2(6* + 3 y + 5 x 3) = l S x 3+ 9 x2y + 15x5
y
(6x + 3y ) ( 2 x ~ 5y ) = 12x2- 24x y - 1 5 f
E n esta sección, aprenderem os a determ inar los factores efe una expresión dada. Por
ejem plo, aprenderem os cóm o realizar cada una d e las siguientes factorizaciones.
18*3 + 9 * 2.y + 15X5 = 3 x 2{6x + 3y + 5 x3)
y
12a:2 - 24*y - 15y2 = (6
x + 3 y ) ( 2 x - 5y )
1 D e te rm in a r el m á x im o fa c to r c o m ú n
Para factorizar un monomio d e un polinom io, factorizam os al m áxim o factor común
(M FC) d e cada térm ino del polinomio. E l M FC es el producto d e los factores com u
nes a todos los térm inos del polinom io. Por ejemplo, el M FC p ara 6
x + 15 es 3, ya que](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-360-320.jpg)

![3 3 4 • C apítulo 5 • Polinom ios y fun cione s polinom iales
E J E M P L O 4
Solución
AHORARESUELVAELEJERCICIO 19
E J E M P L O 5
Solución
E J E M P L O 6
Solución
AHORARESUELVAELEJERCICIO 65
Factorice20a3
/ + 6a2
/ -12*/.
El MFC es2a/. Escribacadatérminocomoproductodel MFC y otroproducto. Luego
factoriceel MFC.
20a3/ + 6 a2/ - 12a/ = 2a/ • 10a2 + 2a/ ■3a^ - 2 a/ - 6 /
= 2a/(10a2+ 3xy - 6/)
C o m p ro b a c ió n 2a/(10a2 + 3xy - 6 / ) = 20a3
/ + 6a2
/ - 12a/ #
Cuandoelcoeficienteprincipalde unpolinomioesnegativo,por logeneral factoriza-
mos un factor común con un coeficiente negativo. Esto da como resultado que el
polinomio restantetengauncoeficienteprincipal positivo.
Factorice a) -12a - 18 b) -2b3 + 6b2- 18b
Como loscoeficientesprincipalesenlaspartesa) y b) sonnegativos,factorizamosfac
torescomunesconuncoeficientenegativo.
a) —12a — 18 = —6(2a + 3) Factorizar-6 .
b) ~2b3 + 6b2 - 18b = -2 b(b2 - 3b + 9) Factorizar-2b. #
L a n z a m ie n to d e u n a p e lo ta Cuandoselanzaunapelotahaciaarribaconunaveloci
dadde32piesporsegundodesdelapartemásaltade unedificiode160piesdealtu
ra, su distancia, d , respecto del piso en cualquier instante /, puede determinarse
mediantelafunciónd(t) = -16/2+32t + 160.
a) Determine ladistanciadelapelota respecto del piso despuésde3 segundos;es
decir,determined(3).
b) Factoriceel MFC del ladoderechode lafunción.
c) Evalúed(3) en laformafactorizada.
d) Comparesusrespuestasde laspartesa) y c).
a) d(t) = -1612 + 32/ + 160
d (3) = —16(3)2 + 32(3) + 160 Sustituya t por3.
= -16(9) +96 + 160
= 112
Ladistanciaes112pies.
b) Factorice -16 de lostrestérminosaladerechadel signo igual.
d(t) = -16(/2 - 2 1 - 10)
c) d(t) = -16(/2 - 2t - 10)
d (3) = —16[32 — 2(3) — 10] Sustituya t por3.
= -16(9 - 6 - 10)
= —16(—7)
= 112
d) Lasrespuestassoniguales. Puededeterminar loscálculosde lapartec) conmayor
facilidadque loscálculosde lapartea). #
3 Factorizar un factor binomial común
A lgunas veces la factorización exige factorizar un binomio com o el máximo factor co
m ún, com o se ilustra en los ejem plos 7 a 9.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-362-320.jpg)
![E J E M P L O 7 Factorice 3*(5* - 2 ) + 4(5* - 2 ).
Solución El M FC es (5* - 2). A l factorizar el M FC se obtiene
3 x (5 x - 2) + 4 (5* - 2) = (5* - 2) ( 3x + 4) #
E n el ejem plo 7, tam bién podríam os haber colocado el factor com ún a la d ere
cha p ara obtener
3* (5* - 2)+ 4 (5* - 2) = (3* + 4)(5* - 2)
Las form as factorizadas (5* - 2)(3* + 4) y (3* + 4)(5* - 2) son equivalentes de
acuerdo con la propiedad conm utativa d e la multiplicación,y am bas son correctas. Por
lo general, cuando listamos la respuesta a un ejem plo o ejercicio, colocam os el térm i
no com ún q u e se ha factorizado a la izquierda.
E J E M P L O 8 Factorice 9(2* - 5) + 6(2* - 5)2.
Solución EL M FC es 3(2* - 5). Reescriba cada térm ino com o producto del M FC y otro factor.
9(2* - 5) + 6(2* - 5)2 = 3(2* - 5) *3 + 3(2* - 5) *2(2* - 5)
= 3(2* — 5) [3 + 2(2* — 5 )] Factorizar 3(2* —5).
= 3 (2* — 5 )[3 + 4 * — 10] Propiedad distributiva.
= 3 (2* — 5 ) (4* — 7 ) Simplificar.
E J E M P L O 9 Factorice (2* - 5 )(a + b ) - (* - l)(fl + b).
S o l u c i ó n E l binom io a + b es el M FC d e los dos terrenos. Por lo tanto, lo factorizamos.
(2* - 5 )(a + ¿f) ~ (x ~ l ) ( a + b) = (a + b)[(2x - 5) - (* - 1)] Factorizar(a + b).
= (a + b )(2 * — 5 — * + 1) Simplificar.
AHORARESUELVAELEJERCICIO43 = (a + b ) ( x - 4) Factores. #
E J E M P L O 1 O Á rea E n la figura 5.13, el área del rectángulo grande es 7*(2* + 9 ),y el área del rec
tángulo pequeño es 3(2* + 9). D eterm ine una expresión, en form a factorizada, para
calcular la diferencia entre las áreas d e estos dos rectángulos.
Sección 5 .4 • Factorización del fa ctor c o m ú n d e los té rm inos d e un polinom io... • 3 3 5
A = 7*(2x + 9)
A = 3(2* + 9)
Solución Para determ inar la diferencia en tre las áreas, reste el área del rectán
gulo pequeño del área del rectángulo grande.
7 * (2 * + 9 ) - 3(2* + 9) Restariasáreas.
FIGURA 5.13
= (2* + 9 )(7 * — 3) Factorizar (2* + 9).
AHORARESUELVAELEJERCICIO 59 L a diferencia d e las áreas p ara los dos rectángulos es (2* + 9)(7* - 3).
4 Factorizar por agrupación
Cuando un polinom io contiene cuatro términos, es posible factorizarlo p o r agrupa
ción. Para factorizar por agrupación, quitam os los factores com unes d e grupos d e tér
minos. E ste procedim iento se ilustra en el siguiente ejemplo.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-363-320.jpg)



![Sección 5 .4 • Factorización del fa ctor c o m ú n d e los té rm inos d e un polinom io... • 3 3 9
Lea el ejercicio 69 antes de resolver los ejercicios 70 a 72.
70. Precio de un vestido El precio de un vestido se reduce en
10%, y luego se le aplica un nuevo descuento de 10%.
a) Escriba una expresión para calcular el precio final del
vestido.
b ) Cbmpare el precio final con el precio normal del ves
tido; ¿cómo son? Utilice factorización para obtener su
respuesta.
7L Precio de una segadora El precio de una segadora au
mentó 15%. Más tarde, en una venta especial, su precio se
redujo en 20%.
Rtctorice.
73. 5fl(3* - 2)5 + 4(3* - 2)4
75. 4*2(* - 3)3 - 6*(* - 3)2 + 4(* - 3)
77. ax2 + 2ax - 3 a + bx2+ 2bx - 3b
a) Escriba una expresión para calcular el precio final de
la segadora.
b) Compare el precio final con el precio normal; ¿cómo
s>n? Utilice factorización para obtener su respuesta.
72. Determinación deprecio ¿En cuál de las siguientes par
tes, a) o b),el precio final será menor y por cuanto?
a) Disminuya el precio de un artículo en 6% y luego au
méntelo en 8%.
b) Aumente el precio de un artículo en 6% y luego dis
minuyalo en 8%.
74 4p(2r - 3)7 - 3(2r - 3)6
76. 12(p + 2q)A - 40(p + 2q f + 12(p + 2q)2
78. 6a2 - a2c + 18a - 3ac + 6ab - abe
80. x2mn + *‘
82. r>'+4 + r y * 3 + r>+2
84. 6akbk - 2akck - 9bk + 3c*
.4mu
Rtclorice. Suponga que todas las variables de los exponentes representan números naturales.
79. **" - 2x4m
8L 3x4m - 2x3m + **"
83. arbr + ¿ V - ardr - <?dr
8 5 . a) ¿ó*3 —3x2 +9x = 3*(2*2 —* + 3)?
b) Si la factorización anterior es correcta, ¿cuál debe ser
el valor de 6*3 - 3*2 + 9* - f3*(2*2 - * + 3)] para
cualquier valor de *? Explique.
c) Seleccione un valor para * y evalúe la expresión de la
parte b). ¿Obtuvo loque esperaba? Si no,explique por
qué.
86. a) Determine si la siguiente factorización es correcta.
3(* - 2)2 - 6(x - 2) = 3(* - 2 ) [ ( x - 2) - 2]
= 3(x - 2 ) ( x - 4)
b) Si la factorización anterior es correcta, ¿cuál debe ser
el valor de 3(* - 2)2 - 6(* - 2) - [3(* - 2)(* - 4)J
para cualquier valor de*? Explique.
c) Seleccione un valor para * y evalúe la expresión de la
parte b). ¿Obtuvo loque esperaba? Si no,explique por
qué.
8 7 . Considere la factorización 8X3 - 16*2- 4* = 4*(2*2 - 4*
- i ) .
a) Sideterminamos
y , = 8*3 - 16*2 - 4*
= 4*(2*2 - 4* - 1)
y graficamos cada función, ¿qué debería suceder? Ex
plique.
b) En su calculadora graficadora, grafique y1y y2como se
dieron en la parte a).
c) ¿Obtuvo los resultados que esperaba?
d) Al verificar un procedimiento de factorización me
diante esta técnica, ¿qué significa si las gráficas no se
intersecan? Explique.
Considere la factorización 2*4 - ó*3 - 8*2 = 2*2(*2 -
3* - 4).
a) Introduzca
y! = 2*4 - 6*3 - 8*2
* = 2*2(*2 - 3* - 4)
en su calculadora.
b) Si utiliza la característicaTABLE de su calculadora, al
comparar la tabla de valores para y, con la tabla de va
lores para y2,¿qué esperaría? Explique.
c) Utilice la característicaTABLE para mostrar los valo
res de y, y y2 para valores de * de 0 a 6.
d) ¿Obtuvo los resultados que esperaba?
e) Cuando comprueba un proceso de factorización me
diante la característica TABLE, ¿qué significa que los
valores deyi y y2sean diferentes?
Ejercicios de repaso acumulativo
1 12
[1.4]
[2.1]
[3.1]
89. Evalúe . 2. ■
“ m *I si
90. Resuelva 3(2* - 4) + 3(* + 1) = 9.
91. Grafique y = ** —1.
[4.3] 92. Ejercicio Javier Bernal hace ejercicio todos los
días: camina a 3 mph y luego trota a 5 mph. Si tar
da 0.9 horas en recorrer un total de 3.5 millas,
¿cuánto tiempo trota?
[5.2] 93. Multiplique (7a - 3 ) (-2 a 2- 4a + 1).](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-367-320.jpg)








![A hora factorice x2 - x - 6.
= (x + 2 ){ x - 3)
Finalm ente, sustituya x con y2p ara obtener
= (y2 + 2 ) ( / - 3) Sustituir y2porx.
Así, y4 - y2 - 6 = (y2 + 2 ) ( / - 3). O bserve q u e y2se sustituyó p o r x, y después * se
sustituyó nuevam ente p o r y2. #
E J E M P L O 1 3 Factorice 3z4 - 17z 2 - 28.
Solución Sea * = z 2. Entonces el trinomio puede escribirse
3z4 - 17z2 - 28 = 3 (z2)2 - 17z2 - 28
= 3 / - 17x - 28 Sustituir z2porx.
= (3a: + 4 )(x — 7) Factorizar.
A hora sustituya x por z2.
- (3Z2 + 4JÍZ2 “ 7) S uet/tu/rjporz2.
AHORA RESUELVA EL E JER CIC IO 69 Así, 3z4 - 17z2 - 28 = (3z2 + 4 )(z2 - 7). #
E J E M P L O 1 4 Factorice 2 (a: + 5)2 - 5 (x + 5) - 12 .
Solución N uevam ente usarem os una sustitución, com o en los ejem plos 12 y 13. A l sustituir
a = x + 5 en la ecuación, obtenem os
2 (a: + 5 )2 - 5 (a: + 5) - 12
= 2a2 — 5a — 12 Sustituir(x + 5) pora.
A hora factorice 2a1 - 5a - 12.
= (2a + 3 ){a - 4)
Por últim o, reem place a con x + 5 p ara obtener
= [2(a: + 5) + 3][(a: + 5) — 4] Sustituirá por(x + 5).
= [2x + 10 + 3] [a: + 1]
= (2a: + 13) (a
: + 1)
Así, 2(a: + 5)2 - 5(a: + 5) - 12 = (2 a: + 13)(a: + 1). O bserve q u e a: + 5 se sustituyó
AHORA RESUELVA EL EJER CIC IO 7 3 po r a, y luego a p o r a: + 5 . #
E n los ejem plos 12 y 13 usamos x en nuestra sustitución, m ientras q u e en el ejem
plo 14 utilizam os a. L a letra seleccionada no afecta la respuesta final.
3 4 8 • C apítulo 5 • Polinom ios y fun cione s polinom iales
C o n j u n t o d e e j e r c i c i o s 5 . 5
Ejercicios conceptuales
L ¿Cuál debe ser siempre el primer paso para factorizar un
trinomio?
2. En un examen, Luis González escribió la siguiente facto
rización,pero el profesor la consideró incompleta. Expli
que por qué.
15*2 - 21* - 18 = (5* + 3)(3* - 6).
3. a) Explique paso a paso el procedimiento para factorizar
ó * 2 - * - 12.
b ) Factorice ó*2 - * - 12 mediante el procedimiento que
explicó en la parte a).
4. a) Explique paso a paso el procedimiento para factorizar
Sx2- 26* + 6.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-376-320.jpg)


![Sección 5 .6 • Fó rm u la s especiales de factorización • 3 5 1
115. Considerex2 + 2x - 8 = (x + 4 )(x - 2 ) .
a) Explique cómo puede comprobar esta factorización
mediante gráficas en su calculadora graficadora.
b) Compruebe si la factorización es correcta siguiendo el
procedimiento que explicó en la parte a).
Ejercicios de repaso acumulativo
a) Explique cómo puede comprobar esta factorización
utilizando la característicaTABLE de una calculadora
graficadora.
b) Cbmpruebe si la factorización es correcta siguiendo el
procedimiento que explicó en la parte a).
116. Cbnsidere dr’ - l l x 2 - 10* = x(2 x - 5)(3x + 2).
[2.2] 117. Resuelva F = j C + 32 para C.
[3.3] 118. Grafique y = -3 x + 4.
[4.5] 119. Evalúe el determinante
3 - 2 -1
2 3 - 2
1 - 4 1
[5.2] 120. Multiplique [ (x + y) + 5]2.
[5.3] 12L Factorice 2x3 + 4x2 - 5x - 10.
5 .6 F Ó R M U L A S E S P E C IA L E S D E F A C T O R IZ A C IÓ N
Ü ÉÉ
1 Factorizar la diferencia d e dos cuadrados.
2 Factorizar trinomios cuadrados perfectos.
3 Factorizar la sum a y la diferencia de dos cubos.
1 Factorizar la diferencia de dos cuadrados
E n esta sección se presentan algunas fórm ulas especiales para factorizar la diferencia
de dos cuadrados, trinomios cuadrados perfectos, y la sum a y diferencia d e dos cubos.
L e será d e utilidad m em o rizar estas fórmulas.
La expresión jc
2 - 9 es un ejem plo d e la diferencia d e dos cuadrados.
x 2 - 9 = (x ) 2 - (3 )2
Para factorizar la diferencia d e dos cuadrados,es conveniente usar la fórmula para la di
ferencia de dos cuadrados, misma q u e se analizó en la sección 5.2 cuando hablamos del
producto de la sum a y diferencia de los mismos dos térm inos (binomios conjugados).
Diferencia de d o s cu a d ra d o s
a2 - b2 = (a + b )(a - b)
E J E M P L O 1
Solución
E J E M P L O 2
Solución
Factorice las siguientes expresiones m ediante la fórm ula d e la diferencia d e dos cua
drados.
a) r 2 - 16 b) 25a:2 - 9 /
Reescriba cada expresión como una diferencia de dos cuadrados. Luego utilice la fórmula.
a) ¿ — 16 = (.x )2 ~ (4)2
= (x + 4 )(x - 4)
b) 25x2 - 9 y 2 = (5a:)2 - (3y )2
= (5x + 3 y ) ( 5 x - 3 y ) #
Factorice las siguientes diferencias d e cuadrados,
a) * 6 - y 4 b) 2 z4 ~ 162a:6
R eescriba cad a expresión com o una diferencia d e d o s cuadrados. Luego utilice la
fórm ula.
a) ¿ - / = (x3)2 - (y2)2
= ( x ¡ + ? ) { j ? - / )](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-379-320.jpg)
![3 5 2 • C apítulo 5 • Polinom ios y fun cione s polinom iales
b) 2 z4 - 162x6 = 2 (z4 ~ 81a:6)
= 2[(z2)2 - (9X3)2]
= 2(z2 + ftO í* 2 - 9X3) #
Factorice x4 - 16y4.
x 4 - 16y 4 = í*2)2 - (4y*)2
= (x2 + 4y2)(* 2 - 4 / )
O bserve q u e (x2 - 4y2) tam bién es una diferencia d e dos cuadrados. Utilice la fórm u
la d e la diferencia d e dos cuadrados una segunda vez p ara obtener
= (a 2 + 4y2)[(x )2 - (2y )2]
= ( x 2 + 4 / ) ( x + 2 y ) ( x - 2 y ) #
Factorice (* - 5)2 - 49 m ediante la fórm ula p ara la diferencia d e dos cuadrados.
Prim ero expresam os (* - 5)2 - 49 com o una diferencia d e dos cuadrados.
(x - 5 )2 - 49 = (x - 5 )2 - l 2
= [ ( * - 5 ) + ? ] [ ( * - 5 ) - 7 ]
= (x + 2 )(x - 12) #
Observación: No es posible factorizar la suma de dos cuadrados con la forma a2 + b2
en el conjunto de los números reales.
Por ejem plo, no es posible factorizar x2 + 4, ya q u e x2 + 4 = x2 + 22, es una su
m a d e dos cuadrados (y no una diferencia d e cuadrados).
2 Factorizar trinomios cuadrados perfectos
E n la sección 5.2, vimos que
(a + b )2 = a2 + 2ab + b2
(a ~ b )2 = a2 - 2ab + b2
Si invertim os los lados izquierdo y derecho d e estas dos fórm ulas, obtenem os dos
fórmulas especiales de factorización.
Trinom io s cu a d ra d o s p e rfe cto s
a2 + lab + b2 = (a + b)2
a2 - 2ab + b2 = (a - b)2
Estos dos trinom ios se denom inan trinomios cuadrados perfectos, ya q u e ca
d a uno es el cuadrado d e un binom io. Para ser un trinom io cuadrado perfecto, el p ri
m ero y el últim o térm inos debe ser el cuadrado de alguna expresión, y el térm ino
central debe ser eldoble delproducto delprimero y último términos. Cuando se le pida
factorizar un trinom io, determ ine si es un trinom io cuadrado perfecto antes d e inten
tar factorizarlo m ediante los procedim ientos explicados en la sección 5.5. Si es un
trinom io cuadrado perfecto, puede factorizarlo m ediante las fórm ulas indicadas con
anterioridad.
Ejemplos de trinomios cuadrados perfectos
y 1 + 6 y + 9 o y 2 + 2 (y )(3 ) + 32
9a2b2 - 24a b + 16 o (3ab)2 - 2(3aZ>)(4) + 42
(r + s ) 2 + 1 0(r + s) + 25 o {r + s)2 + 2(r + s)(5 ) + S2
A hora factoricem os algunos trinom ios cuadrados perfectos.
AHORA RESUELVA EL EJER CIC IO 17
E J E M P L O 3
Solución
E J E M P L O 4
Solución
AHORA RESUELVA EL EJER CIC IO 25](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-380-320.jpg)
![Sección 5 .6 • Fó rm u la s especiales d e factorización • 3 5 3
E J E M P L O 5
Solución
AHORA RESUELVA EL E JER CIC IO 29
E J E M P L O 6
Solución
E J E M P L O 7
Solución
AHORA RESUELVA EL E JER CIC IO 39
E J E M P L O 8
Solución
AHORA RESUELVA EL E JER CIC IO 45
E J E M P L O 9
Solución
Factorice x 2 - Sx + 16.
Com o el prim ero y último térm inos,*2y 42, son cuadrados, este trinom io podría ser un
trinom io cuadrado perfecto. Para determ inar si lo es, tom e el doble del producto d e *
y 4 para ver si obtiene 8*.
2 (* )(4 ) = 8*
Com o Sx es el térm ino central, y com o su signo es negativo, factorice com o sigue:
a2 - 8* + 16 = ( x ~ 4)2 #
Factorice 9a
:4 - 12*2 + 4.
E l prim er térm ino es un cuadrado, (3a2 )2, lo mismo q u e el último térm ino, 22. Com o
2(3x¿)(2) = 12a2, factorizam os com o sigue:
9x* - 1 2 a 2 + 4 = (3 a 2 — l f #
Factorice (a + b )2 + 6 (a + b) + 9.
E l prim er térm ino, (a + b)2,es un cuadrado. E l último térm ino, 9 o 32, también. E l tér
mino central es 2(a + b )(3 ) = 6(a + b). Por lo tanto,éste es un trinomio cuadrado p er
fecto. Así,
(a + b )2 + 6 (a + b ) + 9 = [(a + b) + 3]2 = (a + b + 3 )2 #
Factorice a2 - 6 a : + 9 - y 2.
Como a2 - 6a: + 9 es un trinomio cuadrado perfecto que puede expresarse com o (a: - 3)2,
escribim os
{x - 3)2 - /
A hora (a: - 3 )2 - y2 es una diferencia d e cuadrados; p o r lo tanto
( * - 3 ) 2 - y2 = [ ( x - 3 ) + y] [ ( x - 3 ) - y]
= ( x - 3 + y ) ( x - 3 - y )
Así, a2 - 6a: + 9 - y2 = {x - 3 + y )(x - 3 - y ) . #
El polinom io del ejem plo 8 tiene cuatro términos. E n la sección 5.4 aprendim os
a factorizar p o r agrupación los polinom ios con cuatro térm inos. Si analiza el ejem plo
8, verá q u e sin im portar cuánto se trate, los cuatro térm inos no pueden acom odarse de
m odo q u e tanto los prim eros dos térm inos com o los últim os dos tengan un factor co
mún. Siem pre q u e un polinom io con cuatro térm inos no pueda factorizarse p o r agru
pación, intente reescribir tres d e los térm inos com o el cuadrado d e un binomio, y luego
factorice m ediante la fórm ula d e la diferencia de dos cuadrados.
Factorice 4a2 + 12ab + 9b2 - 25.
Prim ero com probam os q u e este polinom io d e cuatro térm inos no puede factorizarse
p o r agrupación. Después, lo analizamos p ara determ inar si tres d e los térm inos q u e lo
conform an pueden expresarse com o el cuadrado d e un binomio. Ya q u e esto es posi
ble, escribim os los tres térm inos com o el cuadrado d e un binomio. P ara com pletar la
factorización, utilizam os la fórm ula d e la diferencia d e dos cuadrados.
4a2 + Ylab + 9b2 - 25 = (2a + 3b)2 - 52
= [(2a + 3b) + 5][(2a + 3b) - 5]
= (2a + 3b + 5 )(2a + 3b - 5 ) #](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-381-320.jpg)
![3 5 4 • Capítulo 5 • Polinomios y funciones polinomiales
3 Factorizar la suma y la diferencia de dos cubos
E JE M P L O 10
Solución
E J E M P L O 11
Solución
AHORA RESUELVA EL EJER CICIO 57
E JE M P L O 12
Solución
Al principio d e esta sección factorizam os la diferencia d e dos cuadrados. A hora fac-
torizarem os la sum a y la diferencia d e dos cubos. C onsidere el producto d e (a + b)
(a2 - ab + b2).
a2 - ab + b2
a + b
a2b - ab2 + b3
a3 - a2b + ab2
a 3 + b 3
Así, a3 + b3 = (a + b )(a 2 - ab + b2).Tam bién m ediante la multiplicación podem os
m ostrar q u e a3 - b3 = (a - b )(a 2 + ab + b2). Las fórm ulas p ara factorizar la sum a y
la diferencia de dos cubos aparecen en los siguientes recuadros.
S u m a d e d o s cu b o s
a3 + b3 = (a + b)(a2 - ab + b2)
Diferencia de d o s c u b o s
a3 - b3 = (a - b)(a2 + ab + b2)
Factorice x3 + 64.
Reescriba x 3 + 64 com o una sum a d e dos cubos, x 3 + 43. D eterm ine q u e x correspon
d a a a y 4 a b. Luego factorice m ediante la fórm ula d e la sum a d e dos cubos.
a3 + b3 = (a + b )(a 2 - a b + b2)
1 1 1 1 1 1 1 1
¿ + 43 = (* + 4 )[jc2 - x{4) + 4
2]
= (* + 4)(*2- 4x + 16)
A sí,*3 + 64 = (x + 4)(*2 - 4x + 16). #
Factorice 27X3 - 8y6.
Prim ero observam os q u e 27*3y 8y6 no tienen factores com unes distintos d e 1. Como
podem os expresar a 27*3y a 8y6com o cubos, podem os factorizar m ediante la fórm u
la para la diferencia de dos cubos.
27X3 - 8 / = (3 x)3 - ( 2 / f
= (3x - 2 /) [ ( 3 x ) 2 + ( 3 x ) ( 2 f ) + [ 2 / f ]
= (3* - 2y2){9x2 + 6xy* + 4y 4)
A sí, 21x3 - 8 / = (3x - 2y2)(9x2 + 6 x f + 4 / ) . #
Factorice 8 / - 6 4 /'.
Prim ero factorice 8, q u e es com ún a los dos términos.
8y3 - 64*6 = 8 { f - 8*6)
A hora factorice y3 - 8*0escribiéndolo com o una diferencia d e dos cubos.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-382-320.jpg)
![Sección 5 .6 • Fó rm u la s especiales d e factorización • 3 5 5
E JE M P L O 13
Solución
AHORARESUELVAELEJERCICIO 65
- 8*”) = q [ y y - ( Z rT J
= 8(y - 2x2) [ f + y (Ix 2) + ( Ix 2)2]
= 8( y - 2 x 2 ) ( y 2 + 2x 2 y + 4x4)
A sí,8 y2 - t o x 6 = 8 ( y - 2 x 2)(y2 + 2x2y + 4xi ). #
Factorice (x - 2)3 + 125.
Escriba (x - 2)3 + 125 com o una sum a de dos cubos; luego factorice utilizando la fór-
m uía p ara la sum a d e dos cubos.
(x - 2 Y + (5)3 = [(x - 2 ) + 5 ][(* - 2 )2 - (X - 2 ) (5) + (5)2]
= {x - 2 + SJÍx2 - 4x + 4 - 5* + 10 + 25)
= (* + 3)(x2- 9 x + 39) m
S U G E R E N C I A El cuadrado de un binomio tiene un 2 como parte del término central del trinomio.
(a + b)2 = a2 + la b + b2
(a ~ b)2 = a2 - la b + b1
La suma o la diferencia de dos cubos tiene un factor similar al del trinomio en el cuadrado
del binomio.Sin embargo, el término central no incluye un 2.
a3 + b3 = (a + b)(a2 - ab + b2)
a3 - b3 = (a - b)(a2 + ab + b2)
no es lab
EJ E M PL O 14 Volumen Utilizando los cubos d e la figura 5.16, determ ine una expresión, en form a
factorizada, p ara calcular la diferencia en tre sus volúmenes.
4*
FIGURA 5.16
Solución Para encontrar la diferencia en tre los volúmenes, reste el volum en del cubo pequeño
del volum en del cubo grande.
Volumen del cubo grande = (4*)3
Volumen del cubo pequeño = 33
Diferencia en tre los volúm enes = (4*)3- 33 te sta r volúmenes.
= (4x " 3)[(4x:)2 + (4*)3 + 3*] Factorizar.
= (4x - 3X16*2 + 12* + 9 ) Simplificar.
AHORA RESUELVA EL EJERCICIO 87 L a d ife re n c ia e n tr e lo s v o lú m e n e s d e los d o s c u b o s e s (4 * - 3 )(1 6 x* + 12* + 9 ). #
Cubo grande Cubo pequeño](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-383-320.jpg)


![Sección 5.7 • R e p a so general de factorización • 3 5 9
Reto
119. La expresión x6 - 1 puede factorizarse usando la dife
rencia de dos cuadrados o la diferencia de dos cubos. Al
principio los factores no parecen ser los mismos, pero
con un poco de manipulación algebraica puede demos
trarse que son iguales. Factorice x6 - 1 mediante a) la
diferencia de dos cuadrados, y b) la diferencia de dos cu
bos. c) Muestre que ambas respuestas son iguales, facto-
rizando completamente las respuestas obtenidas en la
parte a). Luego multiplique los dos binomios por los dos
trinomios.
O Actividad en equipo
Analice y responda en equipo el ejercicio 120.
120. Más adelante en el curso necesitaremos construir trino
mios cuadrados perfectos. Examinen algunos trinomios
cuadrados perfectos con coeficiente principal 1.
a) Expliquen cómo están relacionados b y c, si el trino
mio x2 + bx + c es un trinomio cuadrado perfecto.
Ejercicios de repaso acumulativo
b) Cbnstruyan un trinomio cuadrado perfecto, si los pri
meros dos términos son x1+ 6x.
c) Construyan un trinomio cuadrado perfecto, si los pri
meros dos términos son x2 -ÍO x.
d) Cbnstruyan un trinomio cuadrado perfecto, si los pri
meros dos términos son x2 -1 4 x.
[2.1] 121. Simplifique -2[3x - (2y - 1) - 5.r] + y. [5.4] 124 Factorice el máximo factor común de 45y12+ 30y10.
[3.6] 122. Si/)*) = ** - 3 í + 4 y g(x) = 2 x - 5 , determine l2S- Factorice U x2 - 9xy + 4xy - 3>2
.
( * - / ) ( - ! ) •
[4.4] 123. Ángulos Un ángulo recto se divide en tres ángulos
más pequeños. El más grande de los tres mide el do
ble del más pequeño. El ángulo restante mide 10°
más que el ángulo más pequeño. Determine la me
dida de cada ángulo.
5 . 7 R E P A S O G E N E R A L D E F A C T O R IZ A C IÓ N
8 m
1 F a c to riz a r p o lin o m io
1 Factorizar polinomios mediante una com binación d e técnicas.
>s m e d ia n te u n a c o m b in a c ió n d e té c n ic a s
H em os presentado varios m étodos p ara factorizar. A hora com binarem os problem as y
técnicas d e las secciones anteriores.
U n procedim iento general p ara factorizar cualquier polinom ios es el siguiente.
P a ra facto riza r un polinom io
L Determine si todos los términos del polinomio tienen un máximo factor común distin
to de 1.Si es así, factorice el MFC.
2. Siel polinomio tiene dos términos, determine si es una diferencia de dos cuadrados o
una suma o diferencia de dos cubos. En cualquiera de estos casos, factorice utilizando
la fórmula adecuada.
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-387-320.jpg)
![3 6 0 • C apítulo 5 • Polinom ios y fun cione s polinom iales
E J E M P L O 1
Solución
E J E M P L O 2
Solución
AHORA RESUELVA EL EJER CIC IO 27
E J E M P L O 3
Solución
E J E M P L O 4
Solución
E J E M P L O 5
Solución
AHORA RESUELVA EL EJER CIC IO 10
E J E M P L O 6
Solución
3. Si el polinomio tiene tres términos, determine si es un trinomio cuadrado perfecto. Si
lo es, factorícelo como corresponde. De lo contrario, factorice el trinomio utilizando
el método de prueba y error, por agrupación o por sustitución, como se explicó en la
sección 5.5.
4 Siel polinomio tiene más de tres términos, intente factorizarlo mediante agrupación. Si
eso no funciona, vea si tres de los términos son el cuadrado de un binomio.
5. Como paso final, examine el polinomio factorizado para ver si los factores enumera
dos tienen un factor común y se pueden factorizar más. Si encuentra un factor común,
factorícelo.
Los siguientes ejem plos ilustran cóm o utilizar este procedim iento.
Factorice 3x4 - 48 / .
Prim ero verifique si existe un máximo factor com ún distinto d e 1. Com o 3 / es com ún
a am bos térm inos, factorícelo.
3a:4 - 48a:2 = 3a:2(a:2 - 16) = 3 x 2(x + 4 )(* - 4)
O bserve q u e / - 16 se factoriza com o una diferencia d e dos cuadrados. #
Factorice 3 / / - 2 4 a:/ + 4 8 /.
Com ience factorizando el M FC, 3 / , de cada térm ino.
3a:2/ - 2 4 a :/ + 4 8 / = 3 / { x 2 - 8 x + 16) = 3y x - 4 )2
Observe q u e x2 - 8x +16 es un trinomio cuadrado perfecto. Si no lo reconoce, tam bién
podrá obtener la respuesta correcta factorizando el trinom io en (x - 4 )(x - 4). %
Factorice 2 4 / - 6xy + 16xy - 4 / .
Como siem pre,com ience p o r determ inar si todos los térm inos del polinom io tienen un
factor com ún. E n este ejem plo, el núm ero 2 es com ún a todos los términos. Factorice
el 2;después factorice el polinom io d e cuatro térm inos resultante m ediante agrupación.
24a:2 - 6 x y + 16xy - 4 / = 2(12a:2 - 3a:^ + 8 x y - 2y 2)
= 2[3x{4x - y ) + 2 y (4 x - y )]
= 2 (4a: - y )(3 x + 2y ) #
Factorice 1 0 /6 - 15ab + 206.
1 0 / 6 - 15ab + 206 = 5 6 ( 2 / - 3a + 4)
Com o 2a1 - 3 a + 4 no puede factorizarse, concluim os aquí. #
Factorice 2x4y + 54xy.
2x 4y + 54x y = 2 x y (x 3 + 27)
= 2 a :/a : + 3 ){ x 2 - 3 x + 9)
O bserve q u e factorizam os / + 27 com o una sum a d e dos cubos. #
Factorice 6x2 - 3 x + 6 / - 9.
Prim ero factorizamos el 3 d e los cuatro términos.
6a:2 - 3 x + 6 / - 9 = 3(2a:2 - a: + 2 / - 3)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-388-320.jpg)
![Se cció n 5.7 • R e p a so general de factorización • 361
A hora verem os si podem os factorizar los cuatro térm inos dentro d e los paréntesis m e
diante agrupación. Com o puede ver, esto no es posible, así q u e analizarem os si p ode
mos escribir tres d e los térm inos com o el cuadrado d e un binomio. Sin im portar cómo
los reordenem os, esto tam poco es posible. Concluim os q u e esta expresión no se p u e
d e factorizarse más. Por lo tanto,
6 x2 - 3 x + 6 y 2 - 9 = 3{2x2 - x + 2 y 2 - 3) #
E J E M P L O 7 F actorice3x* - 18* + 2 7 - 3 y 2.
Solución Factorizam os el 3 de los cuatro términos.
3 x2 - 18* + 27 - 3 / = 3 {x 2 - 6 x + 9 - y 2)
A hora intentarem os factorizar p o r agrupación. Com o los cuatro térm inos entre p a
réntesis no pueden factorizarse p o r este m étodo, veam os si podem os escribir tres de
los térm inos com o el cuadrado d e un binomio. Ya q u e esto sí es posible, expresam os
x2 ~ 6x + 9 com o (x - 3)2y después utilizam os la fórm ula p ara la diferencia d e dos
cuadrados. Así,
S x2 - 18* + 27 - 3 / = 3[(x - 3)2 - y 2]
= 3 [(* - 3 + y ) ( x - 3 - y ) ]
AHORA RESUEU/A EL EJER CICIO 4 3 = 3 {x ~ 3 + y ) { x ~ 3 ~ y ) #
SU G ER EN CIA
C 0 N 5 E J 0 P A R A
E 5 T U D I A R
En esta sección hemos repasado todas las técnicas para la factorización de expresiones.
Si todavía tiene problemas para factorizar, vuelva a estudiar el material de las seccio
nes 5.4 a 5.6.
C o n j u n t o d e e j e r c i c i o s 5 . 7
Ejercicios conceptuales
L Explique los procedimientos que pueden utilizarse para 2. ¿Cuál es el primer paso en el procedimiento de factori-
factorizar un polinomio de a) dos términos, b) trestérminos, zación ?
y c) cuatro términos.
Problemas de aplicación
Factorice completamente cada uno de los siguientes polinomios.
3. 3*2 - 75 4 3x2 - 24* + 48
£ 5. lOs2 + 19s - 15 6. 6 * y + io * v 3 + s*2/
7. —
8r2 + 26r - 15 8. 4*3 - 16*2 - 48*
9. 0.4*2 - 0.036 10. 0.5*2 - 0.08
1L 6x5 - 54* 12. l x 2y 2z 2 - 28*2^ 2
13. 3*6 - 3x5 + 12*5 - 12*4 14 2*2^ 2 + 6 * / - 10xy2 - 30y
15. 5 * V + 2 0 * Y + 15*3/ + 6 0 * Y 16. 6*2 - 15* - 9
£ 17. *4 - * y 18. 6*3 + 162
£
—
19. *y - * y 20. *4 - 81
2L *5 - 16* 22. i l x 2y 2 + 3 3 * / - 9 /
23. 2x6 + 1 6 / 24 8*4 - 4*3 - 4*3 + 2*2
25. 2(a + b f - 50 26. 12*3y2 + 4*2/ - 4 0 * /
£ 27. 6*2 + 36*y + 5 4 / 28. 3*2 - 30* + 75
£ 29. (x + 2)2 - 4 30. 4 / - 36x6](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-389-320.jpg)


![Ejercicios de repaso acumulativo
3 6 4 • C apítulo 5 • Polinom ios y fun cione s polinom iales
[2.1] 92. Resuelva 6{x + 4) - 4(3* + 3) = 6.
[2.6] 93. Determineel conjunto solución para
6 + 2 z
> 2 .
[4.3] 94. Mezcla decafés Aian Morales piensa abrir una tien
da de abarrotes, y desea mezclar 30 libras de café
para vender a un costo total de $170. Por obtener la
mezcla, utilizará café que vende a $5.20 por libra y
café que vende a $6.30 por libra. ¿Cuántas libras de
cada café debe utilizar?
[5.2] 95. Multiplique (Sx + 4)(*2 - x + 4).
[5.4] 96. Factorice Ix 3 + 4x2 - S x - 10.
5 . 8 E C U A C I O N E S P O L IN O M IA L E S
1 Usar la propiedad del factor nulo para resolver ecuaciones.
2 Usar la factorización para resolver ecuaciones.
3 Usar la factorización para resolver problem as de aplicación.
4 Usar la factorización para determ inar las intersecciones del eje
x d e una función cuadrática.
Siem pre q u e se establece q u e dos polinom ios son iguales entre sí, tenem os una ecua
ción polinomial.
Ejemplos d© ecuaciones polinomiales
x 2 + 2 x = x - 5
y 3 + 3 y - 2 = 0
4a:4 + 2 x 2 = - 3 x + 2
El g'ado de una ecuación polinomial esel mismo que el del término con mayor grado. Por
ejemplo, las tres ecuaciones anteriores tienen grados 2,3 y 4, respectivamente. Con frecuen
cia, una ecuación d e segundo grado con una variable se denom ina ecuación cuadrática.
Ejemplos de ecuaciones cuadráticas
3 X 2 + 6 x - 4 = 0
5 x = 2 x 2 - 4
( x + 4 )(x - 3) = 0
Cualquier ecuación cuadrática puede escribirse en la forma general.
Fo rm a ge n era l de u n a ecua ció n cu a d rá tica
ax2 + bx + c = 0, a * 0
donde a, b y c son números reales.
A ntes d e continuar, asegúrese d e q u e puede convertir cada una d e las tres ecua
ciones cuadráticas dadas anteriorm ente a su form a general, con a > 0.
1 U s a r la p ro p ie d a d d el fa c to r n u lo p a r a re s o lv e r e c u a c io n e s
P ara resolver ecuaciones utilizando factorización, em pleam os la propiedad del fac
tor nulo.
P ropiedad d el fa cto r nulo
Para todos los números reales a y b, sia •b = 0, entonces a = 0 o 6 = 0, o bien a y b = 0.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-392-320.jpg)





![3 7 0 • C apítulo 5 • Polinom ios y fun cione s polinom iales
Puede determ inar soluciones aproxim adas a ecuaciones cuadráticas q u e no son factorizables p o r m edio de
su calculadora graficadora. C onsidere el siguiente ejem plo d e la vida real.
E J E M P L O A n ten a s d e celulares E n E stados U nidos, el núm ero de antenas
repetidoras d e señales d e telefonía celular ha estado creciendo; entre 1996 y 2002, el
núm ero d e estas antenas, N , en miles, puede calcularse p o r medio d e la función
N ( t ) = -1 .4 5 t2 + 21.88* + 25.44
en donde t es el núm ero d e años desde 1996. D eterm ine el año en q u e el núm ero de
antenas repetidoras llegó a 80,000.
S o lu c ió n E n tie n d a e l p ro b le m a y tr a d u z c a Para responder esta pregunta
necesitam os q u e la función N (t) sea igual a 80, y despejar t.
-1 .4 5 12 + 21.88/ + 25.44 = 80 OitermlnarN(l) = 80.
No podem os resolver esta ecuación m ediante factorización, pero sí utilizando
una calculadora graficadora. Para hacerlo, denom inam os a un lado d e la ecuación y!
y al o tro y2.
y, = - í .4 5 x 2 + 21.88* + 25.44
>
■2 = 80
R ealice lo s c á lc u lo s A hora grafique las dos funciones en su calculadora grafica
dora y utilice las teclas T R A C E Z O O M u otras teclas (por ejem plo la tecla
C A L C con la opción 5yintersect, en la T I-8 3 Plus) p ara obtener su respuesta. La
[0,6,1,0,120,30]
FIGURA 5.22
figura 5.22 ilustra la pantalla de una T I-8 3 Plus, m ostrando q u e la coordenada x de
la intersección d e las ecuaciones está aproxim adam ente en x = 3.1520.
R e s p o n d a ftjr consiguiente,en 1999 (3 años a partir d e 1996) había casi 80,000 an
tenas repetidoras.
4 Utilizar la factorización para determinar las intersecciones del eje x
de una función cuadrática
Considere la gráfica d e la figura 5.23.
E n las intersecciones del eje x , el valor d e la función, o y, es 0. A sí, si desea
m os determ inar las intersecciones del eje x d e una gráfica, podem os establecer la
función = Oy despejar x.
E J E M P L O 10 D eterm ine las intersecciones del eje x de la gráfica q u e se obtiene al graficar y = x2 -
2x -8 .
Solución E n las intersecciones del eje x , y tiene un valor d e 0. Por lo tanto, para determ inar las
y * intersecciones del eje x escribim os
x 2 ~ 2 x - 8 = 0
(x ~ 4 ) ( x + 2 ) = 0
x — 4 = 0 o * + 2 = 0
* = 4 x = - 2
Las soluciones d e x2 - 2x - 8 = 0, son 4 y -2 . Las intersecciones del eje * de la grá
fica que se obtiene d e y = x2 - 2x - 8son ( -2 ,0 ) y (4,0),como se ilustra en la figura 5.24.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-398-320.jpg)
![Sección 5 .8 • E c u a c io n e s polinom iales • 3 7 1
FIGURA 5.24
AHORA RESUEU/A EL E JER CIC IO 75
Si conocem os las intersecciones del eje a:de una gráfica, podem os determ inar la
ecuación d e la gráfica. L ea el siguiente recuadro p ara aprender cóm o hacerlo con ayu
d a d e su calculadora graficadora.
Cómo utilizar su calculadora graficadora
E n el ejem plo 10 vimos q u e la gráfica q u e se obtuvo d e y = x L- 2 x - 8 tenía las intersecciones del eje a: en
- 2 y 4. Si conocem os las intersecciones del eje x de una gráfica,podem os determ inar ecuaciones cuyas gráficas sean
esas intersecciones. Por ejemplo,
Intersecciones
del eje a: en Factores Ecuación
- 2 y 4 (x + 2 )(x - 4) y = (x + 2)(a: - 4)
o y = x 2 - 2 x - 8
Ténga en cuenta q u e otras ecuaciones pueden tener gráficas con las mismas intersecciones del eje a:. Por ejem plo,
la gráfica d e y = 2(a^ - 2a: - 8 ) o y = Ix2 - 4x - 16 d a p o r resultado gráficas q u e tam bién tienen intersecciones
del eje a: en 4 y - 2 . D e hecho, la gráfica d e y = a f é - 2x - 8), p ara cualquier núm ero real distinto d e cero a, ten
d rá intercepciones del eje a: en 4 y -2 .
C onsidere la gráfica d e la figura 5.25.
[ - 10,10,1, - 10,20,2]
FIGURA 5.25 FIGURA 5.26
Si suponem os q u e las intersecciones son valores enteros, las intersecciones del eje a
: están en 2 y 8. Por con
siguiente,
Intersecciones
del eje x en Factores Ecuación
2 y 8
i
S
i
1
00
y = ( x - 2)(x - 8)
o y = x 2 - 1 0 a : + 16
Si cam biam os la ventana,vem os q u e la intersección del eje y de la gráfica está en 16 (vea la figura 5.26). Por lo tan
t o ^ = x2 - 10a: + 16 podría ser la ecuación q u e dio lugar a la gráfica. Si, p o r ejem plo, la intersección del eje y de
la gráfica estuviese en 32, entonces la ecuación d e la gráfica podría ser y = 2(x2 - 10a: + 16) o y = Ix 2 - 20x + 32.
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-399-320.jpg)




![3 7 6 • C apítulo 5 • Polinom ios y fun cione s polinom iales
117. Cbnsidere la gráfica siguiente de una función cuadrática.
y
118.
a) Escriba una función cuadrática que tenga las intersec
ciones del eje x indicadas.
b) Escriba una ecuación cuadrática con una variable cuya
salución sea - 2 y -5.
c) ¿Cuántas funciones cuadráticas diferentes pueden te
ner intersecciones del eje x de - 2 y -5? Explique.
d) ¿Cuántas ecuaciones cuadráticas diferentes con una va
riable pueden tenersoluciones de - 2 y -5? Explique.
Lagráfica de laecuacióny = x2 + 4se ilustra acontinuación.
a) ¿Cuántas intersecciones del eje x tiene la gráfica?
b) ¿Cuántas soluciones reales tiene la ecuación x2 + 4 = 0?
Explique su respuesta.
119. Cbnsidere la función cuadrática
P(x) = ax2 + bx + c,a > 0.
a) La gráfica de este tipo de función puede no tener inter
secciones del eje x, una intersección del eje x o dos in
tersecciones del eje x. Bosqueje cada una de estas
posibilidades.
b) ¿Cuántas posibles soluciones reales puede tener la
ecuación ax1+ bx + c = 0,a > 0! Explique su respues
ta a la parte b) utilizando los bosquejos de la parte a).
120. Distanciapara detenerse Ladistancia, d en pies,para de
tener un automóvil común que viaja sobre pavimento se
co puede calcularse mediante la función d(s) = 0.034s2 +
0.56s - 17.11,en donde s es la velocidad del automóvil an
tes de frenar y 60 =2s ^ 80 millas por hora. Si un automó
vil requiere de 190pies para detenerse después de aplicar
tos frenos, ¿qué tan rápido va el automóvil?
12L Distanciapara detenerse Ladistancia, d en pies, para de
tener un automóvil común que viaja sobre pavimento mo
jado puede calcularse mediante la función d(s) = -0.031S2
+ 59.82s - 2180.22, en donde s es la velocidad del auto
móvil antes de frenar y 60 < s < 80 millas por hora. Si un
automóvil requiere de 545 pies para detenerse después de
aplicar los frenos, ¿qué tan rápido va el automóvil?
Reto
Resuelva*
122. x4 - 5x2 + 4 = 0 123. x4 - 13x2 = -3 6 124 x6 - 9X3 + 8 = 0
2. Actividad en equipo
En cursos más avanzados de matemáticas podría necesitar despejar y' (se lee “
y prima”) en una ecuación. Cuando esto ocurra, trate
a y' como una variable diferente de y De forma individual despeje y' de cada ecuación. En equipo, compare sus respuestas y obtenga
las respuestas correctas.
125. xy' + yy ' = 1 126. xy - xy ' = 3y ' + 2 127. 2x y y ' - x y = x - 3y'
Ejercicios de repaso acumulativo
[1.5] 128. Simplifique (4x“2y3)”2. [4.1] 130. Resuelva el sistema de ecuaciones
[2.5] 129. Resuelva la desigualdad y grafique la solución en 3x + 4y = 2
la recta numérica. 2x = - 5 y —1
[5.2] 131. Si f(x) = - x 2 + 3x y g
< 4 (3 * _ -2 ) ^ 5 ( f .g)(4).
[5.7] 132. Factorice (x + 1) — (x + 1 ) — 6.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-404-320.jpg)

![3 7 8 • C a p ít u lo 5 • P o lin o m io s y f u n c io n e s p o lin o m ia le s
F o r m a g e n e r a l d e u n a e c u a c i ó n c u a d r á t i c a : ax? + bx + c = 0, a # 0.
P r o p i e d a d d e l f a c t o r n u lo : Si a • b = 0 , entonces a = 0 o b = 0 ,o am bos a y b = 0.
T e o r e m a d e P i t á g o r a s :
cateto2 + cateto2 = hipotenusa2o a2 + b2 = c¿.
a
Ejercicios de repaso del capítulo
[5.1] Determine si cada expresión es un polinomio. Si la expresión es un polinomio, a) proporcione el nombre especial del polino
mio, si lo tiene, b)escriba el polinomio en orden descendente de la variable x, y c) indique el grado del polinomio.
L 3x2 + 2
3. 8a: - x"1 + 6
Realice cada operación indicada.
5. (x 2 - 5x + 6) + (2x + 3)
7. (2a - 3b - 2) - ( - a + 5b - 8 )
9. (3x 2y + 6xy - 5y 2) - (4y 2 + 3a:>-)
11. Sume x2- 3x + 5 con 4x*2 + l(k - 9.
13. Determine P ^ . s i P(x) =2x2 - 3 x + 13.
2. 5a: + 4a:3 - 9
4. - 3 - 10*2y + 6xy3 + 2xA
6. ( lx 2 + 2 x - 5) - (2a:2 - 9 x - 1)
8. (4a:3- 4a:2- 2a:) + (2 a3 + 4a:2- 7a: + 10)
10. (-8 a b + 2b2 - 3 a ) + ( - b 2 + 5ab + a)
12. Reste 3a1b - 5ab de -7 a2/» - ab.
14 Determine P(-3 ), si P(x) = x3 - 3 X 2 + 4x - 9.
En los ejercicios 15 y 16, determine una expresión polinomialpara calcular el perímetro de cada figura.
15. , . ^ 16. _ ^ + 7
, x 2 + 1 13a
: + 8
A^ + 2r
En ¡os ejercicios17y 18de la página 379, utilizamos la siguiente gráfica, en donde semuestran los ingresos y egresos de laAdministración de
Seguridad Social de Estados Unidos entre 1997y 2025.
Ingresos y egresos de seguridad social
$2000j
| $1600
% $1200
1
$800
$400
97 98 99 00 01 02 03 Ot 05 06 10 15 20 25
Año
Fuente: A dm inistración d e S egundad Social de Estados Unidos](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-406-320.jpg)
![Ejercicios de re p a so del capítulo • 3 7 9
17. Ingresos en seguridad social La función R(¡) = 0.78/2 +
20.28/ + 385.0, en donde / representa los años desde 1997
y 0 ^ / ^ 28,sirve para calcular los ingresos aproximados
que genera la industria de la seguridad social en Esta
dos Unidos,/?(/), en miles de millones de dólares.
a) Mediante la función proporcionada, estime los ingresos
en 2010.
b) Cbmpare su respuesta en la parte a) con la gráfica en
la página 378. ¿La gráfica apoya su respuesta?
[5.2] Multiplique.
19. 2x(3x2 - I x + 5)
2L (3x - 5){2x + 1)
23. (x + 8y)2
25. (2xy - l)(5x + 4y)
TI. (2a + 9 b f
29. ( I x + 5y)(7x - 5y)
31. (5xy + 6)(5xy - 6)
33. [(x + 3y) + 2]2
35. (3x2 + 4x - 6)(2x - 3)
18. Egresos en seguridad social La función G(t) = 1.74/2 +
7.32i + 383.91, en donde / representa años desde 1997 y
0 < / < 28, sirve para calcular los egresos de la industria
de seguridad social, G(/),en miles de millones de dólares.
a) Mediante la función proporcionada, estime los egresos
en 2010.
b) Campare su respuesta de la parte a) con la gráfica en
la página 378. ¿La gráfica apoya su respuesta?
20. - 3 x / ( x 3 + xy4 - 6y5)
22. (5a + 9)( 10a - 3)
24. (a - 11b)2
26. (2pq - r)(3pq + Ir)
28. (3x - 2y)2
30. (2a - 5b2)(2a + 5b2)
32. (9a2 - 2b2)(9a2 + 2b2)
34. [(2p - q ) - 5]2
36. (4x3 + 6x - 5)(x + 3)
En los ejercicios 37 y 38, determine una expresión para calcular el área total de cada figura.
37. 38.
ñtra cada par de funciones, determine a) ( f •g) (x) y b) ( f ‘ g)(3).
39. f ( x ) = x + 2,g (x ) = x - 3
4L f ( x ) = x2 + x - 3, g (x) = x - 2
[5.3] Divida.
6x2 + 9x + 12
43.
45.
47.
21y3 + 6y + 2
4x3y2 + 8x2y3 + 12xy4
8xy3
4 9 . (2x4 - 3x3 + 4X2 + 17x + 7) + (2x + 1)
5L (x2 + x - 18) + (x - 3)
40 . f ( x ) = 2x - 4 , g(x) = x2 - 3
42 . f ( x ) = x2 - 2,g (x ) = x2 + 2
44.
46.
l a 2 - 1 6 a + 2 0
45pq - 2 5 c f - 10q
48. (8x2 + 14x - 15) + (2x + 5)
50. (4a4 - la 2 - 5a + 4) + (2a - 1)
52. (4x3 + 12x2 + x - 10) + (2x + 3)
Utilice la división sintéticapara obtener el cociente de cada expresión.
53. (3x3 - 2x2 + 10) + (x - 3) 54. (2y5 - 10y3 + y - 1) + (y + 1)
55. ( í s - 20) + (jc - 2) 56. {2x3 + *2 + 5jt - 3 ) (jr - i )
Determine el residuo de cada división mediante el teorema del residuo. Si el divisor es un factor del dividendo, indiquelo.
57. (x2 - 4x + 11) + (x - 3) 58. (2x3 - 6x2 + 3x) + (x + 4)
59. (3*3 - 6) -5
- ( x - j ) 60. (2x‘ - 6x2 - 8) *• (x + 2)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-407-320.jpg)
![3 8 0 • C apítulo 5 • Polinom ios y fun cione s polinom iales
[5.4] En cada expresión, factorice el máximo factor común.
61. 4*2 + 8* + 24
63. 10a3¿>
3 - 12a2b6
Factoricepor agrupación.
65. 5*2 - x y + 20xy - 4 /
67. (2x - 3)(2x + 1) - (2* - 3)(x - 8)
62. 15*4 + 6*3 - 12*4/
64. 12*yV + 6*2/ z2 - 15x 3y V
66. 12a2 - 8 a b + 15ab - 10b2
68. 7*(3* - 5) + 3(3* - 5)2
En los ejercicios 69 y 70, A representa el área de la figura. Determine una expresión en forma factorizada, para calcular la diferencia
entrelas áreas de lasfiguras geométricas.
69.
A = 13*(5* + 2)
70.
I
A = 7(5* + 2)
A = 14*2+ 18* A = 7* + 9
En los ejercicios 71 y 72, V representa el volumen de la figura. Determine una expresión, en forma factorizada, para calcular la dife
rencia entre los volúmenes de lasfiguras geométricas.
e
y = 7(17*+ 3)
[5.5] Factorice cada trinomio.
73. / + 8* + 12
75. / - 4* - 21
77. - * 2 + 12* + 45
79. 2*3 + 13*2 + 6*
81. 4a3 - 9a2 + 5a
83. / - 15xy - 54y2
85. *4 + 8*2 + 15
87. (* + 5)2 + 10(* + 5) + 24
72.
©
V = 20x2 + 25x V = 8x+10
74. *2 + 2* - 15
76. *2 - 10* + 16
78. - * 2 + 13* - 12
80. 8*3 + 10*2 - 25*
82. 1 2 / + 6 1 / + 5 /
84. 6p2 - 19p q + 1 0 /
86. *4 + 2*2 - 63
88. ( * - 2 )2 - ( * - 2) - 20
En los ejercicios 89 y 90, determine una expresión, en forma factorizada, para calcular el área de la región sombreada en cada figura.
89. 90.
x + 2
x + 9
x + 4
[5.6] Utilice unafórmula especial defactorización parafactorizar las siguientes expresiones.
91. x2 - 49 92. *2 - 100
93. *4 - 16 94 *4 - 81
95. 4a2 + 4a + 1 96. 4 / - 12y + 9
97. (* + 2)2 - 9 98. (3y - l) 2 - 25](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-408-320.jpg)
![Ejercicios de re p a so del capítulo • 381
99. p* + 16p2 + 64 100. bA - 14b2 + 49
101. *2 + 8* + 16 - y 2 102. a2 + 6ab + 9b2 - 4c2
103. 9*2 + 6xy + y 2 104. 36b2 - 60bc + 25c2
105. *3 - 27 106. / + 64
107. 125*3 - 1 108. 8a3 - 21b3
109. (* + l) 3 - 8 110. (* - 2)3 - 27
111. y 3 - 6 4 / 112. (a + 3)3 + 1
En los ejercicios113 y 114, determine una expresión, en formafactorizada, para calcularel área de la región sombreada en cadafigura.
113.
115. Volumen Determine una expresión, en forma factoriza
da, para calcular la diferencia entre los volúmenes de es
tos dos cubos.
116. Volumen Determine una expresión, en forma factoriza
da, para calcular el volumen de la región sombreada de
esta figura.
[5.4-5.7] Factorice completamente.
117. x 2/ - 2xy2 - 15y 2
119. 3*3/ + 18*y - 6X2/ - 3 6 * /
121. 2x3y + 16y
123. 6*3 - 21x2 - 12*
125. 3*3 + 2 4 /
127. 4(2* + 3)2 - 12(2* + 3) + 5
129. (* - l) * 2 - (* - 1 )* - 2(x - 1)
131. 6p 2q2 - Spq - 6
133. 4y 2 - (* 2 + 4* + 4)
135. 6*4/ + 9*3/ - 27* Y
a c
118. 3*3 - 18*2 + 24*
120. 3y5- 27y
122. 5x*y + 20x 3y + 20*2y
124. *2 + 10* + 25 - /
126. *2(* + 4 ) + 3 * (* + 4 ) - 4 (x + 4)
128. 4*4 + 4*2 - 3
130. 9ax - 3 bx + 12ay - 4by
132. 9*4 - 12*2 + 4
134. 6(2a + 3 )2 - 7 (2 a + 3 ) - 3
^ x 3 " ^ f y6
Área En los ejercicios 137 a 142, determine una expresión, en forma factorizada, para calcular el área de la región sombreada
de cada figura.
137.
y + 7](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-409-320.jpg)
![3 8 2 • C apítulo 5 • Polinom ios y fun cione s polinom iales
139.
b ¿
>
h b
b b
b
140.
b b
14L
a + 3b
a b a b
ü
142.
a
a a
b
[5.8] Resuelva..
143. (x - 3)(4* + 1) = 0
146. 15*2 + 20* = 0
149. x2 = 8x - 7
152. 20/t2 - 6 = 7p
144. (2 * + 5)(3* + 7) = 0
147. j*2 + Ix + 12 = 0
150. c3 - 6c2 + 8c = 0
153. 5*2 = 20
145.
148.
2x2 = 4*
a2 + a - 30 = 0
151. 12d2 = 13d + 4
154. x (x + 3) = 2(x + 4) - 2
íM/ce factorización para determinar las intersecciones del eje x de la gráfica de cada ecuación.
155. y = 2x2 - 2x - 60 156. y = 20*2 - 49* + 30
Escriba una ecuación cuya gráfica tenga las intersecciones del eje x en los valores dados.
3 5
157. - 3 y 6
“ *
• - F - 6
En los ejercicios 159 a 163, responda la pregunta.
159. Alfombra El área de una alfombra rectangular es de 99
piescuadrados. Determine el largo y ancho de la alfombra,
si el largo es 2 pies mayor que el ancho.
160. Anuncio triangular La base de un anuncio triangular mi
de 3 pies más que el doble de la altura. Determine la base
y la altura, si el área del triángulo es 22 pies cuadrados.
161. Cuadrado Un cuadrado tiene un lado de 4 pulgadas ma
yorque el lado de un segundo cuadrado. Siel área del cua
cad o más grande es de 49 pulgadas cuadradas,determine
la longitud de cada lado de ambos cuadrados.
162. Velocidad Un proyectil es lanzado hacia arriba, desde la
parte más alta de un edificio de 144 pies de altura, con una
velocidadde 128pies porsegundo. La distancia del proyec
til respecto del suelo en cualquier instante /, en segundos,
está dada mediante la fórmula s(/) = -161
2 + 128/ + 144.
Determine el tiempo que tarda el proyectil en estrellarse
contra el suelo.
163. Postes telefónicos Sesujetan dos cables tensados a un pos
te telefónico para ayudar a estabilizarlo. El cable se suje
ta a * pies de la base del poste, sobre el suelo. La altura
del poste es * + 31 y el largo del cable es * + 32. Deter
mine *.](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-410-320.jpg)

![E x a m e n d e r e p a s o a c u m u la t iv o
3Q A • C apítulo 5 • Polinom ios y funcion e s polinom iales
Resuelva el examen y verifique sus respuestas con las que aparecen al final. Revise las preguntas que haya respondido incorrecta
mente. Los números de la sección y el objetivo en donde se analiza el material correspondiente se indican después de cada respuesta.
L Determine A U B para A = {2,4,6,8} y B = (3,5,6,8}.
2. Ilustre {r|x ^ -5} en la recta de los números reales.
3. Divida + (-2 ).
4 Evalúe ( -3 )3 - 22 - ( - 2 ) 2 + (7 - 7)2.
implifique [ y -
2 rV Y
5. Simplifique { 2 . .
6. Resuelva 4(2* —2) —3(* + 7) = —
4.
7. Resuelva k =2(d + e) para e.
8. Terreno Un arquitecto desea cercardos áreas iguales, co
mo se ilustra en la figura. Si ambas áreas son cuadrados y
el largo total de la cerca utilizada es de 91 metros, deter
mine las dimensiones de cada cuadrado.
9. Copias Cecilia Sánchez tiene un manuscrito y necesita
obtener 6 copias del mismo antes de enviárselo a un edi
tor en Argentina. La primera copia cuesta 15 centavos por
página y cada copia adicional cuesta 5 centavos por pági
na. Si el pago total es de $248, ¿cuántas páginas tiene el
manuscrito?
10. Promedio de calificaciones Las primeras cuatro califi
caciones que obtuvo Luis Ruiz en sus exámenes son 68,
72, 90 y 86. ¿Qué rango de calificaciones de su quinto
examen producirá un promedio mayor o igual que 70 y
menor que 80?
IL ¿(4,1) es una solución de la ecuación 3x + 2y = 9?
12. Escriba la ecuación 2 = 6x - 3y en la forma general.
13. Determine la pendiente de la línea que pasa por los pun
tos (8, —
4) y ( —
1 , - 2).
14 Sif{x) = 2x* - 4X2 + x - 16,determine/(-4 ).
15. Grafique la desigualdad 2x - y ^ 6.
16. Resuelva el sistema de ecuaciones.
2 8
r - y = 3
17. Resuelva el sistema de ecuaciones.
x - 2 y = 2
2x + 3y = 11
- y + 4z = 7
18. Evalúe el determinante.
7 3
- 2 1
19. Divida (2x3 - 9 x + 15) - (x - 6).
20. Factorice 64.r’ - 27y3.
R e s p u e s t a s a l e x a m e n d e r e p a s o a c u m u la t iv o
-5 16
4 - 3 5 ; [Sec. 1.4,O bj.3] 5 .8 rV s;[Sec. 1.5,Obj.7] 6.5; [Sec. 2.1,Obj. 3) 7.e = - ~ — ; [Sec.2 2 ,Obj.2]
13 metros; [Sec. 2.3, Obj. 2] 9.620 páginas; [Sec. 2.3, Obj. 2] 10.34 £ * < 84; [Sec. 2.5,Obj. 3] 11. No;
12.6* - 3y = 2; [Sec. 3.3, Obj. 2] 13. - 1 ; [Sec. 3.4, Obj. 2] 14. - 212; [Sec. 3.6, Obj. 1] 15. y
[Sec. 3.7, Obj. 1] 16. (10, 4); [Sec.4.1, Obj. 3] 17. (4,1,2); [Sec. 42, Obj. 1] 2;
393
18.13; [Sec.4.5, Obj. 1] 19.2*2 + 12* + 63 + [Sec. 5.3, Obj. 2] M M l_
20. (4* - 3y)(16*2 + 12*y + 9y 2); [Sec. 5.6, Obj. 3] " 2I
-4 -
i
Obj. 5]
8. 13 metros por
Sec.3.1,Obj. 2]
1 1/ l 1
----í
- Y 4 x](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-412-320.jpg)











![3 9 6 • C apítulo 6 • Expresiones racionales y e cu a cio n e s
111. Cbn base en la función racional f ( x ) - —.
a) Determine el dominio de la función.
b) Cúmplete la siguiente tabla.
X -1 0 - i -0.5 -0.1 -0.01 0.01 0.1 0.5 1 10
y
c) Trace la gráfica de f ( x) = —. Indique qué le sucede a
x
la función conforme x se aproxima a 0, tanto por la
izquierda como por la derecha.
d) ¿Esta gráfica puede tener un valor de 0? Explique su
respuesta.
Actividad en equipo
112. Analicen la función racional f ( x ) =
x2 - 4
x - 2
a) Determinen en equipo su dominio.
b) De manera individual cada miembro del equipo com
plete la siguiente tabla para la función.
x - 2 -1 0 1 1.9 1.99 2.01 2.1 3 4 5 6
y
c) Cbmparen sus respuestas a la parte b),y pónganse de
acuerdo acerca de cuáles son los valores correctos de
la tabla.
x 2 — 4
d) Tracen en equipo la gráfica de f ( x) = — — r-. ¿La
x ¿
función está definida cuando x = 2?
e) ¿Esta gráfica puede tener algún valor de 0? Si es así,
¿para qué valor o valores de a es f(a) = 0?
Ejercicios de repaso acumulativo
[2.2] 113. Despeje y de 3(x - 2) + 3y = 6x.
4x
[2.5] 114 Resuelva 4 + — < 6 y proporcione la respuesta
en notación de intervalo.
2x - 4
[2.6] 115. Resuelva = 12.
[3.2] 116. Sea f{x) = |6 - 3x| - 2 Determine/(1.3).
[4.1] 117. Resuelva el sistema de ecuaciones.
3x + 4y = 2
2x + 5y = - 1
[5.6] 118. Factorice 9X2 - 6xy + y2 - 4.
6 . 2 S U M A Y R E S T A D E E X P R E S IO N E S R A C IO N A L E S
i ÉÉ
1 Sum ar y restar expresiones con un denom inador com ún.
2 Determinar el mínimo com ún denom inador (M C D ).
3 Sum ar y restar expresiones sin denom inadores com unes.
4. Analizar aplicaciones de expresiones racionales.
1 S u m a r y re s ta r e x p re s io n e s c o n u n d e n o m in a d o r c o m ú n
A l sum ar (o restar) dos expresiones racionales con un com ún denom inador,sum am os
(o restam os) los num eradores y conservam os el denom inador común.
P a ra su m a r o re s ta r e xp re sio n e s racionales
Para sumar o restar expresiones racionales, utilice las siguientes reglas.
Suma R e sta
c * 0 c * 0
c c c c c c
(continúa en la página siguiente)](https://image.slidesharecdn.com/lgebraintermedia-angel-06-220626050109-21023f4e/85/Algebra-Intermedia-Angel-06-pdf-424-320.jpg)