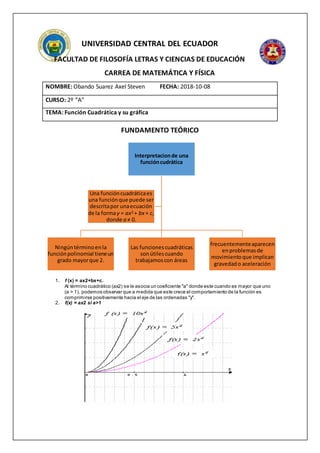
1. Las funciones cuadráticas se representan por la ecuación f(x)=ax^2+bx+c, donde el término cuadrático ax^2 determina la forma de la parábola. Un valor de a mayor que 1 comprime la parábola positivamente hacia el eje y. 2. Las funciones cuadráticas son útiles para trabajar con áreas y aparecen comúnmente en problemas de movimiento que implican gravedad y aceleración. 3. El método de mínimos cuadrados permite encontrar la recta de mejor ajuste a un conjunto

1. UNIVERSIDAD CENTRAL DEL ECUADOR
FACULTAD DE FILOSOFÍA LETRAS Y CIENCIAS DE EDUCACIÓN
CARREA DE MATEMÁTICA Y FÍSICA
NOMBRE: Obando Suarez Axel Steven FECHA: 2018-10-08
CURSO: 2º “A”
TEMA: Función Cuadrática y su gráfica
FUNDAMENTO TEÓRICO
1. f (x) = ax2+bx+c.
Al término cuadrático (ax2) se le asocia un coeficiente "a" donde este cuando es mayor que uno
(a > 1), podemos observar que a medida que este crece el comportamiento de la función es
comprimirse positivamente hacia el eje de las ordenadas "y".
2. f(x) = ax2 si a>1
Interpretacionde una
funcióncudràtica
Ningúntérminoenla
funciónpolinomial tieneun
grado mayorque 2.
Las funcionescuadráticas
sonútilescuando
trabajamoscon áreas
frecuentementeaparecen
enproblemasde
movimientoque implican
gravedado aceleración
Una funcióncuadráticaes
una funciónque puede ser
descritapor unaecuación
de la formay = ax2 + bx + c,
donde a ≠ 0.

2. Método Linealización
Una forma Más Precisa de ENCONTRAR La Recta Que mejor se
ajusta es el Método de Mínimos Cuadrados .
Utilice Los Pasos Siguientes párrafo ENCONTRAR La ecuación de la
recta Que mejor se ajusta PARA UN conjunto de parejas ordenadas .
Paso 1: Calcule la media de los Valores de x y la Media de los
Valores de y .
Paso 2: Realice La Suma de los Cuadrados de los Valores de x .
Paso 3: Realice La Suma de Cada valor de x multiplicado por su
valor Correspondiente y .
Paso 4: Calcule la pendiente de la recta Usando la fórmula:
Donde n es El Número El total de los Puntos de Datos.
Paso 5: Calcule la intercepción en y de la recta Usando la fórmula:
Donde hijo las medias de las COORDENADAS de xy y de los
Puntos de Datos respectivamente.
Paso 6: Uso de La Pendiente y La intercepción en y para Formar la
ecuación de la recta.

3. 𝑃1
𝑇1
=
𝑃2
𝑇2
Bibliografía:
http://www.monografias.com/trabajos100/matematicas-funciones-y-tipos-
funciones/matematicas-funciones-y-tipos-funciones.shtml
http://www.vitutor.com/geo/rec/d_5.html
http://recursostic.educacion.es/descartes/web/materiales_didacticos/vectores_rectas_plano_
alm/index/rectageneral.htm
Obtención de la ecuación de una
función cuadrática
Ecuación General Ecuación Específica
Y=ax+b