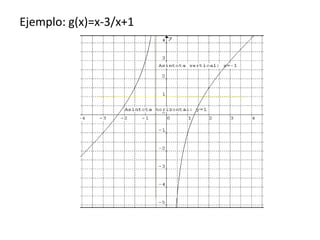
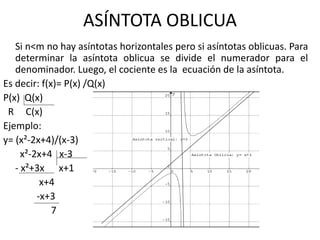
Este documento explica las características de las funciones racionales y cómo calcular e identificar las asíntotas verticales, horizontales y oblicuas. Las asíntotas son líneas que se acercan a la curva de una función racional sin cortarla. Se pueden calcular dividiendo los polinomios del numerador y denominador o encontrando los valores que anulan el denominador para las asíntotas verticales.

2. La función F, denotada por f(x)=P(x)/Q(x) donde P(x)
y Q(x) son polinomios y Q(x) ≠ 0 es la función general
racional, F= {(x,y) ЄRxR/y=P(x)/Q(x)}. Por ejemplo.
g(x)= x-3/x-1 f(x)= x+1/2x+4 h(x)= x²-4x/x-2
y=x² +4x+4/ y=x² -x-6 y= 1/x

3. GRÁFICAS DE FUNCIONES
RACIONALES
 La gráfica de una función de primer grado es siempre
una línea recta y la gráfica de una función de segundo
grado es una parábola. Estos enunciados no pueden
hacerse con respecto a una función racional.
 En la función racional se presentan asíntotas.
¿Qué es una asíntota?
Una asíntota es una recta que, prolongada
indefinidamente, se acerca de continuo a una curva sin
llegar nunca a encontrarla .
Existen tres tipos de asíntotas y todas podemos
calcularlas he identificarlas cuando se presenten.

4. Asíntota vertical.
Como su nombre lo indica, son rectas verticales
asociadas a la función. Se encuentran presentes
únicamente en funciones racionales de la forma
f(x)= P(x)/Q(x).
Para determinar la asíntota vertical se hallan las raíces
del denominador igualándolo a cero.
Por ejemplo: si g(x)= x-3/x+1 se tiene: x+1=0. Luego x=-1
es asíntota vertical.

5. ASÍNTOTA HORIZONTAL
Como su nombre lo indica son rectas horizontales asociadas
a la función. Se encuentran presentes únicamente en
funciones racionales de la forma f(x)= P(x)/Q(x).
La función P denotada por p(x) = + +…+ x+
donde , ,…, son constantes reales y m es un entero positivo
es la función polinomial de grado m, P= {(x,y) Є RxR /y = +
+…+ x+ }
La función Q, denotada por q(x)= + +…+ x+
donde , ,…, son constantes reales y n es un entero positivo
es la función polinomial de grado n, Q= {(x,y) Є RxR / y = +
+…+ x+ }
Luego sustituyendo las expresiones en la función general de la
función racional, se tiene:
f(x)= P(x)/Q(x), donde P(x) y Q(x) son polinomios y Q(x)
f(x)= +…+ x+ / +…+ x+ ; Q(x)

6. Para determinar la asíntota horizontal tomamos en cuenta
los grados de los polinomios y luego consideramos los
siguientes casos:
1.- El polinomio P(x) y Q(x)tiene el mismo grado, la asíntota esta dada
por el cociente de los coeficientes de grado mayor. Es decir : m=n la
recta y = am/bn, es una asíntota horizontal.
Por ejemplo: si g(x)= x-3/x+1 se tiene: y=1/1 =1.
2.- El grado del polinomio Q(x) es mayor que el de P(x). La asíntota es
la recta y=0. Es decir n>m la recta y=0 es una asíntota horizontal.
Por ejemplo: si f(x) = 4x+1/x²-5x+6 se tiene que y=0 es asíntota
horizontal.
3.- El grado del polinomio Q(x) es menor que el de P(x).
Para n<m, no hay asíntotas horizontales, pero hay asíntotas oblicuas.

7. Ejemplo: g(x)=x-3/x+1

8. ASÍNTOTA OBLICUA
Si n<m no hay asíntotas horizontales pero si asíntotas oblicuas. Para
determinar la asíntota oblicua se divide el numerador para el
denominador. Luego, el cociente es la ecuación de la asíntota.
Es decir: f(x)= P(x) /Q(x)
P(x) Q(x)
R C(x)
Ejemplo:
y= (x²-2x+4)/(x-3)
x²-2x+4 x-3
- x²+3x x+1
x+4
-x+3
7

9. OBSERVACIONES: (FUNCIÓN RACIONAL)
Asíntota vertical: 1. Una función puede tener infinitas asíntotas
verticales.
2. Las asíntotas verticales se hallan en los valores de x que anulan al
denominador.
3. La gráfica de la función no puede cortar a las asíntotas verticales.
Asíntota Horizontal: 1. Una función tiene como máximo dos asíntotas
horizontales.
2 La gráfica de la función no puede cortar a las asíntotas horizontales.
3.- Generalmente, si el grado del numerador es dos veces más
unidades mayor que el del denominador hay asíntota horizontal.
Asíntota Oblicua: 1. Una función puede tener como máximo dos
asíntotas oblicuas.
2.- Si una función tiene asíntota oblicua no tiene asíntota horizontal.
3.- La gráfica de la función puede cortar a las asíntotas oblicuas en
uno o varios puntos.