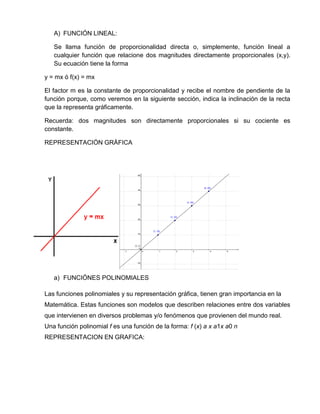
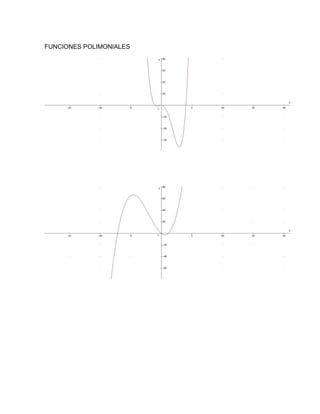
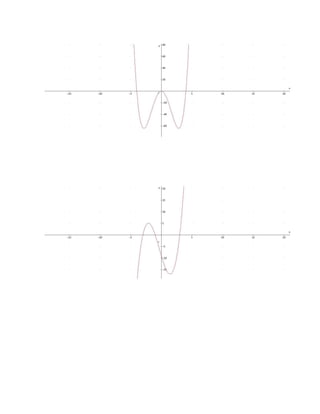
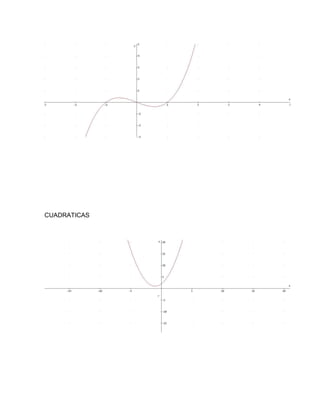
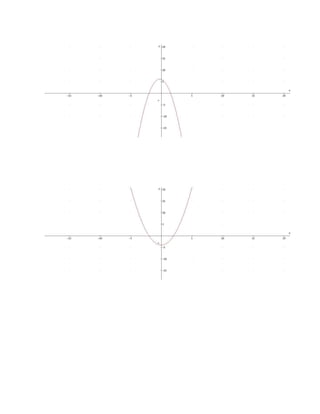
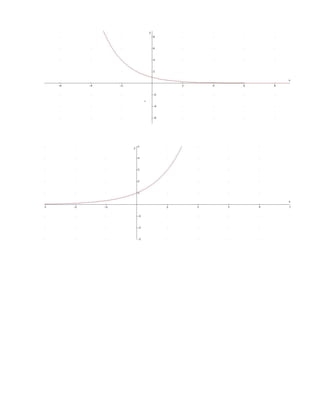
Este documento explica diferentes tipos de funciones y cómo graficarlas. Define funciones como relaciones entre variables donde cada valor de la variable independiente corresponde a un único valor de la variable dependiente. Explora funciones lineales, polinomiales, cuadráticas, racionales, exponenciales y logarítmicas, describiendo sus ecuaciones y representaciones gráficas. El autor concluye que aprendió sobre las gráficas de funciones, las cuales son útiles para resolver problemas de la vida cotidiana.

1. MATEMATICAS
LIC. JOSE ANTONIO FERRA CUEVAS
ALUMNA: INDRA ANUBIS RUIZ LOPEZ
LIC. TECNOLOGÍA EDUCATIVA
PRIMER CUATRIMESTRE
H. JUCHITAN DE ZARAGOZA OAXACA. A 10/12/14

2. INTRODUCCION
Este trabajo da a entender las diferentes funciones y las diferentes maneras de graficar, ya que son funciones esénciales para el graficado, ya que hace que aprendemos a graficar correctamente y dar el resultado correcto, espero y este bien y sea de su agrado.

3. FUNCIONES Y GRAFICAS
CONCEPTO DE FUNCIÓN
Una función es una relación establecida entre dos variables que asocia a cada valor de la primera variable (variable independiente x), un único valor de la segunda variable (variable dependiente y). Esta relación se representa mediante y = f(x). Una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman e irecorrido, también llamado rango o ámbito). Se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero): ... −2 → +4, −1 → +1, ±0 → ±0, +1 → +1, +2 → +4, +3 → +9, ...
GRÁFICA:
Para representar gráficamente una función y = f (x), es común utilizar un sistema de coordenadas rectangulares o cartesianas, en las cuales, la variable independiente x se representa
en el eje horizontal, y la variable dependiente y en el eje vertical.
TIPOS DE FUNCIONES
a) Función lineal
b) Función polinomial
c) Función cuadrática
d) Función racional
e) Función exponencial
f) Función logarítmicas

4. A) FUNCIÓN LINEAL:
Se llama función de proporcionalidad directa o, simplemente, función lineal a cualquier función que relacione dos magnitudes directamente proporcionales (x,y). Su ecuación tiene la forma
y = mx ó f(x) = mx
El factor m es la constante de proporcionalidad y recibe el nombre de pendiente de la función porque, como veremos en la siguiente sección, indica la inclinación de la recta que la representa gráficamente.
Recuerda: dos magnitudes son directamente proporcionales si su cociente es constante.
REPRESENTACIÓN GRÁFICA
a) FUNCIÓNES POLINOMIALES
Las funciones polinomiales y su representación gráfica, tienen gran importancia en la
Matemática. Estas funciones son modelos que describen relaciones entre dos variables que intervienen en diversos problemas y/o fenómenos que provienen del mundo real.
Una función polinomial f es una función de la forma: f (x) a x a1x a0 n
REPRESENTACION EN GRAFICA:

5. b) FUNCIÓN CUADRÁTICA
Una función cuadrática es aquella que tiene la forma, o puede ser llevada a la forma:
y = f (x) = ax2 + bx + c , con a ≠ 0 , a,b,c∈ IR
PRESENCION GRAFICA

6. c) FUNCIONES RACIONALES
Una función racional f es una función definida por una expresión algebraica que es el cociente de dos polinomios:
F= ( ) ( )
Donde p(x) y q(x) son polinomios, tal que q(x) ≠ 0.
d) FUNCIÓN EXPONENCIAL
Una función exponencial con base b es una función de la forma f(x) = bx , donde b y x son números reales tal que b > 0 y b es diferente de uno.
El dominio es el conjunto de todos los números reales y el recorrido es el conjunto de todos los números reales positivos.
1) f(x) = 2x

7. e) FUNNCIONES LOGARITMICAS
Las inversas de las funciones exponenciales se llaman funciones logarítmicas. Como la notación se utiliza para denotar una función inversa, entonces se utiliza otra notación para este tipo de inversas. Si f(x) = bx, en lugar de usar la notación (x), se escribe logb (x) para la inversa de la función con base b. Leemos la notación logb(x) como el “logaritmo de x con base b”, y llamamos a la expresión logb(x) un logaritmo.

8. CONCLUSION
Este trabajo fue un poco complicado, pero aprendí mucho ya que sé que a la larga me servirá mucho, las gráficas son muy importantes para lo que realizamos y para dar resultados al resolverlas, es de mucho valor y utilidad para resolver los problemas de la vida cotidiana.

9. FUNCIONES LINEALES

11. FUNCIONES POLIMONIALES

14. CUADRATICAS

17. FUNCIONES RACIONALES

19. FUNCION ESXPONENCIAL: