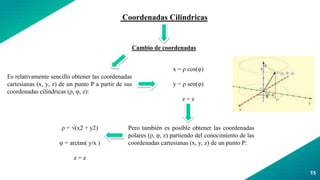
Este documento explica los diferentes sistemas de coordenadas como cartesianas, cilíndricas y esféricas. También describe las funciones de varias variables y cómo se definen el dominio y rango. Finalmente, introduce la transformación entre sistemas de coordenadas y conceptos como la simetría.