El documento describe los sistemas de coordenadas cartesianas y polares. Las coordenadas cartesianas se definen por dos ejes perpendiculares que se cortan en el origen, mientras que las coordenadas polares se definen por una distancia (r) desde el origen y un ángulo (α). El documento explica cómo convertir entre los dos sistemas usando trigonometría y el teorema de Pitágoras. También menciona otros sistemas de coordenadas como las coordenadas cilíndricas y esféricas.

1. Coordenadas polares
De Wikipedia
Las coordenadas polares son un sistema de coordenadas para definir la posición de un
punto en un espacio bidimensional consistente en un ángulo y una distancia.
En muchos casos, es útil utilizar las coordenadas cartesianas para definir una función en
el plano o en el espacio. Aunque en muchos otros, definir ciertas funciones en dichas
coordenadas puede resultar muy tedioso y complicado. En dichos casos, hacer uso de las
coordenadas polares o esféricas puede simplificarnos mucho la vida.
Definamos un sistema ortonormal con eje de abscisas X y eje de ordenadas Y. Tracemos
un vector centrado en el origen y acostado en el eje de las abscisas, y de longitud r. Si
ahora decidimos inclinarlo con un ángulo α, tendremos un vector definido por las
variables r y α. Es decir, para definir un punto en el plano por ejemplo podemos, bien
definir un par ordenado (x, y) en coordenadas cartesianas, bien dar un largo r de vector y
un ángulo α en coordenadas polares. Ambas precisan un mismo punto en el plano.
(Si trabajamos en el espacio, tenemos (x, y, z) como variables en las coordenadas
cartesianas, y (r,α,z) en coordenadas polares)
Como pasar de un sistema de coordenadas a otro
Utilizando las propiedades de la trigonometría clásica, tenemos que
;
de ahí obtenemos que ;
En este caso pasamos de las coordenadas cartesianas a polares.
Para pasar de polares a cartesianas, emplearemos el teorema de Pitágoras
(la suma de los cuadrados de los catetos es igual al cuadrado de la
hipotenusa), entonces:
;
Para calcular , basta calcular el arco seno de , de donde obtendremos dos valores
de , lo mismo para el arco coseno de , con otros dos valores. Con cualquiera de
estas tres ecuaciones obtenemos el ángulo buscado.
1

2. Sistema de coordenadas
Un sistema de coordenadas es un conjunto de valores que permiten definir
inequívocamente la posición de cualquier punto de un espacio geométrico respecto de
un punto denominado origen. El conjunto de ejes, puntos o planos que confluyen en el
origen y a partir de los cuales se calculan las coordenadas constituyen lo que se
denomina sistema de referencia.
Tabla de contenidos
• 1 Sistemas usuales
o 1.1 Sistema de coordenadas cartesianas
o 1.2 Sistema de coordenadas polares
o 1.3 Sistema de coordenadas cilíndricas
o 1.4 Sistema de coordenadas esféricas
o 1.5 Coordenadas geográficas
• 2 Véase también
• 3 Enlaces externos
Sistemas usuales
Sistema de coordenadas cartesianas
El sistema de coordenadas cartesianas es aquel que formado por dos ejes en el plano,
tres en el espacio, mutuamente perpendiculares que se cortan en el origen. En el plano,
las coordenadas cartesianas o rectangulares x e y se denominan respectivamente abscisa
y ordenada.
Sistema de coordenadas polares
Las coordenadas polares se definen por un eje que pasa por el origen (llamado eje
polar). La primera coordenada es la distancia entre el origen y el punto considerado,
mientras que la segunda es el ángulo que forman el eje polar y la recta que pasa por
ambos puntos.
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas es una generalización del sistema de coordenadas
polares plano, al que se añade un tercer eje de referencia perpendicular a los otros dos.
La primera coordenada es la distancia existente entre el origen y el punto, la segunda es
el ángulo que forman el eje y la recta que pasa por ambos puntos, mientras que la tercera
es la coordenada que determina la altura del cilindro.
Sistema de coordenadas esféricas
El sistema de coordenadas esféricas está formado por tres ejes mutuamente
perpendiculares que se cortan en el origen. La primera coordenada es la distancia entre
2

3. el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar
la posición del punto.
Coordenadas geográficas
Hay varios tipos de coordenadas geográficas. El sistema más clásico y conocido es el
que emplea la latitud y la longitud, que pueden mostrase en los siguientes formatos:
• DD Decimal Degree (Grados Decimales): ej. 49.500-123.500
• DM Degree:Minute (Grados:Minutos): ej. 49:30.0-123:30.0
• DMS Degree:Minute:Second (Grados:Minutos:Segundos): ej. 49:30:00-123:30:00
Otro sistema de coordenadas geográficas habitual es el sistema de coordenadas UTM.
Véase también
• Coordenadas celestes
• Tabla en coordenadas cilíndricas y esféricas
3

4. Coordenadas cartesianasDe Wikipedia
Las coordenadas cartesianas son un sistema de coordenadas formado por dos ejes en
el plano, tres en el espacio, mutuamente perpendiculares que se cortan en el origen. En
el plano, las coordenadas cartesianas o rectangulares x e y se denominan
respectivamente abscisa y ordenada.
En adelante, las magnitudes vectoriales en negrita.
Tabla de contenidos
• 1 Sistema de coordenadas plano
• 2 Sistema de coordenadas espacial
• 3 Cambio del sistema de coordenadas
o 3.1 Traslación del origen
 3.1.1 Traslación del origen (en valores absolutos)
 3.1.2 Traslación del origen (en valores relativos)
o 3.2 Rotación alrededor del origen
• 4 Temas relacionados
• 5 Véase también
Sistema de coordenadas plano
Sistema de coordenadas cartesianas
Las ecuaciones de los ejes x e y son respectivamente y=0 y x=0, rectas que se cortan en
el origen 0 cuyas coordenadas son, obviamente, (0,0). Se denomina también abscisa al
eje x y ordenada al eje y. Los ejes dividen el espacio en cuatro cuadrantes en los que los
signos de las coordenadas alternan de positivo a negativo; así por ejemplo las
4

5. coordenadas del punto A serán ambas positivas, mientras que las del punto B serán
ambas negativas.
Las coordenadas de un punto cualquiera vendrán dadas por las proyecciones del
segmento entre el origen y el punto sobre cada uno de los ejes.
Sobre cada uno de los ejes se definen vectores unitarios (i y j) como aquellos paralelos
a los ejes y de módulo (longitud) la unidad. En forma vectorial, la posición del punto A
se define respecto del origen con las componentes del vector OA.
La posición del punto A sera:
Nótese que la lista de coordenadas puede expresar tanto la posición de un punto como
las componentes de un vector en notación matricial.
La distancia entre dos puntos cualesquiera vendrá dada por la expresión:
aplicación del teorema de Pitágoras al triángulo rectángulo ABC.
Un vector cualquiera AB se definirá restando, coordenada a coordenada, las del punto
de origen de las del punto de destino:
Evidentemente, el módulo del vector AB será la distancia dAB entre los puntos A y B
antes calculada.
Sistema de coordenadas espacial
coordenadas cartesianas espaciales
Los planos de referencia XY (z = 0); XZ (y = 0); e YZ (x = 0) dividen el espacio en 8
octantes en los que como en el caso anterior los signos de las componentes cambian de
positivo a negativo; téngase en cuenta que con los cuatro casos del plano, ahora caben
dos posibilidades z < 0 y z > 0.
5

6. La generalización de las relaciones anteriores al caso espacial es inmediata
considerando que ahora es necesaria una tercera coordenada (z) para definir la posición
del punto.
Las coordenadas del punto A seran:
La distancia entre los puntos A y B sera:
El segmento AB sera:
Cambio del sistema de coordenadas
Tanto en el caso plano como en el caso espacial pueden considerarse dos
transformaciones elementales: Traslación (del origen) y Rotación (alrededor de un eje).
Traslación del origen
Pueden considerarse 2 traslaciones:
1. Según el aspecto absoluto: Al pasar a otra posición, se indican las coordenadas
de dicha posición.
2. Según el aspecto relativo: Al pasar a otra posición, se indican las coordenadas a
partir de la actual.
Traslación del origen (en valores absolutos)
Traslación del origen en coordenadas cartesianas
Suponiendo que en el sistema de coordenadas inicial con origen en O las coordenadas
de un punto como el A sean (xb, yA), y que el origen se traslade a O' (xO, yO); las
coordenadas del punto A, respecto del sistema trasladado serán:
6

7. OA = OO' + O'A
despejando
O'A = OA - OO' = (xA, yA) - (xO, yO) = (xA - xO, yA - yO)
por tanto
x'A = xA - xO
y'A = yA - yO
z'A = zA - zO (en el caso espacial)
Traslación del origen (en valores relativos)
Traslación Relativa
Cuando lo que se ofrece no es una coordenada final, sino un dato de traslación respecto
de A ,puede considerarse la traslación (A1
), como la suma de coordenadas de A + el
desplazamiento. (Hay que notar que un desplazamiento, relativo, implica que A es el
centro de coordenadas relativas sobre D)
Es decir: Sea el desplazamiento D (Dx, Dy), entonces;
Si A=(xA, yA) entonces A + D = (xA, yA)+(Dx, Dy);
Finalmente, agrupando:
A1
=(xA + Dx), (yA + Dy) y para el caso espacial: ,(zA + Dz)
Rotación alrededor del origen
7

8. Rotación alrededor del origen en coordenadas cartesianas
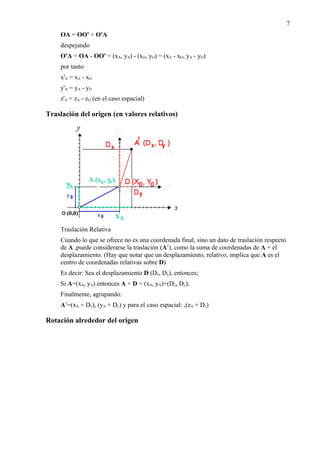
Supongamos ahora, que el nuevo sistema de coordenadas, ejes x' e y', resulta del giro
del primitivo (x, y) un cierto ángulo α alrededor del origen de coordenadas.
Dado que los triángulos rectángulos sombreados son semejantes, a partir de las
relaciones trigronométricas entre sus lados, fácilmente podemos obtener las nuevas
coordenadas:
Del triángulo Ox'A1; x'A = 01 · cos α = (xA + xA1) · cos α
Del triángulo AxA1; xA1 = yA · tg α
Sustituyendo en la primera ecuación:
x'A = (xA + yA · tg α) · cos α = xA · cos α + yA · sen α
Operando de formabola de putoscon los triángulos 0y'A2 y AyA2, obtendríamos, como
fácilmente se puede demostrar:
y'A = - xA · sen α + yA · cos α
Expresando matricialmente el cambio de coordenadas:
{OA'} = [T] {OA}
Siendo [T] la matriz de transformación y cuyas filas son precisamente las
componentes de los vectores unitarios i ' y j ' respecto de los originales i y j, o si se
prefiere, cuyas columnas son las componentes de los vectores unitarios originales en el
sistema de referencia rotado.
Temas relacionados
• Espacio vectorial
8

9. • Combinación lineal
• Sistema generador
• Independencia lineal
• Base (álgebra)
• Base Ortogonal
• Base Ortonormal
• Producto escalar
• Producto vectorial
• Producto mixto
• Producto tensorial
9

10. •
Función matemática
)
En matemáticas se denomina función a la correspondencia o relación de cada elemento
de un conjunto A con un único elemento del conjunto B. Se simboliza con
si y sólo si cumple con las siguientes condiciones:
1. Existencia:
2. Unicidad: Si
Esto significa que a cada elemento x de A, le corresponde por f un y sólo un elemento y
de B. Que suele escribirse:
Se le adjudica a Leibniz (1646-1716) el haber utilizado por primera vez la palabra
función (del latín functo, "acto de realizar"). La definición formal se le atribuye a
Dirichlet (1805-1859).
Tabla de contenidos
• 1 Dominio e imagen
• 2 Tipos de funciones
o 2.1 Composición de funciones
o 2.2 Funciones reales y funciones discretas
o 2.3 Funciones acotadas
o 2.4 Paridad e imparidad de funciones
o 2.5 Funciones monótonas
Conceptos en el
Cálculo
Teorema fundamental |
Función | Límite |
Continuidad | Teorema
del valor medio |
Cálculo vectorial |
Cálculo tensorial
Derivación
Regla del producto |
Regla del cociente |
Regla de la cadena |
Función implícita |
Teorema de Taylor
Integración
Métodos de integración |
Integrales impropias |
Lista de integrales
10

11. o 2.6 Funciones periódicas
o 2.7 Funciones convexas
o 2.8 Funciones cóncava
• 3 Véase también
Dominio e imagen
• El dominio de una función es el conjunto de existencia de la misma, o sea los valores
para los cuales la función está definida. Entonces, el dominio de una función f es el
conjunto de todos los valores que puede tomar la variable independiente. Se denota
Dom f o Df.
• El conjunto imagen, también llamado codominio, está formado por los valores que
alcanza la función. Entonces, la imagen de una función f es el conjunto de todos los
valores que toma la variable dependiente. Se denota Im f o If.
Es decir que la función f(x) = x + 1 tiene como dominio e imagen todos los números
reales, pero una función g(x) = x², si bien tendrá como dominio a todos los reales, sólo
tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un
número real.
• Siempre es posible restringir tanto el conjunto dominio e imagen de una función con
un propósito determinado. Por ejemplo, si se quiere restringir f(x) = x² para que sea
biyectiva, es posible tomar una sóla de las ramas de modo que el dominio restringido y
el conjunto imagen tomen valores del intervalo [0,+∞].
• Conjunto de ceros: Es el conjunto de puntos pertenecientes al dominio de la función
para los cuales dicha función vale cero.
• Conjunto de negatividad: Es el conjunto de puntos pertenecientes al dominio de la
función para los cuales dicha función toma valores negativos.
• Conjunto de positividad: Es el conjunto de puntos pertenecientes al dominio de la
función para los cuales dicha función toma valores positivos.
Tipos de funciones
• Función inyectiva: Si cada elemento de la imagen es imagen de como máximo un
único elemento del dominio. es inyectiva
; o lo que es lo mismo:
11

12. • Función sobreyectiva: es sobreyectiva si el conjunto imagen coincide
con el conjunto B (denominado también conjunto de llegada, codominio o rango).
es sobreyectiva
• Función biyectiva: es biyectiva si es inyectiva y sobreyectiva.
• Función inversa: Sólo si una función es biyectiva es posible hallar su
inversa
Sobreyectiva, no inyectiva Inyectiva, no sobreyectiva
Biyectiva No sobreyectiva, no inyectiva
Véase también:: Lista de funciones matemáticas.
Composición de funciones
• Dadas dos funciones f y g para las cuales la imagen de g está incluida en el dominio de
f entonces se puede construir su composición:
• Dada biyectiva, existe tal que
para toda y para toda . Véase función recíproca.
Funciones reales y funciones discretas
12

13. • Si el dominio de una función es un intervalo de la recta real la función se denominará
real. En cambio, si la función está definida para los números enteros se denominará
función discreta. Un ejemplo de una función discreta son las sucesiones.
Funciones acotadas
• Una función se denomina acotada si su conjunto imagen está acotado. Ejemplo: f(x) =
sen(x) y g(x) = cos(x) cuyo conjunto imagen es [-1,1]
Paridad e imparidad de funciones
• Una función puede ser par, impar o ninguna de las dos.
1. Función par:
2. Función impar:
Funciones monótonas
1. f es estrictamente creciente en
2. f es estrictamente decreciente en
Si una función es estrictamente creciente o decreciente entonces es biyectiva.
1. f es creciente en
2. f es decreciente en
Funciones periódicas
Una función es periódica si se cumple: donde es el período.
En particular, una función es periódica alternada cuando se cumple:
. Estas últimas también son conocidas como funciones
simétricas de media onda y constan de dos semiondas iguales de sentidos opuestos
] Funciones convexas
Función convexa.
13

14. Una función es convexa en un intervalo si la rectas tangentes a la función es ese
intervalo están por debajo de la función.
Funciones cóncava
Una función es cóncava en un intervalo si la rectas tangentes a la función es ese
intervalo están por encima de la función.
Wikimedia
Commons
alberga
funciones
Vector
El término vector puede referirse a:
• En física, un vector hace referencia a una magnitud en la que importan el valor, el
punto de aplicación, la dirección y el sentido.
• En matemática, un vector es un elemento de un campo vectorial o de un espacio
vectorial.
• En geometría, segmento orientado.
• En informática, un vector es un conjunto de variables o registros del mismo tipo.
• En epidemiología y ecología se llama vector a un mecanismo portador de un agente
infeccioso. Como podría ser el mosquito Anopheles que transporta el Plasmodium,
causante de la malaria.
• En genética y biotecnología, un vector es un agente, que puede ser un virus o un
pequeño fragmento de ADN llamado plásmido, que porta un gen extraño o modificado.
Cuando se usa en terapia génica, el vector pasa el gen deseado a una célula objetivo.
Ésta es una página de desambiguación, una ayuda a la navegación que enumera otras
páginas que de otra forma compartirían el mismo título. Si llegaste aquí a través de un
enlace interno, regresa por favor para corregirlo de modo que apunte al artículo
apropiado.
14

15. Trigonometría
La trigonometría (del griego, la medición de los triángulos) es una rama de las
matemáticas que estudia los ángulos, triángulos y las relaciones entre ellos (funciones
trigonométricas).
Posee muchas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en
astronomía para medir distancias a estrellas próximas, en geografía para medir
distancias entre puntos geográficos, y en sistemas de navegación por satélites.
Tabla de contenidos
• 1 Unidades angulares
• 2 Funciones seno y coseno
• 3 Función tangente
• 4 Fórmulas trigonométricas elementales
• 5 Véase también
Unidades angulares
Las unidades de medida de ángulos más conocidas son los grados, minutos y segundos.
Este tipo de medidas está basada en la división en partes iguales de una circunferencia.
Las equivalencias son las siguientes:
360° = un giro completo alrededor de una circunferencia
180° = 1/2 vuelta alrededor de una circunferencia
90° = 1/4 de vuelta
1° = 1/360 de vuelta, etc.
También se puede definir otra unidad angular, el radián, que en las aplicaciones físicas
es mucho más práctico y directo que trabajar con grados.
La magnitud de un ángulo medido en radianes está dada por la longitud del arco de
circunferencia que se obtiene, dividido por el valor del radio. El valor de este ángulo es
independiente del valor del radio.
De esta forma, se puede calcular fácilmente la longitud de un arco de circunferencia;
solo basta multiplicar el radio por el ángulo en radianes.
Long. arco de circunferencia = [Ángulo en radianes] × [Radio de la circunferencia]
Ya que conocemos el perímetro de una circunferencia de radio, r, unitario:
entonces el ángulo de una circunferencia completa, medido en radianes es 2 × π. Como
además sabemos que este mismo ángulo, medido en grados mide 360°, entonces
podemos definir una equivalencia:
2 × π radianes = 360°
y por tanto:
15

16. 1 radián = 360°/(2 × π) = 57,29°
a partir de esta igualdad, determinamos que: 90° = π/2 radianes 60° = π/3 radianes 45° =
π/4 radianes 30° = π/6 radianes
Funciones seno y coseno
El triángulo ABC es un triángulo rectángulo y lo usaremos para definir las funciones
seno y coseno.
En un triángulo rectángulo, el seno (abreviado como sen o sin) es la razón entre el cateto
opuesto y la hipotenusa, y el coseno (abreviado como cos) es la razón entre el cateto
adyacente y la hipotenusa.
Si usamos una circunferencia unitaria (con radio igual a uno), entonces la hipotenusa,
AB, del triángulo se hace 1, por lo que las relaciones quedan:
sen α = cos β = |BC| / |AB| = |BC| / 1 = |BC| = a
cos α = sen β = |AC| / |AB| = |AC| / 1 = |AC| = b
A continuación algunos valores de las funciones que es conveniente recordar:
áng
ulo
sen cos tg ctg sec csc
00
0 1
300
2
450
1 1
16

17. 600
2
900
0 1
Como en el triángulo rectángulo se cumple que a2
+ b2
= c2
, de la figura anterior se tiene
que sen α = a, cos α = b, c = 1; entonces para todo ángulo α:
sin2
(α) + cos2
(α) = 1
Algunas identidades trigonométricas importantes son las siguentes:
sen (90 - α) = cos α
cos (90 - α) = sen α
sen (180 - α) = sen α
cos (180 - α) = -cos α
sen 2α = 2 sen α cos α
cos 2α = cos2
α - sen2
α
sen (α + β) = sen α cos β + cos α sen β
cos (α + β) = cos α cos β - sen α sen β
sen (α - β) = sen α cos β - cos α sen β
cos (α - β) = cos α cos β + sen α sen β
sen²(α) = 1/2 * (1 - cos(2 * α);
cos²(α) = 1/2 * (1 + cos(2 * α);
Véase también:
Sinusoide
Función tangente
En un triángulo rectángulo, la tangente (abreviada como tan o tg) es la razón entre el
cateto opuesto y el cateto adyacente.
tan(a) = BC / AC = sin(a) / cos(a)
El valor de la tangente para algunos ángulos importantes es:
tan = AC / OA = BD / OB = sen / cos
tan (π/2) = tan (90°) = +∞
tan (-π/2) = tan (-90°) = -∞
tan (0) = 0
tan (π/4) = tan (45°) = 1
tan (π/3) = tan (60°)=
17

18. tan (π/6) = tan (30°) =
Una ídentidad de importancia con la tangente es:
Fórmulas trigonométricas elementales
Estas son las seis funciones trigonométricas básicas:
•
•
•
•
•
•
David P. LHEMI
Véase también
• Identidad trigonométrica
• Funciones hiperbólicas
• Lista de integrales de funciones trigonométricas
18

19. Teorema de Pitágoras
El Teorema de Pitágoras establece que en un triángulo rectángulo la suma de los
cuadrados de los catetos es igual al cuadrado de la hipotenusa:
Este teorema fue propuesto por Pitágoras de Samos (582 adC - 496 adC), un filósofo y
matemático griego.
Tabla de contenidos
•
• 1 Demostración
• 2 Corolario del Teorema de Pitágoras
• 3 El teorema de pitágoras en el espacio
o 3.1 Demostración
• 4 Véase también
Demostración
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el
área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y
lado b.
19

20. Si añadimos tres iguales al original alrededor del cuadrado de lado c formando la figura
mostrada en la imagen, obtenemos un cuadrado. En efecto, si la figura central de lado c
primeramente dibujada es un cuadrado, sus lados formarán ángulos rectos, entonces, si
giramos el triángulo original 90º alrededor del centro del cuadrado, vendrá a ocupar una
posición perpendicular a la original, de modo tal que el lado a será colineal al lado b y
viceversa, formándose un cuadrado de lado a + b.
El área de este cuadrado puede expresarse de dos maneras:
• El cuadrado del lado:
• Suma del cuadrado original y los triángulos añadidos:
Igualando ambas expresiones:
y simplificando:
Corolario del Teorema de Pitágoras
Números impares
Sea un número x impar, entonces los números correspondientes al trío pitagórico
asociados a este número son:
20

21. La demostración de las expresiones anteriores corresponde al desarrollo de la siguiente
igualdad:
Números pares
Sea un número y par, entonces los número correspondientes al trío pitagórico asociados
a este número son:
La demostración de las expresiones anteriores corresponde al desarrollo de la siguiente
igualdad:
El teorema de pitágoras en el espacio
El teorema de pitágoras se puede aplicar también en un espacio tridimensional.
21

22. Demostración
Para hallar la longitud de la diagonal D hallamos primero la longitud de la diagonal d:
Ahora tenemos un triángulo rectángulo de catetos b y d, e hipotenusa D. Ahora
utilizamos el teorema de pitágoras de nuevo para hallar la longitud de la hipotenusa.
El exponente 2 elimina la raíz cuadrada, quedando:
Véase también
Wikimedia
Commons
alberga
contenido
multimedia
sobre
Teorema de
Pitágoras
22

23. Categoría:Geometría
Subcategorías
Se listan 14 subcategorías de esta categoría.
A
• Ángulos
C
• Curvas
F
• Fractales
G
• Geometría
algebraica
G cont.
• Geometría analítica
• Geometría de
Riemann
• Geometría del espacio
• Geometría descriptiva
• Geometría diferencial
G cont.
• Geometría euclidiana
• Geometría
tetradimensional
P
• Poliedros
• Politopos
T
• Trigonometría
Artículos en la categoría «Geometría»
Se listan 122 artículos de esta categoría.
• Geometría
1
• 1-variedad
3
• 3-variedad
4
• 4-variedad
A
• Abatimiento
• Alto dimensional
• Altura de un triángulo
• Ancho
• Ángulo
• Apotema
• Asíntota
B
• Baricentro
• Bidimensional
F
• Figura
• Flexágono
• Función circular
• Fórmula de Euler
• Fórmula de Herón
G
• Geodésica
• Geometría algebraica
• Geometría analítica
• Geometría del espacio
• Geometría descriptiva
• Geometría euclídea
• Geometría hiperbólica
• Geometría plana
• Geometría proyectiva
• Geometrías no
euclídeas
• Grado centesimal
P cont.
• Poliedro
• Posición
• Postulados
característicos
• Postulados de Euclides
• Primitiva geométrica
• Producto escalar
• Programa de Erlangen
• Proyección
• Punto (geometría)
• Punto medio
• Puntos cocíclicos
• Puntos de Euler
Q
• Quinto postulado de
Euclides
R
• Recta
23

24. • Bisectriz
C
• Característica de Euler
• Categoría de Lusternik-
Schnirelmann
• Celda (matemáticas)
• Celda unitaria
• Centro (Geometría)
• Cilindro (geometría)
• Circuncentro
• Compás (geometría)
• Constructive Solid
Geometry
• Coordenadas cartesianas
• Coordenadas cilíndricas
• Coordenadas esféricas
• Coordenadas polares
• Corona (matemática)
• Cuadratura
(trigonometría)
• Curva
• Círculos exinscritos
D
• Deltoide
• Diagonal
• Diedro
• Distancia
• Distancia euclidiana
• Diámetro
E
• Eje de simetría
• Escuadra
• Espacio sobrio
• Grado sexagesimal
• Gran círculo
H
• Historia de la
Geometría
• Homotecia
• Hélice (geometría)
I
• Incentro
• Inclinación
• Isógona
L
• Lado (geometría)
• Longitud dimensional
• Lugar geométrico
• Línea
M
• Magnitud
(matemática)
• Media aritmética
geométrica
• Mediana (geometría)
• Mediatriz
O
• Orientación
(geometría)
• Ortocentro
P
• Pantógrafo
• Paralelismo
• Paralelogramo
• Particionado del
espacio
• Perpendicularidad
• Perímetro
• Plano proyectivo
• Recta de Euler
• Recta de Simson
• Red irregular de
triángulos
• Región angular
S
• Sector circular
• Segmento
• Semiplano
• Semirrecta
• Simetría
• Simplex
• Sistema de
coordenadas
• Superficie
• Superficie de
revolución
• Superfórmula
• Sólido de revolución
T
• Teorema de Desargues
• Teorema de Pappus
• Teorema de Pitágoras
• Teorema de Tales
• Teorema de la Función
Implícita
• Teorema del hexágono
de Pappus
• Traslación
• Tridimensional
V
• Variedad diferenciable
• Vector (geometría)
• Vértice
Y
• Y-homeomorfismo
24