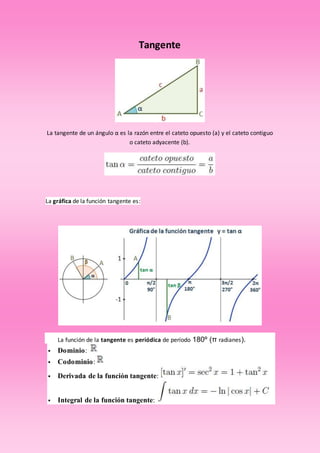
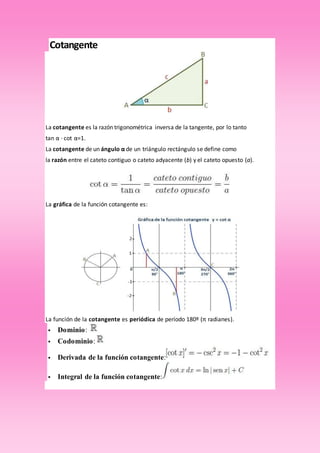
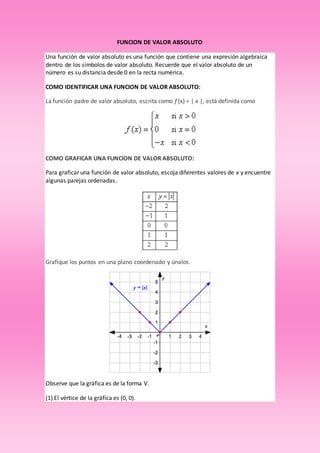
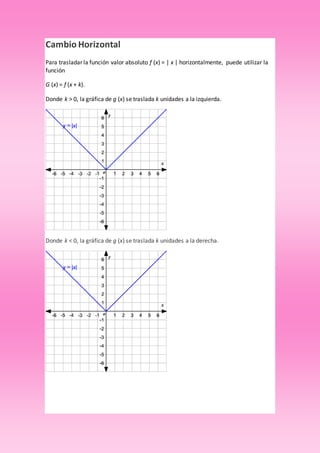
El documento describe diversas funciones matemáticas, incluyendo funciones racionales, trigonométricas, de valor absoluto, exponenciales y logarítmicas, y explica sus características, identificación y formas de graficarlas. Se enfatiza el comportamiento en el infinito, la continuidad y las asíntotas. También se discuten propiedades específicas de cada tipo de función, como dominio, codominio y periodicidad.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACION
INSTITUTO UNIVERSITARIO DE TECNOLOGIA ‘’ANTONIO JOSE DE SUCRE’’
EXTENSION BARCELONA – PUERTO LA CRUZ
FUNCIONES (TIPO ll)
Profesora: Ranielina Rondón Bachiller: Daniela Bittar
C.I 29.538.990

2. FUNCIONES RACIONALES
Una función racional es una función que puede escribirse como cociente de dos
polinomios.
Si el denominador es un número (un polinomio de grado 0), entonces la función es un
polinomio. Por lo tanto, las funciones polinómicas son funciones racionales. En estas
páginas sobre funciones racionales vamos a considerar solamente funciones racionales
cuyo denominador es un polinomio de grado mayor que 0.
COMO IDENTIFICAR UNA FUNCION RACIONAL:
Las funciones racionales pueden tener características que las diferencian de las
funciones polinómicas para identificarlas tenemos que tomar en cuenta lo siguiente:
- Singularidades: En algunos casos, algunos valores de x son problemáticos. Esto es
debido a que las funciones racionales hay un denominador que puede ser 0 y no
podemos dividir entre 0. Esos valores de x que hacen 0 el denominador juegan un
papel especial. Como no podemos calcular el valor de la función en esos valores
decimos que la función no está definida para esos valores de x.
- Puntos de corte con el eje de abscisas: Se trata de encontrar los valores de x que
hacen que el gráfico de la función cruce el eje de abscisas. Son los valores de x para los
que f(x)=0.
- Continuidad: Las funciones racionales son continuas en su dominio (pero su dominio
puede no ser todos los números reales).
- Comportamiento "en el infinito": Es interesante el estudio del comportamiento de la
función cuando x se hace más y más grande en valor absoluto (siendo x positivo o
negativo). Veremos que en algunos casos la función se aproxima a una recta
(horizontal u oblicua).

3. COMO GRAFICAR UNA FUNCION RACIONAL:
Empezamos nuestro estudio con las funciones racionales lineales. Una función racional
lineal es una función racional cuyo numerador es un número o un polinomio de grado
1 y que tiene por denominador un polinomio de grado 1.
La más simple de las funciones racionales es:
Al dibujar su gráfica obtenemos una hipérbola equilátera.
Cuando x=0 no podemos calcular el valor de la función porque no podemos dividir
entre 0 (abusando del lenguaje, a veces se dice que 'el cociente se hace infinito'). La
función no está definida en x=0. Es decir, el dominio de la función es:
DOM F= R – (0)

4. Para x = 1 resulta y = 1. Para x > 1 el numerador es más pequeño que el denominador y
el cociente resulta menor que 1.
Veamos con más detalle el comportamiento de la función cuando x se hace más y más
grande. Conforme aumenta x la fracción 1/x disminuye. Por lo tanto, si nos movemos
desde el 0 hacia la derecha, el valor de y=1/x es cada vez menor y la curva se aproxima
al eje de abscisas tanto como queramos. Es decir, la función se comporta como una
recta horizontal. A esta recta la llamamos asíntota horizontal.
La recta y=b es una asíntota horizontal de la gráfica de f(x) si f(x) se aproxima a b
conforme x aumenta o disminuye sin cota.
En este primer caso, la asíntota horizontal es el eje de abscisas:
Y=0

5. Cuando nos aproximamos a 0 por el lado del 1 (valores positivos), el denominador se
está aproximando a 0 mientras que el numerador es igual a 1. La función aumenta
cuanto queramos, aumenta sin límite y obtenemos una rama que se 'va hacia el
infinito'.
Si nos aproximamos a 0 por la izquierda (valores negativos) entonces la gráfica de la
función se 'va hacia el infinito' pero negativo.
Decimos que la función tiene una asíntota vertical. La gráfica de esta función está
dividida en dos 'ramas'.
La recta x=b es una asíntota vertical de la gráfica de f(x) si f(x) crece o decrece sin cota
conforme x se acerca a b por la derecha o por la izquierda.
Una función racional tendrá asíntotas verticales en los ceros del denominador (pero
tendremos que comprobar el comportamiento de la función en los casos en que un
cero del denominador también sea cero del numerador).

6. FUNCION TRIGONOMETRICA
Una función trigonométrica f es aquella que está asociada a una razón trigonométrica.
Éstas extienden su dominio a los números reales.
COMO IDENTIFICAR UNA FUNCION TRIGONOMETRICA:
Las razones trigonométricas de un ángulo α son las obtenidas entre los tres lados de
un triángulo rectángulo. Es decir, las comparaciones por su cociente de sus tres lados
a, b y c.
COMO GRAFICAR UNA FUNCION TRIGONOMETRICA:
Existen seis funciones trigonométricas:
Seno
El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la
hipotenusa (c).

7. La gráfica de la función seno es:
La función del seno es periódica de período 360º (2π radianes), por lo que esta sección
de la gráfica se repetirá en los diferentes períodos.
La función del coseno es periódica de período 360º (2π radianes).
 Dominio:
 Codominio:
 Derivada de la función coseno:
 Integral de la función coseno:

8. Tangente
La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo
o cateto adyacente (b).
La gráfica de la función tangente es:
La función de la tangente es periódica de período 180º (π radianes).
 Dominio:
 Codominio:
 Derivada de la función tangente:
 Integral de la función tangente:

9. Cosecante
La cosecante es la razón trigonométrica inversa del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón
entre la hipotenusa (c) y el cateto opuesto (a).
La gráfica de la función cosecante es:
La función de la cosecante es periódica de período 360º (2π radianes).
 Dominio:
 Codominio:
 Derivada de la función cosecante:
 Integral de la función cosecante:

10. Secante
La secante es la razón trigonométrica inversa del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de un triángulo rectángulo se define como la razón entre
la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).
La gráfica de la función secante es:
La función de la secante es periódica de período 360º (2π radianes).
 Dominio:
 Codominio:
 Derivada de la función secante:
 Integral de la función secante:

11. Cotangente
La cotangente es la razón trigonométrica inversa de la tangente, por lo tanto
tan α · cot α=1.
La cotangente de un ángulo α de un triángulo rectángulo se define como
la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).
La gráfica de la función cotangente es:
La función de la cotangente es periódica de período 180º (π radianes).
 Dominio:
 Codominio:
 Derivada de la función cotangente:
 Integral de la función cotangente:

12. FUNCION DE VALOR ABSOLUTO
Una función de valor absoluto es una función que contiene una expresión algebraica
dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un
número es su distancia desde 0 en la recta numérica.
COMO IDENTIFICAR UNA FUNCION DE VALOR ABSOLUTO:
La función padre de valor absoluto, escrita como f (x) = | x |, está definida como
COMO GRAFICAR UNA FUNCION DE VALOR ABSOLUTO:
Para graficar una función de valor absoluto, escoja diferentes valores de x y encuentre
algunas parejas ordenadas.
Grafique los puntos en una plano coordenado y únalos.
Observe que la gráfica es de la forma V.
(1) El vértice de la gráfica es (0, 0).

13. (2) El eje de simetría (x = 0 o eje de las Y) es la recta que divide la gráfica en dos
mitades congruentes.
(3) El dominio es el conjunto de todos los números reales.
4) El rango es el conjunto de todos los números reales mayores que o iguales a
0. .
(5) La intercepción en x y la intercepción en y ambas son 0.
Cambio Vertical
Para trasladar la función valor absoluto f ( x ) = | x | verticalmente, puede utilizar la
función
g ( x ) = f ( x ) + k .
Donde k > 0, la gráfica de g (x) se traslada k unidades hacia arriba.
Donde k < 0, la gráfica de g (x) se traslada k unidades hacia abajo.

14. Cambio Horizontal
Para trasladar la función valor absoluto f (x) = | x | horizontalmente, puede utilizar la
función
G (x) = f (x + k).
Donde k > 0, la gráfica de g (x) se traslada k unidades a la izquierda.
Donde k < 0, la gráfica de g (x) se traslada k unidades a la derecha.

15. FUNCION EXPONENCIAL
COMO IDENTIFICAR UNA FUNCION EXPONENCIAL:
1) El dominio de una función exponencial es R.
2) Su recorrido es (0, +∞)
3) Son funciones continuas.
4) Como a0 = 1, la función siempre pasa por el punto (0, 1).
La función corta el eje Y en el punto (0, 1) y no corta el eje X.
5) Como a1 = a, la función siempre pasa por el punto (1, a).
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son siempre concavas.
8) El eje X es una asíntota horizontal.
Si a > 1:
Al elevar un número mayor que 1 a cantidades negativas cada vez más grandes, el
valor de la potencia se acerca a cero, por tanto:
Cuando x → - ∞, entonces a x → 0
Si 0 < a < 1:
Ocurre lo contrario que en el caso anterior:
Cuando x → + ∞, entonces a x → 0
Las funciones exponenciales son las funciones que tienen la variable
independiente x en el exponente, es decir, son de la forma:

16. COMO GRAFICAR UNA FUNCION EXPONENCIAL:
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞)
3) Puntos de corte:
F(0) = 20 = 1, el punto de corte con el eje Y es (0, 1).
G(0) = - 20 = 1, el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1
La función g(x) es decreciente ya que 0 < a < 1
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son cóncavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asíntota en el eje X.

17. 7) Tabla de valores:

18. FUNCION LOGARITMICA
Una función logarítmica está formada por un logaritmo de base a, y es de la forma:
Siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.
La función logarítmica es la inversa de la función exponencial.
COMO IDENTIFICAR UNA FUNCION LOGARITMICA:
 Dominio:
El dominio son todos los números reales positivos.
 Recorrido:
El recorrido son todos los números reales.
 Derivada de la función logarítmica:
Las funciones logarítmicas son continuas.

19.  Si a es mayor que 1 (a > 1), la función es estrictamente creciente. En cambio,
si a es menor que 1 (a < 1), la función es estrictamente decreciente.
 La imagen de 1 siempre es 0 y la imagen de a es 1.
Así pues, las funciones logarítmicas siempre pasan por los puntos (1,0) y (a, 1).
La función logarítmica es inyectiva.

20. Todas las funciones logarítmicas cumplen las siguientes propiedades:
1. Función logarítmica del producto:
2. Función logarítmica de la división:
3. Función logarítmica del inverso multiplicativo:
4. Función logarítmica de la potencia:
COMO GRAFICAR UNA FUNCION LOGARITMICA:
Logaritmos
Sean dos números reales a y b, siendo a ≠ 1. El logaritmo en base a de b es el
elemento al que hay que elevar el número a para dé como resultado el número b.
Por ejemplo, el logaritmo en base 3 de 9 es 2, ya que siendo a = 3 y b = 9, el número al
que hay que elevar 3 para que dé 9 es 2, 32 = 9.
Cuando el logaritmo es en base 10 (a = 10), se llama logaritmo decimal y no se suele
escribir la base: f(x) = log x. También se llaman algoritmos comunes.

21. Normalmente, cuando no se especifica la base, se entiende como función logarítmica
la que tiene de base el número e(a = e = 2,7182818…). En este caso se
llama logaritmo neperiano (o logaritmo natural) y suele escribirse: f(x) = ln x.
Ejemplo
Supongamos que tenemos la función logarítmica con a = 2, definida por
la función:
La función es continua en todos los números reales positivos.
Como a = 2 > 1, la función es creciente.
Como podemos ver en su gráfica, la función pasa por los puntos (1, 0) y (2, 1).