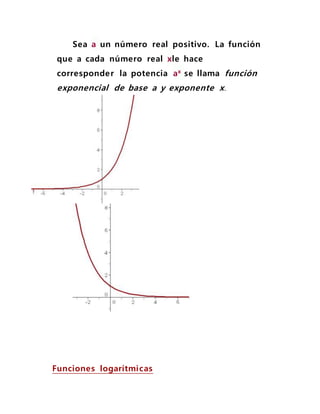
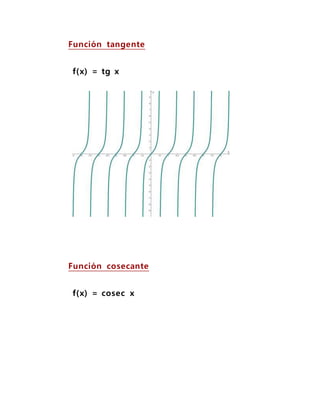
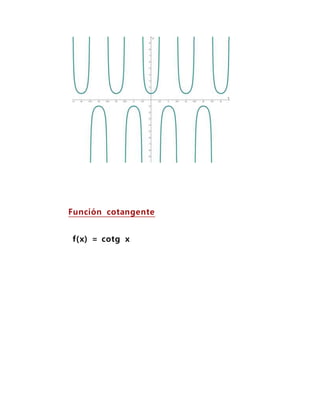
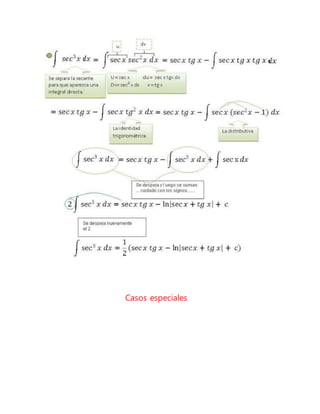
Este documento describe las funciones trascendentales, que son funciones que no pueden expresarse en términos de operaciones algebraicas. Explica que las funciones trascendentales elementales incluyen la función exponencial, las funciones logarítmicas y las funciones trigonométricas. Luego detalla diferentes casos y métodos para integrar funciones trigonométricas elevadas a exponentes, incluido el uso de identidades trigonométricas y cambios de variable.

1. Funciones Trascendentales
Es una función que no satisface una ecuación polinomial
cuyos coeficientes sean a su vez polinomios; esto contrasta
con las funciones algebraicas, las cuales satisfacen dicha
ecuación. En otras palabras, una función trascendente es
una función que trasciende al álgebra en el sentido que no
puede ser expresada en términos de una secuencia infinita
de operaciones algebraicas de suma, resta y extracción de
raíces. Una función de una variable es trascendente si es
independiente en un sentido algebraico de dicha variable.
Son funciones trascendentales elementales
Función exponencial

2. Sea a un número real positivo. La función
que a cada número real xle hace
corresponder la potencia ax
se llama función
exponencial de base a y exponente x.
Funciones logarítmicas

3. La función logarítmica en base a es la
función inversa de la exponencial en base a.

4. Funciones trigonométricas
La funciones trigonométricas asocian a
cada número real, x, el valor de la razón
trigonométrica del ángulo cuya medida en
radianes es x.
Función seno
f(x) = sen x
Función coseno
f(x) = cosen x

5. Función tangente
f(x) = tg x
Función cosecante
f(x) = cosec x

6. Función secante
f(x) = sec x

7. Función cotangente
f(x) = cotg x

12. Integrales Trigonométricas
Son aquellas integrales que tienen funciones
trigonométricas elevadas a exponentes. Para su mejor
comprensión se ha separado en diferentes casos.
Caso 1
Integrales de la forma

13. Identidad trigonométrica
cos2 x + sen2 x =1
Protocolo a seguir

15. Caso 2
Integrales de la forma
La identidad trigonométrica
Protocolo a seguir:

16. Ejemplo
Caso 3
Integrales de la forma

17. Identidad trigonométrica
cos2 x + sen2 x =1
a.- Cuando los dos son impares se toma al menor para
que la integral quede mas sencilla
b.- Cuando los dos son pares

18. Ejemplo
Caso 4
Integrales de la forma
También funciona para las funciones
cosecante, cotangente.
Identidad trigonométrica

19. tg2 x +1 = sec2 x
cTg2 x +1 = csc2 x
Protocolo a seguir según el caso:
1. 1.- Si la potencia de la secante es positiva y par, se queda
un factor de la secante al cuadrado y se convierte los
restantes en tangente. Al igual que en el caso 1 se fuerza
un cambio de variable

20. 2. Si la potencia de la tangente es positiva e impar, se
queda un factor secante –tangente (funciona como la
derivada) y convertir el resto en secante.
1.
3.3-Si no hay factores de la secante y la potencia de
tangente es positiva, se convierte un factor tangente
cuadrado en secante. Se desarrolla y se repite el proceso
tantas veces Como sea necesario

21. 4. Si la integral es de la forma , con n impar y
positivo, se usa la integración por partes.
5. Si no se aplica ninguno de estos casos, se convierte en
integral seno coseno.
Ejemplo

23. Casos especiales

24. Integrales Exponencial y Logarítmicas
Integrales exponenciales

25. Ejercicios
1
2

26. 3
4
4