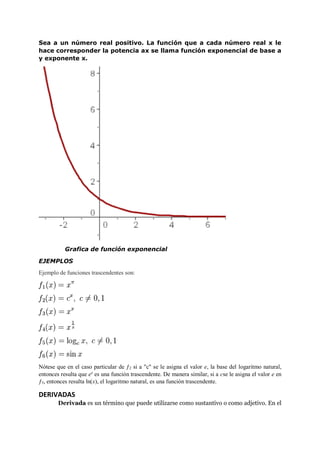
Este documento trata sobre funciones trascendentes y funciones trigonométricas. Explica que las funciones trascendentes son aquellas que no son algebraicas, e incluyen funciones exponenciales, trigonométricas, logarítmicas e hiperbólicas. Luego describe las funciones trigonométricas más comunes como seno, coseno y tangente, y provee una tabla con su dominio, rango y período. Finalmente, ofrece ejemplos de gráficas de funciones trascendentes como exponenciales, cosecante

1. Funciones Trascendentes:
Todas las funciones que se consideren como no algebraicas son denominadas
trascendentes. Mientras tanto las funciones exponenciales, trigonométricas,
logarítmicas e hiperbólicas, así como sus inversas, son funciones trascendentes.
En este punto y después de esa explicación técnica estoy seguro de que la duda
que ronda en sus mentes es ¿para que me sirve esto?. Estas funciones tienen
muchos usos sin embargo si queremos nombrar algunos ejemplos estas son y
pueden ser usadas para determinar el crecimiento de la población , el cálculo de
vibraciones y ondas, la eficiencia de algoritmos de computadora y muchas cosas
mas, por tal estas funciones son elementales y te seguirán a lo largo de la
carrera.
Funciones trigonométricas
Una función trigonométrica es importante por el hecho de tener un patrón y ser
repetitiva, esto le da la capacidad al que la utiliza de poder interpretar ciertos
actos físicos que requieren de cierta repetitividad para funcionar.
Las funciones trigonométricas mas utilizadas son: seno, coseno, tangente,
cotangente, secante, cosecante.
Basándonos en lo anterior te dejamos la siguiente tabla que muestra algunos
datos importantes de las funciones trigonométricas mas comunes:
FUNCIONES ABREVIATURA DOMINIO RANGO PERIODO
SENO SEN Los números
reales
[-1,1] 2π
COSENO COS Los números
reales
[-1,1] 2π
TANGENTE TAN Los reales
menos +π/2
-π2
Los números
reales
π
COTANGENTE COT Los reales
menos 0,π,-π
Los números
reales
π
SECANTE SEC Los reales
menos +π/2
-π2
Y,<-1 ,Y<1 2π
COSECANTE CSC Los reales
menos 0,π,-π
Y<-1 , Y<1 2π
Cuadro de funciones trigonométricas básicas
Graficas de la función seno, coseno y tangente

2. Función cosecante
f(x) = cosec x

3. Grafica de Función cosecante
Función cotangente
f(x) = cotg x
Grafica de función cotangente
Las funciones TRIGONOMÉTRICAS se definen en términos de los lados de
un triángulo rectángulo como se muestra a continuación:
Funciones exponenciales
f(x)= a^x

4. Sea a un número real positivo. La función que a cada número real x le
hace corresponder la potencia ax se llama función exponencial de base a
y exponente x.
Grafica de función exponencial
EJEMPLOS
Ejemplo de funciones trascendentes son:
Nótese que en el caso particular de ƒ2 si a "c" se le asigna el valor e, la base del logaritmo natural,
entonces resulta que ex
es una función trascendente. De manera similar, si a cse le asigna el valor e en
ƒ5, entonces resulta ln(x), el logaritmo natural, es una función trascendente.
DERIVADAS
Derivada es un término que puede utilizarse como sustantivo o como adjetivo. En el

5. primer caso, se trata de una noción de la matemática que nombra al valor límite del vínculo
entre el aumento del valor de una función y el aumento de la variable independiente.
La derivada, por lo tanto, representa cómo se modifica una función a medida que su entrada
también registra alteraciones. En los casos de las funciones de valores reales de una única
variable, la derivada representa, en un cierto punto, el valor de la pendiente de la recta
tangente al gráfico de la función en dicho punto.
a). – Solución
como sabemos el operador de derivada se distribuye sobre cada uno de los términos de las funciones,
es decir si entonces
por lo que para la función planteada en el ejercicio:
Recordando que la derivada de una función potencia es y que en la
derivada de una constante es cero tendremos
es decir
b). – Solución
Para este caso
Distribuyendo la derivada tenemos:

6. y utilizando directamente la fórmula para la cual es :
observamos que al derivar, por ejemplo, obtenemos por lo que
:
c). – Solución
De forma similar a los dos ejercicios anteriores obtenemos:
como sabemos si f(x)=a v(x) donde a es constante se obtiene
por lo tanto:
ULTIMO EJERCICIOS

7. INTEGRALES
La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una
integral es una generalización de lasuma de infinitos sumandos, infinitamente pequeños.
El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso
de integración o anti derivación, es muy común en la ingeniería y en la ciencia también; se utiliza
principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried
Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema
fundamental del cálculo integral, que propone que la derivación y la integración son procesos inverso
Dada una función de una variable real y un intervalo de la recta real, la integral es igual
al área de la región del plano limitada entre la gráfica de , el eje , y las líneas verticales
y , donde son negativas las áreas por debajo del eje .
La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya
derivada es la función dada . En este caso se denomina integral indefinida, mientras que las integrales
tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre
integrales primitivas e indefinidas.
Ejemplos
La aplicación de la segunda fórmula
Se aplica nuevamente la fórmula anterior combinada con la propiedad antes descrita

8. Enlace para la explicación sobre exponentes
-->

9. Cuando el grado del numerador es mayor o igual es denominador, se debe realizar una
división de polinomios