Este documento explica las funciones trigonométricas seno, coseno y tangente. Define sus dominios, rangos y períodos. Proporciona ejemplos de cómo calcular valores máximos y mínimos usando estas funciones. También incluye preguntas de ejemplo sobre el cálculo del rango de funciones seno multiplicadas por constantes.

1. DOMINIO
MATEMÁTICO
Bienvenidos

2. Funciones
Trigonométricas
DOMINIO MATEMÁTICO
2

3. Función Seno (Sen , Sin )
f(x) = sen (x)
3
DOMINIO: (-∞ ; ∞)
RANGO: −1; 1
Periodo: 2𝜋
CRECIENTE: 0;
𝜋
2
𝑈
3𝜋
2
DECRECIENTE:
𝜋
2
;
3𝜋
2

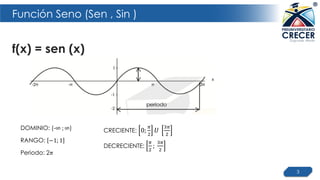
4. Función Seno (Sen , Sin )
Ejemplo
4
Una armadura está formada en su mayoría por triángulos que le ofrecen un mayor
soporte, se ha colocado una carpeta asfáltica sobre la armadura cuya altura está
definida por la función f(x)= 5 sen(x)+18, determine la altura máxima a la cual se
puede ubicar la carpeta asfáltica.
Recorrido de la función seno -1 ≤ senx ≤ 1
𝜋
2
, 1
Reemplazar punto máximo en la función
f
𝜋
2
= 5 ∗ 𝑠𝑖𝑛
𝜋
2
+ 18
f
𝜋
2
= 5 (1) + 18
f
𝜋
2
= 23
Se tiene que colocar a una altura máxima de 23 [L]
Punto
máximo

5. Función Coseno (Cos)
f(x)=cos(x)
5
DOMINIO: (-∞ ; ∞)
RANGO: −1; 1
Periodo: 2𝜋
CRECIENTE: 𝜋; 2𝜋
DECRECIENTE: 0; 𝜋

6. Función Coseno (Cos)
Ejemplo
En el análisis de las vibraciones generadas cuando los vehículos
pasan sobre un puente, se obtuvieron miles de datos los cuales al
ingresar al software informático, mostraron la siguiente tendencia.
6

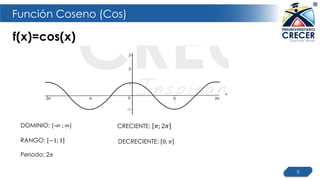
7. Función Coseno (Cos)
El ingeniero encargado de interpretar el gráfico llega a la siguiente
conclusión; que solamente se debe realizar un estudio en el domio
en el cual los valores de la amplitud sean diferentes. ¿Cuál es ese
dominio?
7
El dominio donde la amplitud es diferente es en el intervalo de [0,π]

8. Función tangente (tan)
8
f(x)=Tan(x) DOMINIO: (-∞ ; ∞)-
(2𝑘−1)𝜋
2
RANGO: (−∞; ∞)
PERIODO: 𝜋
MONOTONÍA: creciente en
todo su dominio
ASÍNTOTAS:
(2𝑘−1)𝜋
2

9. Ejemplos
La altura de una planta endémica de la amazonia en condiciones
normales está dada por h(t)= 5/2 cos(t)+ 5/2 , con base a la función.
Determine la altura máxima que una planta endémica puede
alcanzar, considerando que la base de la planta coincide con el eje
de las abscisas.
•
Punto
máximo
Punto
máximo
(0,1) (2𝜋, 1)
Reemplazamos en
cualquier punto
máximo:
ℎ 0 = 5/2 cos 0 + 5/2
h(0)=5/2 (1) + 5/2
h(0)= 5
a)5 b)10 c)5/2

10. Ejemplo
Se conoce que el recorrido de la función f(x)=sen(x) se encuentra
entre los valores [-1, 1]. ¿Cuál será el intervalo del recorrido de la
función f(x)=4*sen(x)?
a) [-1, 1] b) [0, 4] c) [-4, 4]
f(x)=senx
f(x)=4*senx

11. Ejemplo
Se conoce que el recorrido de la función f(x)=sen(x) se encuentra
entre los valores [-1, 1]. ¿Cuál será el intervalo del recorrido de la
función f(x)=sen(3x)?
a) [-1, 1] b) [0, 3] c) [-3, 3]
f(x)=senx
f(x)=sen(3x)

12. ¡ASEGURA TU INGRESO A LA U!
A NIVEL NACIONAL
www.aseguratuingresoalau.com
099 871 5726