Este documento resume las principales funciones trigonométricas (seno, coseno, tangente, cosecante, secante y cotangente) y sus propiedades. Incluye ejemplos de cómo estudiar estas funciones para una variable dada, encontrar su dominio, recorrido, período, puntos de corte, máximos y mínimos. También presenta ejemplos de funciones de valor absoluto y cómo representarlas gráficamente.

1. Bachiller:
Bustamante G. Jesús M
ITS Sistema SAIA
Barcelona, 2.014

2. FUNCIONES TRIGONOMETRICAS
Una función trigonométrica,
también llamada circular, es
aquella que se define por la
aplicación de una razón
trigonométrica a los distintos
valores de la variable
independiente, que ha de estar
expresada en radianes. Existen
seis clases de funciones
trigonométricas: seno y su
inversa, la cosecante; coseno y
su inversa, la secante; y
tangente y su inversa, la
cotangente. Para cada una de
ellas pueden también definirse
funciones circulares inversas

3. PROPIEDADES DE LAS FUNCIONES
TRIGONOMÉTRICAS
 Como características importantes y distintivas de las
funciones trigonométricas, se pueden resaltar las
siguientes:
 Las funciones seno, coseno y tangente son de naturaleza
periódica, de manera que el periodo de las funciones
seno y coseno es 2p y el de la función tangente es p.
 Las funciones seno y coseno están definidas para todo el
conjunto de los números reales. Ambas son funciones
continuas (no así la función tangente).
 Las funciones seno y coseno están acotadas, ya que sus
valores están contenidos en el intervalo [-1,1]. La
función tangente no está acotada. Las funciones seno y
tangente son simétricas respecto al origen, ya que sen (-
x) = -sen x; tg (-x)=-tg x. En cambio, la función coseno
es simétrica respecto al eje Y: cos (-x) = cos x.

4. FUNCIONES TRIGONOMETRICAS
LA FUNCIÓN SENO: Se denomina función seno, y se denota
por f (x) 5 sen x, a la aplicación de la razón trigonométrica
seno a una variable independiente x expresada en radianes.
La función seno es periódica, acotada y continua, y su
dominio de definición es el conjunto de todos los números
reales.
LA FUNCIÓN COSECANTE puede calcularse como la inversa
de la función seno expresada en radianes.
Gráfica de la Función Seno

5. FUNCIONES TRIGONOMETRICAS
EJERCICIO DE FUNCIÓN SENO
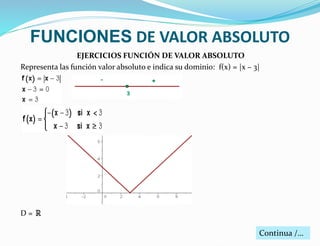
Dada la siguiente función y = sen (5x), estudia todas sus características. Representa su
gráfica.
1) Dominio: Dom(f ) = R
2) Recorrido: Im(f ) = [-1 , 1]
3) Periodicidad:
Como la función seno es periódica de período 2π, la función f(x) = sen (5x) es periódica
de período:
2π = 5x ⇔ x = 2π/5
Es periódica de período 2π/5 .
También podemos hallar el período de la función así:
f(x) = sen(5x) = sen(5x + 2π) = sen[ 5 (x + 2π/5) ] = f(x + 2π/5)
También podemos calcular el periodo de forma más fácil aplicando directamente la
siguiente fórmula:
Periodo = 2π/5
Continua /…

6. FUNCIONES TRIGONOMETRICAS
…/EJERCICIO DE FUNCIÓN SENO
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen 0 ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen (5x) ⇒ 5x = 0 ó 5x = π ⇒ x = 0 ó x = π/5 ⇒ (0 , 0) , (π/5 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
1 = sen (5x) ⇒ 5x = π/2 ⇒ x = π/10 ⇒ (π/10 , 1)
Los puntos mínimos de la función vendrán dados por la ecuación:
-1 = sen (5x) ⇒ 5x = 3π/2 ⇒ x = 3π/10 ⇒ (3π/10 , -1)
GRÁFICA:

7. FUNCIONES TRIGONOMETRICAS
LA FUNCIÓN COSENO: La función coseno, que se denota por
f (x) = cos x, es la que resulta de aplicar la razón
trigonométrica coseno a una variable independiente x
expresada en radianes. Esta función es periódica, acotada y
continua, y existe para todo el conjunto de los números
reales.
LA FUNCIÓN SECANTE se determina como la inversa de la
función coseno para un ángulo dado expresado en radianes.
Gráfica de la Función Coseno

8. FUNCIONES TRIGONOMETRICAS
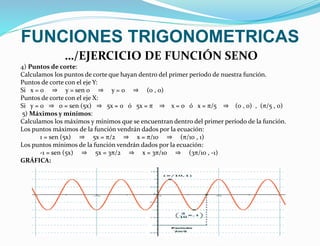
EJERCICIO DE FUNCIÓN COSENO
Dada la siguiente función y = 2 cos(x), estudia todas sus características. Representa su
gráfica.
1) Dominio: Dom(f ) = R
2) Recorrido: Im(f ) = [-2 , 2]
3) Periodicidad:
Como la función coseno es periódica de período 2π , la función f(x) = 2 cos(x) tiene el
mismo período: 2π
También podemos sacar el período de la función así:
f(x) = 2 cos(x) = 2 cos(x + 2π) = f(x + 2π)
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 ⇒ y = 2 ⇒ (0 , 2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos(x) ⇒ cos(x) = 0 ⇒ x = π/2 ó x = 3π/2
Luego los puntos de corte con el eje X son: (π/2 , 0) , (3π/2 , 0)
Continua /…

9. FUNCIONES TRIGONOMETRICAS
…/EJERCICIO DE FUNCIÓN COSENO
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la
función.
Los puntos máximos de la función vendrán dados por la ecuación:
2 = 2 cos(x) ⇒ 1 = cos(x) ⇒ x = 0 ó x = 2π ⇒ (0 , 2) , (2π , 2)
Los puntos mínimos de la función vendrán dados por la ecuación:
-2 = 2 cos(x) ⇒ -1 = cos(x) ⇒ x = π ⇒ (π , -2)
GRÁFICA:

10. FUNCIONES TRIGONOMETRICAS
LA FUNCIÓN TANGENTE: Se define función tangente de una
variable numérica real a la que resulta de aplicar la razón
trigonométrica tangente a los distintos valores de dicha variable.
Esta función se expresa genéricamente como f (x) = tg x, siendo x
la variable independiente expresada en radianes.
LA FUNCIÓN COTANGENTE es la inversa de la tangente, para
cualquier ángulo indicado en radianes.
Gráfica de la Función Tangente

11. FUNCIONES TRIGONOMETRICAS
EJERCICIO DE FUNCIÓN TANGENTE
Dada la siguiente función y = tg(x/4), estudia todas sus características e indica sus asíntotas.
Representa su gráfica.
1) Dominio:
La función tangente no está definida en: (2k + 1)π/2 , k ∈ Z
Por tanto, nuestra función tampoco estará definida en:
x/4 = (2k + 1)π/2 k ∈ Z ⇔ x = 2(2k + 1)π , k ∈ Z
Luego: Dom(f ) = R - { 2(2k + 1)π | k ∈ Z }
2) Recorrido: Im(f ) = R
3) Periodicidad:
Como la función tangente es periódica de período π , la función f(x) = tg (x/4) es periódica
de período:
x/4 = π ⇔ x = 4π
Es periódica de período 4π .
También podemos sacar el período de la función así:
Continua /…

12. FUNCIONES TRIGONOMETRICAS
…/EJERCICIO DE FUNCIÓN TANGENTE
También podemos calcular el periodo de forma más fácil aplicando directamente la
siguiente fórmula:
4) Puntos de corte:
Puntos de corte con el eje Y:
x = 0 ⇒ y = tg(x/4) ⇒ y = tg(0) ⇒ y = 0 ⇒ (0 , 0)
Sabemos que la función tangente corta al eje X en: 0 = tg(x) ⇔ x = 0 ó x = π
En nuestro caso: 0 = tg(x/4) ⇔ x = 0 ó x/4 = π ⇔ x = 0 ó x = 4π
Como el período de nuestra función es 4π , los puntos de corte con el eje X en el primer
período son: (0 , 0) , (4π , 0)
5) Máximos y mínimos:
La función tangente no tiene máximos ni mínimos, por tanto, f(x) = tg(x/4) tampoco los
tiene.
GRÁFICA:

13. FUNCIONES TRIGONOMETRICAS
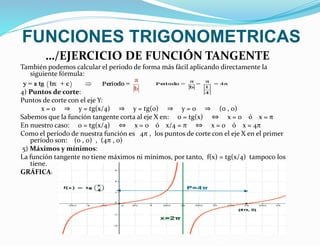
EJERCICIO DE FUNCIÓN SECANTE
Dada la siguiente función y = 3 sec(x), estudia todas sus características e indica sus asíntotas.
Representa su gráfica.
1) Dominio:
La función cos(x) es cero en:
tanto, el dominio de nuestra función vendrá dado por:
2) Recorrido:
Sabemos que el recorrido de la función coseno es [-1 , 1] . Es decir: - 1 ≤ cos(x) ≤ 1
Separamos las dos desigualdades y, operando, tratamos de "conseguir" nuestra función:
Luego: - 3 ≥ f(x) , que representa el intervalo (-∞ , - 3]
Luego: f(x) ≥ 3 , que representa el intervalo [3 , ∞)
Por tanto, el recorrido o imagen de nuestra función es: Im(f ) = (-∞ , - 3] ∪ [3 , ∞)
3) Periodicidad:
Como la función secante es periódica de período π , la función f(x) = 3 sec(x) tiene el mismo
período: π .
También podemos sacar el período de la función así: f(x) = 3 sec(x) = 3 sec(x + π) = f(x + π)
Continua /…

14. FUNCIONES TRIGONOMETRICAS
…/EJERCICIO DE FUNCIÓN SECANTE
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra
función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 3 sec 0 ⇒ y = 3·1 = 3 ⇒ (0 , 3)
No tiene puntos de corte con el eje X, puesto que: y = 0 ∉ Im(f ) = (-∞ , - 3] ∪ [3 , ∞)
5) Máximos y mínimos:
La función sec(x) no tiene ni máximos ni mínimos absolutos, por tanto, la función
f(x) = 3 sec(x) tampoco.
GRÁFICA:

15. FUNCIONES DE VALOR ABSOLUTO
La definición del valor
absoluto surge de
nociones geométricas, y
se relaciona con los
conceptos de longitud y
distancia. Tiene por
ecuación f(x) = |x|, y
siempre representa
distancias; por lo tanto,
siempre será positiva o
nula, su gráfica no se
encontrará jamás debajo
del eje x.
Las funciones en valor absoluto
se transforman en funciones
a trozos, siguiendo los
siguientes pasos:
 1. Se iguala a cero la función,
sin el valor absoluto, y se
calculan sus raíces.
 2. Se forman intervalos con
las raíces y se evalúa el signo
de cada intervalo.
 3. Definimos la función a
trozos, teniendo en cuenta
que en los intervalos donde
la x es negativa se cambia el
signo de la función.

16. FUNCIONES DE VALOR ABSOLUTO
EJERCICIOS FUNCIÓN DE VALOR ABSOLUTO
Representa la función valor absoluto: f(x) = |x − 2|
f(x) = |x − 2|
Continua /…

17. FUNCIONES DE VALOR ABSOLUTO
EJERCICIOS FUNCIÓN DE VALOR ABSOLUTO
Representa las función valor absoluto e indica su dominio: f(x) = |x − 3|
D =
Continua /…

18. FUNCIONES DE VALOR ABSOLUTO
EJERCICIOS FUNCIÓN DE VALOR ABSOLUTO
Representa las función valor absoluto e indica su dominio:
D =
Continua /…

19. FUNCIONES DE VALOR ABSOLUTO
EJERCICIOS FUNCIÓN DE VALOR ABSOLUTO
Representa la función valor absoluto:
f(x) = |x| − x
x = 0
Continua /…

20. FUNCIONES DE VALOR ABSOLUTO
EJERCICIOS FUNCIÓN DE VALOR ABSOLUTO
Representa la función valor absoluto:
f(x) = |x| / x
x = 0