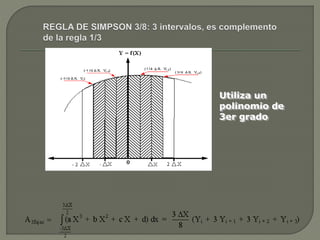
El documento describe el método de Simpson para estimar integrales. La regla de Simpson proporciona una mejor aproximación que la regla del trapecio al ajustar un polinomio de tercer grado en lugar de una línea recta. También presenta un ejemplo de cómo aplicar la regla de Simpson de 1/3 para evaluar una doble integral definida.

1. REGLAS DE SIMPSON
Métodos Numéricos

2.  Regla de Simpson
• Introducción
• De 1 / 3
• De 3 / 8
 Desarrollo de problemas
• Manualmente
• Mediante Matlab

4.  Es un método para estimar el resultado de una
integral.
 Es una mejor aproximación a la regla
Trapezoidal, sin incurrir en un mayor número
de subdivisiones.
 Ajusta una curva de orden superior en lugar
de una línea recta como en la regla
trapezoidal

7. a b
a b
Regla trapezoidal
Aproximación a la Regla trapezoidal.
Polinomio de Segundo orden
o
o
o
 )()(4)(
3
b
a dxf(x) 210 xfxfxf
h
 = ancho* altura promedio

8. Utiliza un
polinomio de
3er grado

9.  )()(3)(3)(
8
3b
a dxf(x) 3210 xfxfxfxf
h

a b
o
o
o
o
Polinomio de tercer orden
a b
o
o
o
o
Regla trapezoidal
= ancho* altura promedio

10. •Son métodos de aproximación
•El error es inversamente proporcional al número de
subintervalos
•El método de simpson da una solución más aproximada
•Permiten elaboración de un algoritmo y codificar un
programa

11.  “Descripción del problema 2”
Utilice la regla de 1/3 Simpson para evaluar la doble integral.
Los límites de integración son: a=1, b=3, c(x)= ln(x), d(x)= 3 + exp(x/5).
  
a
b
xd
xc
dydxyxI
)(
)(
)sin(

12.  “Solución matemática problema 2”



exp(x/5)3
ln(x),
)sin()( dyyxixif

3
1
)( dxxifI
   
6
)(4
)( 210 xfxfxf
abI


Para aplicar la regla de Simpson puede hacer la siguiente sustitución:
Por lo que se obtiene:
Aplicando la regla de Simpson se obtiene:

13. Los puntos son los siguientes:
X0 = 1; X1= 2 ; X2=3
Por lo tanto sustituyendo (*) en (**). Obtenemos:
6
)sin()sin(4)sin(
)(
exp(x/5)3
ln(x),
exp(x/5)3
ln(x),
exp(x/5)3
ln(x),




dyyxidyyxidyyxi
abI
6
)3sin()2sin(4)1sin(
)13(
exp(3/5)3
ln(3),
exp(2/5)3
ln(2),
exp(1/5)3
ln(1),




dyydyydyy
I

14. 06458.0)1sin(
2214.4
0,
1   dyyI
1086.2)2sin()2sin(
4918.4
0.6931
exp(2/5)3
ln(2),
2  

dyydyyI
67454.0)3sin()3sin(
8211.4
1.0986
exp(3/5)3
ln(3)
3  

dyydyyI
0148.3
6
67454.0)1086.2(4064581.0
)13(



I
I

15.  “Solución en Matlab problema 2”

16.  Por cálculos
Programado

17.  Para los datos de
máximo punto del
volumen en un
tanque, tabulados en
una fábrica de jugos y
medidos por un
sensor cada cierto
tiempo
Datos tabulados
t f(t)
1,6 4,593
1,8 6,05
2 7,389
2,2 9,025
2,4 11,023
2,6 13,464
2,8 16,445
3 20,066
3,2 24,533
3,4 29,964

18.  n-1
I = (b-a)[2∑ f(xi) + f(xn)]/2n
i=1
I = (3,4-1,6) 4,593+2*(108,015 +29,964)
2*18
I = 25,0547

19.  I1 = (0,6)*4,593+3(6,050)+3(7,389)+9,025
8
 I1 = 4,045125
 I2 = (0,6)*9,025+3(11,023)+3(13,464)+16,445
8
 I2 = 7,4198
 I3 =(0,6)*16,445+3(20,086)+3(24,533)+29,964
8
 I3 = 13,1449
 I = 24,6099