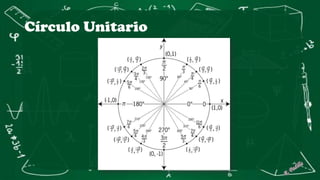
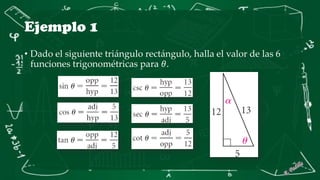
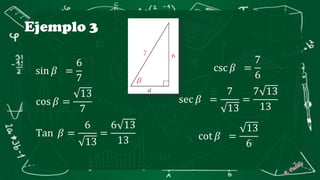
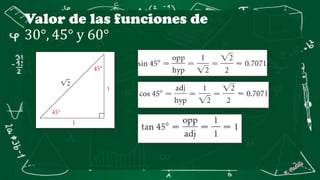
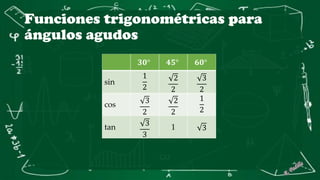
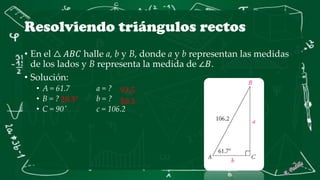
Este documento presenta conceptos básicos de trigonometría en triángulos rectángulos. Explica las seis funciones trigonométricas (seno, coseno, tangente, cosecante, secante y cotangente) y cómo se calculan en función de los lados del triángulo. Incluye ejemplos numéricos para ilustrar el cálculo de las funciones trigonométricas. También cubre conceptos como ángulos complementarios y cofunciones.

1. Trigonometría en el
triángulo rectángulo
Prof. Rosa E. Padilla Torres
𝐶𝑜𝑠(𝜃)
𝐶𝑜𝑡(𝜃)

2. Círculo Unitario

3. Proporciones trigonométricas
• Ángulo agudo: Un ángulo agudo es un ángulo cuya medida es
mayor de 0° y menor de 90°.
• Las letras griegas son utilizadas para identificar ángulos:
• 𝛼 (alpha)
• 𝛽 (beta)
• 𝛾 (gamma)
• 𝜃 (theta)
• 𝜙(phi)

4. Proporciones trigonométricas
𝜃
Lado adyacente a 𝜃
Lado
opuesto a 𝜃

5. Proporciones trigonométricas
• El largo de los lados del triángulo son utilizados para definir las
proporciones trigonométricas:
• Seno (sin)
• Coseno (cos)
• Tangente (tan)
• Cosecante (csc)
• Secante (sec)
• Cotangente (cot)

6. Seno de 𝜽
• El seno de 𝜃 corresponde al largo del lado opuesto de 𝜃
dividido entre el largo de la hipotenusa.
• 𝑆𝑖𝑛 𝜃 =
medida del lado opuesto a 𝜃
medida de la hipotenusa
• Sin(𝜃)
𝜃
Adyacente
Opuesto

7. Coseno de 𝜽
• El coseno de 𝜃 corresponde al largo del lado adyacente de 𝜃
dividido entre el largo de la hipotenusa.
• 𝐶𝑜𝑠 𝜃 =
medida del lado adyacente a 𝜃
medida de la hipotenusa
• Cos(𝜃)
𝜃
Adyacente
Opuesto

8. Funciones trigonométricas
𝜃
Adyacente
Opuesto
𝐶𝑜𝑠 𝜃 =
adyacente a 𝜃
hipotenusa
𝑆𝑖𝑛 𝜃 =
opuesto a 𝜃
hipotenusa
𝑇𝑎𝑛 𝜃 =
opuesto a 𝜃
adyacente a 𝜃
𝑆𝑒𝑐 𝜃 =
hipotenusa
adyacente a 𝜃
𝐶𝑠𝑐 𝜃 =
hipotenusa
opuesto a 𝜃
𝐶𝑜𝑡 𝜃 =
adyacente a 𝜃
opuesto a 𝜃

9. Ejemplo 1
• Dado el siguiente triángulo rectángulo, halla el valor de las 6
funciones trigonométricas para 𝜃.

10. Ejemplo 2
• Halla el valor de las 6 funciones trigonométricas para 𝛼.

11. Ejercicios de práctica
• Halla la proporción de las 6 funciones trigonométricas para
cada caso. Simplifica a su mínima expresión.
1) 2) 3) 4) 5)
6) 7) 8) 9) 10)

12. Triángulos semejantes
• Se dice que dos triángulos son semejantes si los ángulos
correspondientes tienen la misma medida.
• El largo de los lados de los triángulos tienen la misma
proporción.

13. Ejemplo 3
• Utiliza a información provista para hallar los valores de las seis
funciones trigonométricas.
𝑎² + 𝑏² = 𝑐²
𝑎² + 6² = 7²
𝑎² + 36 = 49
𝑎² = 49 − 36 = 13
𝑎 = 13

14. Ejemplo 3
sin 𝛽 =
6
7
cos 𝛽 =
13
7
Tan 𝛽 =
6
13
=
6 13
13
csc 𝛽 =
7
6
sec 𝛽 =
7
13
=
7 13
13
cot 𝛽 =
13
6

15. Valor de las funciones de
30°, 45° y 60°

16. Ejemplo 4
𝑎² + 𝑏² = 𝑐²
𝑎² + 1² = 2²
𝑎² + 1 = 4
𝑎² = 4 − 1 = 3
𝑎 = 3

17. Ejemplo 4
• Halla los valores de las funciones trigonométricas para 30° y 60°
sin 30° =
1
2
= 0.5
cos 30° =
3
2
≈ 0.8660
tan 30° =
1
3
=
3
3
≈ 0.5774
cos 60° =
1
2
= 0.5
sin 60° =
3
2
≈ 0.8660
tan 60° =
3
1
= 3 ≈ 1.7321

18. Funciones trigonométricas para
ángulos agudos
𝟑𝟎° 𝟒𝟓° 𝟔𝟎°
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1 3

19. Ejemplo 5
• Altura del globo

20. Ejemplo 5
• Altura del globo
tan 30° =
opuesto
adyacente
=
ℎ
1.2
1.2 ∙ tan 30° = ℎ
1.2
3
3
= ℎ
ℎ ≈ 0.7
El globo está a aproximadamente
0.7 millas de alto.

21. Ejemplo 6
• Un pintor desea colocar su escalera expandible a un máximo de
25 pies. La misma se encuentra a una separación de 6.5 pies de
la pared.
• ¿Qué ángulo se forma
entre la escalera y el piso?

22. Ejemplo 6
• Un pintor desea colocar su escalera expandible a un máximo de
25 pies. La misma se encuentra a una separación de 6.5 pies de
la pared.
• ¿Qué ángulo se forma
entre la escalera y el piso?
cos 𝜃 =
adyacente
hipotenusa
=
6.5
25
= 0.26
cos−1
0.26 ≈ 74.92993786°

23. Cofunciones y complementos
• Dos ángulos son complementarios si la suma de sus medidas es
90°.
• La suma de las medidas de los ángulos interiores de un
triángulo es de 180°.
• Uno de los ángulos mide 90°.
• Uno de los ángulos mide 𝜃.
• El otro de los ángulos mide 90° − 𝜃.

24. Identidades de Cofunciones
sin 𝜃 = cos 90° − 𝜃 cos 𝜃 = sin 90° − 𝜃
tan 𝜃 = co𝑡 90° − 𝜃 cot 𝜃 = tan 90° − 𝜃
sec 𝜃 = csc 90° − 𝜃 csc 𝜃 = sec 90° − 𝜃

25. Ejemplo 7
• Dado que:
• sin 18° ≈ 0.3090,
• cos 18° ≈ 0.9511,
• tan 18° ≈ 0.3249
• Halla el valor de las seis funciones trigonométricas para 72°.

26. Ejemplo 7
sin 18° ≈ 0.3090
cos 18° ≈ 0.9511
tan 18° ≈ 0.3249
csc 18° =
1
sin 18°
≈ 3.2361
sec 18° =
1
cos 18°
≈ 1.0515
cot 18° =
1
tan 18°
≈ 3.0777

27. Ejemplo 7
sin 72° = cos 18° ≈ 0.9511
cos 72° = sin 18° ≈ 0.3090
tan 72° = cot 18° ≈ 3.0777
csc 72° = sec 18° ≈ 1.0515
sec 72° = csc 18° ≈ 3.2361
cot 72° = tan 18° ≈ 0.3249

28. Ejercicios de práctica
• Halla el valor de las seis funciones trigonométricas para el
ángulo indicado.

29. Ejercicios de práctica
• Halla el valor de las seis funciones trigonométricas para el
ángulo indicado.

30. Ejercicios de práctica
7. Dado que sin 𝛼 =
5
3
, cos 𝛼 =
2
3
, tan 𝛼 =
5
2
halla
csc ∝, sec ∝ y cot ∝ .
8. Dado que sin 𝛽 =
2 2
3
, cos 𝛽 =
1
3
, tan 𝛽 = 2 2, halla
csc 𝛽, sec 𝛽 y cot 𝛽 .

31. Ejercicios de práctica
Dado el valor de un ángulo agudo, halla el valor de las otras
cinco funciones trigonométricas.
9. sin 𝜃 =
24
25
10. cos 𝜎 = 0.7 11. tan 𝜙 = 2
12 . cot 𝜃 =
1
3
13. csc 𝜃 = 1.5 14. sec 𝛽 = 17
15. cos 𝛽 =
5
5
16. sin 𝜎 =
10
11

32. Ejercicios de práctica
Halla el valor exacto para cada función.
17. cos 45° 18. tan 30° 19. sec 60°
20. sin 45° 21. cot 60° 22. csc 45°
23. sin 30° 24. cos 60° 25. tan 45°
26. sec 30° 27. csc 30° 28. cot 60°

33. Ejercicios de práctica
• Halla la medida de los lados faltantes.
1) 2) 3)
4) 5)

34. Aplicaciones de
triángulos rectos

35. Resolviendo triángulos rectos
• En el △ 𝐴𝐵𝐶 halle a, b y B, donde a y b representan las medidas
de los lados y B representa la medida de ∠𝐵.
• Solución:
• A = 61.7 a = ?
• B = ? b = ?
• C = 90˚ c = 106.2
28.3°
93.5
50.3

36. Ejemplo
• En △ 𝐷𝐸𝐹, halle D, F y d.
• Solución:
• D = ? d = ?
• E = 90° e = 23
• F = ? f = 13
55.58°
34.42°
19

37. Aplicaciones #1
• Ejemplo: Excursión al Gran Cañón
• Un mochilero se encuentra de excursión en el borde norte del Gran
Cañón, cuando nota una extraña formación de roca directamente a
través del Cañón.
• El mochilero decide continuar observando el punto de referencia a lo
largo del borde. En dos horas, ha recorrido 6.2 mi al este, y el punto
de referencia sigue a la vista en un ángulo de aproximadamente 50°
del borde norte.
• ¿Cuántas millas el mochilero caminó desde
la formación de rocosa?
• ¿Cuál lejos se encuentra del punto inicial?

38. Aplicaciones #1
Solución:
• c = 9.6 mi
• b = 7.4 mi

39. Aplicaciones #2
• Un fotógrafo aéreo quien toma fotos de granjas para una
compañía de bienes raíces.
• Las fotos son tomadas a aproximadamente 475 pies de altura a
una distancia de 850 pies de la casa de campo.
• ¿Cuál es el ángulo de depresión del avión a la casa?

40. Aplicaciones #2

41. Aplicaciones #3
• Altura de la nube
• Para medir la altura de una nube durante la noche, un rayo de
luz vertical es proyectado directamente en la nube. Desde un
punto a 135 pies de distancia de la fuente de luz, el ángulo de
elevación en dirección al punto formado en la nube es de 67.35°.
Determina la altura de la nube.

42. Aplicaciones #3

43. Ejercicios de práctica
Halla la distancia a través del río.

44. Ejercicios de práctica
𝑄𝑃𝐻 está formado, donde ∠𝑄𝑃𝐻 es 45°. Utiliza las funciones
trigonométricas para hallar la distancia de tercera a primera base.

45. Utiliza la medida del ángulo dado para
determinar la medida del lado indicado
1) 2) 3) 4)
5) 6) 7) 8)

46. Cofunciones

47. Cofunciones

48. Cofunciones