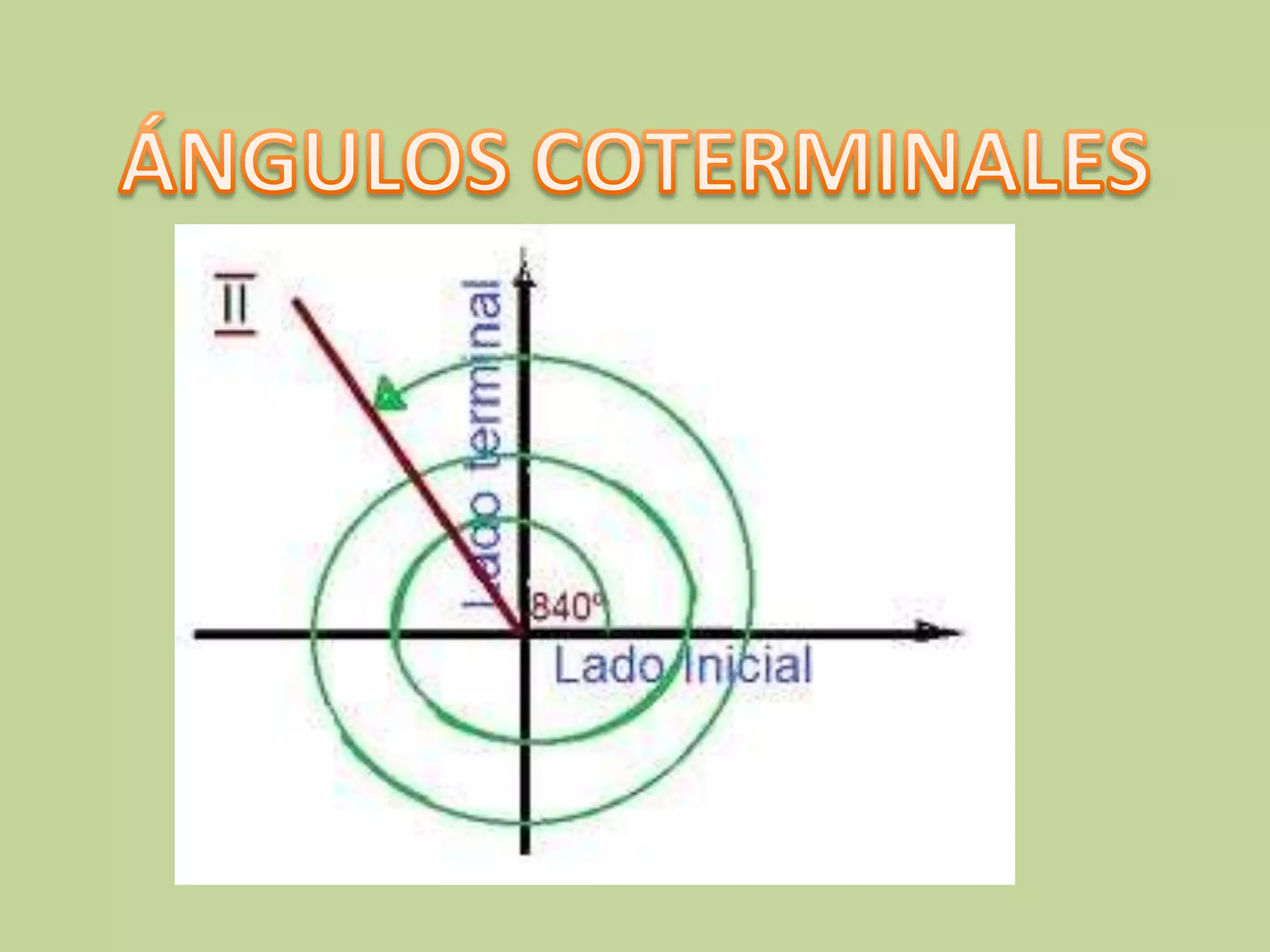
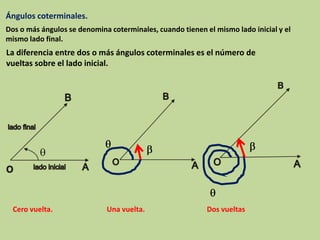
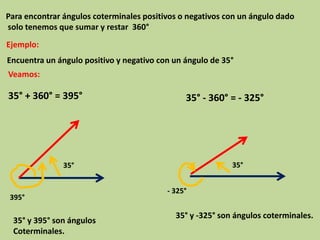
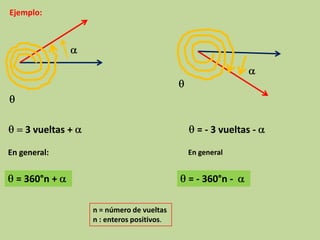
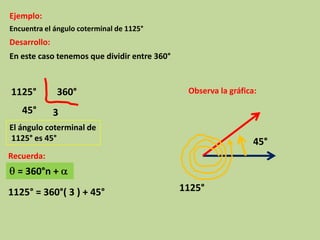
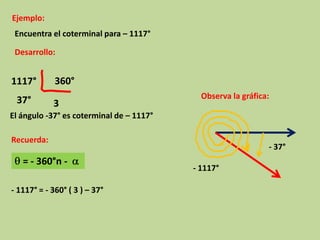
Este documento explica los ángulos coterminales. Dos o más ángulos son coterminales cuando comparten el mismo lado inicial y final. La diferencia entre ángulos coterminales es el número de vueltas completas sobre el lado inicial. Para encontrar ángulos coterminales positivos o negativos de un ángulo dado, se suma o resta 360 grados. Se proveen ejemplos para ilustrar cómo encontrar ángulos coterminales.

2. Ángulos coterminales.
Dos o más ángulos se denomina coterminales, cuando tienen el mismo lado inicial y el
mismo lado final.
La diferencia entre dos o más ángulos coterminales es el número de
vueltas sobre el lado inicial.
Cero vuelta. Una vuelta. Dos vueltas

3. Para encontrar ángulos coterminales positivos o negativos con un ángulo dado
solo tenemos que sumar y restar 360°
Ejemplo:
Encuentra un ángulo positivo y negativo con un ángulo de 35°
Veamos:
35° + 360° = 395° 35° - 360° = - 325°
35° 35°
- 325°
395°
35° y -325° son ángulos coterminales.
35° y 395° son ángulos
Coterminales.

4. Ejemplo:
3 vueltas + = - 3 vueltas -
En general: En general
= 360°n + = - 360°n -
n = número de vueltas
n : enteros positivos.

5. Ejemplo:
Encuentra el ángulo coterminal de 1125°
Desarrollo:
En este caso tenemos que dividir entre 360°
1125° 360° Observa la gráfica:
45° 3
El ángulo coterminal de
1125° es 45° 45°
Recuerda:
= 360°n +
1125° = 360°( 3 ) + 45° 1125°

6. Ejemplo:
Encuentra el coterminal para – 1117°
Desarrollo:
1117° 360°
Observa la gráfica:
37° 3
El ángulo -37° es coterminal de – 1117°
Recuerda:
- 37°
= - 360°n -
- 1117°
- 1117° = - 360° ( 3 ) – 37°

7. Practicando lo aprendido:
Encuentra un ángulo positivo y negativo para los siguientes ángulos:
1) 36° 15) 1470°
2) 50° 16) 780°
3) 14° 17) 2217°
4) 100° 18) - 2940°
5) 70° 19) - 1845°
6) 80° 20) - 2550°
7) 120°
8) - 40°
9) - 15°
10) - 65°
11) - 36°
12) - 48°
13) - 75°
14) - 80°