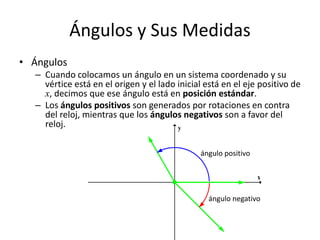
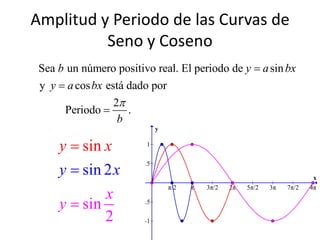
Este documento trata sobre ángulos y funciones trigonométricas. Explica cómo se definen y miden los ángulos, así como las funciones trigonométricas básicas como seno, coseno y tangente. También cubre temas como ángulos coterminales, complementarios y suplementarios, así como conversiones entre grados y radianes.

1. Funciones Trigonométricas
MATH1500

2. Ángulos y Sus Medidas
• Ángulos
– Un ángulo es determinado al rotar un rayo sobre
su extremo.
– La posición inicial del rayo se conoce como el lado
inicial del ángulo y la posición del rayo después de
la rotación es el lado terminal.
lado inicial
vértice

3. Ángulos y Sus Medidas
• Ángulos
– Cuando colocamos un ángulo en un sistema coordenado y su
vértice está en el origen y el lado inicial está en el eje positivo de
x, decimos que ese ángulo está en posición estándar.
– Los ángulos positivos son generados por rotaciones en contra
del reloj, mientras que los ángulos negativos son a favor del
reloj.
x
y
ángulo positivo
ángulo negativo

4. Ángulos y Sus Medidas
• Ángulos
– Los ángulos son nombrados con letras griegas tales como
α, β y θ, también con letras mayúsculas tales como A, B y C.
– En la siguiente figura los ángulos α y β tienen el mismo
lado inicial y terminal; estos ángulos son llamados ángulos
coterminales.
x
y
x
y
α
β
α
β

5. Medida en Grados
• La medida de un ángulo está determinada por la
cantidad de rotación desde el lado inicial al lado
terminal.
• La unidad más común de medida de ángulos es el
grado, denotado por el símbolo °.

6. Encontrando Ángulos Coterminales
• Encuentra dos ángulos coterminales (uno
positivo y uno negativo) para:
a) θ = 390°
b) θ = -120°

7. Ángulos Complementarios y
Suplementarios
• Dos ángulos positivos α y β son
complementarios si su suma es 90°. Dos
ángulos positivos α y β son suplementarios si
su suma es 180°.
• Si es posible, encuentra el complemento y el
suplemento de:
a) 72°
b) 148°

8. Medida en Radianes
• Un radián (rad) es la medida de un ángulo central
θ que intercepta un arco s igual en longitud al
radio r del círculo.

9. Medida en Radianes
• La medida en radianes de un ángulo central θ
se obtiene dividiendo el largo de arco s por r.
s
r
 

10. Encontrando Ángulos
• Encuentra cada ángulo.
a) El complemento de θ = π/12
b) El suplemento de θ = 5π/6
c) Un ángulo coterminal a θ = 17π/6

11. Conversión de Medidas de Ángulos
• Convierte las siguientes medidas a radianes.
a) 135°
b) -270°
• Convierte las siguientes medidas a grados.
a) -π/2 rad
b) 2 rad
rad
Para convertir grados a radianes, multiplica los grados por .
180
180
Para convertir radianes a grados, multiplica los radianes por .
rad





12. Trigonometría del Triángulo Recto
θ
Lado adyacente a θ
Ladoopuestoaθ
opuesto
sin
hipotenusa
adyacente
cos
hipotenusa
opuesto
tan
adyacente






hipotenusa
csc
opuesto
hipotenusa
sec
adyacente
adyacente
cot
opuesto







13. Evaluando Funciones Trigonométricas
• Utilizando la figura provista encuentra el valor
exacto de las seis funciones trigonométricas
de θ.
4
3
θ

14. Senos, Cosenos y Tangentes de
Ángulos Especiales
1
sin30 sin
6 2

  
3
cos30 cos
6 2

  
3
tan30 tan
6 3

  
2
sin 45 sin
4 2

  
2
cos45 cos
4 2

   tan 45 tan 1
4

  
3
sin60 sin
3 2

  
1
cos60 cos
3 2

   tan60 tan 3
3

  

15. Identidades Trigonométricas
• Identidades Recíprocas
• Identidades Cocientes
• Identidades Pitagoreanas
• 1
1
sin
csc



1
cos
sec



1
tan
cot



1
csc
sin



1
sec
cos



1
cot
tan



sin
tan
cos




cos
cot
sin




2 2
2 2
2 2
sin cos 1
tan 1 sec
1 cot csc
 
 
 
 
 
 

16. Aplicando Identidades Trigonométricas
• Sea θ un ángulo agudo tal que cos θ = 0.8.
Encuentra el valor de:
a) sin θ
b) tan θ

17. Utilizando Identidades
Trigonométricas
• Utiliza identidades trigonométricas para
transformar un lado de la ecuación en el otro.
a) cos θ sec θ = 1
b) (sec θ + tan θ) (sec θ – tan θ) = 1

18. Aplicaciones que Envuelven Triángulos
Rectos
• Un agrimensor está parado a 50 pies de la base
de un árbol. El agrimensor mide el ángulo de
elevación al tope del árbol la cual es 71.5°. ¿Cuán
alto es el árbol?
50 ft
71.5°

19. Aplicaciones que Envuelven Triángulos
Rectos
• Te encuentras a 200 m de un río. En lugar de
caminar directamente hacia el río, caminas
400 m por una vereda que te lleva a la orilla
del río. Encuentra el ángulo entre la vereda y
el borde del río.

20. x
y
(x, y)
θ
Funciones Trigonométricas de
Cualquier Ángulo
 
2 2
Sea un ángulo en posición estándar con , un
punto en el lado terminal de y 0.
x y
r x y

   
r
sin
cos
tan
y
r
x
r
y
x






csc
sec
cot
r
y
r
x
x
y







21. Evaluando Funciones Trigonométricas
• Sea (-3, 4) un punto en el lado terminal de θ.
Encuentra el seno, coseno y tangente de θ.
• Sea (12, -5) un punto en el lado terminal de θ.
Encuentra el seno, coseno y tangente de θ.

22. Signos de las Funciones
Trigonométricas
x
y
Cuadrante I
sin :
cos :
tan :






Cuadrante II
sin :
cos :
tan :






Cuadrante III
sin :
cos :
tan :






Cuadrante IV
sin :
cos :
tan :







23. Evaluando Funciones Trigonométricas
2
1) Dado que sin y que tan 0, encuentra el valor
3
de las seis funciones trigonométricas.
15
2) Dado que tan y que sin 0, encuentra el valor
8
de las seis funciones trigonométricas.
 
 
  
  

24. Ángulos de Referencia
• Sea θ un ángulo en posición estándar. Su
ángulo de referencia es el ángulo agudo θ’
formado por el lado terminal de θ y el eje
horizontal.
• Encuentra el ángulo de referencia para los
ángulos dados
1. θ = 300°
2. θ = 2π/3
3. θ = -135°

25. Evaluando Funciones Trigonométricas
de Cualquier Ángulo
• Para encontrar el valor de una función trigonométrica de
cualquier ángulo θ:
1. Determina el valor de la función para el ángulo asociado de
referencia.
2. Dependiendo del cuadrante donde θ descansa, coloca el signo
apropiado al valor de la función.
(grados) 0 30 45 60 90 180 270
(radiannes) 0
6

4

3

2


3
2

sin 0
1
2
2
2
3
2
1 0 1
cos 1
3
2
2
2
1
2
0 1 0
tan 0
3
3
1 3 Indef. 0 Indef.

26. El Círculo Unitario
-1 1
-1
1
x
y
0
2


3
2


27. El Círculo Unitario
-1 1
-1
1
x
y
0
2


3
2

4
3
4

5
4
 6
4


28. El Círculo Unitario
-1 1
-1
1
x
y
0
2


3
2

4
3
4

5
4
 6
4

6

3
2
3

5
6

7
6

4
3
 5
3

11
6


29. El Círculo Unitario
-1 1
-1
1
x
y
0
2


3
2

4
3
4

5
4
 6
4

6

3
2
3

5
6

7
6

4
3
 5
3

11
6

 1,0
 0,1
 1,0
 0, 1
3 1
,
2 2
 
  
 
2 2
,
2 2
 
  
 
1 3
,
2 2
 
  
 
3 1
,
2 2
 
  
 
2 2
,
2 2
 
  
 
1 3
,
2 2
 
  
 
3 1
,
2 2
 
   
 
2 2
,
2 2
 
   
 
1 3
,
2 2
 
   
 
1 3
,
2 2
 
  
 
2 2
,
2 2
 
  
 
3 1
,
2 2
 
  
 

30. Funciones Trigonométricas de Ángulos
No Agudos
• Evalúa cada función trigonométrica.
 
4
1) cos
3
2) tan 210
11
3) csc
4


 

31. Utilizando Identidades
Trigonométricas
1
1) Sea un ángulo en el Cuadrante II tal que sin .
3
Encuentra cos y tan .
5
2) Sea un ángulo en el Cuadrante IV tal que csc .
8
Encuentra sec y cot .
 
 
 
 



32. π/2 π 3π/2 2π
-1
-0.5
0.5
1
x
y
Gráficas de las Funciones Seno y
Coseno
  sinf x x
Periodo: 2π

33. Gráficas de las Funciones Seno y
Coseno
π/2 π 3π/2 2π
-1
-0.5
0.5
1
x
y
  cosf x x
Periodo: 2π

34. Amplitud y Periodo de las Curvas de
Seno y Coseno
 siny a bx c d  
 cosy a bx c d  

35. Amplitud y Periodo de las Curvas de
Seno y Coseno
La amplitud de
sin y cos
representa la mitad de la distancia entre los valores
máximos y mínimos de la función y está dada por
Amplitud .
y a x y a x
a
 

π/2 π 3π/2 2π
-2
-1.5
-1
-0.5
0.5
1
1.5
2
x
y
2si
s
1
n
i
i
n
s
2
ny x
y x
y x




36. Amplitud y Periodo de las Curvas de
Seno y Coseno
La amplitud de
sin y cos
representa la mitad de la distancia entre los valores
máximos y mínimos de la función y está dada por
Amplitud .
y a x y a x
a
 

π/2 π 3π/2 2π
-2
-1.5
-1
-0.5
0.5
1
1.5
2
x
y
2si
s
1
n
i
i
n
s
2
ny x
y x
y x




37. Amplitud y Periodo de las Curvas de
Seno y Coseno
La amplitud de
sin y cos
representa la mitad de la distancia entre los valores
máximos y mínimos de la función y está dada por
Amplitud .
y a x y a x
a
 

π/2 π 3π/2 2π
-2
-1.5
-1
-0.5
0.5
1
1.5
2
x
y
2si
s
1
n
i
i
n
s
2
ny x
y x
y x




38. Amplitud y Periodo de las Curvas de
Seno y Coseno
Sea un número positivo real. El periodo de sin
y cos está dado por
2
Periodo .
b y a bx
y a bx
b




π/2 π 3π/2 2π 5π/2 3π 7π/2 4π
-1
-0.5
0.5
1
x
y
sin 2
n
2
i
n
s
si
y x
y
y x
x




39. Amplitud y Periodo de las Curvas de
Seno y Coseno
Sea un número positivo real. El periodo de sin
y cos está dado por
2
Periodo .
b y a bx
y a bx
b




π/2 π 3π/2 2π 5π/2 3π 7π/2 4π
-1
-0.5
0.5
1
x
y
sin 2
n
2
i
n
s
si
y x
y
y x
x




40. Amplitud y Periodo de las Curvas de
Seno y Coseno
Sea un número positivo real. El periodo de sin
y cos está dado por
2
Periodo .
b y a bx
y a bx
b




π/2 π 3π/2 2π 5π/2 3π 7π/2 4π
-1
-0.5
0.5
1
x
y
sin 2
n
2
i
n
s
si
y x
y
y x
x




41. Translaciones de las Curvas Seno y
Coseno
   Las gráficas de sin y cos
tienen las siguientes características. (Asume que 0)
2
Amplitud Periodo
Los extremos izquierdos y derechos de un intérvalo de
un ciclo pueden ser de
y a bx c y a bx c
b
a
b

   

 
terminados resolviendo las
ecuaciones 0 y 2 .bx c bx c    

42. Translaciones de las Curvas Seno y
Coseno
 
1
Analiza la gráfica de sin .
2 3
Analiza la gráfica de 3cos 2 4 .
y x
y x

 
 
  
 
  

43. Translaciones de las Curvas Seno y
Coseno
   
Una translación vertical es causada por la constante
en las ecuaciones
sin y cos
La translación es unidades hacia arriba si 0
y unidades hacia abajo si 0.
d
y a bx c d y a bx c d
d d
d d
     


Analiza la gráfica de 3cos2 2y x 

44. Encontrando la Ecuación para una
Gráfica
• Encuentra la amplitud, periodo y cambio de fase
de la función seno, cuya gráfica se presenta.
Escribe una ecuación para esta gráfica.
-π/2 π/2 π 3π/2
-2
-1
1
2
x
y

45. Funciones Trigonométricas Inversas
   
La función seno inverso esta definida por
arcsin si y solamente si sin
donde 1 1 y 2 2. El dominio
de arcsin es 1,1 y el alcance es 2, 2 .
y x y x
x y
y x
 
 
 
     
  

46. Funciones Trigonométricas Inversas
1
1
Si es posible, encuentra el valor exacto.
1
a. arcsin
2
3
b. sin
2
c. sin 2


 
 
 

47. Funciones Trigonométricas Inversas
Función Dominio Alcance
arcsiny x si y solamente si sin y x 1 1x  
2 2
y
 
  
arccosy x si y solamente si cos y x 1 1x   0 y  
arctany x si y solamente si tan y x x   
2 2
y
 
  

48. Funciones Trigonométricas Inversas
 
 
1
1
Encuentra el valor exacto.
2
a. arccos
2
b. cos 1
c. arctan 0
d. tan 1



