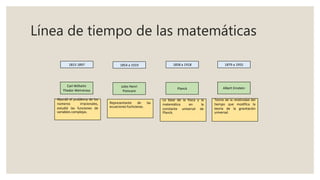
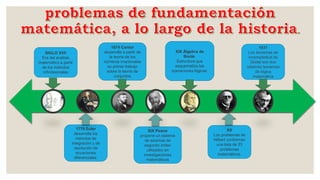
El documento presenta una línea de tiempo que resume los principales hitos en la historia de los fundamentos de las matemáticas, desde las primeras civilizaciones hasta el siglo XX. Incluye importantes contribuciones de matemáticos griegos como Pitágoras, Euclides y Arquímedes, así como el desarrollo del álgebra, el cálculo y la geometría analítica en los siglos posteriores. Finalmente, explica brevemente la "crisis de los fundamentos" que llevó a una investigación sistemática de los fundamentos matemá

1. Paso 4 - Realizar transferencia
del conocimiento
• ANGEL DANIEL CHAZATAR RAMIREZ
• CAROLINA OSORIO
• DARLING VIVIANA LUCENA
• DAVID BRAND
• ISABEL DEL ROSARIO CUAICAL
• 551103_10
• TUTOR: ANDRES FERNANDO MOSQUERA DIAZ

2. Introducción
◦ En la presentación siguiente tratan temas como problemas de
la fundamentación matemática, rigor de las matemáticas,
crisis de los fundamentos, y se presenta una línea de tiempo
donde se presenta los problemas de la fundamentación
matemática a lo largo de la historia ya también se presenta
un breve recuento de las matemáticas a través de la historia
mundial.

3. Objetivos
Generales
◦ Apreciar la aparición de las matemáticas y
de los problemas de fundamentación
matemática
◦ Ubicar en la línea de tiempo los principales
factores de la fundamentación matemática
Específicos
◦ Identificar las causas de la fundamentación
matemática.
◦ Interiorizar la rigorizacion matemática.
◦ Aprender y ubicar los momentos mas
significativos de la matemáticas en su
historia

4. problemas de
fundamentación matemática,
a lo largo de la historia.

5. Fundamentos de las
matemáticas
Los fundamentos de las matemáticas son el
estudio de conceptos matemáticos básicos como
números, figuras geométricas, conjuntos,
funciones, etc. y cómo forman jerarquías de
estructuras y conceptos más complejos,
especialmente las estructuras fundamentalmente
importantes que forman el lenguaje de las
matemáticas: fórmulas, teorías y sus modelos,
dando un significado a las fórmulas, definiciones,
pruebas, algoritmos, etc.

6. Los fundamentos de la matemática
griega
Aunque que el uso práctico de la matemática fue desarrollada ya en
civilizaciones de la edad de bronce, el interés específico por sus
aspectos fundacionales y teóricos parece remontarse a la matemática
helénica. Los primeros filósofos griegos discutieron ampliamente sobre
qué rama de la matemática era más antigua, si la aritmética o la
geometría. Zenón de Elea (490 a. C - ca. 430 a. C.) formuló cuatro
aporías que aparentan mostrar que el cambio es imposible, que en
esencia no fueron convenientemente aclaradas hasta el desarrollo de
matemática moderna.
La escuela pitagórica de matemática insistía originalmente en que solo
existían los números naturales y racionales. El descubrimiento de la
irracionalidad de √2, la proporción de la diagonal de un cuadrado con su
lado (data del siglo V a.C), fue un golpe filosófico a dicha escuela que
solo aceptaron de mala gana. La discrepancia entre racionales y reales
fue finalmente resuelta por Eudoxo de Cnido, un estudiante de Platón,
quien redujo la comparación de las proporciones de los irracionales a
comparaciones de múltiples proporciones racionales, además de
anticipar la definición de número real de Richard Dedekind.

7. Los fundamentos de la matemática
En el siglo IX, algunos árabes como Al-Juarismi se interesan por la matemática y reúnen los saberes
griegos e indios, mientras que en Occidente se dejan de lado. La introducción del sistema de
numeración arábigo en el siglo XI marca el fin de un periodo en el que las matemáticas fueron
prácticamente olvidadas, por culpa de las grandes invasiones y del dogmatismo, que mantenía las
conciencias en el oscurantismo.
Los fundamento mas destacados de este periodo:
• Los logaritmos neperianos (1614): el logaritmo neperiano de unos textos x es el exponente a al
que debe ser elevado el número e para obtener x. También se les llama logaritmos hiperbólicos
porque representan el área de la hipérbole entre dos asíntotas.
• La geometría analítica de René Descartes: en su obra La geometría, propone unir álgebra y
geométrica (como Viète); traduce así las cuestiones geométricas en ecuaciones algebraicas.
Recordemos que uno de los objetivos principales de Descartes, independientemente del tema, es
obtener ideas claras.
• El cálculo de probabilidades de Blaise Pascal: se trata de calcular las posibilidades de que algo
suceda debido al azar. El análisis de los juegos de azar fue el punto de partida.
• Los inicios del calcular infinitesimal de Newton.

8. EL RIGOR EN LAS MATEMÁTICAS
Durante el siglo XIX, se dio un proceso de rigorización que buscaba
esclarecer algunos conceptos y definirlos de una mejor manera. Por
ejemplo, las nociones de función, derivada, continuidad, integral.
También se buscaba dar un tratamiento más consistente a las series,
puesto que durante el siglo XVIII no se ponía mucho cuidado de si
estas eran convergentes o divergentes; de hecho, se llegaba a
contradicciones importantes. Uno de los ejemplos son las
representaciones de las funciones por medio de series
trigonométricas, que habían incurrido en algunas confusiones.
Este proceso de establecer un mayor rigor en los conceptos y
métodos del Cálculo va a introducirse en la historia de las
matemáticas del siglo XIX dentro de un período en el que se
desarrollaron nuevas geometrías y se potenció la abstracción en el
álgebra. Puede decirse que sería un período en el que iban a perder
su asidero propiedades tan importantes de los sistemas numéricos
conocidos como la conmutatividad, o una geometría que daba cuenta
de manera natural de representar nuestras percepciones de la
realidad exterior, la euclidiana, y también se iba a expandir un nuevo
carácter de las matemáticas.

9. Crisis de los fundamentos
La crisis fundacional de la matemática (llamada originalmente en
alemán: Grundlagenkrise der Mathematik) fue un término acuñado
a principios del siglo xx para referirse a la situación teórica que llevó
a una investigación sistemática y profunda de los fundamentos, que
acabó inaugurando una nueva rama de la matemática.
Numerosas escuelas filosóficas matemáticas incurrieron en
dificultades una tras otra, a medida que la asunción de que los
fundamentos de la matemática podían ser justificados de manera
consistentes dentro de la propia matemática fue puesta en duda por
el descubrimiento de varias paradojas (entre ellas la célebre
paradoja de Russell).
El término "paradoja" no debe ser confundido con el término
contradicción. Una contradicción dentro de una teoría formal es una
demostración formal de la existencia de un absurdo como resultado
de un conjunto de asunciones inapropiadas (tales como 2 + 2 = 5),
un conjunto de axiomas o teoría que da lugar a una contradicción
se clasifica de inconsistente y debe ser rechazada como teoría útil
(ya que en ella cualquier proposición acabaría siendo demostrable).

10. 25.000 a 5.000 a.c
Medir y contar fueron las
primeras actividades del
hombre primitivo. Haciendo
marcas en los troncos de
árboles lograron la medición
del tiempo y el número de
animales.
5.000 a 500 a.c
Encontramos los primeros
vestigios de una ciencia
matemática.
Algebra en el
antiguo Egipto
5.000 a 500 a.c
Asirios y Babilónicos
contribuyeron al acervo
matemático.
Cálculo en Caldea
y Asirio
640 a 535 a.c
El primero y más famoso
de los 7 sabios de Grecia.
Predijo el eclipse
de sol en 1585
585 a 500 a.c
Aportó conceptos
fundamentales a la
matemática.
Pitágoras
429 a 343 a.c
Filósofo matemático que
alcanzó el pleno dominio
de la ciencia en su tiempo.
Platón
365 al 275 a.c
Matemático griego
estableció un método
riguroso de demostración
geométrica.
Euclídes
287 al 212 a.c
Fue el primero en aplicar
metódicamente las ciencias
a los problemas de la vida
real.
Arquímedes
Línea de tiempo de las matemáticas

11. Línea de tiempo de las matemáticas
100 a 175 d.c
El más sobresaliente de la
era Helenística
Plotomeo
375 a 415 d.c
Siguió los lineamientos de
Platón y Aristóteles siendo
uno de los últimos
matemáticos griegos.
Ipatía
Siglo V, VI, VII d.c
Tres nombres se pueden
señalar como hitos en la
historia de la matemática
India: Aryabhta,
Braomaguptoa, Bhaskara.
Algebristas de la
India
Siglos XIX al XII
Pertenecían Al eJuarismi,
Al Batani y Omar Khayyan.
Escuela de Bagdad
Siglo VII al XV
Tres nombres pueden
señalarse como
representantes: Geber Ibn-
Aphia, Arsaquel, Benerza.
Matemáticas en
Universidades
Hispano árabes
Siglo VII
La matemática
hispanoárabe se introduce
a Europa a través de las
traducciones de estos
eruditos.
Programadores
Europeos de la
matemática
1175 a 1250
Da a conocer en occidente
los métodos matemáticos
Indues
Leonardo de Pisa
1499 a 1557
Sostuvo una polémica con
cardano sobre quien fue el
primero en descubrir la
solución de la ecuación
cubica y cuadrática.
Nicolas de
Tartaglia

12. Línea de tiempo de las matemáticas
1501 - 1576
Le atribuyen haber
arrebatado Tartalia la
fórmula para resolver las
ecuaciones cúbicas y
cuadráticas.
Jerónimo Cardano
1540 a 1603
Se considera el fundador
del algebra mderna
Foncoise Viete
1596 a 1650
Es el que sistematiza el
método científico. Aplica el
álgebra a la geometría
analítica.
Renato Descartes
1601 a 1665
Profundiza los maravillosos
y extraordinarios caminos
de la matemática pura.
Pierre Fermat
1623 a 1662
Demostró las 32
preposiciones de Euclídes,
Pascal cimienta las bases
de la teoría de la
probabilidad.
Blase Pascal
1642 - 1727
Descubrió cálculo
diferencial y cálculo
integral. Formuló la ley de
gravitación universal.
Isaac Newton
1646 a 1716
Descubre simultáneamente
con Newton el cálculo
diferencial. Desarrollo
notablemente el análisis
combinatorio.
Gottfried Wigelant
Leibnitze
1685 a 1731
Método de los incrementos
directos e inversos. En el
álgebra elemental
conocemos el teorema de
Taylor.
Brook Taylor

13. Línea de tiempo de las matemáticas
1707 a 1783
Considerado el fundador
de la ciencia moderna.
Leonard Euler
1717 a 1783
Concibió y realizó con
Dierot la idea de la
enciclopedia. Redactó
todos los artículos
matemáticos.
Leront Dalembert
1736 a 1813
Escribió “sobre la
resolución de las
ecuaciones numéricas”.
José Luis Lagranje
1746 a 1818
Inventó la geometría
descriptiva.
Gaspar Monje
1749 a 1827
Creó la teoría sobre el
origen del sistema solar.
Pierre Simon
Laplace
1777 a 1855
Demostró primero que
nadie el llamado Teorema
fundamental del Algebra.
Carl Friederich
Gauss
1793 a 1856
Se considera el precursos
de la relatividad y de las
geometrías no Euclidianas
Nicolas
Loratchewski
1804 a 1851
Fue el primero en aplicar
estas funciones elípticas a
la teoría de los números
Karl Gustav Jacobi

14. Línea de tiempo de las matemáticas
1815 1897
Abordó el problema de los
números irracionales,
estudió las funciones de
variables complejas.
Carl Wilhelm
Thedor Weirstrass
1854 a 1919
Representante de las
ecuaciones fuchsianas.
Jules Henri
Poincare
1858 a 1918
La base de la física y la
matemática en la
constante universal de
Planck.
Planck
1879 a 1955
Teoría de la relatividad del
tiempo que modifica la
teoría de la gravitación
universal.
Albert Einstein

15. SIGLO XVII
Era del análisis
matemático a partir
de los métodos
infinitesimales
XX
Los problemas de
Hilbert conforman
una lista de 23
problemas
matemáticos
XIX Peano
propone un sistema
de axiomas de
segundo orden
utilizados en
investigaciones
matemáticas
1770 Euler
desarrolla los
métodos de
integración y de
resolución de
ecuaciones
diferenciales
1874 Cantor
desarrolla a partir de
la teoría de los
números irracionales
su primer trabajo
sobre la teoría de
conjuntos
XIX Álgebra de
Boole.
Estructura que
esquematiza las
operaciones lógicas
1931
Los teoremas de
incompletitud de
Gödel son dos
célebres teoremas
de lógica
matemática

16. bibliografía
• Ortiz Fernández, A. (1988). Crisis en los fundamentos de la matemática. Pro
Mathematica, 2(3), 31-47.
http://revistas.pucp.edu.pe/index.php/promathematica/article/view/6053
• Gómez, R. & Recalde, L. (2013). Epistemología de las matemáticas. Modulo.
Universidad Nacional Abierta y a Distancia. http://hdl.handle.net/10596/10981
• Bell, E. T. (1985). Historia de las matemáticas. FCE - Fondo de Cultura Económica.
https://elibro-net.bibliotecavirtual.unad.edu.co/es/lc/unad/titulos/109496