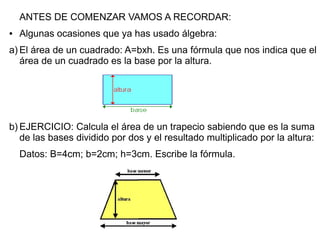
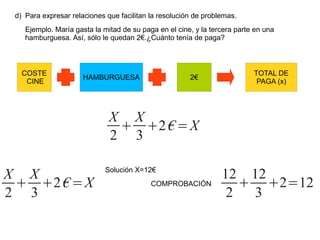
1) El álgebra estudia las estructuras, relaciones y cantidades mediante el uso de símbolos en lugar de números. Esto permite formular leyes de la aritmética de forma general y referirse a números desconocidos. 2) Las fórmulas son expresiones algebraicas que unen varias variables. El álgebra se usa para crear fórmulas que relacionan diferentes magnitudes. 3) Se utilizan ejemplos como el cálculo del área de figuras, la propiedad distributiva y series numéricas para ilustrar cómo el álgebra facilit

1. MATEMÁTICAS
2ºESO
ÁLGEBRA
Javier García

2. El álgebra es la rama de las matemáticas que estudia las
estructuras, las relaciones y las cantidades.
En álgebra los números son representados por símbolos
(usualmente a, b, c, x, y, z). Esto es útil porque:
● Permite la formulación general de leyes de aritmética (como a
+ b = b + a).
● Permite referirse a números "desconocidos", formular
ecuaciones y el estudio de cómo resolverlas.
LAS FÓRMULAS SON EXPRESIONES ALGEBRÁICAS QUE
UNEN VARIAS VARIABLES.

3. ANTES DE COMENZAR VAMOS A RECORDAR:
● Algunas ocasiones que ya has usado álgebra:
a) El área de un cuadrado: A=bxh. Es una fórmula que nos indica que el
área de un cuadrado es la base por la altura.
b) EJERCICIO: Calcula el área de un trapecio sabiendo que es la suma
de las bases dividido por dos y el resultado multiplicado por la altura:
Datos: B=4cm; b=2cm; h=3cm. Escribe la fórmula.

4. c) La propiedad distributiva del producto respecto a la suma (ya lo vimos
anteriormente) y escribíamos:
a·(b+c)=a·b+a·c
d) EJERCICIO:
Completa:
5·(6+8)=5·___+5·___
30+24=6·___+6·___ =6·(__+__)=6·__
e) Cómo se suprimen los paréntesis precedidos de signos + o -
+(a+b-c)=+a+b-c
-(a+b-c)=-a-b+c
f) EJERCICIO:
I. Calcula de dos formas, quitando y sin quitar paréntesis:
a) 8-(9-5+2)
b) 3-(2+3-11)
II. Simplifica: a-(a+b)-b a+(a-b)-b

5. 1.- El álgebra. ¿Para qué sirve?
a) Para expresar propiedades de las operaciones aritméticas, por ejemplo la propiedad
distributiva (visto antes)
b) Para generalizar la evolución de series, ej: an=(n-1)·n
Por ejemplo en esa ecuación tendremos la siguiente serie de números: 0,2,6,12,20
0=(1-1)·1 (n=1, primera posición) ; 2=(2-1)·2 (n=2, Segunda posición)
6=(3-1)·3 (n=3, tercera posición) ; 12=(4-1)·4 (n=4, Cuarta posición)
c) Para expresar la relación entre variables relativas a distintas magnitudes (es decir
crear fórmulas): Ej
En un concesionario quieren calcular lo que tengo que pagar al mes para comprarme una moto, si puedo
dar una entrada de 500€ y quiero pagarla en 30 meses
X es el precio de la moto.
500€ es lo que pago de entrada El precio de lo que pague variará en función
de lo que valga la moto.
30 es el número de meses en los que la pagaré
Y será lo que pague al mes X −500
Y=
30

6. d) Para expresar relaciones que facilitan la resolución de problemas.
Ejemplo. María gasta la mitad de su paga en el cine, y la tercera parte en una
hamburguesa. Así, sólo le quedan 2€.¿Cuánto tenía de paga?
COSTE TOTAL DE
HAMBURGUESA 2€
CINE PAGA (x)
X X
 2 € = X
2 3
X X Solución X=12€
12 12
 2 € = X COMPROBACIÓN  2=12
2 3 2 3

7. EJERCICIOS

8. EXPRESIONES ALGEBRÁICAS
VAMOS A VER:
● Monomios. Es una expresión formada por un
valor conocido y uno o varios desconocidos,
representados por letras.
3· a 3 es el coeficiente y a la Parte Literal
3
· x · y 2 (3/5) es el coeficiente y x e y la parte literal
5
● Polinomios. Suma o resta de varios monomios
(si solo fueran dos, sería binomio, si son tres,
trinomio...)
x+ y 2 2
Binomios 3x +2x −1 Trinomio
2 2 3 2
a −1 3x −3x +2x −1 Polinomio

9. MONOMIOS
Un monomio es una expresión algebraica en la
que las únicas operaciones que aparecen entre
las variables son el producto y la potencia de
exponente natural.
Partes de un monomio
● Coeficiente: El coeficiente del monomio es el número que aparece
multiplicando a las variables.
● Parte literal: La parte literal está constituida por las letras y sus exponentes
4· a 3 es el coeficiente y a la Parte Literal
1 3
· y · x (1/4) es el coeficiente y x e y la parte literal
4
1
· y · x +3x · y No es un monomio porque aparece una suma y SÓLO PUEDE HABER
3
4 PRODUCTO O POTENCIA