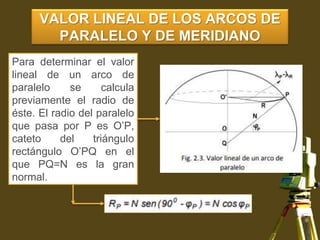
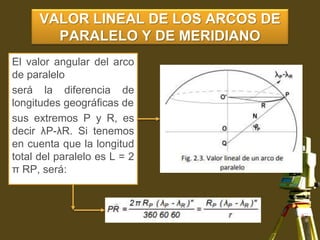
Este documento proporciona información sobre sistemas de referencia geodésicos. Explica que los sistemas de referencia definen un marco de coordenadas para situar puntos en la Tierra y son importantes para la cartografía, topografía y navegación. También describe los componentes clave de los sistemas de referencia como el elipsoide de referencia, el marco de referencia físico y los sistemas de coordenadas asociados. Finalmente, resume los parámetros del elipsoide de referencia del sistema WGS84, actualmente el más

1. CURSO
GEODESIA
DOCENTE:
ING. JORGE SÁNCHEZ

2. CONTENIDO
• Elipsoide de referencia
• Excentricidad, definiciones

3. INTRODUCCIÓN
Los Sistemas de referencia en principio no parecen
tener mucha relación con el Catastro y sí con la
Geodesia.
Pero si abrimos cualquier pliego de Prescripciones
Técnicas de la Dirección General de Catastro,
Urbana o Rústica, veremos que la mayoría de ellos
empiezan definiendo el Sistema de Referencia y El
Sistema Geodésico. Estos nos van a definir los
distintos juegos de coordenadas
con las que vamos a asignar las Referencias
Catastrales.
Este artículo es un monográfico sobre los Sistemas
de referencia y su evolución a lo largo de la historia,
en función de los métodos de observación y la
precisión utilizada para su definición.

4. Será necesario un sistema de referencia terrestre para la
determinación de coordenadas sobre la Tierra, de
manera que se convierte en una herramienta
imprescindible en el desarrollo de la Cartografía, la
Topografía, la Navegación sobre la superficie terrestre y
para la localización de cualquier observación que se
realice.

5. Sistema de
Referencia
Referencia
espacial
Referencia
terrestre

6. Sistema de
Referencia
• Son teorías, hipótesis y constantes que permiten situar una
tripleta de ejes coordenados en el espacio, definiendo su
origen y su orientación.
Marco de
Referencia
• Es la materialización de un sistema de referencia convencional
a través de observaciones, es decir, se trata de un conjunto de
puntos con coordenadas y velocidades conocidas en ese
sistema de referencia convencional y materializan el espacio el
sistema de referencia.
Sistema de
Coordenadas
• Es la parametrización de las coordenadas de los puntos que
forman el marco de referencia. Existen infinitos sistema de
coordenadas para parametrizar el marco de referencia.

7. Se pueden haber emitido certificaciones catastrales e incluso se
pueden haber inscrito las propiedades en el Registro de la
Propiedad, con la inclusión de esta referencia catastral, y si se
cambiara, acarrearía problemas a los interesados.
Los distintos países, por acuerdo, pueden en un determinado
momento definir un Sistema de Referencia más preciso Inercial.
Ejemplo: WGS-84 por necesidades en la navegación marítima y
aérea.
Se pueden transformar las coordenadas de un Sistema de
Referencia a otro a través de operaciones matemáticas.
La referencia catastral, por tanto, variaría de un sistema de
referencia a otro, o en un mismo sistema si es inercial.

8. SISTEMAS DE REFERENCIA INERCIALES
• Apropiados para definir la situación, el
movimiento de objetos externos a la tierra, como
estrellas, planetas, satélites, etc.
• Permiten efectuar cálculos empleando la fórmula
Newtoniana.
• Recibe el nombre de sistemas no inerciales.
• Se pueden relacionar al campo gravitatorio.

9. SISTEMAS DE REFERENCIA TERRESTRES
• La materialización física de los sistemas de referencia se
establece dando coordenadas a una serie de puntos
convenientemente monumentados, que constituyen el
marco de referencia.
• De ésta forma, el marco de referencia para un topógrafo
sería la red geodésica, formada por los vértices
geodésicos y las coordenadas asociadas a los mismos.
Las variaciones de dirección que experimentan los ejes de los
sistemas de referencia terrestres respecto al espacio, lo que
produce una variación de las coordenadas absolutas de los
vértices geodésicos.
Los desplazamientos y deformaciones que experimenta la
corteza terrestre, a la que están sujetos los vértices
geodésicos y que producen variaciones relativas de
coordenadas.

10. SISTEMA DE REFERENCIA
TERRESTRE CONVENCIONAL (CTRS)
Exigencias de precisión en un sistema de
referencia geodésico.
El sistema de referencia elipsoidal con modelo de Tierra
rígida puede considerarse válido para una precisión de
hasta 10*-6.
Podrá ser utilizado, por tanto siempre que efectuemos
mediciones con una precisión relativa igual o menor.

11. MOVIMIENTO DEL POLO CON
MODELO DE TIERRA DEFORMABLE
Considerar un
modelo de Tierra
elástico o
deformable supone
tener en cuenta la
variación en el
tiempo de la
distribución de
masas.

12. RADIOS DE CURVATURA DEL ELIPSOIDE
En un punto dado P estos
radios de curvatura son los de
las dos secciones del
elipsoide, perpendiculares
entre sí, que tienen
curvaturas mínima y máxima,
respectivamente.
Los radios de curvatura de
todas las restantes secciones
posibles, trazadas por P,
adoptarán valores
intermedios entre esos dos.

13. Cuando el arco tiende a cero, el punto
intersección tendrá un límite denominado centro
de curvatura de la elipse meridiana. El valor del
radio de curvatura en P depende de la latitud
geográfica del punto P y se calcula:
Donde: e la primera excentricidad y φ la latitud del punto
Los radios de curvatura principales son iguales
en los polos y en el Ecuador.
Se denomina esfera local a la que tiene más
puntos de contacto con la superficie del
elipsoide en torno a P. Su radio es la media
geométrica entre los de la gran normal y la
elipse meridiana en P.

14. VALOR LINEAL DE LOS ARCOS DE
PARALELO Y DE MERIDIANO
Para determinar el valor
lineal de un arco de
paralelo se calcula
previamente el radio de
éste. El radio del paralelo
que pasa por P es O’P,
cateto del triángulo
rectángulo O’PQ en el
que PQ=N es la gran
normal.

15. VALOR LINEAL DE LOS ARCOS DE
PARALELO Y DE MERIDIANO
El valor angular del arco
de paralelo
será la diferencia de
longitudes geográficas de
sus extremos P y R, es
decir λP-λR. Si tenemos
en cuenta que la longitud
total del paralelo es L = 2
π RP, será:

16. CORRECIONES PARA REDUCIR AL
ELIPSOIDE LAS DISTANCIAS MEDIDAS
Las mediciones de ángulos y distancias se realizan
sobre el terreno. En casos en que se requiera gran
precisión, o bajo determinadas circunstancias
especiales, será preciso reducirlas al elipsoide. La
reducción para las medidas angulares es insignificante,
incluso en distancias grandes (25‐30km), por lo que
prescindiremos de ella.
Para las distancias, la reducción al elipsoide suele
hacerse en tres etapas, que se desarrollan a
continuación. Si la medición va a realizarse por
métodos electrónicos, que es el procedimiento normal,
es importante que antes de medir se hayan introducido
todas las correcciones propias de este sistema y,
especialmente, la corrección atmosférica

17. REDUCCIÓN AL HORIZONTE MEDIO
Una distancia natural D medida entre dos
puntos de diferente altitud A y B. Esta
corrección permite obtener la distancia
reducida D1 a una altitud media entre las de
los dos puntos:
Siendo Δh la diferencia de altitud:
La corrección c siempre tendrá un valor negativo.
La distancia reducida al horizonte medio será:

18. REDUCCIÓN AL NIVEL DEL MAR
De forma aproximada, la distancia reducida al
nivel del mar puede calcularse mediante la
expresión.
Como radio RL es suficiente con tomar el
de la esfera local en un punto de latitud
intermedia entre las de A y B. hm es la
altitud media entre los dos Puntos.

19. PASO DE LA CUERDA AL ARCO
Esta última etapa consiste en calcular la
distancia geodésica, es decir, en pasar de la
cuerda D2 que hemos obtenido en la etapa
anterior al arco de elipsoide D3 entre los
puntos A y B.
La expresión a aplicar es:

20. Al CTRS se le suele asociar un elipsoide de referencia. En
la actualidad, entre los más Empleados, se encuentran el
elipsoide de Hayford y el asociado al WGS-84. Sus
parámetros geométricos se muestran a continuación:
El CTRS equivaldría a un sistema elipsoidal con
modelo de Tierra rígida. La diferencia estriba en
que el movimiento del CTP respecto al CEP es
conocido. Es decir, que en cualquier momento se
pueden relacionar las coordenadas obtenidas en
una determinada época con las de otra.

21. Los Sistemas de Referencia no
son invariantes puesto que se
aplican a la Tierra, que es un
sólido no rígido, que tiene o
presenta variaciones en su centro
de gravedad, en su polo, en su
velocidad de rotación, incluso en
su conformación interna y
externa.
Las coordenadas dentro de un
mismo sistema son únicas e
invariantes para un mismo punto,
luego la referencia es única para
cada parcela dentro de un mismo
sistema de referencia. Las
coordenadas se pueden
replantear en cualquier momento
a partir de los vértices
Geodésicos.

22. Sistemas de referencia geodésicos
globales y WGS84
Geodetic Reference
System 1980 (GRS80)
World Geodetic
System 1984 (WGS84)
Este sistema reemplaza al
GRS67 por no representar
adecuadamente el
tamaño, forma y el campo
gravitatorio con precisión
suficiente para la mayoría
de aplicaciones
geodésicas, geofísicas,
astronómicas e
hidrográficas.
Utilizado por la técnica
GPS y obtenido
exclusivamente a partir de
los datos de la
constelación de satélites
GPS.

23. MARCO DE REFERENCIA
WGS84
Actualmente existe un nuevo refinamiento,
WGS84(G1150), ya que las estaciones de
referencia han aumentado de 5 a 16: 10 de la
fuerza aérea Norteamericana y 6 de la NIMA;
después de alinear esta actualización al marco
ITRF2000, fijando para el cálculo de las
coordenadas WGS84 49 estaciones
ITRF, las diferencias entre WGS84(G1150) e
ITRF2000 indican que se trata de marcos
virtualmente idénticos.

25. Se define el siguiente modo:
• Origen, centro de masas de la Tierra
incluyendo océanos y atmósferas.
• Eje Z paralelo a la dirección del polo CIO o
polo medio definido por el BIH, época 1984 con
una precisión de 0.005”.
• Eje X, la intersección del meridiano origen,
Greenwich y el plano que pasa por el origen
perpendicular al eje Z.
• El eje Y ortogonal a los anteriores, pasando por
el origen.

26. Este sistema de referencia está asociado al
elipsoide definido por los siguientes parámetros:
Semejanza mayor de la elipse a = 6 378.137 km
Semieje menor de la elipse b = 6 356.752 km
Factor de achatamiento f = 1/298, 257223563

27. CÁLCULOS GEODÉSICOS
Sea a el semieje mayor de la elipse meridiana y b el
semieje menor. A partir de sus valores se obtienen los
siguientes parámetros de la elipse:
Aplanamiento o achatamiento
Primera excentricidad
Segunda excentricidad
Excentricidad lineal