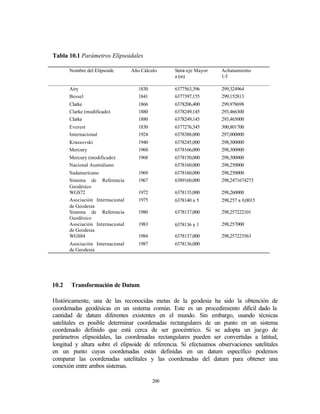
Este documento presenta un prefacio y una tabla de contenido para un texto sobre geodesia geométrica. El prefacio explica que el texto traduce y complementa una serie de lecciones sobre propiedades del elipsoide y curvas en su superficie. La tabla de contenido lista 10 capítulos que cubren temas como propiedades del elipsoide, curvas en la superficie del elipsoide, solución de triángulos elipsoidales y cálculo de coordenadas geodésicas.

1. GEODESIA GEOMÉTRICA
PARTE I
Escrito en Inglés por Richard H. Rapp
(Abril de 1991)
Revisado y Traducido al Español por Oscar A. Cifuentes
oscifuen@udec.cl
(Enero de 2001)
INSTITUTO GEOGRAFICO MILITAR
Observatorio Geodésico Integrado Transportable
TIGO
Concepción - Chile
Julio de 2001

2. PREFACIO
A partir del siglo XVIII, la forma precisa de la Tierra fue reconocida como un
elipsoide de revolución; desde entonces, el posicionamiento geodésico sobre la
superficie de la Tierra ha venido efectuándose mediante mediciones que son
idealmente reducidas a un elipsoide para análisis adicional a través de los ajustes
de datos. Por ello, es importante entender las propiedades básicas del elipsoide y
las curvas sobre su superficie, las cuales son pertinentes a los cálculos geodésicos.
La información aquí proporcionada es la base de un curso consistente en cuarenta
lecciones de geodesia geométrica, dictado en la Universidad Estatal de Ohio
(OSU), Estados Unidos de Norteamérica. En el desarrollo del curso no todo el
material puede ser cubierto, excepto citándolo como referencia.
El desarrollo de las herramientas matemáticas para el análisis de la geometría del
elipsoide con propósitos geodésicos ha sido utilizado durante varios siglos. Estos
apuntes toman ventaja de las derivaciones previas del material. Aunque uno podría
pensar que todo lo que se necesita ya ha sido derivado, es una idea falsa. Hoy día,
nuevas técnicas continúan publicándose para mejorar eficientemente los cálculos y
la precisión. Tales antecedentes han sido incluidos en el texto, cuando es
apropiado.
Estas notas son una traducción del texto Geometric Geodesy, Part I, desarrollado
por el profesor Dr. Richard H. Rapp en sus clases en la OSU, desde 1975. La
Escuela Cartográfica de Defensa del Servicio Geodésico Interamericano tiene una
traducción al Español del texto original fechada en junio de 1988. No obstante, la
obtención de una copia de ese material al finalizar la presente versión, se entrega
para dominio público esta nueva edición. El profesor Rapp ha consentido la
publicación de esta nueva versión en la página web del Instituto Geográfico
Militar.
En esta traducción se ha complementado el texto con definiciones, notas y
algoritmos que contribuyen a llenar un vacío que existía en esta materia. El
propósito para efectuar este trabajo no es otro que poner al alcance de los
estudiantes hispanos en geomensura, geociencias en general y especialidades
relacionadas, el material que el traductor recopiló durante sus estudios de
postgrado en ciencias de la geodesia desarrollados en la OSU.
El traductor agradece al profesor R. H. Rapp la gentileza de permitir esta
publicación y al profesor Kennet Brace del National Imagery and Maping Agency
por enviar una copia de la versión traducida en Junio de 1988. También se
agradece a la Señorita Lucía Álvarez G. del Instituto Geográfico Militar, quién
llevó al computador gran parte del texto y fórmulas.
ii

3. TABLA DE CONTENIDO
1. INTRODUCCIÓN
1.1 Definiciones 1
1.2 Geodesia y Otras Disciplinas 2
1.3 Bases Teóricas de la Geodesia 3
1.4 Historia de la Geodesia 3
2. PROCEDIMIENTOS MATEMÁTICOS ÚTILES
2.1 Series de Taylor y Maclaurin 9
2.2 Las Series Binomiales 10
2.3 Inversión de Series 11
2.4 Resumen de Expansiones Trigonométricas 13
2.5 Fórmulas de Ángulo Múltiple 13
3. PROPIEDADES DEL ELIPSOIDE
3.1 Introducción 17
3.2 Coordenadas Geodésicas 22
3.3 La Elipse Meridiana 23
3.4 Relaciones entre las Diferentes Latitudes 32
3.5 Radios de Curvatura del Elipsoide 35
3.5.1 Radio de Curvatura en el Meridiano 36
3.5.2 Radio de Curvatura en el Primer Vertical 41
3.5.3 Radio de Curvatura de la Sección Normal en el Acimut α 45
3.6 Extensión de un Arco de Meridiano 45
3.7 Extensión de un Arco de Paralelo 51
3.8 Cálculo de Áreas en la Superficie del Elipsoide 52
3.9 Radio de Aproximación Esférica de la Tierra ó Radio Medio de la
Tierra como si ésta fuese una Esfera 55
3.9.1 Radio Medio Gausiano 55
3.9.2 Radio de una Esfera que tiene el Promedio de los Tres Semiejes del
Elipsoide 56
iii

4. 3.9.3 Radio Esférico de la Esfera con igual Área que el Elipsoide 56
3.9.4 Radio de una Esfera con igual Volumen que el Elipsoide 57
3.10 Coordenadas Rectangulares Espaciales 58
3.11 Una Forma Alterna para la Ecuación del Elipsoide 60
4. CURVAS EN LA SUPERFICIE DEL ELIPSOIDE
4.1 Secciones Normales 63
4.1.1 Introducción 63
4.1.2 Separación entre Secciones Normales Recíprocas 66
4.1.3 Separación Lineal de Secciones Normales Recíprocas 71
4.1.4 Separación Acimutal de una Sección Normal Recíproca 74
4.1.5 El Arco Elíptico de una Sección Normal 76
4.1.6 Corrección del Acimut debido a la Altura del Punto Observado 78
4.1.7 El Ángulo de Declinación de la Cuerda 81
4.1.8 La Sección Normal y la Magnitud de la Cuerda 82
4.1.9 La Sección Normal en un Sistema de Coordenadas Local 84
4.2 La Curva Geodésica 88
4.2.1 Coordenadas Locales x, y, z en Términos de la Geodésica 96
4.2.2 Longitud de un Arco Diferencial de una Geodésica Rotada 99
4.2.3 Relación entre la Geodésica y la Longitud de la Cuerda 100
4.2.4 Comparación de la Geodésica con la Sección Normal 100
4.2.5 Diferencia de Longitud entre la Sección Normal y la Geodésica 104
4.3 El Gran Arco Elíptico y la Curva de Alineación 105
4.4 Reducción Geométrica de Observaciones de Dirección o Acimut 107
5. SOLUCIÓN DE TRIÁNGULOS ESFÉRICOS Y ELIPSOIDALES
5.1 Exceso Esférico 108
5.2 Solución del Triángulo Esférico por el Teorema de Legendre 109
5.3 Solución de Triángulos Esféricos por Aditamentos 115
iv

5. 6. CÁLCULO DE LAS COORDENADAS GEODÉSICAS (SOLUCIONES
DEL TRIÁNGULO POLAR ELIPSOIDAL)
6.1 Introducción 118
6.2 Desarrollo de Series en Potencias de s (Legendre) 119
6.2.1 El Problema Directo 119
6.2.2 La Solución Inversa 125
6.3 Las Fórmulas de Puissant 127
6.3.1 El Problema Directo 127
6.3.2 El Problema Inverso 134
6.4 Las Fórmulas de la Latitud Media de Gauss 135
6.5 Las Fórmulas de Bowring 140
6.6 El Método de la Cuerda 142
6.6.1 El Problema Inverso 142
6.6.2 El Problema Directo 142
6.7 Exactitud de los Métodos Directo e Inverso para Líneas de
Longitud Mediana 146
6.8 El Problema Inverso para las Coordenadas Rectangulares
Espaciales 148
7. INFORMACIÓN ASTROGEODÉSICA
7.1 Coordenadas Astronómicas 156
7.2 Comparación de Cantidades Angulares Astronómicas y
Geodésicas 159
7.2.1 Corrección de Dirección por Efecto de la Deflexión de la Vertical 168
7.2.2 Ecuación Extendida de Laplace 169
7.3 Ondulación Astrogeodésica del Geoide 170
7.4 Reducción de Distancias Medidas al Elipsoide 175
8. FÓRMULAS DIFERENCIALES DEL PRIMER Y SEGUNDO TIPO
8.1 Fórmulas Diferenciales del Primer Tipo 180
8.2 Fórmulas Diferenciales del Segundo Tipo 188
v

6. 9. ECUACIONES DE OBSERVACIÓN PARA TRIANGULACIÓN Y
TRILATERACIÓN CALCULADAS EN EL ELIPSOIDE
9.1 Relaciones Entre Distancias y Direcciones 192
9.2 Las Ecuaciones de Observación 195
9.3 La Ecuación de Observación de Acimut de Laplace 197
9.4 Formas de Ecuaciones de Observación Alternas 197
10. DATUM GEODÉSICO Y ELIPSOIDES DE REFERENCIA
10.1 Desarrollo de los Datums 199
10.2 Transformación de Datum 200
BIBLIOGRAFÍA 204
vi

7. LISTADO DE FIGURAS
1.1 Geometría de la Medición de Eratóstenes 4
1.2 La Forma de la Tierra según las Antiguas Mediciones Francesas 6
1.3 Elipse Achatada en los Polos 7
1.4 Relación entre Elipsoide, Terreno y Geoide 8
3.1 La Elipse Básica 17
3.2 Notación para la Elipse 18
3.3 Sistema de Coordenadas para el Elipsoide 22
3.4 Elipse Meridiana 23
3.5 Latitud Reducida 24
3.6 Latitud Geocéntrica 24
3.7 Interpretación Geométrica de W y V 29
3.8 Porción de un Arco de Meridiano 38
3.9 Radios de Curvatura de Meridianos Ecuatorial y Polar 40
3.10 Radio de Curvatura del Primer Vertical 41
3.11 Geometría para el uso del Teorema de Meusnier 42
3.12 Deducción Geométrica de N(A) 43
3.13 Deducción Geométrica de N(B) 44
3.14 Extensión del Arco de un Paralelo 51
3.15 Elemento de Área en el Elipsoide 52
3.16 Geometría de un Punto Localizado Fuera de una Elipse Meridiana 59
3.17 Sistema Local de Coordenadas en el Elipsoide 61
4.1 Determinación de la Distancia OnA 64
4.2 Un Triángulo de Sección Normal 65
4.3 Ángulo entre las Secciones Normales Recíprocas en la Cuerda que las
Conecta 66
4.4 Geometría de la Sección Normal 67
4.5 Una Aproximación Para el Arco Esférico σ 70
4.6 Geometría de la Separación Lineal de la Sección Normal 71
4.7 Separación Lineal 72
4.8 Separación Acimutal de la Sección Normal 74
vii

8. 4.9 El Arco Elíptico de una Sección Normal 76
4.10 El Elemento Diferencial en el Arco Elíptico 77
4.11 Efecto Acimutal para un Punto Elevado sobre el Elipsoide 78
4.12 Triángulo Pequeño para la Determinación del Efecto de Altura 79
4.13 El Ángulo de Declinación de la Cuerda 81
4.14 Sistemas de Coordenadas Local y Rectangular Espacial 84
4.15 El Sistema de Coordenadas Local 85
4.16 Traslado del Origen de los Ejes X, Y, Z al Punto A 86
4.17 Secciones Normales Entre Puntos Cercanos 89
4.17a La Geodésica entre Dos Secciones Normales 89
4.18 Una Geodésica y una Sección Normal en un Elipsoide Exageradamente
Achatado (f = 1/3) 90
4.19 Una Figura Diferencial en el Elipsoide 91
4.20 La Geodésica en una Forma Continua 95
4.21 Vista de una Geodésica Continua desde el Polo Norte Mostrando Cruces
Consecutivos en el Ecuador 96
4.22 La Superficie Elipsoidal Conteniendo un Elemento Diferencial de
Elipsoide 97
4.23 La Geodésica Localizada entre Dos Secciones Normales 101
4.24 Determinación de la Diferencial Acimutal entre una Sección Normal y una
Geodésica 102
4.25 Relación Diferencial entre Longitudes de Secciones Normales y
Geodésicas 104
4.26 La Curva de Alineación 106
5.1 Triángulos Esférico y Plano 109
5.2 Triángulos para el Método de Aditamento 116
6.1 El Triángulo Polar Elipsoidal 118
6.2 Aproximación de Puissant para Determinar la Latitud 127
6.3 Aproximación de Puissant para Determinar la Longitud 131
6.4 Triángulos Polares Resueltos Mediante las Fórmulas de la Latitud Media
de Gauss 135
6.5 Determinación Aproximada del Ángulo de Declinación 145
6.6 Sección de Meridiano Mostrando un Punto sobre el Elipsoide 149
6.7 Elipse Meridiana para la Derivación de Bowring 151
viii

9. 6.8 Geometría para la Determinación de h 153
7.1 Cantidades Astronómicas Medidas 159
7.2 La Esfera Celeste Mostrando Cantidades Astronómicas y Geodésicas 161
7.3 Determinación de las Distancias Cenitales 167
7.4 Ubicación del Geoide con Respecto al Elipsoide de Referencia de un
Datum Específico 170
7.5 Perfil Geoidal Astrogeodésico con Acimut α 171
7.6 Grilla Astrogeodésica 172
7.9 Reducción de la Línea Base (después de Heiskanen y Moritz, 1967) 175
7.10 Reducción de Distancias de Cuerda al Elipsoide 178
8.1 Efecto Diferencial de una Extensión Longitudinal 181
8.2 Efecto Diferencial de un Cambio de Acimut 183
8.3 Cambio del Retro-Acimut Debido a dα12 184
8.4 Detalle de los Efectos del Cambio de Retro-Acimut 185
9.1 Movimientos Diferenciales de los Puntos Extremos de la Línea 193
10.1 Tabla: Parámetros Elipsoidales 200
10.2 Sistema Satelital (S) y Datum (D) con Ejes Paralelos 201
10.2 Tabla: Parámetros de Transformación de Sistema Geodésico Local a
WGS84 203
ix

10. 1 INTRODUCCIÓN
La producción de mapas envuelve la determinación espacial de elementos sobre la superficie de
la Tierra y la transformación de sus posiciones en un plano. Las posiciones geográficas son
especificadas mediante coordenadas geodésicas. Para establecer un sistema de coordenadas
geodésico debemos primero conocer la forma y tamaño de la Tierra.
La Tierra es una figura geométrica muy suave. Para nosotros la Tierra parece muy accidentada,
pero aún los más altos montes y fosas oceánicas son casi imperceptibles en comparación con la
suave curvatura superficial. Para comprobarlo imaginemos la Tierra como una esfera de 1 m en
diámetro. El Monte Everest podría sobresalir como un abultamiento de 1,25 mm de altura y la
Fosa Mariana se vería como un rasguño de 1,73 mm de profundidad.
Desde el advenimiento de la era espacial, con el lanzamiento del primer satélite Sputnik, se ha
generado un incremento en la demanda del conocimiento preciso de los sistemas de referencia
geodésicos, como base para la determinación de coordenadas tanto en la superficie de la Tierra
como en el espacio. Del mismo modo, las agencias nacionales deben proveer las redes
geodésicas nacionales con la más alta precisión para cubrir las aplicaciones de posicionamiento,
navegación y proyectos de diferente orden que requieren de relaciones espaciales. Los
geodestas son los encargados de satisfacer estas necesidades, y para ello utilizan metodologías
rigurosas de medición y de análisis de resultados. En el presente texto se vierten las bases
teóricas del pilar fundamental de la geodesia, la geodesia geométrica.
1.1 Definiciones y Clasificación de la Geodesia
Siguiendo la definición clásica de Helmert (1887), “Geodesia es la ciencia que estudia el
tamaño, figura y campo gravitacional de la Tierra”
La palabra geodesia viene del griego, literalmente significa “dividir de la tierra”, y como primer
objetivo la práctica de la geodesia debería proveer un marco preciso para el control de las
mediciones topográficas nacionales. Por ello geodesia es la ciencia que determina el tamaño
y la forma de la Tierra y las relaciones de puntos seleccionados sobre la superficie de ella
mediante el uso de técnicas directas o indirectas. Estas características hacen de esta ciencia
una rama de las matemáticas aplicadas, la que debe incluir observaciones que puedan ser
usadas para determinar el tamaño y forma de la Tierra y la definición de sistemas de
coordenadas para posicionamiento en 3D; la variación de fenómenos cercanos a o sobre la
superficie, tales como gravedad, mareas, rotación de la Tierra, movimientos de la corteza y
deflexión de la línea de plomada; en conjunto con unidades de medida y métodos de
representación de la superficie de una Tierra curvada sobre una hoja de papel plano. (Smith,
1997)
Una definición mas contemporanea para geodesia es “Ciencia interdisciplinaria que utiliza
medios espaciales y medios aéreos remotamente censados, y mediciones basadas en la
1

11. Tierra para estudiar la forma y el tamaño de la Tierra, los planetas y sus satélites, y sus
cambios; para determinar en forma precisa posiciones y velocidades de puntos u objetos
que se encuentran en la superficie u orbitando el planeta, dentro de un sistema de
referencia terrestre definido, y para utilizar ese conocimiento a una variada gama de
aplicaciones científicas y de ingeniería, usando las ciencias matemática, física,
astronómica y computacional”1.
De lo anterior, podemos inferir que existen varias ramas en geodesia, entre ellas:
Geodesia Geométrica, Geodesia Física, Geodesia Astronómica, Geodesia Satelital, Geodesia
Planetaria y Geodesia Marina.
Geodesia puede ser dividida en tres áreas: Geodesia Global, Mediciones Geodésicas
Nacionales y Mediciones Planas. Geodesia global es responsable por la figura de la Tierra y el
campo de gravedad externo. Las mediciones geodésicas establecen los fundamentos para la
determinación de la superficie y el campo de gravedad externo de un país. Esto es
materializado mediante coordenadas y valores de gravedad en un número suficientemente
grande de puntos de control, arreglados en redes de control gravimétricas y geodésicas. En este
trabajo fundamental, deben ser consideradas la curvatura y el campo de gravedad de la Tierra.
En mediciones planas (mediciones topográficas, catastrales o ingenieriles), es obtenido el detalle
del terreno. En las mediciones geodésicas se utiliza un elipsoide de referencia para las
posiciones horizontales. En mediciones planas, generalmente es suficiente el plano horizontal.
(Torge, 1991)
1.2 Geodesia y Otras Disciplinas
Es tarea de la geodesia la definición de los sistemas de referencia y su materialización mediante
una red de puntos de control para el conocimiento de las relaciones espaciales que existen en la
Tierra. El uso primario de una red geodésica es georreferenciar la cartografía, la cual
representa, mediante el uso de una proyección cartográfica las relaciones espaciales del terreno
sobre una hoja de papel. Así podemos encontrar la geodesia relacionada con otras áreas de
estudio, como por ejemplo:
Ciencia espacial: esta requiere el conocimiento del campo de gravedad externo, de la superficie
de referencia terrestre, del sistema de referencia inercial o espacio fijo, y del sistema de
referencia geocéntrico o de tierra fija.
Astronomía: la geodesia determina el sistema de referencia casi inercial empleando técnicas de
radioastronomia; para ello, utilizando interferometría de base muy larga, desarrolla
observaciones de señales extragalácticas provenientes de quasares distantes entre 3 a 15
1
Ohio State University, Geodesy.
2

12. billones de años luz; el enlace al geocentro es efectuado utilizando mediciones de pulso láser
enviados a satélites.
Oceanografía: la reducción de observaciones satelitales al geoide es una actividad que se
desarrolla estableciendo una superficie equipotencial que basada en el nivel medio del mar
costero se proyecte mediante la nivelación y la gravedad hacia el interior de los continentes.
Ciencias Atmosféricas: la geodesia se encuentra experimentando la determinación del contenido
de agua en la atmósfera mediante el retraso de señales electromagnéticas desde o hacia satélites
en el espacio, ya sea por ocultamiento o por tomografía satelital.
Geología: la geodésia utiliza la gravedad para el establecimiento de superficies equipotenciales y
determinación de las alturas, estos datos también son válidos para inferir estructuras geológicas
subyacentes. Por su parte la geología utiliza las posiciones geodésicas para el control de
deformación de la corteza.
1.3 Bases Teóricas de la Geodesia
Matemáticas: este es el bloque de construcción más fuerte de la geodesia.
Estadística: la redundancia de datos en las observaciones geodésicas precisan utilizar modelos
estadísticos para análisis y determinación de parámetros geodésicos.
Computación: ésta es necesaria para el análisis y la automatización de los cálculos geodésicos.
Física: ésta entrega las bases teóricas para el estudio de las leyes de la gravitación, la
propagación de las ondas electromagnéticas y la mecánica del movimiento de los cuerpos, tanto
en el espacio como en la Tierra.
1.4 Historia de la Geodesia
La búsqueda del tamaño y forma de la Tierra tiene una larga e interesante historia. Aunque hoy
día no tenemos problemas en ver la Tierra como un cuerpo aproximadamente esférico, esta
situación no siempre existió.
Los registros de las primeras creencias indicaban que la Tierra era un disco plano que
soportaba un cielo hemisférico. Desde esa perspectiva debería existir solo un horizonte, con el
tiempo y la longitud del día independiente de la ubicación. (Homer siglo IX a.C.)
En el siglo VI a.C. Pitágoras enseñaba: los hombre deben vivir en un cuerpo de forma perfecta,
por ello la Tierra era esférica en forma. Esto sobre la base de que la esfera era considerada una
forma perfecta y no por deducción de observaciones.
3

13. Finalmente, en el siglo IV a.C. Aristóteles dio argumentos de porqué la Tierra debería tener
forma esférica. Algunas razones específicas que fueron mencionadas son:
- El cambio de horizonte cuando uno viaja en varias direcciones.
- La sombra redondeada de la Tierra sobre la Luna que fue observada en un eclipse lunar.
- Las observaciones de un barco en el mar donde el barco es visto más (o menos) según el
barco se aproxima (o se aleja).
Los sucesos siguientes ahora están relacionados con la determinación del tamaño de la tierra
esférica. Aunque otras determinaciones se hubieran hecho antes, el primer intento para lograr
una determinación precisa (en esa época), se le atribuye a Eratóstenes de Egipto. Los
acontecimientos en Egipto fueron una continuación natural a los adelantos hechos en
agrimensura con propósitos catastrales.
En el año 230 a.C., Eratóstenes, director de la gran biblioteca egipcia en Alejandría, realizó su
famoso experimento a fin de determinar el tamaño de la tierra esférica. Para ello efectuó
observaciones en dos ciudades egipcias, Alejandría y Siene (ahora Aswam), ubicadas ambas
casi en el mismo meridiano. En la ciudad más al sur, Siene, los rayos del sol iluminaban
directamente el fondo de un profundo pozo en el solsticio de verano, indicándo que el sol
estaba directamente arriba. Al año siguiente, en Alejandría se midió, al mediodía, la longitud de
una sombra proyectada por el gnomon de un reloj solar. Dicha longitud fue de 1/50 de 360°
(7°12’) y fue el ángulo subtendido en el centro de la tierra entre Siene y Alejandría, según se
muestra en la Figura 1.1.
θ
Rayos
Solares
ALEJANDRÍA
R s
SIENE
θ
Pozo
Figura 1.1 Geometría de la Medición de Eratóstenes
4

14. Si la distancia s, entre las dos ciudades pudiera deteminarse, y el ángulo θ, representara la
fracción de un círculo, la circunferencia de la Tierra sería s / θ. Alternadamente, el radio de la
tierra sería s / θ si θ estuviese ahora en radianes.
La determinación de la distancia entre ambas ciudades fue una materia dificil. La distancia
mayormente citada (la usada por Eratóstenes), es el valor redondeado de 5000 estadios. Esta
distancia fue probablemente determinada por contadores de pasos egipcios “quienes
determinaban distancias para los mapas egipcios”. Con este valor la circunferencia de la tierra
fue de 250.000 estadios. Otros cálculos indicaron que la circunferencia según la determinó
Eratóstenes era de 252.000 estadios, lo que quizás hubiera estado basado en una distancia más
específica.
La longitud de 1 estadio es, aproximadamente, 157,5 metros, lo que nos da un radio de 6.267
Krn, un 1,6 por ciento más pequeño que el actual radio medio.
El método usado por Eratóstenes estaba sujeto a una serie de errores. Por ejemplo, Alejandría
y Siene no están en el mismo meridiano, ni el Sol estaba directamente sobre el cenit al momento
de la medición. No obstante, el método funcionó bastante bien.
Esta experiencia fue repetida por Posidonio en el siglo primero A.C. En ese cálculo se midió un
arco a lo largo de un meridiano, desde Rodas hasta Alejandría. La separación angular se
determinó usando la estrella Canopus. Cuando ésta rasaba el horizonte en Rodas se hallaba en
un ángulo de 1/48 de un círculo completo en Alejandría. En consecuencia, la separación
angular entre las dos ciudades fue 7,5°. Por mediciones basadas en trayectos de buques de
vela se determinó que la distancia entre ambas poblaciones era de 5000 estadios. Esto significó
un radio inferior en 5,6 % de los cálculos presentes. Sucedió que la medición angular y de
distancia se mejoraron, aunque de una manera proporcional para que el resultado fuere
aproximadamente correcto. Por otro lado se rumorea que Posidonio no efectuó las mediciones
antes descritas, sino que más bien sólo discutió someramente el método.
En los siglos subsiguientes poco se hizo sobre estudios relacionados con la figura de la Tierra.
En el siglo IX, el califa Almamún mandó realizar nuevas mediciones cerca de Bagdad, Iraq, en
la planicie del río Eufrates. En esta aplicación se usaron varas de madera para medir la
extensión de un grado de latitud. Después de considerar el habitual problema de conversión de
unidades, las mediciones dieron un radio 10% más grande.
En el siglo XVII, Snellius llevó a cabo mediciones a lo largo de un meridiano en los Países
Bajos. Por primera vez usó un procedimiento de triangulación midiendo ángulos con un minuto
de precisión. Combinando esa medición con las latitudes astronómicas hechas en los puntos
finales del arco meridiano, Snellius determinó el tamaño de la Tierra esférica usando el método
básico de Eratóstenes. Una segunda determinación del radio (o realmente el cuadrante del
meridiano), dio un resultado de 3,4% más pequeño. Van Musschenbroek (sucesor de Snellius)
realizó trabajos adicionales obteniendo un radio terrestre mejorado.
Fue en esa época cuando comenzó la era de la geodesia esférica. En realidad se inició en 1666
cuando se estableció la Académe Royale des Sciencies con el fin de efectuar mediciones para
la preparación de un mapa preciso de Francia y la determinación del tamaño de la Tierra.
5

15. En 1670, Isaac Newton propuso que a consecuencia de su teoría de gravitación la Tierra
podría ser un poco abultada en el Ecuador debido a la mayor fuerza centrífuga generada por la
rotación terrestre. Este abultamiento podría producir un suave achatamiento en los polos de
aproximadamente 1/300 del radio ecuatorial.
En 1669, Picard nició la medición de un arco meridiano cerca de París. Entre 1683-1716, el
arco se extendió hacia el sur, a Collioure, y a Dunquerque hacia el norte, por un grupo dirigido
por Lahire y los Cassini, Dominique y Jacque. Los cálculos hechos sobre esas mediciones
indicaron que la extensión del arco meridiano era más pequeña hacia los polos. Esta conclusión
tentativa estaba en conflicto con la idea de que la Tierra tenía una forma esférica. De hecho,
denotaba que la Tierra estaba apuntando hacia los polos, según se muestra en la Figura 1.2:
Figura 1.2 La Forma de la Tierra según las Antiguas Mediciones Francesas
Estas mediciones también eran conflictivas con las teorías propuestas por Isaac Newton que
sugerían que la Tierra debería estar achatada en los polos. Esto implicaría que al viajar hacia
el Ecuador nos alejaríamos más del centro de la Tierra. El efecto de esto fue observado por
Richter (en 1672) en los relojes de péndulo que aunque mantenían la hora debida en París,
perdían 2½minutos por día al llevarlos a Cayena, Guyana Francesa, cerca del Ecuador en
Sudamérica. Esa pérdida de tiempo era consecuente con la teoría de Newton por la
disminución de la gravedad al ir de París a Cayena.
Para resolver esta situación, la Real Academia de Ciencias preparó dos misiones de
levantamientos geodésicos. Una expedición (1734-1741) se mandó al Perú (hoy Ecuador) en
una latitud de –1,5’ bajo la dirección de Godin, La Condamine y Bouguer. La segunda
expedición (1736-1737) se envió a Laponia (latitud de unos 66.3°) bajo la dirección de
Maupertuis y Clairaut. Los resultados de dichas mensuras indicaron que la extensión de un
6

16. meridiano de 1° era superior en las regiones polares que en las ecuatoriales. Este resultado
concordó con las teorías de Newton e implicó que la figura de la Tierra podría representarse
por un elipsoide ligeramente achatado en los polos, según se observa en la Figura 1.3:
b
a
Figura 1.3 Elipse Achatada en los Polos
Un cálculo actual del radio ecuatorial (a) de la Tierra es de 6378137 metros. El achatamiento
a−b
(f = ) es aproximadamente 1/298.257, lo que significa una diferencia de 21.7 km. entre
a
el radio ecuatorial y el radio polar.
Se efectuaron otras mediciones -Svanberg (1805) en Suecia, Lacaille (1751) en Sudáfrica,
Gauss (1821-23), Bessel (1831-38)- para verificar y perfeccionar el conocimiento del tamaño
y forma de la Tierra. Hoy día continúan estudios para refinar tales conocimientos. Al disponer
de mejoradas técnicas de medición se hizo evidente el definir más exactamente lo que llamamos
la figura de la Tierra.
Para hacerlo, consideremos la superficie topográfico real de la Tierra, y una superficie
estrechamente asociada con la superficie del océano. Reconocemos que los océanos
comprenden aproximadamente el 70% de la superficie terrestre. Por tanto es correcto visualizar
la figura del Tierra como aquella de la superficie oceánica. En l872-73, Listing introdujo el
concepto del geoide como la superficie del mar imperturbable y su continuación en los
continentes. El elipsoide de los estudios previos ahora se convirtió en una aproximación al
geoide.
En 1884, Helmert definió con mayor precisión el geoide identificándolo como un océano sin
peregrinaciones tales como las causadas por mareas, vientos, olas, temperaturas, presión
diferencias en salinidad, etc. Este geoide se consideró como una superficie equipotencial del
7

17. campo de gravedad de la Tierra. El geoide en áreas continentales se visualizaría por el nivel del
agua en infinitamente pequeños canales “secos” en tierra.
Por desgracia, la definición del geoide antes mencionada no es totalmente realizable. Esto es así
porque la superficie del océano es una superficie dinámica, en constante cambio debido a tantas
corrientes, etc. Sin embargo, estos efectos generalmente ocurren a un metro de nivel por lo que
para muchos propósitos podemos identificar el nivel medio del mar como el geoide.
De nuevo indicamos que ahora se usa el elipsoide para aproximarnos al geoide. Aunque hay
varios tipos de elipsoide, el usado mayormente en geodesia es un elipsoide de revolución
(alrededor del eje menor) que es simétrico con respecto al Ecuador. Otro es el elipsoide
triaxial, en el cual el Ecuador es una elipsoide. No obstante, los cálculos en un elipsoide triaxial
son bastantes complicados con respecto a los del elipsoide biaxial rotacional simétrico.
Consecuentemente, en este tema de geodesia geométrica nos concentraremos en la geometría e
importancia geodésica del elipsoide.
Usando una sección meridiana de la Tierra, en la Figura 1.4, se representan las distintas
superficies que hemos estado revisando.
Superficie
Topográfica
H
h
b
N
Geoide
a
Elipsoide
Figura 1.4 Relación entre Elipsoide, Terreno y Geoide
Podríamos poner en perspectiva las magnitudes de varias cantidades de interés. Recuérdese
que el radio ecuatorial de la Tierra es aproximadamente 6378137 metros. Con respecto a un
elipsoide cuyo centro está en el centro de la tierra, la desviación estandar de la ondulación del
geoide (N) es 30.56 m con valores extremos aproximados de –107 m y 85 m. Finalmente, el
terreno tiene una elevación máxima con respecto al nivel medio del mar de unos 9 km.
La información histórica descrita aquí ha sido basada en dos documentos de Irene Fisher
(1975a, 1975b).
8

18. 2 PROCEDIMIENTOS MATEMÁTICOS ÚTILES
En el desarrollo de algunas ecuaciones que siguen en los apuntes será de utilidad emplear
ciertos procedimientos matemáticos estándares que envuelven expansiones en series e
identidades trigonométricas. Las usadas más ampliamente serán tratadas a continuación.
2.1 Series de Taylor y Maclaurin
Una función f(x) puede ser expandida sobre un punto x 0 usando una serie de Taylor:
( x − x0 ) 2 ( x − x0 ) 3
f ( x ) = f ( x0 ) + ( x − x0 ) f ' ( x0 ) + f ' ' ( x0 ) + f ' ' ' ( x0 ) + ... (2.1)
2! 3!
Donde f’(x 0) es la 1a derivada de f(x) evaluada en x 0 y sucesivamente para los otros términos
primos. En principio uno debe controlar la convergencia de esta serie, pero para la mayor
cantidad de las aplicaciones de la geodesia geométrica, esta será rápida.
En algunos casos es conveniente utilizar x-x 0 = h y x = x 0, así, (2.1) queda;
f ( x + h) = f ( x) + hf ' ( x) + h2
2!
f ' ' (x ) + h3
3!
f ' ' ' ( x ) + ... (2.2)
Como un ejemplo considere f(x) = sen(x). Aplicando (2.2), tenemos:
sin( x + h) = sin x + h cos x − h2 sin x − cos x + sin x + − − −
2
h3 h4
6 24 (2.3)
Un caso especial de las series de Taylor es la de Maclaurin, la cual se encuentra usando (2.1)
haciendo x 0 = 0, de ese modo queda:
f ( x ) = f (0) + xf ' (0) + x2
2!
f ' ' ( 0) + x3
3!
f ' ' ' ( 0) + − − − (2.4)
Un nuevo ejemplo, tomemos f(x) = sin(x). Entonces (2.4) se transforma en:
9

19. x3 x5 x 7
sin x = x − + − +−−− (2.5)
3! 5! 7!
2.2 Las Series Binomiales
Otra serie útil es la serie binomial, la cual puede ser escrita como:
n ( n −1 ) n ( n −1)( n − 2 )
(1 ± x) n = 1 ± nx + 2!
x2 ± 3!
x3 + − − − (2.6)
Los coeficientes de x, x 2, x 3, etc. son llamados coeficientes binomiales.
Las series binomiales existen por integración o exponentes fraccionales positivos o negativos y
siempre convergen si x < 1. Las expresiones siguientes son series binomiales útiles:
1
1− x
= 1 + x + x 2 + x 3 + x 4 + ...
1
1+ x
= 1 − x + x 2 − x 3 + x 4 − ...
1
(1+ x ) 2
= 1 − 2 x + 3x 2 − 4 x3 + 5 x 4 − ...
1
(1− x ) 2
= 1 + 2 x + 3x 2 + 4 x 3 + 5 x 4 + ...
(2.7)
1 + x = 1 + 1 x − 1 x 2 + 16 x 3 − 128 x 4 +
2 8
1 5 7
256
x 5 − 1024 x 6 +
21 33
2048
x7 − ...
1 − x = 1 − 1 x − 1 x 2 − 16 x 3 − 128 x 4 − ...
2 8
1 5
1
1+ x
= 1 − 1 x + 3 x 2 − 16 x 3 + 128 x 4 − 256 x 5 + 1024 x6 − 2048 x7 + ...
2 8
5 35 63 231 429
1
1− x
= 1 + 1 x + 3 x 2 + 16 x 3 + 128 x 4 + ...
2 8
5 35
10

20. 1 − x 2 = 1 − 1 x 2 − 1 x 4 − 16 x 6 − 128 x8 −
2 8
1 5 7
256
x10 − ...
1
= 1 + 1 x 2 + 3 x 4 + 16 x 6 + 128 x8 +
2 8
5 35 63
256 x10 + ...
1− x 2
2.3 Inversión de Series
Otras importantes series relacionadas son las series de inversión. Un tipo relaciona la inversión
de series de convergencia algebraica, mientras que otro relaciona la inversión de series
trigonométricas. Considere primero las siguientes series de potencias:
y = a1 x + a2 x 2 + a3 x 3 + a4 x 4 + ... (2.8)
La inversión de (2.8) se transforma en la forma general:
x = A1 y + A2 y 2 + A3 y 3 + A4 y 4 + ... (2.9)
donde:
1
A1 =
a1
a2
A2 = −
(a1 )3
( 2(a2 ) − a1 a3 );
1
A3 =
2
(2.10)
(a1 )5
(5a1 a2 a3 − (a1 ) a4 − 5(a2 ) );
1
A4 =
2 3
(a1 ) 7
11

21. ( 6(a1 )2 a2 a4 + 3(a1 a3 )2 + 14(a2 )4 − (a1 )3 a5 − 21a1 (a2 )2 a3 ).
1
A5 =
(a1 )9
Considere ahora una expansión escrita en la siguiente forma (Ganshin, 1967, pág.9)
tan y = p tan x (2.11)
Entonces:
y − x = q sin 2 x + 1 q 2 sin 4 x + 1 q 3 sin 6 x + ...
2 3 (2.12)
donde:
q= p −1
p +1
Otra fórmula importante es la siguiente:
y = x + P2 sin 2 x + P4 sin 4 x + P6 sin 6 x + − −
La inversión de esta ecuación es:
x = y + P2 sin 2 y + P4 sin 4 y + P6 sin 6 y + − −
donde (Ganshin, 1967, pág.32):
P2 = − P2 − P2 P4 + 1 P23 − P6 P4 + P2 P42 − 1 P22 P6 + 1 P23 P4 − 12 P25 ± − − −
2 2 3
1
P4 = − P4 + P22 − 2 P2 P6 + 4 P22 P4 − 4 P24 ± − − −
3
12

22. P6 = −P6 + 3P2 P4 − 3 P23 − 3 P2 P8 + 9 P2 P42 + 9 P22 P6 −
2 2
27
2
P23 P4 + 27 P25 ± − − −
8
P8 = − P8 + 2 P42 ± 4 P2 P6 − 8P22 P4 + 8 P24 ± − − −
3
P = − P10 + 5 P4 P6 + 5P2 P − 25 P22 P6 − 25 P2 P42 + 125 P22 P4 − 125 P25 ± − − −
10 8 2 2 6 4
2.4 Resumen de Expansiones Trigonométricas
Usando la serie de Maclaurin revisada previamente las siguientes expansiones pueden ser
derivadas donde x es un ángulo en radianes:
sin x = x − x3
3! + x5
5! − x7
7! ± −−− (2.13)
cos x = 1 − x2
2!
+ x4
4!
− x6
6!
+−−− (2.14)
tanx = x + x3
+ 215 + 17 x + − − −
5 7
x
3 315
(2.15)
y3 3 y5 7
x = sin −1 y = y + 6 + 40 + 5y + − − −
112 (2.16)
y3 y5 y7
x = tan −1 y = y − 3
+ 5
− 7
+ −−− (2.17)
2.5 Fórmulas de Ángulo Múltiple
Para cierto número de aplicaciones es conveniente tener fórmulas relativas a potencias de sin(x)
o cos(x) para fórmulas de ángulos múltiple. Tales como:
sin 2 x = 1 − 1 cos 2 x
2 2
13

23. sin 3 x = 3 sin x − 1 sin 3x
4 4
sin 4 x = 3 − 1 cos 2 x + 1 cos 4 x
8 2 8
sin 5 x = 5 sin x − 16 sin 3 x + 16 sin 5 x
8
5 1
sin 6 x = 16 − 15 cos 2 x + 16 cos 4 x −
5
32
3 1
32 cos 6 x
sin 7 x = 35
64 sin x − 21
64 sin 3 x + 7
64 sin 5 x − 64 sin 7 x
1
(2.18)
sin 8 x = 35
128 − 16 cos 2 x +
7 7
32 cos 4 x − 16 cos 6 x + 128 cos 8 x
1 1
sin 9 x = 128 snx − 21 sin 3x + 64 sin 5x − 256 sin 7 x +
63
64
9 9 1
256 sin 9 x
sin 10 x = 63
256 − 105 cos 2 x +
256
15
64 cos 4 x − 512 cos 6 x + 256 cos 8x − 512 cos 10 x
45 5 1
cos 2 x = 1 + 1 cos 2 x
2 2
cos 3 x = 3 cos x + 1 cos 3 x
4 4
cos 4 x = 3 + 1 cos 2 x + 1 cos 4 x
8 2 8
cos 5 x = 5 cos x + 16 cos 3 x + 16 cos 5 x
8
5 1
cos 6 x = 16 + 15 cos 2 x + 16 cos 4 x +
5
32
3 1
32
cos 6 x (2.19)
cos 4
x = 3
8
+ 1
2
cos 2 x + 1
8
cos 4 x
14

24. cos 8 x = 128 + 16 cos 2 x + 32 cos 4 x + 16 cos 6 x + 128 cos 8 x
35 7 7 1 1
cos 9 x = 128 cos x +
63 21
64
cos 3x + 64 cos 5 x +
9 9
256
cos 7 x + 256 cos 9 x
1
cos10 x = 63
256
+ 105
256
cos 2 x + 15 cos 4 x + 512 cos 6 x +
64
45 5
256
cos 8x + 512 cos 10 x
1
sin 2 x = 2 sin x cos x
sin 3x = 3 sin x cos 2 x − sin 3 x
sin 4 x = 4 sin x cos 3 x − 4 sin 3 x cos x
sin 5 x = 5 sin x cos 4 x − 10 sin 3 x cos 2 x + sin 5 x (2.20)
sin 6 x = 6 sin x cos 5 x − 20 sin 3 x cos 3 x + 6 sin 5 x cos x
sin 7 x = 7 sin x cos 6 x − 35 sin 3 x cos 4 x + 21 sin 5 x cos 2 x − sin 7 x
sin 8x = 8 sin x cos 7 x − 56 sin 3 x cos 5 x + 56 sin 5 x cos 3 x − 8 sin 7 x cos x
sin 9 x = 9 sin x cos 8 x − 84 sin 3 x cos 6 x + 126 sin 5 x cos 4 x − 36 sin 7 x cos 2 x + sin 9 x
sin 10 x = 10 sin x cos 9 x − 120 sin 3 x cos 7 x + 252 sin 5 x cos 5 x − 120 sin 7 x cos 3 x + 10 sin 9 x cos x
cos 2 x = cos 2 x − sin 2 x
cos 3 x = cos 3 x − 3 cos x sin 2 x
cos 4 x = cos 4 x − 6 cos 2 x sin 2 x + sin 4 x
15

25. cos 5 x = cos 5 x − 10 cos 8 x sin 2 x + 5 cos x sin 4 x
cos 6 x = cos 6 x − 15 cos 4 x sin 2 x + 15 cos 2 x sin 4 x − sin 6 x (2.21)
cos 7 x = cos 7 x − 21 cos 5 x sin 2 x + 35 cos 3 x sin 4 x − 7 cos 6 x sin 6 x
cos 8 x = cos 8 x − 28 cos 6 x sin 2 x + 70 cos 4 x sin 4 x − 28 cos 2 x sin 6 x + sin 8 x
cos 9 x = cos 9 x − 36 cos 7 x sin 2 x + 126 cos 5 x sin 4 x − 84 cos 3 x sin 6 x + 9 cos x sin 8 x
cos 10 x = cos 10 x − 45 cos 8 x sin 2 x + 210 cos 6 x sin 4 x − 210 cos 4 x sin 6 x + 45 cos 2 x sin 8 x − sin 10 x
Otras identidades útiles para dos ángulos X e Y son las siguientes:
sin nX − sin nY = 2 cos n ( X + Y ) sin n ( X − Y )
2 2 (2.22)
cos nX − cos nY = 2 sin n ( X + Y ) sin n ( X − Y )
2 2 (2.23)
16

26. 3 PROPIEDADES DEL ELIPSOIDE
3.1 Introducción
Según se trató en la Sección 1, en geodesia geométrica, para muchos cálculos se debe
lidiar con la geometría de un elipsoide de revolución. Este elipsoide es formado mediante
la rotación de su semieje menor.
Consideremos el elipsoide que se muestra en la Figura 3.1.
z
P1
P
b
A a B
O x
F2 F1
P2
Figura 3.1 La Elipse Básica
En la figura tenemos:
F1 , F2 , focos de la elipse AP 2 BP1 .
O, centro de la elipse.
OA = OB = a = semieje mayor de la elipse.
OP1 = OP2 = b = semieje menor de la elipse.
P1 P2 , es el eje menor de la elipse, mientras que P es un punto arbitrario en la elipse.
17

27. De la definición de una elipse, el movimiento de P sobre la elipse produce una suma
constante de las distancias tomadas desde dos puntos fijos, denominados focos.
F1 P + F2 P = constante (3.1)
Si dejamos mover a P en dirección hacia B, y luego en dirección hacia A, encontramos
que:
F1 P + F2 P = 2a (3.2)
Si ahora dejamos P ir hacia P1 , se verifica que F1 P = F2 P, de la ecuación (3.2) se tiene que
F1 P = F2 P = a, el semieje mayor. Esta información es mostrada en la figura siguiente:
z
P1
α
b a
(a 2 -b 2 )1/2 x
F2 O F1
P2
Figura 3.2 Notación para la Elipse
Ahora estamos en posición de definir algunos parámetros fundamentales de la elipse.
Tenemos lo siguiente:
a−b
1) El achatamiento polar, f: f = (3.3)
a
OF1 a2 − b2 2 a2 − b2
2) La primera excentricidad, e: e ≡ = ;e = (3.4)
a a a2
18

28. OF1 a2 − b2 2 a2 − b2
3) La segunda excentricidad, e': e' ≡ = ;e ' = (3.5)
b b b2
4) Excentricidad angular, α (ver figura 3.2); α es el ángulo en P1 entre el semieje menor y
la línea dibujada desde P hasta ya sea F1 o F2 . Tenemos:
b
cosα = =1− f (3.6)
a
OF1
sin α = =e (3.7)
a
OF1
tan α = = e' (3.8)
b
5) Excentricidad lineal, E: E = ae (3.9)
Otras dos cantidades usadas a menudo, son:
a2 − b2
m= (3.10)
a2 + b2
a−b
n= (3.11)
a+b
en algunos libros la cantidad m es designada como e’’2
Los parámetros básicos a, b, f, e, e’, α, m, n, son interrelacionados a través de ecuaciones
que pueden ser fácilmente derivadas. Por ejemplo, considere las relaciones entre f y e’.
Desde (3.4) tenemos:
b
e2 =1− (3.12)
a2
de (3.3):
b
=1− f (3.13)
a
la cual es sustituida dentro de (3.12) para encontrar:
19

29. e2 = 2 f − f 2 (3.14)
Otras relaciones de interés son como sigue: (Gan’shin, 1967):
e '2 4n 2m
e = 2 = 2 =
2
(3.15)
1 + e' (1 + n ) 1 + m
e2
e' =
2
(3.16)
1− e2
(1 − e )(1 + e' ) = 1
2 2
(3.17)
1−n 1− m
= (1 − f ) = 1 − e 2 = =
b e 1
= = (3.18)
a e' 1 + e' 2 1+ n 1+ m
f 1 − 1 − e2
n= = (3.19)
2 − f 1 + 1 − e2
2f − f 2 2n
m= = (3.20)
1 + (1 − f ) 1 + n2
2
Adicionalmente, en ocasiones es conveniente tener algunas expresiones en serie
relacionando ciertas cantidades. Por ejemplo, tenemos las siguientes (Gan’shin, 1967):
n = (1 / 2) f + (1 / 4) f 2 + (1 / 8) f 3 + (1 / 16) f 4 + (1 / 32) f 5 +
n = (1 / 4)e 2 + (1 / 8)e 4 + ( 5 / 64)e 6 + ( 7 / 128)e 8 + (21 / 512) e10 +
n = (1 / 2)m + (1 / 8) m 3 + (1 / 16)m 5 +
m = f + (1 / 2) f 2 − (1 / 4) f 4 − (1 / 4) f 5 +
20

30. m = (1 / 2) e 2 + (1 / 4) e 4 + (1 / 8)e 6 + (1 / 16)e 8 + (1 / 32)e 10 +
m = 2n − 2n 3 + 2n 5 +
e' 2 = 2 f + 3 f 2 + 4 f 3 + 5 f 4 + 6 f 5 +
e' 2 = 4n + 8n 2 + 12n 3 + 16 n 4 + 20n 5 +
e' 2 = 2m + 2 m 2 + 2m 3 + 2m 4 + 2m 5 +
Los valores numéricos de estas cantidades dependen de la definición fundamental de
parámetros tales como: tamaño (a) y forma (usualmente f). Muchos elipsoides diferentes
han sido usados en el pasado. Actualmente el sistema de constantes recomendado por la
Asociación Internacional de Geodesia (IAG) es el Sistema de Referencia Geodésico de
1980 (Moritz, 1980). Para este sistema, las cantidades de interés geométrico son las
siguientes:
a = 6378137 m (exacta)
b = 6356752.3141 m
E = 521854.0097 m
c = 6399593.6259 m
e2 = 0.00669438002290
e’2 = 0.00673949677548
f = 0.00335281068118
f – 1 = 298.257222101
n = 0.001679220395
m = 0.003358431319
Q = 10001965.7293 m
R1 = 6371008.7714 m
R2 = 6371007.1810 m
R3 = 6371000.7900 m
21

31. En las constantes de arriba Q es la longitud de un cuadrante de meridiano, R1 es el radio
medio (2a + b) / 3, R2 es el radio de una esfera que tiene igual superficie que el área del
elipsoide, y R3 es el radio de una esfera que tiene igual volumen que el elipsoide. La
derivación de las ecuaciones para estas cantidades será tratada en secciones posteriores.
3.2 Coordenadas Geodésicas
Consideramos primero un elipsoide de revolución cuyo centro está en O. Definimos el eje
OZ como el eje de rotación del elipsoide. El eje OX se subtiende en el plano ecuatorial e
intercepta el meridiano PEP1 , el cual es tomado como el primer meridiano o meridiano
inicial desde donde las longitudes serán medidas. El eje OY está en el plano ecuatorial,
perpendicular al eje OX tal que OX, OY, OZ forman un sistema coordenado de mano
derecha como se muestra en la Figura 3.3.
Z
P Q’
λ
Q
ϕ
O Y
λ
E
X
P1
Figura 3.3 Sistema de Coordenadas para el Elipsoide
Un punto arbitrario Q o Q’ (dentro o fuera de la superficie del elipsoide) puede ser
definido entonces por sus coordenadas X, Y, Z.
Deberíamos observar que sobre un meridiano cualquiera, tal como PQP1 o PEP 1 , la
longitud es una constante para cualquier punto localizado en este plano meridiano. La
longitud geodésica λ de un punto es definida como el ángulo diedro entre los planos del
primer meridiano (PEP1 ) y un meridiano (ejemplo PQP1 ) que está pasando a través del
punto dado. Las longitudes, en este apunte y para muchos casos son medidas positivas
22

32. hacia el Este, aunque hay casos (ejemplo EE.UU. y Chile) donde algunas referencias
consideran que las longitudes medidas hacia el Oeste de Greenwich también son
positivas.
La latitud geodésica ϕ de un punto ubicado sobre la superficie del elipsoide, es definida
como el ángulo entre la normal al elipsoide en el punto y el plano ecuatorial. Para un
punto ubicado sobre la superficie del elipsoide hay varias definiciones posibles. La más
simple es que éste es el ángulo entre la normal al elipsoide, que está pasando a través de
este punto, y el plano ecuatorial. Este sistema de coordenadas (por ejemplo ϕ, λ) es
llamado coordenadas geodésicas (en algunos libros podrían ser encontradas algunas
referencias a coordenadas geográficas, las cuales son idénticas a las coordenadas
geodésicas). ϕ y λ forman un juego de coordenadas curvilíneas sobre la superficie del
elipsoide. Ellas permiten la descripción de muchas propiedades involucradas con la
superficie y curvas sobre la superficie.
3.3 La Elipse Meridiana
La elipse meridiana que pasa a través del punto Q es mostrada en la Figura 3.4 con los
ejes coordenados z y x.
z
Q
ϕ 90°+ ϕ
x
Figura 3.4 Elipse Meridiana
Además de la latitud geodésica podemos definir la latitud reducida β y la latitud
geocéntrica ψ. La latitud reducida (algunas veces llamada latitud paramétrica) es el
ángulo cuyo vértice se ubica en el centro de una esfera que es tangente al elipsoide a lo
largo del Ecuador, entre el plano ecuatorial y el radio del punto P originado en la esfera
1
por una línea recta perpendicular al plano del Ecuador, que pasa a través del punto P
23

33. sobre el elipsoide, para el cual la latitud reducida está siendo definida. La latitud reducida
es mostrada en la Figura 3.5.
z
P1
P
a
z
β
x
O x P2
Figura 3.5 Latitud Reducida
La latitud geocéntrica es el ángulo en el centro de la elipse entre el plano del Ecuador y
una línea hacia el punto cuya latitud geocéntrica está siendo definida. Observe que esta
definición permite un significado simple para definir esta latitud aunque el punto podría
no estar localizado sobre la superficie del elipsoide. La latitud geocéntrica es mostrada en
la Figura 3.6.
z
P
r
z
ψ
x
O x P2
Figura 3.6 Latitud Geocéntrica
24

34. Las coordenadas z y x pueden ser calculadas conociendo ya sea ϕ, β, o ψ más los
parámetros del elipsoide. Estas relaciones son útiles en la derivación de expresiones que
relacionan las latitudes.
Consideramos primero la determinación de x y z usando la latitud reducida β. Desde la
Figura 3.5 tenemos:
(OP2 ) 2 + ( P2 P1 ) 2 = a 2 (3.22)
La ecuación de esta elipse puede ser escrita:
x2 z 2
+ =1 (3.23)
a2 b2
o con x = OP 2 y con z = P2 P, tenemos:
(OP2 )2 + (P2 P) 2 =1 (3.24)
a2 b2
Combinando (3.22) y (3.24), queda:
a2
(OP2 ) + ( P2 P ) 2 = a 2 = (OP2 ) 2 + ( P2 P1 ) 2
2 2
(3.25)
b
Resolviendo para P2 P, encontramos:
b
P2 P = P2 P1 (3.26)
a
De la Figura 3.5 tenemos que:
P2 P1 = a sin β (3.27)
25

35. luego las coordenadas x y z son:
x = OP2 = a cos β (3.28)
z = P2 P = b sin β (3.29)
Para determinar x y z usando la latitud geodésica observamos, considerando la Figura 3.4,
que la pendiente de la línea tangente es la tangente del ángulo con los ejes positivos.
dz − cos ϕ
= tan( 90 + ϕ) = − cot ϕ = (3.30)
dx sin ϕ
dz
donde es la inclinación de la línea tangente. Para determinar la derivada reescribimos
dx
la ecuación (3.23) como sigue:
b 2 x 2 + a 2 z 2 = a 2b 2 (3.31)
y diferenciamos para conseguir,
b 2 xdx + a 2 zdz = 0 (3.32)
o arreglando:
dz − b 2 x − cos ϕ
= 2 = (3.33)
dx a z sin ϕ
Usando la ecuación (3.26) y (3.33) queda:
b 2 x sin ϕ = a 2 z cos ϕ (3.34)
Elevando al cuadrado ambos lados queda:
26

36. b 4 x 2 sin 2 ϕ − a 4 z 2 cos 2 ϕ = 0 (3.35)
Entonces multiplicando la ecuación (3.31) por –b2 sin2 ϕ, agregando el resultado a la
ecuación (3.35) y multiplicando por –1, y entonces resolviendo para z encontramos:
b 2 sin ϕ
z= (3.36)
a 2 cos 2 ϕ + b 2 sin 2 ϕ
Utilizando un procedimiento similar, encontramos para x:
a 2 cos ϕ
x= (3.37)
a 2 cos 2 ϕ + b 2 sin 2 ϕ
Usando e2 de la ecuación (3.4) los denominadores de la ecuación (3.36) y (3.37) se
convierten en (1-e2 sin2 ϕ)½ de modo que x y z pueden expresarse como:
a cos ϕ
x= (3.38)
1 − e 2 sin 2 ϕ
z=
( )
a 1 − e 2 sin ϕ
(3.39)
1 − e 2 sin 2 ϕ
En este punto es conveniente introducir y definir cuatro nuevas cantidades:
W 2 ≡ 1 − e 2 sin 2 ϕ
V 2 ≡ 1 + e' 2 cos 2 ϕ
(3.40)
w ≡ 1 − e cos β
2 2 2
v 2 ≡ 1 − e '2 sin 2 β
27

37. Comenzando desde estas designaciones, varias otras relaciones pueden ser derivadas.
1
W2 =
1 + e' sin 2 β
2
(3.41)
1
V2 =
1 − e cos 2 β
2
Usando W y V en las ecuaciones (3.38) y (3.39) podemos escribir:
a cos ϕ
x= (3.42)
W
a(1 − e ) sin ϕ
z= (3.43)
W
c
x= cos ϕ (3.44)
V
c sin ϕ
z= (3.45)
V (1 + e' 2 )
a2
donde c = . Una interpretación geométrica para c será entregada posteriormente.
b
Puede agregarse un significado geométrico a W y V considerando los elementos de la
Figura 3.7.
28

38. Z
P
q
z
ϕ
ϕ
X
x
Figura 3.7 Interpretación Geométrica de W y V
q es una distancia medida desde el origen hasta el plano tangente que pasa por P (cuya
latitud geodésica es ϕ ) de tal forma que la línea trazada desde el origen es perpendicular
al plano tangente. Tenemos:
q = x cos ϕ + z sin ϕ (3.46)
Sustituyendo x y z de las ecuaciones (3.42) y (3.43) queda:
q = aW (3.47)
De (3.44) y (3.45) tenemos:
q = bV (3.48)
29

39. Podemos igualar (3.47) y (3.48) para finalmente escribir:
b
W = V (3.49)
a
A continuación pasamos a la determinación de x y z usando la latitud geocéntrica. De la
Figura 3.6 escribimos:
x = r cos ψ (3.50)
z = r sin ψ (3.51)
donde r es el radio geocéntrico.
Claramente tenemos:
r = x2 + z2 (3.52)
Substituyendo (3.50) y (3.51) en la ecuación (3.23), y resolviendo para r queda:
a 1−e2 b
r= = (3.53)
1 − e cos ψ
2 2
1 − e cos 2 ψ
2
Substituyendo este valor de r de regreso dentro de (3.50) y (3.51), obtenemos:
a 1 − e 2 cosψ
x= (3.54)
1 − e 2 cos 2 ψ
a 1 − e 2 sin ψ
z= (3.55)
1 − e 2 cos 2 ψ
30

40. También podríamos obtener una expresión para el vector del radio en términos de la
latitud geodésica si sustituimos las ecuaciones (3.38) y (3.39) en (3.52):
r=
a
W
( )
1 + e 2 e 2 − 2 sin 2 ϕ (3.56)
Puesto que el segundo término a la derecha de (3.56) está en el orden de e2 , es
conveniente obtener una expresión en serie para el vector del radio. Primero
desarrollamos el término de raíz cuadrada usando la serie binomial (ecuación 2.7) para
que:
r=
a  1 2 2
( 1 4
) 
1 + e e − 2 sin ϕ − e sin ϕ + ...
2 4
(3.57)
W 2 2 
1
Ahora calculamos usando un desarrollo en serie de McLaurin (ecuación 2.4):
W
1 e2 3
= 1 + sin 2 ϕ + e 4 sin 4 ϕ + ... (3.58)
W 2 8
Multiplicando (3.57) y (3.58) hallamos una expresión en serie para r en términos de la
latitud geodésica:
 e2 e4 5 3 13 
r = a1 − sin ϕ + sin 2 ϕ − e 4 sin 4 ϕ + e 6 sin 4 ϕ − e 6 sin 6 ϕ + ...
2
(3.59)
 2 2 8 4 16 
El número de términos a retenerse en tal expresión depende de la exactitud deseada.
Recordemos que para el Sistema de Referencia Geodésico 1980, a = 6378137 m, e2 =
0,00669..., los últimos dos términos en la ecuación (3.59) tienen un valor máximo de
0,0008 metros.
31

41. 3.4 Relaciones entre las Diferentes Latitudes
Podemos usar algunas de las ecuaciones previamente deducidas para obtener relaciones
entre las latitudes descritas. De la Figura 3.6 escribimos:
z
tan ψ = (3.60)
x
Sustituyendo z y x de las ecuaciones (3.28), (3.29) y (3.38), (3.39) tenemos:
tan β = (1 − e 2 ) tan ϕ
b
tan ψ = (3.61)
a
Entonces:
( )
tan ψ = 1 − e 2 tan β = 1 − e 2 tan ϕ (3.62)
tan β = 1 − e 2 tan ϕ (3.63)
tan ϕ = 1 − e'2 tan β (3.64)
Aunque estas relaciones son suficientes para determinar un tipo de latitudes desde
cualquier otro, algunos procedimientos se simplifican si también se encuentran otras
relaciones. Por ejemplo, igualamos la coordenada z en (3.29) y (3.43) para obtener:
1 − e 2 sin ϕ sin ϕ
sin β = = (3.65)
W V
Igualando las ecuaciones (3.28) y (3.42) que tratan con la coordenada x, tenemos:
cos ϕ
cos β = (3.66)
W
32

42. Otras relaciones de interés incluyen:
cos β 2 cos β
cos ϕ = v = 1− e w (3.67)
sin β 2 sin β
sin ϕ = w = 1+ e' v (3.68)
Seguidamente pasamos a la determinación de expresiones para establecer la diferencia
entre dos tipos de latitudes. Primero consideramos las expresiones cerradas y luego las
expresiones en serie. Ahora consideraremos la diferencia entre la latitud geodésica y la
reducida, escribiendo:
sin (ϕ − β) = sin ϕ cos β − cos ϕ sin β (3.69)
Luego sustituimos los valores de sin β y cos β de (3.65) y (3.66) para obtener después
de algunas reducciones:
f sin 2ϕ
sin (ϕ − β) = (3.71)
2W
Otra expresión cerrada puede escribirse comenzando de la siguiente identidad:
tan ϕ−tan β
tan (ϕ − β) = (3.72)
1+ tan ϕ tan β
Sustituyendo por tan β como una función de tan ϕ hallamos:
n sin 2 ϕ
tan (ϕ − β) = (3.73)
1+ n cos 2 ϕ
Las expresiones cerradas que dan una función de (ϕ − ψ ) como una función ya sea de ϕ
o ψ , pueden deducirse en forma cerrada o en serie. Para deducir una expresión cerrada
escribimos:
33

43. tan ϕ − tan ψ
tan (ϕ − ψ) = (3.74)
1 + tan ϕ tan ψ
Sustituyendo (3.61) por tanψ podemos expresar:
e 2 sin 2 ϕ
tan (ϕ − ψ) = (3.75)
2 (1 − e2 sin 2 ϕ)
La derivación de expresiones en serie para las diferencias de dos latitudes puede ser
realizada usando (2.11) y (2.12). Por ejemplo, podemos aplicar esta técnica a la ecuación
(3.63) donde y = β, p = (1 − e 2 ) 1 / 2 y x=ϕ, encontramos:
n3
ϕ − β = n sin 2ϕ − n sin 4 ϕ + sin 6ϕ + ....
2
(3.76)
2 3
Esta diferencia, como una función de β podría escribirse:
ϕ − β = n sin 2β + n sin 4β + n sin 6β + ...
2 3
(3.77)
2 3
Usando un enfoque similar, la diferencia entre la latitud geodésica y geocéntrica como
una función de ϕ se escribe:
ϕ − ψ = m sin 2ϕ − m sin 4ϕ + m sin 6 ϕ + ...
2 3
(3.78)
2 3
Esta diferencia como una función de ψ es:
ϕ − ψ = m sin 2ψ + m sin 4ψ + m sin 6ψ + ...
2 3
(3.79)
2 3
Para el elipsoide de Clarke 1866 (f = 1/294,978698) tenemos (Adams, 1949):
ϕ − β = 350, 2202" sin 2ϕ − 0, 2973" sin 4ϕ + 0, 0003" sin 6ϕ + ...
34

44. (3.80)
ϕ − ψ = 700, 4385" sin 2ϕ − 1,1893" sin 4ϕ + 0, 0027" sin 6ϕ + ...
Para el elipsoide del Sistema de Referencia Geodésico 1980 tenemos:
ϕ − β = 350, 3640" sin 2ϕ − 0, 2908" sin 4ϕ + 0, 0003" sin 6ϕ
(3.81)
ϕ − ψ = 692, 7262" sin 2ϕ − 1,1632" sin 4ϕ + 0, 0026" sin 6ϕ
Podemos observar que la diferencia máxima de ϕ − β es aproximadamente 6’, mientras
que para ϕ − ψ la diferencia máxima es de 12’. Esta diferencia ocurre cerca de los 45º
de latitud.
3.5 Radios de Curvatura del Elips oide
Primero considere una normal a la superficie del elipsoide en algún punto. Ahora tome un
plano que contenga esta normal y sea así perpendicular al plano tangencial. Este plano
particular cortará la superficie del elipsoide formando una curva que se conoce como una
sección normal. Los radios de curvatura de una sección normal dependerán del acimut de
la línea. En cada punto existen dos secciones normales mutuamente perpendiculares
cuyas curvaturas son máximas y mínimas. Tales secciones se llaman secciones normales
principales.
En el elipsoide esas dos secciones normales son:
La sección meridiana está formada por un plano que pasa a través de un punto dado y los
dos polos;
La sección del primer vertical está formada por una sección que pasa a través del punto
dado y es perpendicular a la sección meridiana en el punto.
El radio de curvatura en el meridiano es designado M, y el radio de curvatura en el
primer vertical es designado N.
Con el objeto de encontrar el radio de curvatura en una dirección arbitraria podemos
utilizar la fórmula de Euler (ver Manual de Tablas y Fórmulas de Schaum, Relación de
Curvas Normales Geodésicas):
35

45. 1 cos 2 θ sin 2 θ
= + (3.82)
ρ ρ ρ
1 2
donde:
ρ es el radio de curvatura arbitrario;
θ es el ángulo medido desde la sección principal con el radio de curvatura más
grande ρ1 en una dirección normal principal; y
ρ2 es el radio de curvatura en la dirección de la otra dirección normal principal.
Después de examinar los valores de N y M aplicaremos la ecuación (3.82) al caso del
elipsoide.
3.5.1 Radio de Curvatura en el Meridiano
Primero consideramos la determinación de M. Recordemos que si se tiene una curva
plana especificada como z = F (x), el radio de curvatura en un punto sobre la curva es:
3/ 2
  dz  2 
1 +   
  dx  
ρ=  2
 (3.83)
d z
dx 2
De la ecuación (3.30) se tiene:
dz = − cot ϕ
dx
Luego diferenciando queda:
36

46. d 2z 1 dϕ 1 1
= = (3.84)
sin ϕ dx sin ϕ dx
2 2 2
dx
dϕ
De la ecuación (3.38) tenemos:
a cos ϕ
x=
1 − e 2 sin 2 ϕ
la que se diferencia con respecto a ϕ para obtener:
dx
=
(
− a 1 − e 2 sin ϕ )
( )
(3.85)
dϕ 1 − e 2 sin 2 ϕ 3 / 2
Reemplazando (3.85) en (3.84) tenemos:
(
d 2 z − 1 − e 2 sin 2 ϕ
=
) 3/ 2
dx 2 a sin 3 ϕ 1 − e 2 ( ) (3.86)
Sustituyendo los valores de (3.86) y de dz/dx dentro de (3.82) cuando ρ es ahora M,
encontramos:
M =
a 1 − e2( )
(1 − e )
(3.87)
sin ϕ
2 2 3/ 2
donde el signo menos ha sido eliminado por convención. Recordando las definiciones de
W, V, y c, las expresiones alternas para M son:
M =
(
a 1− e2 c
= 3
) (3.88)
3
W V
Ahora consideramos una deducción alterna para M tomando en cuenta la Figura 3.8:
37

47. z
ds
M
dϕ
x
Figura 3.8 Porción de un Arco de Meridiano
Tenemos ds, una distancia diferencial a lo largo de un arco de meridiano; dϕ es la
separación angular. Entonces consideramos M como el radio de curvatura del arco
meridiano, así:
ds = Md ϕ = dx 2 + dz 2 = dz 1 + ( dx ) 2 = dz 1 + tan 2 ϕ = dz (3.89)
dz cos ϕ
puesto que de la ecuación (3.30) tenemos:
dz = − cot ϕ
dx
Entonces:
38

48. dz
Mdϕ = cos ϕ
ó (3.90)
1 dz
M =
cos ϕ dϕ
Usando (3.39) hallamos para z:
dz = a(1−e2 ) cos ϕ (3.91)
dϕ W3
Lo que traduce (3.90) en
a(1−e2 )
M =
W3
que es lo mismo que (3.88)
En el ecuador ϕ = 0 así que:
( )
M ϕ =0 = a 1 − e 2 = a(1 − f )
2
(3.92)
En los polos ϕ = ± 90º por tanto:
M ϕ =90 o =
(
a 1−e2 ) =
a
=
a
=
a2
=c
(1 − e ) 2 3/ 2
1 − e2 1− f b
(3.93)
En esta expresión, c, el cual fue introducido previamente, es visto como el radio de
curvatura en el polo.
Podemos tomar la razón:
39

49. M 90 a
M 0 = 1− f ⋅ a (1− f )2 = (1− f )3
1 1
M0
M 90 = (3.94)
(1− f )3
Si los valores de M fuesen tabulados, ellos podrían trazarse con respecto a un origen en la
superficie del elipsoide de referencia. El punto extremo de los distintos valores M caería
en una curva según se muestra en el diagrama siguiente:
M90
∆2 M0
∆1
Figura 3.9 Radios de Curvatura de Meridianos Ecuatorial y Polar
Vamos a definir ∆ 1 y ∆ 2 según el diagrama:
Luego:
∆ 1 = a − a (1 − f ) 2 = a ( 2 f − f 2 ) = ae 2 (3.95)
Además
a( 2 f − f 2 ) ∆1
∆2 = a − b = = ae =
2
(3.96)
1− f (1− f ) (1− f ) (1− f )
40

50. Para el Sistema de Referencia Geodésico de 1980 tenemos los siguientes valores para
∆1 y ∆2 :
∆ 1 = 42,697.67 m
∆ 2 = 42,841.31 m
3.5.2 Radio de Curvatura en el Primer Vertical
Hay varios procedimientos para deducir N. Una idea es usar el teorema de Meusnier
donde el radio de curvatura ( de una sección inclinada es igual al radio de curvatura (N)
p)
de una sección normal, multiplicado por el coseno del ángulo (ϕ) entre esas secciones.
En nuestro caso deseamos hallar el radio de curvatura de la sección normal conociendo el
radio de curvatura de la sección inclinada. Tenemos:
Sección normal en el primer vertical
Radio de curvatura del primer vertical
Figura 3.10 Radio de Curvatura del Primer Vertical
41

51. Radio de curvatura del paralelo
p Sección normal en el primer vertical
Paralelo de latitud
N
ϕ
Figura 3.11 Geometría para el uso del Teorema de Meusnier
En la figura anterior, N es el largo de la línea normal desde la superficie del elipsoide
hasta la intersección de esta línea con el eje menor.
El radio de curvatura del paralelo es p. De la Figura 3.11:
p = N sin (90 − ϕ) = N cos ϕ (3.97)
El ángulo entre la sección del primer vertical y la sección inclinada es ϕ. Luego:
p = (radio de curvatura del primer vertical) × cosϕ
(3.98)
En las ecuaciones (3.97) y (3.98) vemos que el radio de curvatura en la dirección del
primer vertical es N.
Es posible un enfoque alterno a partir de un argumento geométrico. Para hacer esto
consideramos la figura siguiente, en la cual se ha dibujado una sección del primer
vertical:
42

52. P
Paralelo de Latitud
Sección del Primer Vertical
A B
Normal en A C
intersectando el eje
de rotación en H N
K
H
P1
Figura 3.12 Deducción Geométrica de N(A)
En esta figura, PAP1 representa el meridiano a través de A. AH es la normal en A,
intersectando al eje de rotación. B es un punto arbitrario en el mismo paralelo de A,
mientras que BH es la normal en B intersectando al eje de rotación en H. C es un punto
en la sección del primer vertical a través de A y que también yace en el meridiano que
pasa por B.
Construimos una normal en C que interseptará (en K) a la normal de A ya que AC es una
curva plana. Podemos decir que K es el centro aproximado de curvatura del arco AC.
Permítase ahora que el punto B se acerque al punto A, para que C se aproxime a A. La
intersección de las normales se acercará al verdadero centro de curvatura y CK se
aproximará al verdadero radio de curvatura del arco. Ahora, al acercarse C a A, C
también se aproxima a B para que K se acerque a H. Así que el radio de curvatura de la
sección del primer vertical en A tiene que ser la distancia desde H hasta A o AH. Para
calcular este radio consideramos la elipse meridiana en la figura siguiente.
43

53. N
ϕ
x
Figura 3.13 Deducción Geométrica de N (B)
De la figura tenemos:
x = N cos ϕ
Usando la expresión para x deducida previamente, podemos resolver para N y hallar:
a a c
N= = = (3.99)
1 − e sin ϕ
2 2 W V
En el ecuador el radio de curvatura del primer vertical es:
N ϕ =0 ° = a (3.100)
En el polo:
2
N ϕ =90° = a = a (3.101)
1− f b
44

54. Vemos que M (ver (3.92) y (3.39)) y N son mínimos en puntos sobre el ecuador. En el
polo M = N = a2 /b = c de ahí que ambas curvaturas sean las mismas.
Podemos hallar la razón de N/M usando las ecuaciones (3.88) y (3.99). Por tanto:
N c V3
M =V ⋅ c =V
2
ó
N
M = V = 1 + e' cos ϕ
2 2 2
(3.102)
Por tanto N ≥ M , donde la igualdad se manifiesta en los polos.
3.5.3 Radio de Curvatura de la Sección Normal en el Acimut α
Puesto que N generalmente es mayor que M, asociamos N con ρ1 que se presentó en la
ecuación (3.82). Si dejamos que α sea el acimut de una línea de la cual nos interesa
conocer su curvatura, tenemos θ = 90º−α . Si ρ = Rα podemos expresar la ecuación
(3.82) para el elipsoide de revolución de la manera siguiente.
1 = sin 2 α + cos2 α (3.103)
Rα N M
Rα = MN = N (3.104)
N cos2 α + M sin 2 α 1 + e'2 cos 2 α cos2 ϕ
3.6 Extensión de un Arco de Meridiano
Ahora pasamos a los cálculos de las extensiones de arcos de meridiano. En la ecuación
(3.89) se escribió una longitud de arco diferencial como:
45

55. ds = Mdϕ
Para descubrir la extensión de arco entre dos puntos con latitudes ϕ1 y ϕ2 se integra la
ecuación anterior para formular:
ϕ2 ϕ2 dϕ
s = ∫ Mdϕ = a (1 − e 2 ) ∫ (3.105)
ϕ1 ϕ1 W3
La integral
∫W
dϕ
3
( )
= ∫ 1 − e 2 sin 2 ϕ
−3 / 2
dϕ
representa una integral elíptica que no puede integrarse en funciones elementales. En su
lugar, el valor de 1 W 3 se desarrolla en series y la integración se efectúa término por
término. Primero veremos el desarrollo en serie de 1 W 3 de MacLaurin:
1
3
= 1 + 3 e 2 sin 2 ϕ + 15 e 4 sin 4 ϕ + 35 e 6 sin 6 ϕ + 315 e 8 sin 8 ϕ +693 e 10 sin 10 ϕ...
W 2 8 16 128 256
(3.106)
Para mayor facilidad en la integración reemplazamos las potencias de senϕ por
equivalentes de ángulo múltiple, según la ecuación (2.18), para encontrar:
1
= A − B cos 2ϕ + C cos 4ϕ − D cos 6 ϕ + E cos 8ϕ − F cos 8ϕ− F cos 10ϕ + ...
W3
(3.107)
donde los coeficientes A, B,...,F, tienen el significado siguiente:
A = 1 + 3 e 2 + 45 e 4 + 175 e 6 + 11025 e8 + 43659 e10 + ...
4 64 256 16384 65536
B= 3 e 2 + 15 e 4 + 525 e 6 + 2205 e8 + 72765 e10 + ...
4 16 512 2048 65536
46

56. C= 15 e 4 + 105 e 6 + 2205 e 8 + 10395 e 10 + ... (3.108)
64 256 4096 16384
D= 35 e 6 + 315 e 8 + 31185 e 10 + ...
512 2048 131072
E= 315 e 8 + 3465 e 10 + ...
16384 65536
F= 693 e10 + ...
131072
Ahora podemos sustituir (3.107) dentro de (3.105) y escribir:
s = a (1 − e 2 )∫ ( A − B cos 2ϕ − C cos 4ϕ)dϕ + − − −
ϕ2
ϕ1
s = a (1 − e 2 )∫ Adϕ − B ∫ cos 2ϕdϕ + C ∫ cos 4ϕdϕ + − − −
ϕ2 ϕ2 ϕ2
ϕ1 ϕ1 ϕ1
 ϕ2 ϕ2

( 2
)
ϕ2 B C
s = a 1 − e  Aϕ ϕ − sin 2ϕ + sin 4ϕ  + − − − (3.109)


1
2 ϕ1 4 ϕ1 

s = a (1 − e 2 )  A(ϕ2 − ϕ1 ) − B (sin 2ϕ2 − sin 2ϕ1 ) + C (sin 4ϕ2 − sin 4ϕ1 ) 

 2 4 

− D (sin 6ϕ2 − sin 6ϕ1 ) + E ( sin 8ϕ2 − sin 8ϕ1 ) − F (sin 10ϕ2 − sin 10ϕ1 ) + ... (3.110)
6 8 10
Esta ecuación puede ser escrita en una forma alterna usando la ecuación (2.22).
En este caso X = ϕ2 , Y = ϕ1, , de tal modo que:
 ϕ + ϕ2 
 sin (ϕ2 − ϕ1 )
n
sin nϕ2 − sin nϕ1 = 2 cos n  1 (3.111)
 2  2
haciendo:
47

57. ϕ1 + ϕ2
ϕm = y ∆ϕ = ϕ2 − ϕ1
2
podemos escribir valores específicos de (3.111) como:
sin 2ϕ2 − sin 2ϕ1 = 2 cos 2ϕm sin ∆ϕ
sin 4ϕ2 − sin 4ϕ1 = 2 cos 4ϕm sin 2∆ϕ (3.112)
sin 6ϕ2 − sin 6ϕ1 = 2 cos 6ϕm sin 3∆ϕ
y así seguidamente. La ecuación (3.112) podría entonces ser sustituida dentro de la
ecuación (3.110) quedando:
( )
s = a 1 − e 2 [ A∆ϕ − B cos 2ϕm sin ∆ϕ +
C D
cos 4ϕm sin 2∆ϕ − cos 6ϕm sin 3∆ϕ +
2 3 (3.113)
E F
cos 8ϕm sin 4∆ϕ − cos10ϕm sin 5∆ϕ + ...]
4 5
Con el propósito de calcular la longitud del arco de meridiano desde el ecuador hasta una
latitud arbitraria ϕ, igualaremos ϕ1 a cero y ϕ2 igual a ϕ en la ecuación (3.110). Entonces,
encontraremos (con s =Sϕ ):
( 
) B C D E F 
Sϕ = a 1 − e 2  Aϕ − sin 2ϕ + sin 4ϕ − sin 6ϕ + sin 8ϕ − sin 10ϕ + ... (3.114)
 2 4 6 8 10 
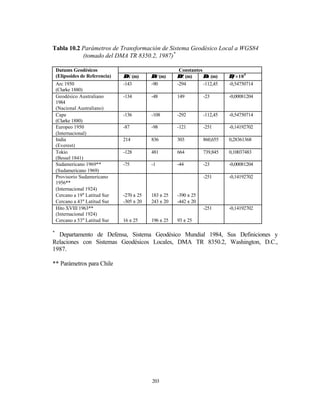
Helmert (1880) efectuó una deducción alterna para la longitud del arco meridiano en la
cual el parámetro de desarrollo es n en lugar de e2 . En este caso se obtiene una
convergencia más rápida de la serie. Tenemos:
Sϕ = a [a0 ϕ − a 2 sin 2ϕ + a4 sin 4ϕ − a6 sin 6ϕ + a8 sin 8ϕ ] (3.115)
1+ n
donde:
48

58. 2 4
a0 = 1 + n + n
4 64
3
a 2 = 3 (n − n )
2 8
4
a 4 = 15 (n 2 − n ) (3.116)
16 4
a 6 = 35 n 3
48
a 8 = 315 n 4
512
Para lograr una precisión de 0.1 mm en Sϕ desde el ecuador hasta el polo, es suficiente
dejar a8 en cero y omitir los términos de n4 en los coeficientes ai.
Usando la ecuación (3.114) ó (3.115) será fácil encontrar la distancia de arco desde el
ecuador hasta el polo haciendo ϕ =90º . De las ecuaciónes (3.114) y (3.115) tenemos:
π a ⋅ a0 π
( )
Sϕ = 90o = a 1 − e 2 A =
2 1+ n 2
(3.117)
Para el Sistema de Referencia Geodésico de 1980 (GRS80) tenemos las siguientes
constantes asociadas con el cálculo del arco de meridiano:
A = 1,00505250181
B = 0,00506310862
C = 0,00001062759
D = 0,00000002082
E = 0,00000000004 (3.118)
F = 0,00000000000
a0 = 1,00000070495
a2 = 0,00251882970
49

59. a4 = 0,00000264354
a6 = 0,00000000345
a8 = 0,00000000000
La evaluación de (3.117) da para el cuadrante del elipsoide del GRS80: 10.001.965,7293
m.
Para algunas aplicaciones conviene modificar las ecuaciones tales como (3.113), para
obtener ecuaciones válidas para líneas más cortas en extensión. Por tanto, sustituimos en
(3.113):
∆ϕ3
sin ∆ϕ = ∆ϕ −
6
sin 2 ∆ϕ = 2∆ϕ
Reteniendo los términos básicos de cos 4ϕm sin 2 ∆ϕ , pero haciendo aproximaciones
consistentes con el largo de las líneas para las cuales han de ser válidas las expresiones,
encontramos (Zakatov, 1962, pág. 27):
[
s = a∆ϕ 1 − ( 1 + 3 cos 2ϕm ) e 2 − ( 64 + 16 cos 2ϕm − 15 cos 4ϕm )e 4 + 1 e 2 ∆ϕ2 cos 2ϕm
4 4
3 3
64 8
]
(3.119)
La ecuación (3.119) es precisa para líneas con ∆ϕ = 5º (longitud = 556 km) en 0,03 m. Si
∆ϕ = 10º (longitud = 1100 km) el error es 0,07 m.
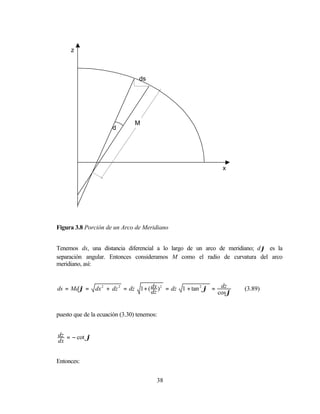
Para líneas aún más cortas pueden deducirse ecuaciones simplificadas. Si consentimos
que Mm sea el radio de curvatura del meridiano en la latitud media (p.ej., ϕm ) de la línea,
puede demostrarse que (Zakatov, pág. 27):
[
s = M m ∆ϕ 1 + 1 e 2 ∆ϕ 2 cos 2ϕm
8
] (3.120)
Para ∆ϕ = 5º , el error en esta ecuación es de 0,03 m. Para líneas inferiores a los 45 km.
de longitud, el término entre corchetes en (3.120) puede eliminarse de manera tal que
para esta distancia más corta queda:
50

60. s = M m ∆ϕ (3.121)
3.7 Extensión de un Arco de Paralelo
Ahora veremos los cálculos de la extensión del arco en el elipsoide entre dos p untos que
tienen longitudes λ1 y λ2 , situados en el mismo paralelo. La distancia L deseada se indica
en la Figura 3.14:
p
∆λ λ2
λ1 L
Figura 3.14 Extensión del Arco de un Paralelo
Recordemos de la ecuación (3.97) que la extensión del radio del paralelo ( es N cosϕ
p)
Así que de la figura:
L = p∆λ = N cos ϕ∆λ (3.122)
donde ∆λ está en radianes
51

61. 3.8 Cálculo de Áreas en la Superficie del Elipsoide
Deseamos considerar el área en el elipsoide limitada por meridianos y paralelos
conocidos. Para hacerlo, primero consideramos la figura diferencial siguiente:
dλ ϕ+ dϕ
C
B
ϕ
D
A
λ+ dλ
Ecuador
λ
Figura 3.15 Elemento de Área en el Elipsoide
De la figura diferencial ABCD tenemos:
AB = CD = Md ϕ
(3.123)
AD = BC = N cos ϕdλ
Dejando que el área de la figura diferencial sea dZ tenemos:
dZ = AD ⋅ AB = MN cos ϕdϕdλ (3.124)
El área entre meridianos designados por λ1 y λ2 , y paralelos designados por ϕ1 y ϕ2 , es:
52

62. ϕ2 λ2
Z = ∫ dz = ∫ ∫ MN cos ϕdϕdλ (3.125)
ϕ1 λ1
Integrando con respecto a λ tenemos:
Z = (λ2 − λ1 )∫ MN cos ϕdϕ
ϕ2
(3.126)
ϕ1
Para evaluar la integral sustituimos por MN para expresar:
ϕ2 ϕ2 cos ϕ
∫ϕ1
MN cos ϕdϕ = b 2 ∫
ϕ1
(1 − e 2
)
sin 2 ϕ
2
dϕ (3.127)
La integral que ocurre en (3.127) puede darse en forma cerrada como sigue (Bagratuni,
1967, pág. 59):
ϕ2
ϕ2 cos ϕdϕ b2  sin ϕ 1  1 + e sin ϕ 
b2 ∫ =  + ln   (3.128)
ϕ1
(
1 − e 2 sin 2 ϕ
2
2) 1 − e sin ϕ 2e  1 − e sin ϕ  ϕ1
2 2
Por tanto, la ecuación (3.126) podría escribirse:
( λ2 −λ1 )b2  sin ϕ  1 + e sin ϕ  ϕ 2
Z=  + 1 ln  
1 − e 2 sin 2 ϕ 2e  1 − e sin ϕ  ϕ 1
(3.129)
2
  
Como un caso especial de la ecuación (3.129), calculamos el área en el elipsoide desde el
ecuador hasta la latitud ϕ , completamente alrededor del elipsoide. Entonces (λ2 - λ1 ) =
2π, ϕ1 = 0 y ϕ2 = ϕ. La ecuación (3.129) se convierte en:
 sin ϕ 1  1 + e sin ϕ 
Z 0 −ϕ = π b 2  2 2 + 2e ln  
 1 − e sin ϕ  
(3.130)
 1−e sin ϕ 
Si nos interesa el área de la mitad del elipsoide, dejamos que ϕ = 90º en la ecuación
(3.130) para escribir:
53

63.   1 + e 
Z 0 −90 º = πb 2  1 2 + 1 ln 
1−e 2e  1 − e 
(3.131)
 
Para evaluar el área de todo el elipsoide, multiplíquese la ecuación (3.131) por dos.
En algunos casos puede ser más conveniente integrar la ecuación (3.127) usando una
expansión del núcleo en una serie, y su subsecuente integración término por término.
Primero escribimos:
cos ϕ
= cos ϕ + 2e 2 cos ϕsin 2 ϕ + 3e 4 cos ϕsin 4 ϕ + 4e 6 cos ϕsin 6 ϕ + ...
(1−e2 sin 2 ϕ) 2
(3.132)
La ecuación (3.132) puede ser usada en (3.127) la cual es empleada en (3.126) para
hallar:
[ 3 5
4 ]
Z = b 2 ( λ2 − λ1 ) sin ϕ + 2 e 2 sin 3 ϕ + 3 e 4 sin 5 ϕ+ 7 e 6 sin 7 ϕ+ ...
ϕ2
ϕ1
(3.133)
Si ( λ2 − λ1 ) = 2π y ϕ1 = 0º encontramos una ecuación de (3.133) correspondiendo a
(3.130) como:
[ 3 5
4
9 ]
Z 0 −ϕ = 2πb 2 sin ϕ + 2 e 2 sin 3 ϕ + 3 e 4 sin 5 ϕ+ 7 e 6 sin 7 ϕ + 5 e 8 sin 9 ϕ + ... (3.134)
El área total del elipsoide Σ , puede encontrarse dejando que ϕ = 90º en la ecuación
(3.134) y duplicando el resultado. Así encontramos:
∑ = 4πb 2 1 + 2 e 2 + 3 e 4 + 4 e 6 + 5 e 8 + 6 e10 + ...
 3  (3.135)
 5 7 9 11 
La ecuación (3.135) será útil en una sección próxima.
54

64. El área del elipsoide del GRS80 es 510.065.621,7 km2 .
3.9 Radio de Aproximación Esférica de la Tierra o Radio Medio de la Tierra
Como si ésta fuese una Esfera
En algunas aplicaciones conviene suponer que la Tierra es una esfera en vez de un
elipsoide. Se hace necesario, entonces, formular un radio adecuado, R, de la esfera para
su uso. Un radio apropiado puede definirse de varias maneras, a continuación se citan las
siguientes:
3.9.1 Radio Medio Gaussiano
El radio medio gaussiano se define como el valor integral medio de R tomado sobre el
acimut variando de 0º a 360º. Designando tal radio como R tenemos:
1 2π 1 2π MN
R=
2π ∫0 Rα dα = 2π ∫0 N cos 2 α + M sin 2 α dα (3.136)
M
2 2π
R = ∫0 cos 2 α (3.137)
π M
1+ tan 2 α
N
Removiendo MN la ecuación (3.137) puede escribirse como:
M dα
2 π/2 N cos 2 α
R= MN ∫ (3.138)
π 0
 M 
2
1+  tan α
 N 
 
Si admitimos t = ( M / N ) tanα, y se cambian los límites, la ecuación (3.138) podría
expresarse como:
55

65. 2 ∞ dt
R= MN ∫ (3.139)
π 0 1+ t 2
que en la integración produce:
a 1 − e2
R= MN = (3.140)
1 − e 2 sin 2 ϕ
3.9.2 Radio de una Esfera que tiene el Promedio de los Tres Semiejes del Elipsoide
Dejemos que:
Rm = a +a +b (3.140)
3
Sustituyendo por b y desarrollando, tenemos:
Rm = a  2 + 1−e  = a  2 + 1 1 − e + ... 
2 2
3 3  3 3   
   2 
Rm = a1 − e − e − e ...
2 4 6
 6 24 48 
(3.141)
 
3.9.3 Radio Esférico de la Esfera con igual Área que el Elipsoide
Para encontrar tal radio hacemos que el área de una esfera se iguale al área del elipsoide,
permitiendo que RA sea el radio de la esfera. Luego:
4π ⋅ R A 2 = Σ (3.142)
56

66. Despejando RA,
Σ
RA = (3.143)
4π
Usando la ecuación (3.135) hallamos:
 e 2 17 4 67 6 
R A = a 1 − −
 e − e + ... 
 (3.144)
 6 360 3024 
3.9.4 Radio de una Esfera con igual Volumen que el Elipsoide
El volumen de una esfera, VS se expresa como:
4
VS = π ⋅ Rv 3 (3.145)
3
donde R es el radio de la esfera. El volumen de un elipsoide se expresa como:
v
4
VE = π ⋅ a 2 b (3.146)
3
Igualando (3.145) y (3.146) hallamos:
Rv = 3 a 2 b (3.147)
Sustituyendo para b tenemos:
Rv = a (1 − e 2 )
1/6
(3.148)
57

67. (
Desarrollando 1 − e 2 )
1/ 6
dentro de una serie de MacLaurin, la ecuación (3.148) puede
expresarse como:
 e2 5 55 6 
Rv = a 1 −
 − e4 − e ... 
 (3.149)
 6 72 1296 
Para los parámetros del Sistema Geodésico de Referencia 1980 tenemos:
Rm = 6371008,7714 m
RA = 6371007,1810 m
Rν = 6371000,7900 m
Claramente la distinción entre estos radios es numéricamente pequeña. Para la mayoría
de las aplicaciones se puede usar 6371 km. Una técnica alterna para un radio esférico es
tomar el radio medio gausiano en una latitud específica.
3.10 Coordenadas Rectangulares Espaciales
Durante las explicaciones conectadas con la figura 3.3, definimos los ejes X, Y, Z. Ahora
consideramos el cálculo de las coordenadas X, Y, Z, de un punto ubicado en una altura
geométrica h, encima del elipsoide de referencia. La altura geométrica se mide a lo largo
de la normal al elipsoide. Para empezar consideremos la elipse del meridiano en la figura
3.16.
58

68. z
h
z’ z
x
ϕ
x
x’
Figura 3.16 Geometría de un Punto Localizado Fuera de una Elipse Meridiana
Tenemos:
x ' = x + h cos ϕ
(3.150)
z ' = z + h sin ϕ
donde x y z se conocen por las ecuaciones (3.42) y (3.44).
Las coordenadas rectangulares espaciales como se ven en la Figura 3.16 pueden
relacionarse a x’ y z’ como sigue:
X = x’ cos λ
Y = x’ sin λ (3.151)
Z = z’
59

69. Usando las ecuaciones (3.42) y (3.43) y la expresión para x’ y z’, se ontiene:
X = (N + h) cosϕ cos λ
Y = (N + h) cosϕ sinλ (3.152)
Z = (N (1-e2 ) + h)sinϕ
Donde N = a/W. Un problema que se tratará más adelante, es el cálculo de ϕ , λ , y h
conociendo las coordenadas rectangulares espaciales X, Y, Z.
3.11 Una Forma Alterna para la Ecuación del Elipsoide
Previamente escribimos la ecuación de una elipse (ver ecuación 3.23) de la forma:
x2 + z 2 = 1
a2 b2
donde x es la coordenada medida paralela al semieje mayor y z se mide paralela al
semieje menor. La ecuación del elipsoide puede escribirse de una manera semejante:
X 2 + Y2 + Z2 =1 (3.153)
a2 a 2 b2
en donde X, Y, Z son las coordenadas rectangulares espaciales para los puntos sobre el
elipsoide.
Una forma alterna a (3.153) fue descrita por Tobey (1928). Primero definimos los ejes
x’, y’, y z’ en un punto P sobre la superficie del elipsoide. x’ es tangente al elipsoide
hacia el polo, y’ es tangente al elipsoide en dirección Este y z’ es normal al elipsoide,
positiva hacia el centro. Este sistema se muestra en la Figura 3.17.
60

70. S x’
y’
T P
z’
N
Q
90°-ϕ
nP
Figura 3.17 Sistema Local de Coordenadas en el Elipsoide
Usando la anotación de Tobey, indicamos la sección meridiana de la elipse como SPQ.
La normal de P al eje menor es el radio de curvatura del primer vertical N, y ϕ es la
latitud geodésica del punto P.
Defina una esfera de radio N que tiene su centro en nP y, por tanto, es tangente al
elipsoide en P y a todos los puntos en el paralelo PT. La ecuación de este círculo en el
plano del meridiano es:
x’2 + z’2 - 2Nz’ = 0 (3.154)
donde el origen está en P. La ecuación correspondiente para la esfera tangente sería:
x '2 + y '2 + z ' 2 − 2 Nz ' = 0 (3.155)
61

71. La elipse meridiana es la curva que es tangente en P donde la línea x ' cos ϕ − z ' sin ϕ = 0
corta el círculo x '2 + z '2 − 2 N z ' = 0 . Por tanto, la ecuación de la elipse meridiana en
este sistema local de coordenadas toma la forma:
x '2 + z '2 − 2 Nz ' + δ ( x ' cos ϕ − z ' sin ϕ) 2 = 0 (3.156)
Una ecuación de elipsoide debe reducirse a (3.156) cuando y’ = 0. Así la ecuación
general para un elipsoide podría escribirse como:
x '2 + z '2 − 2 Nz ' + δ ( x ' cos ϕ − z ' sin ϕ) 2 + f ( y ' ) = 0 (3.157)
Permitiendo que δ = 0, y comparando (3.157) con (3.155), tenemos f (y’) = y’2 , para que
la ecuación del elipsoide sea:
x '2 + y '2 + z '2 − 2 Nz ' + δ ( x ' cos ϕ − z ' sin ϕ) 2 = 0 (3.158)
Tobey (idem. Proposición I) demuestra que δ = e'2 lo cual fue definido previamente. La
ecuación (3.158) se considera como una forma alterna a (3.153) para la ecuación del
elipsoide de rotación.
62

72. 4 CURVAS EN LA SUPERFICIE DEL ELIPSOIDE
4.1 Secciones Normales
4.1.1 Introducción
Hemos definido previamente una sección normal como una curva formada por la
intersección de un plano que contiene la normal en un punto dado en la superficie del
elipsoide. Una sección normal específica desde el punto A al punto B está formada por la
intersección de un plano, que contiene la normal en el punto A que pasa a través del
punto B, con la superficie del elipsoide de referencia.
Físicamente, la sección normal puede ser vista cuando se nivela un teodolito con respecto
a la normal del elipsoide en el punto donde se encuentra el instrumento. Un plano normal
es el plano que se genera al mover el telescopio en dirección vertical. Visualizando un
objeto distante, definimos un plano que contiene la normal en el sitio de observación, y
que pasa a través del sitio observado. La intersección de este plano con el elipsoide forma
la sección normal desde el punto de observación hasta el punto observado.
En la figura siguiente se muestran las secciones normales desde A hasta B, y luego desde
B hasta A, notando que, en general, tales secciones son diferentes debido a que las
normales al elipsoide en latitudes distintas, intersecan el eje menor en lugares diferentes.
Las dos secciones diferentes algunas veces son llamadas secciones contra-normales.
63

73. B
0
A
nA
nB
Las distancias OnA y OnB pueden ser calculadas considerando el diagrama siguiente, que
es una sección meridiana a través de A.
A
zA NA
ϕ O
nA
Figura 4.1 Determinación de la Distancia On A
64

74. Tenemos:
On A = N A sin ϕA − z A (4.1)
Usando la ecuación (3.39) para z tenemos:
On A = N A sin ϕA − N A (1 − e 2 ) sin ϕA = e 2 N A sin ϕA (4.2)
Similarmente:
On B = e 2 N B sin ϕB (4.3)
Si ϕA 〉 ϕB ; On A > On B se deduce que mientras más al norte esté la ubicación del punto a
través del cual se pasa la normal, mayor será On y más distante hacia el sur estará el eje
de rotación intersecado por la normal. Así que si A se halla al sur de B, la sección normal
desde A hacia B se encontrará al sur de la sección normal desde B hacia A.
En general, el hecho de tener dos secciones normales entre dos puntos crea problemas
cuando se usan observaciones de dirección en los cálculos. Esto puede verse en la figura
siguiente, donde las líneas observadas se indican para un triángulo en la superficie del
elipsoide.
θ3
θ1
θ2
Figura 4.2 Un “Triángulo” de Sección Normal
Los ángulos medidos son θ1 , θ2 , y θ3 . A simple vista podemos concluir que no se ha
observado ninguna figura cerrada.
65

75. Finalmente, vamos a considerar dos casos en donde sólo hay una sección normal entre
dos puntos. El primero ocurre cuando los dos puntos están en un meridiano. El segundo,
cuando los dos puntos están en el mismo paralelo. El primer caso ocurre porque el
meridiano es una curva plana, mientras que el segundo está claro porque las normales en
la misma latitud interceptan al eje menor en el mismo punto.
4.1.2 Separación entre Secciones Normales Recíprocas
Estamos interesados en las diferencias acimutales y distancias entre secciones normales
recíprocas. Antes de considerar esas cantidades deduciremos una expresión para el
ángulo f, que es el ángulo entre los planos generados por las secciones normales entre A y
B. Este ángulo se muestra en la figura 4.3.
Sección Normal desde B hasta A B
f
Cuerda conectando A y B
Sección Normal desde A hasta B
A
Figura 4.3 Ángulo entre las Secciones Normales Recíprocas en la Cuerda que las
Conecta
Para encontrar este ángulo consideramos la Figura 4.4.
66

76. Polo
360°-αBA
B
αBA
f 90-σ/2
αAB
A
δ2
Semieje
f Menor
n’ A
360°-αBA b
n’ B
σ
nA
90 + ϕB - δ2
90-ϕB
nB
Figura 4.4 Geometría de la Sección Normal
67

77. El ángulo αAB es el acimut de la sección normal desde A hacia B en A, mientras que αBA
es el acimut de la sección normal desde B hacia A en B. σ es el ángulo entre las líneas
rectas nAA y nBB. δ2 es el ángulo nABnB. BnAnB yace en el plano meridiano a través de B.
Puesto que An A ≈ Bn A , el triángulo AnAB es aproximadamente un triángulo isósceles.
Por tanto, el ángulo ABnA es aproximadamente 90º - σ/2
Luego construimos los arcos A A’ y AnB’, desde el punto B como centro. El arco n A ' n B '
n
estará en el meridiano a través de B y será de longitud δ2 . Consecuentemente, el ángulo
interior n A ' nB ' A será de 360º - αBA. El arco AnA ' será de 90º - σ/2.
El ángulo n A ' AnB ' será igual al ángulo f que queremos evaluar. Aplicando la ley de senos
al triángulo AnA ' nB ' , tenemos:
sin f sin (360 º − αBA )
= (4.4)
sin δ2
sin (90º − σ
2
o resolviendo para sin f
− sin δ2 ⋅ sin αBA
sin f = (4.5)
sin ( 90º − σ)
2
Del triángulo plano Bn A nB tenemos:
sin δ2 sin( 90º + ϕB − δ2 )
nA nB = Bn
(4.6)
B
donde ϕB es la latitud del punto B. Para encontrar nAnB restamos (4.2) de (4.3).
n A n B = On B − On A = e 2 ( N B sin ϕB − N A sin ϕA ) (4.7)
Sustituyendo N y omitiendo los términos en el orden de ae4 (ϕA-ϕB) encontramos:
n A n B = ae 2 (ϕB − ϕA ) cos ϕm (4.8)
donde ϕm es la latitud media.
Expandiendo la expresión de ángulos múltiples de (4.6) tenemos:
68

78. n A nB n n
sin δ2 = cos ϕB cos δ2 + sin ϕB A B sin δ2 (4.9)
Bn B Bn B
Sustituyendo (4.8) dentro de (4.9), omitiendo los términos extremos del lado derecho, y
notando que BnB = NB tenemos:
ae 2 (ϕB − ϕA ) cos ϕB cos ϕm
sin δ2 = (4.10)
NB
Con un error de e 4 (ϕB − ϕA ) tomamos a/N B igual a uno y escribimos:
sin δ2 = e 2 (ϕB − ϕA ) cos ϕB cos ϕm (4.11)
Jordan (1962) dio una expresión cerrada para determinar δ 2 y una forma en serie más
exacta que (4.11). La forma cerrada es Jordan (idem, Volumen III, 2, pág. 3):
 V 
e 2  sin ϕB − sin ϕA B  cos ϕB
 VA 
tan δ2 = (4.12)
 V 
1 − e 2  sin ϕB − sin ϕA B  sin ϕB
 VA 
La forma de la serie es (idem, p.3):
∆ϕ ηB 2 t B ∆ϕ2 ηB 2 ∆ϕ3 ηB 2 t B ∆ϕ4
δ 2 = ηB + − − + −−−
2
2
(4.13)
VB 2 VB 4 6 VB6 24 VB 8
donde η2 = e' 2 cos 2 ϕ y t = tan ϕ (4.14)
Sustituyendo (4.11) dentro de (4.5) tenemos:
− e 2 (ϕB − ϕA ) cos 2 ϕm sin αBA
sin f = (4.15)
σ
cos
2
donde suponemos que ϕB = ϕm .
Para encontrar σ consideramos una aproximación de suficiente precisión. Tomamos un
triángulo esférico pequeño, según la Figura 4.5:
69

79. Meridiano
Paralelo
B
(ϕβ - ϕA )
s
Aproximación a la Sección Normal
σ
αAB
A
Figura 4.5 Una Aproximación Para el Arco Esférico σ
Del triángulo tenemos aproximadamente:
(ϕB − ϕA ) = σ cos αAB (4.16)
Suponiendo que α21 = α12 ± 180 º (esto es, ignorando la convergencia meridiana en
consideración a que estamos tratando con líneas de un largo de 50-100 km), permitiendo
σ
que cos ≈ 1, f ≈ sin f y sustituyendo la ecuación (4.16) dentro de (4.15), encontramos:
2
1 2
f = e σ cos 2 ϕm sin 2αAB (4.17)
2
Una aproximación razonable para σ es s/N A, donde s es la dimensión de la sección
normal. Entonces:
1 2 s
f = e cos 2 ϕm sin 2αAB (4.18)
2 NA
70

80. De (4.18) vemos que f aumenta linealmente con la distancia. Se reducirá al aumentar la
latitud y será un máximo para líneas que tengan por acimut múltiplos impares de 45º.
Para s = 100 km, ϕm = 45o y α12 = 45º, f = 5,4”.
4.1.3 Separación Lineal de Secciones Normales Recíprocas
Ahora consideramos la separación lineal entre las secciones normales. Veamos la
siguiente figura, donde, con suficiente exactitud los arcos AaB y AbB pueden tomarse
como arcos esféricos con centros en nA y nB.
B
b Eje menor
k2 k
f
k1
a
90 -σ/ 2
90 -θ / 2
A
θ σ
nA
nB
Figura 4.6 Geometría de la Separación Lineal de la Sección Normal
71

81. El punto k es un punto arbitrario en la sección normal de A a B, θ es el ángulo, análogo a
σ , knAA. Como k varía en posición entre A y B, θ varía de 0 a σ. Tenemos:
Ángulo BAnA = 90º - σ (4.19)
2
Ángulo kAnA= 90º - θ
2
Ángulo kAB = kAnA - BanA = σ−θ (4.20)
2
De la figura 4.6 tenemos:
θ
Ak = 2 N A sin (4.21)
2
Ahora consideremos un triángulo cuyo vértice está en la cuerda:
d Arco en la Superficie
del Elipsoide
k2 k
f
k1
Figura 4.7 Separación Lineal
De la Figura 4.7 tenemos:
kk 2 = d = kk1 ⋅ f (4.22)
donde d es la separación lineal deseada. También usando (4.20) y (4.21), tenemos:
kk1 = Ak sin kAB = 2 N A sin θ sin σ2 θ
− (4.23)
2
Usando las ecuaciones (4.18) y (4.23) en (4.22) encontramos:
72

82. θ σ−θ
d = e 2 s sin sin 2 cos 2 ϕm sin 2αAB (4.24)
2
Suponiendo que σ y θ son pequeños, la ecuación (4.24) podrá escribirse:
d = e s θ(σ − θ) cos 2 ϕm sin 2αAB
2
(4.25)
4
La separación máxima ocurrirá enθ = σ , que al sustituirse dentro de la ecuación (4.25)
2
produce:
e2
d max = 16 sσ 2 cos 2 ϕm sin 2αAB (4.26)
o al sustituir para σ :
d max = 16 s 2 cos 2 ϕm sin 2αAB
e2 3 (4.27)
NA
La ecuación (4.27) falla en principio cuando los dos puntos están ubicados en el mismo
paralelo, ya que la separación d debiera ser cero en este caso. Sin embargo, el resultado
será correcto dentro de la precisión de la derivación. Una fórmula más exacta es
determinada por Zakatov (1962, pág. 53):
2σ3 σ
d max = N A e 8 sin αAB cos 2 ϕA (cos αAB − tan ϕA ) (4.28)
2
Ejemplos numéricos usando 4.27:
Caso 1 ϕm = 45º , αAB = 45º
s 200 km 100 km 50 km
d max (m) 0,050 m 0,006 m 0,0008 m
Caso 2 ϕm = 52º , αAB = 45º
s 150 km 100 km 20 km
d max (m) 0,013 m 0,0038 m 0,0001 m
Evidentemente esta separación lineal es muy pequeña y no tiene ningún significado
práctico.
73

83. 4.1.4 Separación Acimutal de una Sección Normal Recíproca
Designamos el ángulo entre las secciones normales, medido tangente a las secciones
normales como ∆ . Este ángulo también es la diferencia entre los acimut de las dos
secciones normales, como puede verse a continuación:
Polo
B
α’ AB
∆
αAB
A
Figura 4.8 Separación Acimutal de la Sección Normal
Tenemos:
∆ = αAB − α' AB (4.29)
donde α' AB es el acimut de la sección normal desde B hasta A en el punto A.
De la Figura 4.6 escribimos:
kk2
Ángulo kAk2 = (4.30)
Ak
o usando (4.25) para kk 2 y dejando que Ak = N Aθ tenemos:
e2 s (σ−θ)
Ángulo kAk2 = 4 N A cos ϕm sin 2αAB
2
(4.31)
74

84. = e σ(σ − θ) cos 2 ϕm sin 2αAB
2
4
Para obtener el ángulo ∆ , permitimos que θ tienda a cero de modo que el ángulo kak 2 ,
en el límite, tienda al ángulo deseado. Entonces tenemos:
e2 σ2 cos2 ϕm sin 2αAB e2 s 2
∆= = 4 ( N ) cos 2 ϕm sin 2αAB (4.32)
4 A
Nótese que (4.32) se divide cuando los dos puntos están en el mismo paralelo al igual que
(4.27). En este caso se necesita una expresión más precisa para ∆. De Jordan (Vol. III, 2da
mitad, pág. 16) tenemos:
tan ϕ s
∆ = e sin αAB ( N ) 2 cos 2 ϕA (cos αAB − 2 A N )
s
2
(4.33)
2 A A
Uno puede mostrar que la expresión de más a la derecha en (4.33) es esencialmente cero
para puntos cercanos al mismo paralelo.
Ejemplo de valores de ∆ calculados de (4.33) se muestran a continuación:
Caso 1 ϕA = 0º , αAB = 45º
s 200 km 100 km 50 km
∆" 0,339 m 0,085 m 0,021 m
Caso 2 ϕA = 52º , αAB = 45º
s 150 km 100 km 30 km
∆" 0,071 m 0,032 m 0,003 m
Generalmente, para distancias de hasta 20-25 km no es necesario considerar la separación
angular de las secciones normales. Para distancias mayores, normalmente es necesario
hacer las correcciones apropiadas usando ecuaciones tales como (4.33).
75

85. 4.1.5 El Arco Elíptico de una Sección Normal
Durante la deducción en la sección anterior, en varios casos intercambiamos σ y (s/N A).
Es apropiado considerar una relación más rigurosa entre σ y s. Primero veremos la
Figura 4.9
αAB B
A s
S2
NA
σ
nA
Figura 4.9 Arco Elíptico de una Sección Normal
Tenemos s, la distancia de la sección normal; σ el ángulo AnAB, y S2 la distancia nAB.
da
Después de alguna manipulación, se puede mostrar (Jordan, pág. 11, Vol. III, 2 mitad)
que:
S2 1 1
= 1 − σ 2 ηA cos 2 αAB + σ 3η2 t A cos αAB + − − −
2
(4.34)
NA 2 2
donde:
ηA 2 = e ' cos 2 ϕA
t A = tan ϕA
Ahora deseamos calcular una distancia diferencial ds a lo largo del arco de la sección
normal. Para hacerlo, consideremos la Figura 4.10:
76

86. ds
B
A
S2
NA dσ
σ
Figura 4.10 El Elemento Diferencial en el Arco Elíptico
Tenemos:
ds 2 = ( S 2 dσ ) 2 + ( dS 2 ) 2 (4.35)
El primer término puede escribirse de (4.34) como (se omiten los subscritos A y AB para
mayor conveniencia):
1 1 1
(S2 dσ) 2 = N 2 (1 −σ2η2 cos2 α + σ3η2t cosα+ σ4η4 cos4 α− σ5η4 t cos3 α+ σ6η4 t 2 cos2 α)dσ2
4 2 4
(4.36)
Luego diferenciamos (4.34) considerando a σ como la variable. Elevando al cuadrado el
resultado se obtiene:
( dS 2 ) 2 = N 2 (η4 cos 4 ασ 2 − 3η4 t cos 3 ασ 3 + 9
4
η4 t 2 cos 2 ασ 4 ) dσ 2 + − − − (4.37)
Tomando la raíz cuadrada de la suma representada por (4.35) queda:
ds =  N + Nη2 cos 2 α (η2 cos 2 α)σ 2 − N η2 cos 2 ασ 2 + N η2 t cos ασ 3 − 3 2 η4 t cos 3 ασ 3  dσ
1 N
 

2 2
2 
(4.38)
Ahora integramos esta expresión de 0 a s, y correspondientemente de 0 a σ para hallar:
s = N A σ 1 + σ 2η2 cos 2 αAB (η2 cos 2 αAB − 1 ) + η2 t A cos αAB (1 − 3η2 cos 2 αAB )σ 3 
1 1
 6 A A A A 
 8 
(4.39)
Usando (2.10) podemos invertir esta ecuación para obtener:
77

87. s  1 2 
2 3
 s  1 2  s 
σ= 1 + ηA cos αAB (1 − ηA cos αAB )
2 2 2

2
(
 N  − 8 ηA t A cos AB 1 − 3ηA cos αAB
2
)
N  + ...
NA  6  A  A 
 
(4.40)
4.1.6 Corrección del Acimut debido a la Altura del Punto Observado
Cuando las direcciones son medidas, como por ejemplo con teodolitos, éstas medidas son
entre puntos ubicados sobre la superficie de la Tierra. No obstante, generalmente los
cálculos geodésicos se efectúan en la superficie del elipsoide de referencia. Por lo tanto
es necesario corregir las observaciones, donde sea apropiado, por cualquier efecto
causado al pasar desde la superficie terrestre al elipsoide de referencia. Un efecto
considerado en esta sección es aquél causado por la altura del punto que está siendo
observado.
Para considerar este efecto, se ubica un punto A en el elipsoide de referencia y un punto B
en una elevación h. Nivelamos el teodolito en A y pasamos un plano, normal en A, a
través del punto elevado B. El acimut de A podría ser designado como αh . No obstante,
este acimut no es el deseado, ya que el que se requiere es uno hacia el punto b proyectado
sobre el elipsoide de referencia. Dejemos que este acimut sea α. Puesto que el elipsoide
se encuentra ligeramente achatado, la diferencia (α-αh ) que ha de ser determinada, es
pequeña.
Para calcular esta diferencia consideramos la figura siguiente:
B
αh h
b’
α
b
A δ2
nA
nB
Figura 4.11 Efecto Acimutal para un Punto Elevado sobre el Elipsoide
78

88. La proyección de b sobre el elipsoide queda determinada por la normal al elipsoide que
pasa a través de B. El punto b’ es un punto en el elipsoide determinado por la intersección
del plano normal en A que pasa a través de B, con el meridiano de b. El ángulo δ2 es el
ángulo nABnB. Con suficiente exactitud, podemos asociar δ2 con δ2 indicado en la
ecuación (4.11). Con este propósito escribimos la ecuación (4.11) en la forma:
δ2 ≈ e 2 ∆ϕ cos2 ϕm (4.41)
donde ∆ϕ es la diferencia en latitud (ϕB - ϕA). Ahora volvemos a escribir (4.16) dejando,
con suficiente exactitud, que σ = s / M m , donde Mm es el radio de curvatura del meridiano
en la latitud media ϕm . Tenemos entonces:
s
∆ϕ = M cos αAB (4.42)
m
lo cual podría ser sustituido dentro de (4.41) para obtener:
s
δ 2 = M e 2 cos 2 ϕm cos αAB (4.43)
m
El arco bb’ es entonces hδ2 así que:
hs
bb' = M e 2 cos 2 ϕm cos αAB (4.44)
m
Consideramos de inmediato el triángulo b’Ab.
b’
αh 360-αBA
α-αh b
α
A
Figura 4.12 Triángulo Pequeño para la Determinación del Efecto de Altura.
79

89. Aplicamos la ley de senos para escribir (asumiendo una figura plana ya que tratamos con
triángulos relativamente pequeños en el elipsoide):
sin( α −αh ) sin( 360º − αBA )
= s (4.45)
bb'
Sustituyendo (4.44) dentro de (4.42) y dejando que:
sin( α − αh ) ≈ α − αh
sin( 360º−αBA ) ≈ sin αAB
encontramos:
h
α − αh = 2 M e 2 cos 2 ϕm sin 2αAB (4.46)
m
La ecuación (4.46) entrega la corrección deseada. Por tanto, el acimut corregido α
obtenido del acimut medido es:
h
α = αh + 2 M e 2 cos 2 ϕm sin 2αAB (4.47)
m
Una expresión más exacta para α-αh se halla en Jordan (III, 2da parte, pág. 20) como:
h s
α − αh = N η2 (sin αAB cos αAB − 2 N sin αAB tan ϕA ) (4.48)
A
A A
Advertimos que para una primera aproximación, la corrección que está calculándose no
depende de la separación de los dos puntos. Además, si la excentricidad del elipsoide es
cero, la corrección es cero. Por lo cual, la corrección no existiría para una esfera. En
realidad, la razón principal por la que existe la corrección se debe a que las normales del
elipsoide en diferentes latitudes interceptan el eje menor en ubicaciones distintas.
Consideramos dos cálculos numéricos:
Si ϕm = 45º , h = 1000 m, α − αh ≤ 0,05" ; para h = 200m, α − αh ≤ 0,008"
Jordan (III, 2da parte, pág. 20) da el siguiente ejemplo para una línea medida desde
España hasta África del Norte:
80

90. ϕ1 = 35º 01'
αAB = 327º 40'
h = 3.482 m
s = 269.926 m
Entonces evaluando la ecuación (4.48) se encuentra que:
α −αh = − 0, 2291" + 0,0040" = − 0,2251"
Esta corrección de altura siempre deberá considerarse al reducir observaciones, aunque
en general sólo es apropiada para elevaciones más altas. Sin embargo, si se descuidara la
corrección en elevaciones bajas, podría causar errores sistemáticos al efectuarse los
cálculos de la triangulación.
Finalmente, recordamos que en nuestras deducciones asumimos que el punto A estaba
localizado sobre la superficie del elipsoide de referencia. Si el punto A estuviera elevado,
nuestro argumento no se alteraría puesto que las direcciones en A se miden con respecto a
la normal en A. Así que la corrección α − αh no depende de la altura de la estación de
observación.
4.1.7 El Ángulo de Declinación de la Cuerda
Considérense dos puntos A y B en el elipsoide que están conectados por una curva de
sección normal de largo s. Permítase que sea µ el ángulo de inclinación con respecto a la
tangente en A, en la dirección AB, según la Figura 4.13.
A µ
c
B
NA
S2
σ
Figura 4.13 El Ángulo de Declinación de la Cuerda
81

91. El ángulo de declinación µ se mide, en esta derivación, positivo hacia abajo.
De la Figura 4.13 tenemos:
S2 sin σ
tan( 90 º − µ) = N − S cos σ (4.49)
A 2
o
N
tan µ sin σ = A − cos σ (4.50)
S2
Podemos rescribir (4.50) usando NA/S2 determinado de (4.34) y luego expandiendo en
serie tan µ, sin σ, y cos σ . Tenemos (Jordan, III, 2da parte, pág. 12):
1 1
µ= σ(1 + ηA cos 2 αAB ) − σ 2ηA t A cos αAB
2 2
(4.51)
2 2
Si queremos una expresión para µ en términos de s, usamos (4.40) para escribir:
s s
µ= (1 + η2 cos 2 αAB ) −
A 2
η2 t A cos αAB
A (4.52)
2N A 2N A
Consideramos algunos valores numéricos de µ al tomar un punto donde
ϕA = 45º , y αAB = 45 º. Para este caso tenemos:
s (km) µ
10 2’ 41,7”
30 8’ 5,09”
50 13’ 28,5”
75 20’ 12,7”
100 26’ 56,9”
4.1.8 La Sección Normal y la Magnitud de la Cuerda
Dejemos que la extensión de la cuerda entre AB sea c, según la Figura 4.13. Escribimos
(Jordan, III, 2da parte, pág. 12):
c sin σ sin σ
NA = sin ( µ+90 º−σ) = cos (σ−µ) (4.53)
Ya que σ es pequeña, podemos expandir el lado derecho de (4.53):
82

92. c = σ (1 − σ 2 + σ4 ) (1 + 1 (σ − µ) 2 + 5 (σ − µ) 4 ...) (4.54)
NA 6 120 2 24
Podemos obtener una expresión para σ − µ de (4.51) para que (4.54) se pueda escribir
como:
c  1
(
2 1
)
= σ 1 − σ 2 1 + 6ηA cos 2 αAB + σ 3ηA t A cos αAB +
2 1 
σ 4 ... (4.55)
NA  24 4 1920 
Si introducimos (4.40) hallamos:

c = s 1 −
1 s2
24 N A 2
( )
1 + 2ηA 2 cos 2 αAB +
1 s3
8 N A3
ηA 2 t A cos αAB +
1 s4 
 (4.56)
1920 N A 4 

La ecuación (4.56) puede invertirse usando (2.10) para hallar la distancia de la sección
normal conociendo la distancia de la cuerda. Encontramos:

c = s 1 −
1 c2
2
(
1 + 2ηA 2 cos 2 αAB −)1 c3
8 N A3
ηA 2 t A cos αAB +
3 c4 

640 N A 4 
 24 N A
(4.57)
Bagratuni (1967, pág. 77) da una fórmula más exacta para obtener la distancia de la
sección normal, como sigue:
 1  c 6 
 1 +   + 3  c  + 5  c  + µ1  c  + 3 µ2  c  + − − − 
4 6 8 4
s=c        
 6  2r  40  2r  112  2r  2  2r  5  2r  
 
(4.58)
donde:
r 2 = x12 + y12 + z 12 , es el radio geodésico al primer punto.
e'2 sin 2ϕA cos αAB
µ1 =
1 + ηA 2 cos 2 αAB
(4.59)
µ2 =
2
(
e' sin 2ϕA − cos ϕA cos αAB
2 2
)
1 + ηA 2 cos 2 αAB
La exactitud de estas fórmulas depende principalmente del largo de la línea. Por ejemplo,
el último término en (4.57) multiplicado por c tiene un valor de 9 mm con c = 200 km, y
68 mm para c = 300 km.
83

93. 4.1.9 La Sección Normal en un Sistema de Coordenadas Local
Consideremos dos puntos A y B ubicados en o encima de la superficie del elipsoide. Las
coordenadas rectangulares espaciales de estos dos puntos pueden determinarse de la
ecuación (3.152), suponiendo que conocemos la latitud, longitud y altura de cada punto
sobre el elipsoide.
Ahora introducimos un sistema de coordenadas local u, v, w donde el origen para este
sistema está en el punto A. El eje w está en la dirección de la normal al elipsoide en el
punto A. El eje u es perpendicular al eje w en la dirección norte definida por el meridiano
geodésico. El eje v es perpendicular al plano u-w apuntando en dirección Este, positiva.
Dichos ejes se muestran en la Figura 4.14.
Z
w
u
v
A B
hA
Y
λA ϕA ϕB
λB
X
Figura 4.14 Sistemas de Coordenadas Local y Rectangular Espacial
El sistema de coordenadas local puede ser visto también en término de “observaciones”
de la distancia de la cuerda, c, el ángulo vertical, V, y el acimut de la sección normal, α,
desde A hacia B, como es mostrado en la Figura 4.15.
84

94. w
u
B
c
V
α
A v
Figura 4.15 El Sistema de Coordenadas Local.
Observe que el plano uv forma el plano horizontal geodésico. El ángulo vertical, V, puede
ser considerado como una generalización del ángulo de declinación de la cuerda, µ,
descrito en la sección 4.17, aunque con signo contrario. Note que, con la dirección
escogida para v, se forma un sistema coordenado de mano izquierda puesto que u es
considerado el eje primario, v el secundario y w el terciario. Si v fuese escogido en la
dirección opuesta, el sistema podría ser de mano derecha.
De la Figura 4.15 podemos determinar las coordenadas u, v, w a partir de α, V, y c, como
sigue:
u = c cos V cos α
v = c cos V sin α (4.60)
w = c sin V
Dividiendo las dos primeras ecuaciones tenemos:
v
tanα = u (4.61)
donde notamos de nuevo que α es un acimut de la sección normal.
Ahora deseamos expresar las coordenadas locales en términos de diferencias con las
coordenadas rectangulares espaciales (∆X = XB - XA; ∆Y = YB - YA; ∆Z = ZB - ZA. Para
hacerlo, primero trasladamos los ejes X, Y, Z a un juego paralelo de ejes cuyo origen está
en el punto A, según la Figura 4.16:
85

95. Z
w v
u
90°-ϕ
u’
180°-λ Y
A
X
Figura 4.16 Traslado del Origen de los Ejes X, Y, Z al Punto A
La rotación general entre dos sistemas de coordenadas rectangulares que tienen el mismo
origen puede escribirse en la forma:
 x'  x
   
 y '  = R1 (α)R2 ( β)R3 (γ ) y  (4.62)
 z'  z
   
donde α, β, γ son las rotaciones alrededor de los ejes x, y, z, respectivamente.
Las matrices ortogonales de rotación son:
1 0 0 
 
R1 (α) =  0 cos α sin α (4.63)
 
 0 − sin α cos α
86

96.  cos β 0 − sin β
 
R2 ( β) =  0 1 0  (4.64)
 
 sin β 0 cos β
 cos γ sin γ 0
 
R3 (γ ) =  − sin γ cos γ 0 (4.65)
 
 0 0 1
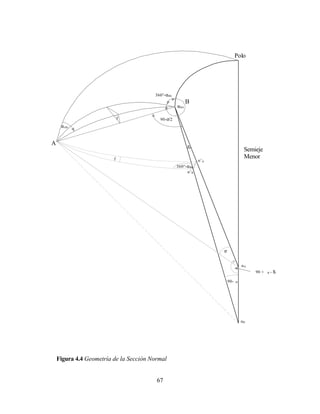
Esta conversión es para un sistema de coordenadas de mano derecha con rotaciones
positivas en el sentido de los punteros del reloj, como vistas desde el origen hacia la
proyección positiva de los ejes (Mueller, 1969).
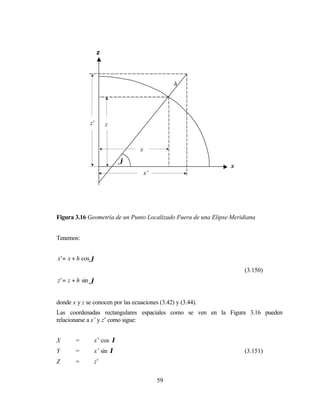
Utilizando la rotación general de (4.62) el sistema de coordenadas x, y, z se referirá a
∆X , ∆Y , ∆Z , y el sistema de coordenadas x’, y’, z’, se referirán a u, -v, w, puesto que –v
forma un sistema hacia la derecha. En nuestro caso, las rotaciones pueden lograrse con
una rotación de –(180º - λA) alrededor del eje z, y luego una rotación de –(90º - ϕA)
alrededor del nuevo eje y. Tenemos:
 u   ∆X 
   
 − v  = R2 [− (90 − ϕA )]R3 [− (180 − λA )] ∆Y  (4.66)
w  ∆Z 
   
Multiplicando estas matrices:
 u   − sin ϕA cos λA − sin ϕA sin λA cos ϕA   ∆X 
    
 v  =  − sin λA cos λA 0   ∆Y  (4.67)
    
 w  cos ϕA cos λA cos ϕA sin λA sin ϕA   ∆Z 
En términos de coordenadas individuales:
u = − sin ϕA cos λA ∆X − sin ϕA sin λA ∆Y + cos ϕA ∆Z (4.68)
v = − sin λA ∆X + cos λA ∆Y (4.69)
w = cos ϕA cos λA ∆X + cos ϕA sin λA ∆Y + sin ϕA ∆Z (4.70)
Si usamos (4.68) y (4.69) en (4.61) tenemos:
− sin λA ∆X + cos λA ∆Y
tan α = (4.71)
− sin ϕA cos λA ∆X − sin ϕA sin λA ∆Y + cos ϕA ∆Z
87

97. Si usamos (4.70) en lo último de (4.60) tenemos:
sin V =
1
(cos ϕA cos λA ∆X + cos ϕA sin λA ∆Y + sin ϕA ∆Z ) (4.72)
c
La distancia de la cuerda puede calcularse usando:
1 1
c = ( u 2 + v 2 + w2 ) 2 = ( ∆X 2 + ∆Y 2 + ∆Z 2 ) 2 (4.73)
De las ecuaciones en esta sección vemos un procedimiento para considerar la sección
normal y las cantidades relacionadas usando expresiones cerradas, en oposición a la gran
cantidad de expresiones en serie empleadas previamente. Las ecuaciones de esta sección
se usarán más adelante con el fin de desarrollar procedimientos para el cálculo de
posiciones geodésicas en el elipsoide. Sin embargo, nótese que en las ecuaciones
deducidas aquí los puntos pueden hallarse a cualquiera altura sobre el elipsoide.
4.2 La Curva Geodésica
Hasta ahora hemos considerado primordialmente la sección normal como una curva plana
en la superficie del elipsoide de referencia. Vimos que el uso de la sección normal tenía
la desventaja de no ser única en su género entre dos puntos. Ahora examinaremos una
curva, llamada geodésica, para la cual sólo hay una entre dos puntos cualquiera.
La definición fundamental de una curva geodésica es que ésta es una curva que da la
distancia más corta, en una superficie, entre de dos puntos cualquiera. Si la superficie es
un plano, la curva geodésica es una línea recta; si la superficie es una esfera, la geodésica
es un círculo máximo. En el elipsoide, la geodésica es una línea que tiene una curvatura
doble y, por tanto, no es una curva plana.
Para comenzar, consideremos la construcción de la geodésica sobre la superficie del
elipsoide. Primero nivelamos el teodolito con respecto al punto A y luego apuntamos
hacia un punto distante B, definiendo la curva de sección normal AaB. Después vamos a
B, se nivela el teodolito, se apunta hacia A para definir la sección normal BbA; luego
giramos el teodolito 180º y definimos un punto nuevo C, y la sección normal BbC.
Repetimos la operación yendo al punto C, punto D y puntos subsecuentes. Esta
construcción se muestra en la figura siguiente:
88

98. d
D
c
b C c
B b
A a
Figura 4.17 Secciones Normales Entre Puntos Cercanos
Sabemos que la separación de las líneas de la sección normal es pequeña y se reduce aún
más al disminuirse la separación entre puntos. Si dejamos que la distancia AB, BC, CD,
etc., se hagan más y más pequeñas, se obtendrá una curva singular entre los puntos. Esta
curva es la geodésica.
Si tuviera dos puntos A y B, podríamos construir la geodésica entre los dos puntos si
conociéramos el acimut apropiado de un segmento inicial. Dicha curva se ha construido
en la figura siguiente:
B
Sección Normal de B a A
B’
Geodésica entre A y B
A’
Sección Normal de A a B
A
Figura 4.17a La Geodésica entre Dos Secciones Normales
Un ejemplo de la relación de las curvas de la sección normal y la geodésica para dos
puntos ubicados en un elipsoide sumamente achatado, es mostrado en la Figura 4.18 de
Jordan (Volumen III, 2a mitad, Pág. 26).
89

99. Meridiano de B
Sección Normal en B
Meridiano de A B
Línea Geodésica
A Sección Normal en A
Figura 4.18 Una Geodésica y una Sección Normal en un Elipsoide Exageradamente
Achatado (f = 1/3)
De la definición de su construcción, claramente se observa una importante propiedad de
la geodésica. Dicha propiedad es aquella en que la normal principal de la geodésica en
cualquier punto, coincidirá con la normal del elipsoide en el punto. La normal principal
está contenida dentro del plano osculador que pasa a través de tres puntos infinitamente
cercanos en cada curva. Es evidente que una sección normal no tiene esta propiedad,
porque cada punto en la sección normal no contiene la normal en el punto.
Hasta este momento hemos considerado la geodésica en una interpretación geométrica.
Es posible encontrar ciertas propiedades de la geodésica mediante consideraciones
matemáticas que se presentan de la definición de la geodésica como una curva que tiene
la distancia más corta entre cualquiera de dos puntos.
Consideremos un triángulo diferencial en el elipsoide según se muestra en la Figura 4.19.
90

100. S
dα
Ncotϕ dλ
Mdϕ
α+dα
P1 P”
α P’
P
Figura 4.19 Una Figura Diferencial en el Elipsoide
Del triángulo recto diferencial, PP1 P’, escribimos:
ds cos α = Mdϕ
(4.74)
ds sin α = N cos ϕdλ
La ecuación (4.74) es válida para una curva arbitraria (por ejemplo, sección normal o
geodésica) en el elipsoide. Ahora especificamos que PP’P” yace sobre la geodésica. Esto
sería el caso si los tres puntos estuvieran en un plano vertical del elipsoide pasando a
través de P’, el cual es el plano osculador de la línea geodésica en P’ (Jordan, Vol. III, 2a
mitad, pág. 27). En este caso consideramos el triángulo PSP’ para encontrar que el ángulo
en S de este triángulo es dα. Por ello podemos escribir:
N cos ϕdλ
dα = N cot ϕ = sin ϕdλ (4.75)
Las ecuaciones (4.74) y (4.75) son las ecuaciones diferenciales primarias para la curva
geodésica en el elipsoide. También pueden escribirse dos ecuaciones más. Tenemos:
91

101. N cosϕ dλ
tanα = (4.76)
M dϕ
ds 2 = ( Mdϕ) 2 + ( N cos ϕdλ) 2 (4.77)
Si ahora dejamos p = N cos ϕ , y asumimos que en la geodésica la longitud está en
función de la latitud, es conveniente escribir la ecuación (4.77) como:
( ds ) 2 = M 2 + p 2 ( dλ ) 2 (4.78)
dϕ dϕ
o resolviendo para ds:
dϕ 2
ds = M 2 dϕ2 + p 2 dλ2 = M ( ) + p 2 dλ (4.79)
dλ
dϕ 2
Si dejamos que υ = M 2 ( ) + p 2 podemos escribir:
dλ
ds = υ⋅ dλ
Lo cual integramos para formar:
s = ∫υdλ (4.80)
Para que la curva definida por (4.80) sea una geodésica, el valor de la integral debe ser
mínimo. Esto resulta ser un problema de variación de cálculo que es resuelto en
Bagratuni (1967, pág. 83) y Jordan (Vol. III, 2a parte, pág. 30).
Después de trabajar la ecuación (4.80), sujeta a un criterio de distancia mínima, se
encuentra que la curva dada, o específicamente la geodésica, debe satisfacer la ecuación
siguiente:
p ⋅ sin α = constante (4.81)
Así, el producto del radio paralelo por el seno del acimut geodésico, en cada punto sobre
la geodésica, es una constante. Esta ecuación es conocida como la ecuación de Clairaut.
Una prueba alterna para (4.81) puede ser construida comenzando con el largo del radio
paralelo p:
p = N cos ϕ (4.82)
Diferenciando,
92

102. dp = − N ⋅ sin ϕ ⋅ dϕ + cos ϕ⋅ dN
Puesto que
c
N =V
Tenemos
dN = −c dV
dϕ V 2 dϕ
Pero
dV = −η2 t
dϕ V
Así
−N sin ϕ
dp = dϕ (4.83)
V2
Puesto que N = MV 2 , (4.83) se reduce a
dp = − M sin ϕdϕ (4.84)
Para la geodésica vimos que dα = sin ϕdλ , lo cual puede escribirse como:
M sin ϕdϕ
dα = Mdϕ dλ
Usando (4.84) tenemos:
−dp −dp
dα = dλ = cos ϕ dλ
Mdϕ ds
Usando la segunda ecuación de (4.74) podemos escribir:
dα = −sinα p
cos
α dp
que toma la forma:
p cos α ⋅ dα + sin α ⋅ dp = 0
93

103. lo que implica
p sin α = constante
que corresponde a la ecuación (4.81)
Si consideramos muchos puntos en una geodésica, se deduce de (4.81) que:
p1 sin α1 = p 2 sin α2 = p3 sin α3 = ... = una constante = k (4.85)
Para encontrar la constante involucrada en (4.85), podemos examinar la geodésica entre
dos puntos específicos. En el ecuador p = a, y dejamos que el acimut de la geodésica en
el ecuador sea αΕ . Entonces:
a sin αΕ = k (4.86)
Puesto que p es un máximo en el ecuador, el seno del acimut αΕ en el ecuador será lo
más pequeño.
El valor máximo del sin α se dará cuando α sea igual a 90º. Esto corresponderá al valor
más pequeño del radio paralelo pmin . De la ecuación (4.85) escribimos:
p min ⋅ sin 90 o = k
o (4.87)
p min = k
Claramente pmin ocurre en la latitud más alta (o máxima) alcanzada por la geodésica de
interés.
Si hubiéramos escrito en la ecuación (4.81) p = a cos β , tendríamos:
a cos β1 sin α1 = a cos β2 sin α2 = ... = k (4.88)
De esta ecuación tenemos:
cos β1 sin α1 = cos β2 sin α2 = ... = una constante = k
a (4.89)
Así, el producto de la latitud reducida y del acimut geodésico es una constante en cada
punto en la geodésica. En el ecuador β es igual a 0º, por tanto tenemos:
sin αΕ = k
a (4.90)
En la latitud máxima alcanzada (ϕH ó βH) por la geodésica α = 90º, tenemos de (4.89):
94

104. cos βH = k
a (4.91)
Igualando las ecuaciones (4.90) y (4.91) encontramos:
sin αΕ = cos βΗ (4.92)
Por tanto vemos que la máxima latitud reducida, alcanzada por una geodésica, es igual a
90º menos el acimut de la geodésica en el ecuador.
Concluimos la discusión concerniente al comportamiento general de una geodésica
mientras da vueltas alrededor del elipsoide. Tal geodésica es mostrada en la Figura 4.20
donde el acimut de la geodésica es αΕ .
Geodésica tangente
al paralelo Latitud máxima ϕH
A
B αE
Latitud mínima -ϕH Geodésica tangente
C al paralelo
Figura 4.20 La Geodésica en una Forma Continua
A medida que la geodésica va desde A a B y a C, su acimut continuamente cambiará.
Cuando el punto C es sobrepasado, la geodésica pasará más allá del ecuador en dirección
a hacerse tangente al paralelo ϕH . De específico interés es el hecho de que el cruce por el
ecuador, después de haber pasado por el punto C, no será exactamente de 180º en
longitud desde el punto de cruce B, sino en algún punto B’ generalmente al oeste de B.
Por ello, con pocas excepciones a discutirse en detalle más adelante, una geodésica no
repite su trayectoria. Hay en definitiva, un número infinito de distintos puntos de cruce
por el ecuador para una geodésica arbitraria. Una vista de tales cruces es mostrada en la
Figura 4.21, de Lewis (1963).
95

105. N A
P2
P1
P
Figura 4.21 Vista de una Geodésica Continua desde el Polo Norte Mostrando Cruces
Consecutivos en el Ecuador
4.2.1 Coordenadas Locales x, y, z en Términos de la Geodésica
Rescribiendo la ecuación del elipsoide (3.158) usando la siguiente anotación:
A = 1 + e '2 cos 2 ϕ = 1 + D
B = 1 + e' 2 sin 2 ϕ = 1 + D' (4.93)
1
C = − e' 2 sin 2ϕ
2
Para la ecuación del elipsoide tenemos (Tobey, 1928):
96

106. u = 0 = Ax 2 + y 2 + Bz 2 + 2Cxz − 2 Nz (4.94)
donde x = x ( s ); y = y( s ); z = z ( s ) , y por último s es la distancia geodésica.
Ahora consideramos una porción pequeña de la superficie del elipsoide conteniendo una
porción diferencial de la geodésica, según se muestra en la Figura 4.22 (Tobey, 1928):
D
P
C E
A B
N’ N
Figura 4.22 La Superficie Elipsoidal Conteniendo un Elemento Diferencial de Elipsoide.
Consideremos PACD y PBED porciones de la superficie u = 0. Dejemos que
PA = PB = ds sea una porción de la geodésica. PN, una línea perpendicular a AB, es la
normal principal.
En cualquier punto sobre la geodésica el plano osculador de la curva contiene la normal a
la superficie, de manera que la normal principal de la curva coincide con la normal a la
superficie. Este argumento puede expresarse escribiendo:
d 2x d 2 y d 2z
ds = ds = ds2
2 2
(4.95)
du du du
dx dy dz
Para aplicar esta ecuación asumimos una serie de potencias en s para x, y, z:
x = l 1 s + l 2 s 2 + l 3 s 3 + l 4 s 4 + ...
97

107. y = m1 s + m2 s 2 + m3 s 3 + m4 s 4 + ... (4.96)
z = n1 s + n 2 s 2 + n3 s 3 + n4 s 4 + ...
Ahora sustituimos (4.96) en (4.94) para obtener una ecuación a la enésima potencia en s.
Puesto que la ecuación entera es igual a cero, los coeficientes individuales de s deben ser
cero. Este resultado implicará que n1 = 0. Luego necesitamos implementar la condición
(4.95). Primero, calculamos las derivadas en el denominador de (4.95) usando (4.94):
du = 2( Ax + Cz)
dx
du = 2 y (4.97)
dy
du = 2( Bz + Cx − N )
dz
Las derivadas requeridas en el numerador son encontradas diferenciando (4.96)
d 2 x = 1 ⋅ 2l + 2 ⋅ 3l s + 3 ⋅ 4l s 2 + ...
2 3 4
ds 2
d 2y
= 1 ⋅ 2m2 + 2 ⋅ 3m3 s + 3 ⋅ 4 m4 s 2 + ... (4.98)
ds 2
d 2 z = 1 ⋅ 2 n + 2 ⋅ 3n s + 3 ⋅ 4n s 2 + ...
2 3 4
ds2
Luego sustituimos (4.97) y (4.98) en (4.95) e igualamos los coeficientes de las potencias
comunes de s. Después de algunas reducciones (Tobey, 1928, Proposición II) tenemos las
ecuaciones siguientes:
s Dl (1+l2 ) s 3 − C (1 + 8 l 2 ) s 4 + ...
x = lN sin N −
6N 2 24 N 3
s Dm l2 s 3 − Cm s 4 + ...
y = mN sin N − (4.99)
6N 2 3N 3
Cl(1+ D l2 ) 3 3D' − 6Dl 4
2
z = 2 N sin 2s + DlN +
2s 2
2
s + s
N 2 2N 2 24 N 3
donde
98

108. l =l 1 = cos α
m = m1 = sin α (4.100)
a
N=
1 − e sin 2 ϕ1
2
Conociendo un acimut geodésico (α) y la distancia s, podemos usar la ecuación (4.99)
para calcular las coordenadas de la geodésica basándose en un sistema local en el punto
inicial. Puesto que estas ecuaciones están en forma de serie, habrá una distancia más allá
en la cual las ecuaciones no serán lo suficientemente exactas. Ecuaciones similares
también pueden ser derivadas para una sección normal (Clarke, 1880, pág. 118).
4.2.2 Longitud de un Arco Diferencial de una Geodésica Rotada
Consideremos una geodésica desde el punto A con un largo s, y un acimut α. El punto
final de esta línea define un punto F. Ahora giramos la geodésica un ángulo dα de modo
que el punto final esté ahora en D. Dejamos que la distancia DF sea dge la cual ha de
determinarse. Usando el sistema de coordenadas locales x, y, z antes descrito, tenemos:
dg e2 = dx 2 + dy 2 + dz 2 (4.101)
Podemos diferenciar (4.99) tomando dα como la variable para encontrar dx, dy, dz.
Podemos simplificar (4.101) escribiendo:
dg e = wdα (4.102)
donde w es una cantidad a determinarse usando las derivadas de (4.99). Después de
alguna reducción (Apéndice 1, Tobey, 1928, Proposición IV) tenemos:
s R Cl s
w = R A sin R − A3 ( R ) 4 + ... (4.103)
A A
donde R A es el radio medio gaussiano en el punto A. w es l amado la longitud reducida
de la geodésica.
99

109. 4.2.3 Relación entre la Geodésica y la Longitud de la Cuerda
El largo de la cuerda c, entre dos puntos en el elipsoide, puede ser calculado desde:
c 2 = x 2 + y2 + z 2 (4.104)
Podemos expresar esto en términos de la longitud de la geodésica sustituyendo x, y, z de
(4.99). Para calcular c desde s, tenemos (Apéndice 1, Tobey, 1928, Proposición V):
c = 2 N sin 2s (1 − Dl ( N ) 2 − Cl ( N ) 3 + ...)
s s
2
(4.105)
N 12 8
donde N es el radio de curvatura del primer vertical en el primer punto. Esta serie puede
ser invertida para hallar s como una función de c:
1 2
s = c (1 + c 2 + Dl 2 c 2 + Cl3 c 3 + ...) (4.106)
24 N 2 12 N 8N
Clarke (1880, pág. 108) efectúa una derivación análoga a la anterior en donde se
relacionan la distancia de la sección normal s’, y la distancia de la cuerda. Sin derivación
tenemos:
s' = c(1 + c 2 (1 − 3F R ) + ( 3 + 3 H + 1 F 2 ) c 4 − ( 3 FH + 5 F 3 ) c 5 + ...)
c
2 4 5
24 Rα α 640 80 4 Rα 16 12 Rα
(4.107)
donde
fh f 2 − h2
F= ; H =
1+h2 1+h 2
e sin ϕ e cos ϕcosα
f = ; h=
1−e2 1−e2
y Rα es el radio de curvatura en el acimut de la sección normal.
4.2.4 Comparación de la Geodésica con la Sección Normal
Ahora trataremos la diferencia de distancia angular entre geodésicas y secciones
normales. Primero consideremos las diferencias acimutales comenzando con la Figura
100

110. 4.23 la que muestra las secciones normales y la geodésica entre dos puntos arbitrarios, A
y B.
P
B
α3
a
α2
α1
A
Figura 4.23 La Geodésica Localizada entre dos Secciones Normales
En esta figura:
α1 es el acimut de la sección normal, en A, desde A hasta B
α2 es el acimut de la geodésica, en A, desde A hasta B
α3 es el acimut de la sección normal, en A, desde B hasta A
La diferencia α1 − α3 fue calculada como ∆ y dada en la ecuación (4.32) ó (4.33). Para
determinar la diferencia α1 − α2 seguimos a Tobey (1928, Proposición VI) que
corresponde al Apéndice 1. Construimos en la figura 4.24 una sección normal AHFT en
el punto A con el acimut α1 . AH es tangente a esta sección normal. AF es la geodésica
desde A hasta F que tiene un acimut α2 . La sección normal en A, la cual pasa a través del
punto F (x, y, z) (sobre el elipsoide), también pasará a través del punto H(x, y, 0), donde H
está en la línea TF producida.
101

111. E
α1 H(xy0)
α2
s F(xyz)
S
A
T
K
Figura 4.24 Determinación de la Diferencia Acimutal entre una Sección Normal y una
Geodésica
La distancia AH es:
AH 2 = x 2 + y 2 (4.108)
que puede encontrarse usando (4.99)
AH = N sin s 1 − Dl ( s ) 2 − 3Cl ( s ) 3 + ...
2
  (4.109)
N 3 N 8 N 
Ahora el acimut de la sección normal puede ser determinado con:
cosα1 = x (4.110)
AH
Usando (4.99) y (4.109), Tobey demuestra que:
(αn − αg ) = (α1 − α2 ) =  Dlm ( s ) 2 + Cm ( s ) 3 + ... 
  (4.111)
 6 N 24 N 
102

112. Si sustituimos C, D, l , m tenemos
η2 s η2t s
(α1 − α2 ) = 6 ( ) 2 sin αcos α − 24 ( ) 3 sin α (4.112)
N N
donde:
η2 = e' 2 cos 2 ϕA
t = tan ϕA
α = acimut geodésico (ver 4.100)
Si consideramos solamente el primer término de (4.112), podremos comparar con (4.32)
esto nos dará la separación acimutal de las secciones normales contrarias. Concluimos
que:
(α1 − α2 ) ≈ 1 (α1 − α3 ) (4.113)
3
Este resultado nos indica que la geodésica triseca aproximadamente el ángulo entre las
secciones normales contrarias (o recíprocas), que yacen más cercanas a la sección normal
directa en el punto dado.
Como una estimación numérica de esta diferencia, considérese una línea de longitud s
ubicada en una latitud media de 45º y con un acimut de 45º. El valor de (α1 − α2 ) es por
tanto:
s ( km) (α1 − α2 )"
30 0, 001
60 0,005
100 0,014
120 0,020
Aunque la ecuación (4.113) implica que la geodésica siempre yace entre las dos
secciones normales, no siempre esto es verdad. Considere el caso de dos puntos en el
mismo paralelo donde sólo hay una sección normal. Entonces el valor de ∆ en (4.32) es
cero, de manera que (4.113) no es correcto. En este caso la geodésica estará hacia el lado
del polo de la sección normal yaciendo completamente fuera de ella. Para puntos no
exactamente en el mismo paralelo, la geodésica puede cruzar una curva de sección
normal.
103

113. En el caso de dos puntos en el mismo meridiano, hay solamente una sección normal. La
geodésica coincidirá con esta sección normal.
4.2.5 Diferencia de Longitud entre la Sección Normal y la Geodésica
Para derivar la diferencia de longitud sn – sg seguiremos a Tobey (1928, Proposición VII).
Consideramos dos puntos A y F que están conectados por la sección normal del acimut θ,
longitud sn y la geodésica del acimut α y longitud sg, según se muestra en la Figura 4.25.
D
dsg
dsn
C
F
sg
α sn
θ
A
Figura 4.25 Relación Diferencial entre Longitudes de Secciones Normales y Geodésicas
Rotamos la geodésica AF sobre la normal en A, un ángulo dα, y de este modo se genera
el arco dge = FC. De la ecuación (4.102) tenemos:
d ge = w dα (4.114)
Ahora extendemos la línea AC hasta D (en la sección normal AF) una cantidad dsg. El
cambio correspondiente de longitud, en la sección normal, es una distancia dsn . Luego
tenemos:
FD 2 = DC 2 + CF 2
ó
104

114. ds n = ds g + ( wdα) 2
2 2
(4.115)
Para encontrar dα diferenciamos (4.111) siendo las variables αg (ó α2 ) y ds. Tenemos:
  ds g
dα =  − Dlm  s  − Cm  s  + ... ⋅
2
 3 N      N (4.116)
 8 N 
Recordando el valor de w de (4.91) tenemos:
 
wdα =  − Dlm  s  − Cm  s  + ... ⋅ ds g
2 3
 3      (4.117)
 N 8 N 
Ahora sustituimos (4.117) en (4.115) para encontrar:
 ( Dlm) 2  s  4 
ds n = ds g 1 +
   + ... 
 (4.118)
 18  N  
Integramos esta expresión para encontrar:
 ( Dlm) 2  s  4 
sn = sg 1+
   + ... 
 (4.119)
 90  N  
Sustituyendo D, l, y m, y resolviendo para sn – sg tenemos:
e'4 cos 4 ϕ  s  4
sn − sg = s  
360  N  sin 2α
2
(4.120)
Esta diferencia de longitud de la línea es muy pequeña debido a la presencia de los
4
términos e ' y   . A una distancia de 1600 km, esta diferencia de longitud es tan
4 s
 
N
solo de 1 mm.
4.3 El Gran Arco Elíptico y la Curva de Alineación
Consideremos dos puntos, A y B, ubicados sobre la superficie del elipsoide. La
intersección del plano conteniendo A, B, y el centro del elipsoide, con la superficie del
elipsoide, es denominado la gran curva elíptica. Claramente sólo hay una gran curva
elíptica entre dos puntos. Para tal curva habrá un único acimut y distancia. En la práctica,
105

115. la gran curva elíptica es raramente usada, de modo que existe poca literatura sobre ella.
Bowring (1984) ha descrito cálculos de posición usando esta curva.
Otra curva que ha sido descrita entre dos puntos en la superficie es la curva de alineación
(Clarke, 1880, pág. 116; Baeschlin, 1948, sección 17). Para describirla, nuevamente
consideremos dos puntos A y B, en el elipsoide. Dejemos que AB sea la sección normal
desde A hasta B, y BA la sección normal desde B hasta A. Luego consideremos un
meridiano entre los meridianos de A y B. Las dos secciones normales interseptarán este
meridiano en Q1 y Q2 según se observa en la figura 4.26:
Z
Q2
B
L a
A Q1
Figura 4.26 La Curva de Alineación
Ahora definimos un punto L en el meridiano ZQ1 Q2 , de manera tal que el acimut de la
visual hacia A y B difiera exactamente 180º. Si esta operación es repetida para todos los
meridianos entre A y B, la conexión de todos los puntos L forman la curva de alineación.
Debido a su construcción esta curva estará más cerca a la geodésica entre los puntos A y
B. Como en la práctica la curva de alineación no se usa principalmente, no se brinda
información adicional sobre ésta.
4.4 Reducción Geométrica de Observaciones de Dirección o Acimut
106

116. Dejemos que D sea la dirección observada desde el punto A hacia el punto B. Para ciertas
aplicaciones de estos datos, en un ajuste de triangulación, es necesario aplicar dos
correcciones basadas en nuestra discusión previa. En la sección 4.24 consideramos la
diferencia acimutal entre la sección normal y la geodésica. Para convertir la dirección de
la sección normal a la correspondiente dirección geodésica, agregamos δ1 a la cantidad
observada, donde δ1 (ver ecuación (4.112)) es:
2
δ1 = 12  s  cos 2 ϕm sin 2αAB
e2  
N
Si el punto B observado está en una elevación h, debemos añadir la corrección para
conseguir la dirección correspondiente al punto B proyectado ahora en el elipsoide.
Dejamos que dicha corrección sea δ 2 , entonces su valor será (ver ecuación 4.46):
h
δ2 = 2M e 2 cos 2 ϕm sin 2αAB (4.121)
m
107

117. 5 SOLUCIÓN DE TRIÁNGULOS ESFÉRICOS Y ELIPSOIDALES
Una de las metas básicas de la geodesia es la determinación de las coordenadas
geodésicas de puntos georreferenciados a un elipsoide de referencia. En los
procedimientos de geodesia clásica esto es realizado usualmente mediante la
triangulación y/o trilateración donde medimos distancias y/o ángulos o direcciones para
definir triángulos en el elipsoide de referencia. Para efectuar cálculos de posición, en
ciertos casos es necesarios desarrollar procedimientos para resolver triángulos en el
elipsoide. Primero consideraremos el problema aproximando el elipsoide a una esfera y
buscaremos una solución para los triángulos esféricos. Tales triángulos son equivalentes a
triángulos elipsoidales hasta aproximadamente 200 km2 de área.
5.1 Exceso Esférico
Consideremos un triángulo en la esfera donde los tres ángulos esféricos son A, B, C. El
exceso esférico del triángulo es definido como la suma de los tres ángulos menos 180º.
Por tanto:
ε = Aº+ B º+C º − 180º (5.1)
Esta definición surge del hecho de que en un plano la suma de los ángulos en un triángulo
plano es exactamente 180º.
Si R es el radio de la esfera y F es el área del triángulo esférico, puede ser demostrado
rigurosamente que (Jordan, Vol. III, 1a mitad, pág. 89):
ε = F2 (5.2)
R
En consecuencia, el exceso esférico es proporcional al área de la figura.
Si los lados del triángulo son expresados en unidades de radianes tal como a, b y c, puede
lograrse una expresión alterna para el exceso esférico como (Jordan, Vol. III, 1a mitad,
pág. 17):
tan ε = tan s tan s −a tan s−b tan s−c (5.3)
4 2 2 2 2
108

118. donde a + b + c = 2s
ejemplos de magnitudes de excesos esféricos son entregados por Jordan (Vol. III, 1a
mitad, pág. 92), como sigue:
Área del Triángulo ε
1 km2 0,00507”
21 millas2 (triángulo equilátero, lados 11,25 km) 0,279”
200 km2 (triángulo equilátero, lados 21,5 km) 1”
Triángulo equilátero, lados 11,25 km 27”
5.2 Solución del Triángulo Esférico por el Teorema de Legendre
La solución de triángulos esféricos se simplifica si uno utiliza el teorema de Legendre el
cual dice lo siguiente: “Si los lados de un triángulo plano son iguales a los lados
correspondientes de un triángulo esférico, entonces los ángulos del triángulo plano serán
iguales a los ángulos correspondientes del triángulo esférico menos un tercio del exceso
esférico”. Este teorema fue derivado por Legendre en París en 1787. Para probar este
teorema consideremos un triángulo esférico (en una esfera de radio R) y el triángulo
plano correspondiente, según se muestra en la Figura 5.1.
C
C’
b a
b a
B
A A’ c B’
c
Figura 5.1 Triángulos Esférico y Plano
109

119. Usando estas figuras intentaremos encontrar la diferencia entre el ángulo en la esfera y el
ángulo en el plano, es decir ( A-A’), (B-B’), (C-C’). Para hacerlo primero aplicamos la ley
de cosenos al triángulo esférico, expresando:
cos a = cos R cos R + sin b sin R cos A
b c c (5.4)
R R
ó
cos a − cos b cos c
cos A = R R R (5.5)
sin b sin c
R R
Limitándonos a los triángulos pequeños, notamos que a/R, b/R, c/R serán pequeños, y que
una expansión en series de seno o coseno será apropiada. Omitiendo la quinta potencia de
a/R, b/R, y c/R, la ecuación (5.5) podría ser escrita como:
 1− a 2 + a 4  −1 − b 2 + b 4  1 − c 2 + c 4 
 2    
 2R 24R 4   2 R 2 24 R 4   2R2 24 R 4 
cos A = (5.6)
 b − b 3  c − c 3 
R  
 6 R 3  R 6 R 3 
Multiplicando los términos entre corchetes, y expandiendo el denominador, encontramos
(Jordan, Vol. III, 1a mitad, pág. 94):
b 2 + c 2 − a 2 a 4 + b 4 + c 4 − 2a 2 c 2 − 2b 2 c 2 − 2a 2 b 2
cos A = + + ... (5.7)
2bc 24 R 2 bc
Si aplicamos la ley de cosenos en el triángulo plano, tenemos:
a 2 = b 2 + c 2 − 2bc cos A' (5.8)
resolviendo para cos A se encuentra:
b2 + c 2 − a 2
cos A' = (5.9)
2bc
110

120. También podemos obtener una expresión para sen2 A’, desarrollando sen2 A’ = 1-cos2 A’,
de este modo, de la ecuación (5.9) tenemos
− a4 − b − c 4 + 2 a 2 b + 2a 2 c 2 + 2b 2 c 2
4 2
sin 2 A' = (5.10)
4b 2 c 2
Notamos que la ecuación (5.9) representa la primera parte de la ecuación (5.7), mientras
que la ecuación (5.10) está relacionada con la segunda parte de (5.7). Usando (5.10) y
(5.9) en la ecuación (5.7) encontramos:
bc sin 2 A'
cos A = cos A' − + ... (5.11)
6R 2
Ahora usamos (2.23) adoptando n = 1 de forma que:
x− y x+ y
cos x − cos y = − 2 sin 2 sin 2 (5.12)
Donde en nuestro caso x = A y y = A’. Con suficiente aproximación se toma:
x− y A− A' A− A'
2 = sin 2 ≈ 2
sin
(5.13)
x+ y
sin = sin A + A' ≈ sin A'
2 2
Puesto que la diferencia entre A y A’ será pequeña.
Combinando las ecuaciones (5.13), (5.12) con la ecuación (5.11), tenemos:
bc sin A'
A − A' = + ... (5.14)
6 R2
bc sin A'
El área del triángulo plano es , luego la ecuación (5.14) es escrita:
2
111

121. A − A' = P 2 + ... (5.15)
3R
De un modo similar puede demostrarse que:
B − B' = P2
3R
(5.16)
C −C' = P2
3R
Si sumamos la ecuación (5.15) y (5.16) y se observa que (A’ + B’ + C’) = 180º, tenemos:
A + B + C = 180º + P2 (5.17)
R
Comparando esto con la ecuación (5.1) ó (5.2) es claro que P/R2 es esencialmente el
exceso esférico del triángulo. Entonces las ecuaciones (5.15) y (5.16) pueden ser escritas
en la forma:
ε
A − A' =
3
B − B' = ε (5.18)
3
C − C' = ε
3
Estas ecuaciones son la justificación del teorema de Legendre.
Las ecuaciones (5.17) y (5.18) son solamente aproximaciones. Derivaciones más precisas
producen las siguientes ecuaciones ampliadas (Jordan, Vol. III, 1a mitad, pág. 110):
a 2 + 7b2 + 7c 2 
( A − A' ) = 3P 2 1 +
R   120 R2  + ...

7a 2 + b2 + 7c 2 
( B − B' ) = 3P 2 1 +  + ... (5.19)
R   120 R2 
112

122. 7 a2 + 7b 2 + c2 
(C − C' ) = 3P 2 1 +
R   120 R 2  + ...

Si sumamos estas ecuaciones tenemos:
a 2 + b 2 + c2 
A + B + C =180º + P2 1 + (5.20)
R  24R 2 

Por tanto al comparar con la ecuación (5.1) el exceso esférico del triángulo es:
a 2 + b2 + c2 
ε = R 2 1 +
P (5.21)

 24 R2 

En este momento notamos que el área P del triángulo plano puede ser encontrada
rigurosamente mediante:
P= s ( s − a)( s − b)( s − c) (5.22)
donde s = (a+b+c) /2.
Luego resolvemos P/R2 de la ecuación (5.21), y sustituimos los resultados en (5.19).
Tenemos (Jordan, Vol. III, 1a mitad, pág. 112):
( A − A' ) = ε + ε 2 ( m 2 − a 2 )
3 60 R
( B − B' ) = ε + ε 2 (m 2 − b 2 ) (5.23)
3 60 R
(C − C' ) = ε + ε 2 (m 2 − c 2 )
3 60 R
donde
a2 + b2 + c 2
m2 =
3
113

123. La ecuación (5.23) puede ser comparada con la ecuación (5.18) para ver que el teorema
de Legendre es solamente una aproximación.
Para aplicaciones en triángulos que son atípicos respecto de aquellos encontrados en la
triangulación ordinaria, es necesario derivar el teorema de Legendre para triángulos en el
elipsoide. En este caso ahora tratamos con el exceso elipsoidal. Una derivación completa
puede ser encontrada en Jordan (Vol. III, 2a mitad, pág. 66).
Para resumir la solución, primero designamos los vértices del triángulo elipsoidal como
A, B, C. En cada punto, la curvatura media es:
K a = ( MN ) − 1 ; K B = (MN ) −1 ; K C = ( MN ) C1
A B
−
(5.24)
La curvatura media es:
K A + KB + KC
Km = (5.25)
3
Entonces la relación entre los ángulos elipsoidales y los ángulos planos es:
ε K − Km
( A − A' ) = ε + 60 K m ( m 2 − a 2 ) + 12 A
ε
3 Km
ε ε K − Km
( B − B' ) = ε + 60 K m (m 2 − b 2 ) + 12 B (5.26)
3 Km
ε K − Km
(C − C' ) = ε + 60 K m ( m 2 − c 2 ) + 12 C
ε
3 Km
Los segundos términos en el lado derecho de (5.26) son los términos esféricos de
segundo orden (ecuación (5.23)), mientras que los terceros representan las contribuciones
elipsoidales. El valor de ε es:
114

124.  m2 K 
 m
ε = P Km  1 +
8 
(5.27)
 
 
El área del triángulo plano puede ser encontrada usando (5.22).
Como un ejemplo numérico se considera un triángulo descrito en Jordan (Vol. III, 2a
mitad, pág. 67) donde:
a = 69194 m
b = 105973 m
c = 84941 m
ϕA = 50º 51' 9"
ϕB = 51º 28' 31"
ϕC = 51º 48' 2"
El exceso elipsoidal de este triángulo es 14,850054”. L resultados de la evaluación de
os
(5.26) son los siguientes:
A − A' = 4,950018 + 0,000018 + 0,000148 = 4,950184"
B − B' = 4,950018 − 0,000021 − 0,000028 = 4,949969"
C − C ' = 4,950018 + 0,000003 − 0,000120 = 4,949901"
Notamos que las correcciones debido al uso de los triángulos elipsoidales son mayores
que las correcciones del término esférico de orden más alto.
5.3 Solución de Triángulos Esféricos por Aditamentos
En la solución de triángulos por el método de Legendre los lados de un triángulo se
mantuvieron fijos mientras que los ángulos fueron modificados. En el método por
aditamentos se mantienen fijos dos ángulos, mientras se cambia la longitud de los lados.
Para derivar este procedimiento se puede escribir la ley de senos en el triángulo esférico
mostrado en la Figura 5.2.
115

125. C
C
γ
γ’
b a
b’ a’
β
α α’ β’
B
A A c’ B
c
Figura 5.2 Triángulos para el Método de Aditamento
a
sin A sin R
sin B = sin b (5.28)
R
mientras que en el triángulo plano correspondiente (con ángulos inalterados)
sin A a '
= (5.29)
sin B b'
Igualando las ecuaciones (5.28) y (5.29) tenemos:
a a − a3 3
a − a 2
a' sin R R 6R3 = 6R
= = (5.30)
b' sin b b − b 3 3
R 3
b− b 2
R 6R 6R
Donde hemos retenidos los términos de la tercera potencia en (a/R o b/R). Podemos
satisfacer esta ecuación si establecemos:
116

126. a' = a − a 2
3
6R
(5.31)
b' = b − b 2
3
6R
o para un lado arbitrario.
s' = s − s 2
3
(5.32)
6R
El valor de s3 /6R2 se llama el aditamento lineal para el lado s. Para distintos valores s,
esta corrección es aproximadamente como sigue: (ϕm = 50º) :
s ( km) s3 ( m)
6 R2
10 0,004
20 0,033
30 0,111
40 0,262
50 0,512
60 0,884
80 2,096
100 4,093
El uso de aditamentos fue primeramente en una forma logarítmica, como es mostrado en
Jordan (Vol. III, 1a mitad, pág. 98). Considerando que hoy en día este procedimiento no
es usado mayormente, no lo examinaremos con más detalles por ahora.
117

127. 6 CÁLCULO DE LAS COORDENADAS GEODÉSICAS
(SOLUCIONES DEL TRIÁNGULO POLAR ELIPSOIDAL)
6.1 Introducción
Ahora nos abocaremos al cálculo de las coordenadas geodésicas de los puntos en el
elipsoide. Tales coordenadas son usualmente especificadas como latitud y longitud.
Supongamos tener las coordenadas de un punto de inicio, la distancia y el acimut hacia
un segundo punto, y deseamos calcular las coordenadas del segundo punto, así como
también el acimut desde el segundo punto al primero. Tal problema es definido como el
problema geodésico directo o simplemente el problema directo.
El problema geodésico inverso es definido como el caso donde las coordenadas de los
puntos finales de la línea se conocen, y deseamos encontrar el acimut desde el punto uno
al punto dos, el acimut del punto dos al punto uno, y la distancia entre los dos puntos.
La solución de cualquiera de estos problemas es básicamente una solución del triángulo
polar elipsoidal, mostrado en la Figura 6.1.
Polo
∆λ
∆λ=λ2 -λ1
α21
α12 P2 (ϕ2 ,λ2 )
P1 (ϕ1 ,λ1 )
Figura 6.1 El Triángulo Polar Elipsoidal
Podemos expresar los problemas definidos previamente en la forma funcional siguiente:
118

128. Problema Directo:
ϕ2 = f1 (ϕ1 , λ1 ,α12 , s)
λ2 = f 2 (ϕ1 , λ1 , α12 , s) (6.1)
α21 = f 3 (ϕ1 , λ1 , α12 , s)
Problema Inverso:
s = f 4 (ϕ1 , λ1 , ϕ2 , λ2 )
α12 = f 5 (ϕ1 , λ1 , ϕ2 , λ2 ) (6.2)
α21 = f 6 (ϕ1 , λ1 , ϕ2 , λ2 )
Hay varias soluciones para estos problemas. Tales soluciones generalmente se
clasificaron por las distancias para las cuales ellas son válidas y por el tipo (por ejemplo
sección normal o geodésica) de línea que se está considerando. Podríamos tener técnicas
de solución simple para distancias cortas, mientras que para líneas largas se necesitan
fórmulas más extensas. Estudiaremos las ecuaciones para líneas cortas y medianas en las
siguientes secciones.
6.2 Desarrollo de Series en Potencias de s (Legendre)
6.2.1 El Problema Directo
Supongamos que una curva en el elipsoide puede ser expresada como una función de s:
ϕ = ϕ (s)
λ = λ (s) (6.3)
α = α (s)
119

129. Ahora desarrollamos la ecuación (6.3) dentro de una serie de MacLaurin referiendo el
primer punto como un origen:
dϕ d 2ϕ s 2
ϕ = ϕ1 + s+ + ...
ds 1 ds 2 1 2
λ = λ1 + dλ s + d λ s + ...
2 2
(6.4)
ds 1 2
ds 1 2
α21 = α21 + 180 º + ∆α = α12 + 180º +  dα  s +  d α  s + ...
2 2
   2  2
 ds  1  ds  1
α12 es el acimut directo en el punto 1, mientras que α21 es el acimut inverso en el punto
2. Ahora comenzamos la evaluación de las derivadas recordando las ecuaciones (4.74) y
(4.75):
ds cos α = Mdϕ
ds sin α = N cos ϕdλ (6.5)
dA = sin ϕdλ
Recordamos que
M = c3 ; N = V
c
V
Por tanto, después de sustituir M y N, tenemos de (6.5):
dϕ 1 3
= V cos α = cosα (6.7)
ds c M
dλ = V sin α = sin α (6.8)
ds c cos ϕ N cos ϕ
Si despejamos d λ en la ecuación (6.8) y sustituimos dentro de dα = sin ϕ ⋅ dλ , tenemos:
120

130. dα = V sin αtan ϕ (6.9)
ds c
Para efectuar la diferenciación requerida en la ecuación (6.4) necesitaremos la derivada
de V con respecto aϕ , puesto que:
dV = dV dϕ
ds dϕ ds
Tenemos:
V = 1 + e' 2 cos 2 ϕ
dV = −e'2 sin ϕcosϕ
dϕ V
Dejando:η2 = e' 2 cos 2 ϕ , y t = tan ϕ tenemos:
V 2 = 1 + η2
dV = −η2t (6.10)
dϕ V
dV = − η2 V 2 cos αt
ds c
Para encontrar las segundas derivadas requeridas en la ecuación (6.4) primero escribimos:
d 2ϕ d  V 3  3V 2 dV V3
= ds  cos α = cos α − sin α dα
ds2 c ds ds
 c  c
Usando las ecuaciones (6.9) y (6.10) encontramos:
121

131. d 2ϕ −V 4
= 2 (sin 2 α t + 3 cos 2 αη2 t ) (6.11)
ds 2 c
Una forma compacta de esas derivadas puede ser obtenida dejando:
s sin α V s sin α
V = N = c
(6.12)
s cos α V s cos α
u= =
N c
Entonces las derivadas de ϕ con respecto a s son las siguientes (Jordan, Vol. III, 2a
mitad, pág. 77):
dϕ s
= +u
ds V 2
d 2ϕ s 2
2
ds V 2
(
= −v 2 t − u 2 3η2 t )
d 3ϕ s 3
3 2
( ) (
= −v 2 u 1 + 3t 2 + η2 − 9η2 t 2 − 3u 3η2 1 − t 2 + η2 − 5η2 t 2 )
ds V
d 4ϕ s 4
4
ds V 2
( ) ( )
= + v 4 t 1 + 3t 2 + η2 − 9η2 t 2 − 2v 2 u 2 t 4 + 6t 2 − 13η2 − 9η2 t 2 − 17η4 + 45η4 t 2 +
(
+ u 4 t η2 12 + 69η2 − 45η2 t 2 + 57η4 − 105η4 t 2 )
d 5ϕ s 5
5 2
( ) (
= +v 4 u 1 + 30t 2 + 45t 4 − 2v 2 u 3 4 + 30t 2 + 30t 4 )
ds V
(6.13)
En estas expresiones todos los términos son mantenidos hasta la derivada de cuarto
orden, pero todos los términos de ηn en la quinta derivada se han llevado a cero.
Seguidamente, consideramos d λ diferenciando la ecuación (6.8):
2
ds 2
122

132. ds 2 ds ds
[ ]
d 2 λ = d dλ = 1 sin α dV + V cosα dα + V tan ϕ sin α dϕ
c cosϕ ds c cosϕ ds c cos ϕ ds
(6.14)
dϕ
Sustituyendo el valor de dV de (6.10), dα de (6.9) y de (6.7), tenemos:
ds ds ds
d 2 λ = 2V 2 sin α cos αt = V 2t sin 2α (6.15)
ds 2 c 2 cos ϕ c2 cos ϕ
Usando la notación de (6.12), las derivadas (hasta el orden quinto) son:
dλ
s cos ϕ = + v
ds
d 2λ 2
s cos ϕ = +2vut
ds 2
d 3λ 3
3
( )
s cos ϕ = +2vu2 1 + 3t 2 + η2 − 2v 3 t 2 (6.16)
ds
d 4λ 4
ds 4
( )
s cos ϕ = 8vu 3 t 2 + 3t 2 + η2 − η4 − 8v 3 ut 1 + 3t 2 + η2( )
d 5λ 5
( ) ( ) (
s cos ϕ = 8vu 4 2 + 15t 2 + 15t 4 − 8v 3 u 2 1 + 20t 2 + 30t 4 + 8v 5 t 2 1 + 3t 2 )
ds 5
Seguidamente diferenciamos la ecuación (6.9):
ds 2 ds ds
[ ]
d 2α = d dα = sin α t dV + V (1 + t 2 ) sin α dϕ + V cos α ⋅ t ⋅ dα
c ds c ds c ds
La sustitución apropiada de las derivadas da:
ds 2 c2
(
d 2α = V 2 sin α cos α 1 + 2t 2 + η2 ) (6.17)
123

133. Los valores de estas derivadas hasta el quinto orden son:
dα
s = vt
ds
d 2α 2
2
(
s = vu 1 + 2t 2 + η2 )
ds
d 3α 3
3
( ) (
s = vu 2 t 5 + 6t 2 + η2 − 4η4 − v 3 t 1 + 2t 2 + η2 )
ds
d 4α 4
4
(
s = vu 3 5 + 28t 2 + 24t 4 + 6η2 + 8η2 t 2 − 3η4 + 4η4 t 2 − 4η6 + 24η6 t 2 − )
ds
(
− v 3 u 1 + 20t 2 + 24t 4 + 2η2 + 8η2 t 2 + η4 − 12η4 t 2 )
d 5α 5
5
( ) ( ) (
s = vu 4 t 61 + 180t 2 + 120t 4 − v 3 u 2 t 58 + 280t 2 + 240t 4 + v 5 t 1 + 20t 2 + 24t 4 )
ds
(6.18)
Si ahora sustituimos estas derivadas dentro de la forma general representada por (6.4),
obtenemos las siguientes ecuaciones de trabajo (Jordan, Vol. III, 2a mitad, pág. 78).
ϕ2 −ϕ1 1 2 3 2 2 v2 u u3 2
V2 = u − 2 v t − 2 u η t − 6 (1 + 3t + η − 9η t ) − 2 η (1 − t ) +
2 2 2 2 2
+ 24 t (1 + 3t 2 + η2 − 9η2 t 2 ) − v12 t ( 4 + 6t 2 − 13η2 − 9η2 t 2 ) + u n 2 t +
v4 2u 2 4
2
+ v u (1 + 30t 2 + 45t 4 ) − v u (2 + 15t 2 + 15t 4 )
4 2 3
120 30
(ë 2 − ë 1 ) cosϕ = v + vut − v33 t 2 + vu2 (1 + 3t 2 + η2 ) − v3u t(1 + 3t 2 + η2 ) + vu3 t( 2 + 3t 2 + η2 ) +
3
3
3
v5 4 3 2
+ 16 t 2 (1 + 3t 2 ) + vu ( 2 + 15t 2 + 15t 4 ) − v15 (1 + 20t 2 + 30t 4 )
u
15
(6.19)
124

134. á 21 − (á 12 ± 180º ) = vt + vu (1 + 2 t 2 + η 2 ) − v t (1 + 2t 2 + η 2 ) +
3
u 6
+ vu t ( 5 + 6 t 2 + η 2 − 4η 4 ) − v u (1 + 20 t 2 + 24 t 4 + 2η 2 + 8η 2 t 2 ) +
2 3
6 24
+ vu ( 5 + 28 t 2 + 24 t 4 + 6η 2 + 8η 2 t 2 ) + 120 t (1 + 20 t 2 + 24 t 4 ) −
v5
3
24
− v u t (58 + 280 t 2 + 240 t 4 ) + 120 t ( 61 + 180 t 2 + 120 t 4 )
vu 4
3 2
120
Todas las unidades angulares en estas expresiones estarán en radianes. Recuérdese
también que estas ecuaciones sirven específicamente para la línea geodésica. La precisión
de las ecuaciones ampliada es tal que Bagratuni (1967, pág. 136) indica que estas
fórmulas pueden ser usadas hasta 130 km. No obstante, Grushinsky (1969, pág. 62)
indica que dichas fórmulas son útiles hasta los 600-800 km. Desarrollos más precisos
serán presentados más adelante.
6.2.2 La Solución Inversa
La solución del problema inverso usando desarrollos en serie no es tan directa como lo
expresa la ecuación (6.4). Resolveremos este problema usando los primeros términos de
la ecuación (6.19) usando un procedimiento iterativo. Escribimos (6.19) en la forma.
3
V
ϕ2 − ϕ1 = 1 cos α12 ⋅ s + ∆ A
c
(6.20)
V1 sin α12
λ2 − λ1 = ⋅ s + ∆B
c cos ϕ1
donde ∆ A y ∆ B son funciones de s,α12 , y ϕ1 . Ahora resolvemos la ecuación (6.20)
asumiendo que ∆ A y ∆ B son conocidas. Consideremos que ∆ϕ = ϕ2 − ϕ1 y que
∆λ = λ2 − λ1 , entonces tenemos:
125

135. V1 sin α12
⋅ s = ∆λ − ∆ B
c cosϕ1
(6.21)
V13
cos α12 ⋅ s = ∆ϕ − ∆ A
c
Dividiendo estas dos ecuaciones y reordenando los términos queda:
∆λ − ∆
tan α12 = V1 2 cos ϕ1  ∆ϕ − ∆B 
  (6.22)
 A
Adicionalmente, s puede ser encontrado desde cualquiera de las ecuaciones dadas en
(6.21). Por ejemplo, para la segunda expresión:
c( ∆ϕ − ∆ A )
s= (6.23)
V13 cos α12
Sabiendo que ∆λ, ∆ϕ , yϕ1 , y dejando ∆ A y ∆ B en cero como una primera aproximación
( )
al acimut α12) tenemos de la ecuación (6.22):
(1
tan α12 ) = V12 cos ϕ1  ∆ϕ 
(1 λ (6.24)
∆ 
 
Dejando otra vez ∆ A igual a cero, ahora en la ecuación (6.23), y usando el acimut de
(6.24) calculamos la primera aproximación de la distancia como:
( 1) c ∆ϕ
s = (6.25)
V cosα(1 )
1
3
12
Usando ahora los valores conocidos de α12) y s (1 ) , podemos calcular valores para ∆ A y
(1
∆ B los que pueden ser usados en las ecuaciones (6.22) y (6.23) para conseguir mejores
valores de α12 y s. El proceso es iterado hasta que los valores de α12 y s no cambien más
allá de una cantidad especificada.
126

136. 6.3 Las Fórmulas de Puissant
Estas ecuaciones fueron originalmente deducidas por Puissant en el siglo XVIII. Ellas
han sido extendidas y usadas por varias organizaciones geodésicas para sus trabajos de
cálculo de posición. Estas ecuaciones no son derivadas con gran rigor y normalmente no
son usadas para líneas mayores de 100 km de longitud.
6.3.1 El Problema Directo
Para derivar las ecuaciones necesarias del problema directo, consideremos una esfera de
radio N1 , tangente a lo largo del paralelo a través del primer punto. Para distancias cortas,
la esfera será aproximadamente coincidente con el segundo punto. Supongamos que el
acimut y la distancia sean iguales en la esfera y en el elipsoide. Esta información se
muestra en la Figura 6.2:
P’
90°- ϕ ’
1
P
90°- ϕ ’
2
s
α12
P2 (ϕ ,λ )
2 2
P1 (ϕ ,λ )
1 1
Figura 6.2 Aproximación de Puissant para Determinar la Latitud
90 − ϕ1' y 90 − ϕ2 son arcos en una esfera de radio N1 , tangente al punto uno. En la
'
medición de estos arcos tenemos ϕ1' = ϕ1 , esto porque la esfera es tangente en el primer
punto. Considerando el triángulo esférico P1 P’P2 , escribimos la ley de cosenos:
127

137. sin ϕ2 = sin ϕ1 cos ( P1 P2 ) + cos ϕ1 sin ( P1 P2 ) cos α12
'
(6.26)
Debido a que estamos tratando con distancias cortas, dejamos que ϕ2 = ϕ1 + ∆ϕ' donde
'
∆ϕ' es una cantidad pequeña en radianes. Además dejemos que el arco P1 P2 sea
considerado como s/N1 . La ecuación (6.26) ahora se convierte en:
s s
sin (ϕ1 + ∆ϕ' ) = sin ϕ1 cos N + cos ϕ1 sin N cos α12 (6.27)
1 1
Ahora desarrollamos en serie sin (ϕ1 + ∆ϕ') :
∆ϕ' 2 ∆ϕ'3
sin (ϕ1 + ∆ϕ' ) = sin ϕ1 + cos ϕ1 ∆ϕ' − sin ϕ1 − cos ϕ1 + (6.28)
2 6
Considerando que s/N 1 es pequeño, escribimos:
sin N = N − s 3
s s 3
1 1 6 N1
(6.29)
2
cos s = 1 − s 2
N1 2 N1
Podemos sustituir la ecuación (6.28) y (6.29) dentro de (6.27) y resolver ∆ϕ' .
Encontramos:
∆ϕ'2 ∆ϕ'3
∆ϕ' = N cos α12 − s 2 tan ϕ1 − s 3 cos α12 +
s 2 3
tan ϕ1 + (6.30)
1 2 N1 6 N1 2 6
Puesto que ∆ϕ' aparece en el lado derecho de la ecuación (6.30) debemos resolver la
ecuación por aproximaciones sucesivas. En la primera aproximación tomamos
∆ϕ' = s cosα12 / N1 así (6.30) se transforma en:
∆ϕ'3
∆ϕ' = N cos α12 − s 2 tan ϕ1 sin 2 α12 − s 3 cos α12 + 6
s 2 3
(6.31)
1 2 N1 6 N1
128

138. Por tanto, una mejor aproximación para ∆ϕ' es:
∆ϕ' = N cos α12 − s 2 tan ϕ1 sin 2 α12
s 2
(6.32)
1 2 N1
La ecuación (6.32) ahora podría ser sustituida nuevamente dentro de la ecuación (6.30)
para encontrar:
∆ϕ' = N cos α12 − s 2 sin 2 α12 tan ϕ1 − s 3 cos α12 sin 2 α12 (1 + 3 tan 2 ϕ1 ) (6.33)
s 2 3
1 2 N1 6 N1
Ahora debemos cambiar ∆ϕ' (medido en la esfera de radio N1 ) a ∆ϕ el cual es medido a
lo largo de un arco de meridiano. Para hacerlo, asumimos que la distancia N1 ∆ϕ' en la
esfera es igual a la distancia correspondiente en el elipsoide. Permitiendo que Mm sea el
radio de curvatura del meridiano en la latitud media, tenemos:
N1 ∆ϕ' = M m ∆ϕ (6.34)
el cual puede resolverse para encontrar ∆ϕ si encontramos Mm. Para evaluar Mm
necesitamos conocer la latitud del segundo punto, lo cual es lo que tratamos de hacer.
Para resolver el problema, hallamos Mm mediante un desarrollo en serie de M alrededor
del primer punto. Por tanto:
∆ϕ
M m = M 1 + dM + ... (6.35)
dϕ 1 2
o después de la diferenciación:
M e 2 sin ϕ1 cosϕ1
Mm = M1 + 3 1
2 (1 − e 2 sin 2 ϕ1 ) ∆ϕ (6.36)
Resolviendo ∆ϕ de (6.34) y sustituyendo (6.36) dentro de esta expresión, tenemos:
129

139. ∆ϕ = δϕ − cδϕ∆ϕ (6.37)
donde
δϕ = M cos α12 − 2 N M sin 2 α12 tan ϕ1 − s2 sin 2 α12 cos α12 (1 + 3 tan 2 ϕ1 )
s s2 3
1 1 1 6 N1 M 1
(6.38)
y
e2 sin ϕ1 cos ϕ1
c =3 (6.39)
2 (1−e2 sin 2 ϕ1 )
Puesto que (δϕ − ∆ϕ) es pequeño, podemos permitir que δϕ∆ϕ de la ecuación (6.37)
sea: (δϕ) 2 . Con esta sustitución e introduciendo los símbolos siguientes (Hosmer, 1930,
pág. 212):
1 tan ϕ1 3e 2 sin ϕ1 cosϕ1
B= M , C = 2M N , D= ,
1 1 1 2(1−e 2 sin 2 ϕ1 )
(6.39a)
1 + 3 tan 2 ϕ1 s cos α12
E= , h=
6 N12 M1
tenemos:
∆ϕ = s cos α12 B − s 2 sin 2 α12 C − hs 2 sin 2 α12 E − (δϕ) 2 D (6.40)
donde δϕ está dado por la ecuación (6.38) o por la suma de los primeros tres términos en
la ecuación (6.40). La latitud del segundo punto será entonces ϕ2 = ϕ1 + ∆ϕ .
Para determinar la longitud del segundo punto definimos una esfera de radio N2 , tangente
al paralelo a través de P2 . Asumimos que esta esfera pasa cerca del primer punto, de
manera que el acimut y distancia en el elipsoide y en la esfera sean los mismos. Esta
situación es mostrada en la Figura 6.3.
130

140. P’’
∆λ
90°- ϕ2
P
∆λ
s
α12
P2 (ϕ ,λ )
2 2
P1 (ϕ ,λ )
1 1
Figura 6.3 Aproximación de Puissant para Determinar la Longitud
Aplicando la ley de senos al triángulo esférico P1 P2 P”, tenemos:
sin ∆λ sin α12
=
 s  cos ϕ2
sin  
 N2 
de este modo:
s
sin ∆λ = sin ( N ) sin α12 sec ϕ2 (6.41)
2
La ecuación (6.41) es una expresión cerrada para un resultado aproximado. La longitud
del segundo punto podría ser λ2 = λ1 + ∆λ . La ecuación (6.41) podría también ser
desarrollada dentro de las series siguientes (Clark, 1957, Vol. II, pág. 336).
s 1 − s 2 (1 − sin 2 α sec 2 ϕ )
∆λ = N sin α12 sec ϕ2  6 N2 2  (6.42)
 
2 12
2
131

141. Deberíamos notar que antes de aplicar las ecuaciones (6.41) ó (6.42), es necesario
calcular la latitud del segundo punto usando la ecuación (6.40). Para calcular el acimut
inverso aplicamos la ecuación siguiente, obtenida de las analogías de Napier:
cos 1 (b−c )
tan ( B + C) = cot A
1 2
(6.43)
2
cos 1 (b+c ) 2
2
donde por analogía con la Figura 6.1, tenemos:
B = α12 b = 90º − ϕ2 '
C = 360º − α12 c = 90 º − ϕ1 (6.44)
A = ∆λ
que puede ponerse dentro de la ecuación (6.43) para encontrar:
cos 1 (90 − ϕ2 ) − ( 90 − ϕ1 ) 
2 
'
 

tan 1 (α12 + 360º−α21 ) = cot ∆λ (6.45)
1  ' ) + (90 − ϕ ) 
2
2
cos 2 (90 − ϕ2 1 
 
Escribimos α21 = α12 + ∆α ± 180º para que la ecuación (6.45) llegue a ser, (después de
invertirse):
α sin 2 (ϕ1 +ϕ2 ) tan ∆λ
1 '
tan ∆2 = (6.46)
cos ∆ϕ' 2
2
Puesto ϕ'2 ≅ ϕ2 y ∆ϕ' ≅ ∆ϕ la ecuación (6.46) puede escribirse como:
α sin ϕm tan ∆λ
tan ∆2 = (6.47)
cos ∆ϕ
2
2
132

142. La ecuación (6.47) puede escribirse en forma de series como sigue (Clark, 1957, Vol. II,
pág. 337):
∆ϕ ∆ϕ ∆ϕ
∆α = ∆λ sin ϕm sec 2 + ∆λ (sin ϕm sec 2 − sin 3 ϕm sec 3 2 )
3
(6.48)
12
Las ecuaciones (6.40), (6.41), y (6.42) (o formas de series equivalentes para las dos
últimas), constituyen una implementación usual de las ecuaciones de Puissant. Ellas han
sido usadas para distancias en el orden de 100 km. Un término adicional que ha de
añadirse al lado derecho de (6.40) extiende la precisión del procedimiento para líneas de
mayor extensión. Este término es (Hosmer, 1930, pág. 219):
1 s 2 kE − 3 s 2 cos 2 αkE − 1 s 2 cos 2 αsec 2 ϕAk (6.49)
2 2 2
donde
k = s 2 sin 2 αC
1 (6.50)
A=
N1
Si se calculan líneas cortas (de hasta aproximadamente 12 millas o 19 km), pueden darse
versiones simplificadas de las ecuaciones de Puissant. De la ecuación (6.40) podríamos
escribir:
∆ϕ = s cos α12 ⋅ B − s 2 sin 2 α12 ⋅ C − (δϕ) 2 D (6.51)
De la ecuación (6.42) podríamos escribir:
s
∆λ = N sin α12 sec ϕ2 (6.52)
2
y de la ecuación (6.48) tenemos:
∆α= ∆λ sin ϕm (6.53)
133

143. 6.3.2 El Problema Inverso
Para resolver el problema inverso usando las ecuaciones de Puissant, primero resolvemos
la ecuación (6.24) de la forma siguiente:
N2 ∆λcos ϕ2
s sin α12 =  
(6.54)
1− s 2 2 (1−sin 2 α12 sec 2 ϕ2 )

 


6N 2 

Si como una primera aproximación se deja el denominador en uno, podemos
calcular s sin α12 . Luego resolvemos s cosα12 de la ecuación (6.40):
1 [
s cos α12 = B ∆ϕ + s 2 sin 2 α12 ⋅ C + hEs 2 sin 2 α12 + (δϕ) 2 D ] (6.55)
Aunque desconocemos h en el lado derecho de la ecuación, podemos encontrar una buena
aproximación para s cosα12 . Entonces
s sin α12
tan α12 = s cos α ; s =
12
(s sin α12 )2 + (s cos α12 )2 (6.56)
Donde podemos encontrar α12 y s. Será necesario la iteración para alcanzar una precisión
compatible con la del problema directo.
Deberíamos notar que la derivación de las ecuaciones de Puissant es tal que no podemos
indicar si el método es para una geodésica o para una sección normal. Esto no es
relevante considerando que la aplicación de dichas ecuaciones se limitan a extensiones de
líneas donde la diferencia entre curvas geodésica y curvas de sección normal no es
significante.
134

144. 6.4 Las Fórmulas de la Latitud Media de Gauss
Las ecuaciones de Puissant son convenientes para la solución del problema directo, pero
son menos convenientes para resolver el problema inverso. Para evitar esa dificultad es
apropiado considerar las fórmulas de la latitud media de Gauss (Lambert y Swick, 1935;
Lauf, 1983). En este procedimiento reemplazamos el triángulo polar elipsoidal por un
triángulo esférico que tiene por radio el radio de curvatura del primer vertical de la latitud
media entre los dos puntos. El triángulo elipsoidal P1 P2 P, y el triángulo esférico
correspondiente P1 ’P2 ’P’ se muestran en las siguientes figuras:
P P
∆λ ∆λ
90°- ϕ ’ 90°- ϕ ’
2
1
α21
s α12
α α21
P2 ’
12
P2 P1 ’
P1
Figura 6.4 Triángulos Polares Resueltos Mediante las Fórmulas de la Latitud Media de
Gauss
Asumimos que los acimuts y distancias en los triángulos elipsoidales y triángulos
esféricos son iguales. Sin embargo, notamos que ϕ1’ y ϕ2’ no son iguales a ϕ1 y ϕ2
porque las cantidades son medidas respecto de superficies diferentes. Asumiremos que:
ϕ m = 1 (ϕ1 + ϕ2 ) = 1 (ϕ1' + ϕ2 )
'
(6.57)
2 2
También asumiremos que la distancia del arco entre los paralelos de ϕ1’ y ϕ2’ sobre la
esfera es igual a la distancia entre los paralelos de ϕ1 y ϕ2 en el elipsoide. Sabiendo que el
radio de la esfera es Nm y, con suficiente precisión que el radio de curvatura del
meridiano en el elipsoide es Mm, podemos escribir:
N m (ϕ2 − ϕ1' ) = M m (ϕ2 − ϕ1 ) = M m ∆ϕ
'
(6.58)
135

145. Esta ecuación es similar a la (6.34) utilizada en la derivación de las ecuaciones de
Puissant. Ahora utilizamos las siguientes ecuaciones de Gauss o Delambre escritas para
el triángulo esférico siguiente:
C
a
b
B
c
A
Tenemos:
sin c cos 1 ( A − B) = sin 1 ( a + b) sin C
2 2 2 2
(6.59)
c C
sin sin 1 ( A − B) = sin 1 ( a − b) cos
2 2 2 2
En nuestro caso:
c= Ns C = ∆λ
m
A = α12
'
a = 90º − ϕ2
'
B = 360º − α12
'
b = 90º − ϕ1'
Así:
136

146. A − B = α12 + α21 − 360º a + b = 180 º − (ϕ1' + ϕ2 )
'
α21 = α12 + ∆α+ 180º a − b = ϕ1' − ϕ2
'
(6.60)
A − B = 2α12 + ∆α − 180º
Sustituyendo estos valores en la ecuación (6.59) tenemos, después de varias
simplificaciones:
sin 2 N sin (α12 + ∆α) = cos ϕm sin ∆λ
s (6.61)
m
2 2
∆ϕ'
sin 2 N cos (α + ∆α) = sin
s cos ∆λ (6.62)
m 12 2 2 2
De la ecuación (6.58) despejamos ∆ϕ' en términos de ∆ϕ y sustituimos dentro de (6.62)
para encontrar:
sin s cos (α + ∆α) = sin  M m ∆ϕ cos ∆λ (6.63)
2 Nm 12 2  2 Nm
 
 2
Las ecuaciones (6.61) y (6.63) son las principales que nos guían a las fórmulas de latitud
media de Gauss. Para derivar la solución inversa dividimos (6.61) por (6.63) para
obtener:
cosϕm sin ∆λ
tan (α12 + ∆2 ) =
α 2 (6.64)
m ∆ϕ cos ∆λ
M 
sin 
2 N 
 m 
2
Nótese que en el problema inverso el lado derecho será una cantidad conocida de tal
forma que la ecuación (6.64) pueda ser usada para encontrar α12 + ∆α / 2 . Conociendo
esta cantidad podemos encontrar s en las ecuaciones (6.61) o (6.63). Por ejemplo, desde
(6.61):
137

147. cos ϕm sin ∆λ
s =
sin 2 N 2 (6.65)
m sin (α12 + ∆α)
2
Con el objeto de encontrar el acimut, el valor de ∆α puede ser calculado desde las
ecuaciones (6.47) o (6.48), que han sido expuestas previamente.
Las fórmulas de la latitud media de Gauss, usualmente se encuentran en forma de series.
Estas pueden deducirse desarrollando en serie las funciones sin ( s / 2 Nm ) , sin ( ∆λ / 2) , y
sin( M m ∆ϕ / 2 N m ) que aparecen en (6.61) y (6.63). Por ejemplo, reteniendo los primeros
términos en (6.61), tenemos:
s sin (α12 + ∆α) = N m cos ϕm ∆λ (6.66)
2
y de la ecuación (6.63):
s cos (α12 + ∆α) = M m ∆ϕ cos ∆λ (6.67)
2 2
Estas ecuaciones pueden ser usadas para resolver el problema directo en una forma
iterativa escribiendo las ecuaciones (6.66) y (6.67) en la forma:
s sin (α + ∆α/ 2)
∆λ = 12
(6.68)
Nm cosϕm
s cos (α12 + ∆α/ 2)
∆ϕ = (6.69)
M m cos ( ∆λ/ 2)
Donde ∆α podría calcularse directamente desde (6.47) o (6.48). Es evidente que la
solución precisa del problema directo, en esta manera, es un procedimiento iterativo.
Una forma de series más completa para la solución del problema inverso han sido dadas
por Lambert y Swick (1935), Bomford (1971, pág. 137) y Lauf (1983, pág.71).
Conociendo la información para el problema inverso, calculamos Nm y Mm. Entonces se
calcula F:
138

148. 1
F = 12 sin ϕm cos 2 ϕm (6.70)
Esencialmente se evalúa (6.48) en la forma:
∆ϕ
∆α = ∆λsin ϕm sec 2 + F∆λ3 (6.71)
Luego se calcula:
∆ϕ' = ∆ϕ (sin ( ∆ϕ/ 2) / ( ∆ϕ/ 2))
∆λ' = ∆λ (sin ( ∆λ / 2) / ( ∆λ / 2))
(6.72)
X 1 = s1 sin( α12 + ∆α) = N m ∆λ' cos ϕm
2
X 2 = s1 cos(α12 + ∆2 ) = M m ∆ϕ' cos( ∆λ / 2)
α
Conociendo X1 y X2 , calcular s1 :
1
s1 = ( X 12 + X 22 ) 2
(6.73)
Finalmente encontramos:
s = s1 ( s1 / 2 N m ) / sin ( s1 / 2 N m )
α12 = tan −1 ( X 1 / X 2 ) − ∆α / 2
(6.74)
α21 = α21 + ∆α ± 180º
La importancia de las fórmulas de la latitud media de Gauss está en la solución del
problema inverso a través de las ecuaciones (6.64) y (6.65), donde no son requeridos
139

149. procedimientos iterativos. La precisión de estas fórmulas es± 1 parte por millón para
líneas de 100 km.
6.5 Las Fórmulas de Bowring
Bowring (1981) dedujo ecuaciones para los problemas directo e inverso para líneas
geodésicas de hasta 150 km de longitud. La derivación en detalle es entregada por
Bowring y no se repetirá aquí. El método usa una proyección conforme del elipsoide en
una esfera, llamada la proyección gaussiana de segunda clase. En esta aplicación, el
factor de escala es tomado en el punto inicial de la línea. Además, la primera y segunda
derivadas del factor de escala con respecto a la latitud, se establecen como cero. La
geodésica desde el elipsoide es entonces proyectada en la línea correspondiente sobre la
esfera donde puede aplicarse la trigonometría esférica.
El procedimiento para la solución directa e inversa no es iterativo usando las ecuaciones
siguientes:
Ecuaciones Comunes
1
A = (1 + e'2 cos 4 ϕ1 ) 2
1
B = (1 + e'2 cos 2 ϕ1 ) 2
1
C = (1 + e' 2 ) 2
(6.75)
w = A(λ2 − λ1 ) / 2
∆ϕ = ϕ2 − ϕ1
∆λ = λ2 − λ1
140

150. Ecuaciones del Problema Directo
σ = sB 2 / ( aC )
 A tan σ sin α12 
λ2 = λ1 + 1 tan −1  
A  B cos ϕ1 − tan σ sin ϕ1 cos α1 
D = 1 sin −1 sin σ cos α − 1 sin ϕ sin α tan w 
  (6.76)
2 
  12
A 1 12 
ϕ2 = ϕ1 + 2 D  B − 3 e'2 D sin  2ϕ1 + 4 BD 
 

 2  3 
 − B sin α 
α2 = tan −1  12 
 cos σ(tan σ tan ϕ1 − B cos α1 ) 
 
Ecuaciones del Problema Inverso
∆ϕ
D = 2 B 1 + 4e' 2 ∆ϕsin  2ϕ1 + 2 ∆ϕ 
3 2 



 B 3  
E = sin D cos w
F = 1 sin w (B cos ϕ1 cos D − sin ϕ1 sin D )
A
(6.77)
E 2
(
tan G = F ; sin σ = E 2 + F 2 )1/2
tan H =  1 (sin ϕ1 + B cos ϕ1 tan D) tan w
A
 

α1 = G − H ; α2 = G + H ± 180º ; s = aCσ / B 2
141

151. Meade (1981) trata la exactitud de esta solución indicando precisiones de 1 ó 2 mm para
la solución directa o inversa en líneas del orden de 120 km de largo. Para líneas de 150
km, el error en la distancia inversa se incrementa hasta 3 ó 4 mm. Para líneas de hasta
100 km, el error acimutal estará en el orden de 0,001” de arco.
6.6 El Método de la Cuerda
Otro procedimiento para resolver el problema inverso y directo es trabajar con l cuerda
a
entre los dos puntos de interés. En las secciones 4.19 y 4.23 tratamos métodos para
trabajar con una cuerda entre dos puntos. En 4.19 consideramos la cuerda y el acimut de
su sección normal entre dos puntos en o sobre el elipsoide. En la sección 4 vimos la
.23
conversión de la extensión de una geodésica o sección normal entre dos puntos, en el
elipsoide, en una cuerda, y viceversa. Ahora aplicamos estas ecuaciones a la solución del
problema directo e inverso.
6.6.1 El Problema Inverso
Conociendo ϕ1 , λ1 , ϕ2 , λ2 , calculamos las coordenadas X, Y, Z, de la ecuación (3.152)
asumiendo que la altura es cero. La distancia de cuerda es:
[
c = ( X 2 − X 1 ) 2 + (Y2 − Y1 )2 + (Z 2 − Z1 )2 ] 1
2
(6.78)
Esta distancia de cuerda puede convertirse en longitud de geodésica usando (4.106) o en
una extensión de sección normal usando (4.107). El acimut de la sección normal puede
ser calculado en forma cerrada usando la ecuación (4.71) donde A es el primer punto. Si
se necesita el acimut geodésico se puede usar una ecuación tal como (4.111). Si se
requiere el acimut inverso puede encontrarse también usando (4.71), adoptando el punto
A como el segundo de los dos puntos.
6.6.2 El Problema Directo
Recordemos que para el problema directo conocemos ϕ1 , λ1 , α12 y s. Por conveniencia
establecemos λ1 = 0 y resolvemos para una diferencia de longitud con respecto al primer
punto. En este caso, las coordenadas rectangulares del primer punto son (tomando 3.152):
142

152. X 1 = N1 cos ϕ1
Y1 = 0 (6.79)
Z1 = N1 (1 − e ) sin ϕ1
2
Las diferencias de coordenadas serían:
∆X = X 2 − X 1
∆ Y = Y2 (6.80)
∆Z = Z 2 − Z 1
Ahora invertimos (4.67) y al mismo tiempo establecemos λ = 0 . Encontramos:
 ∆X   − sin ϕ1 0 cos ϕ1  u 
     
 ∆Y  =  0 1 0  v  (6.81)
     
 ∆Z   cos ϕ1 0 sin ϕ1   w
donde las coordenadas locales son (ver 4.60):
u = c cos V cos α12
v = c cos V sin α12 (6.82)
w = c sin V
Sustituyendo (6.82) en (6.81) tenemos:
∆X = − c (sin ϕ1 cos V cos α12 − sin V cos ϕ1 )
∆Y = c cos V sin α12 (6.83)
∆Z = c (cos ϕ1 cos V cos α12 + sin ϕ1 sin V )
143

153. Conocemos c y α12 al lado derecho de (6.83). Asumiendo que conocemos V, podemos
usar (6.83) para hallar ∆X , ∆Y , ∆Z . Entonces calculamos las coordenadas rectangulares
del segundo punto.
X 2 = X 1 + ∆X
Y2 = ∆ Y (6.84)
Z 2 = Z 1 + ∆Z
Conociendo estas coordenadas podemos calcular la latitud y longitud desde (como se
discutirá en la sección 6.8):
Z2
tan ϕ2 = (6.85)
( )( )
1
1 − e2 X2 + Y
2 2
2
2
Y
tan ∆λ = X2 (6.86)
2
Estas ecuaciones completarían la solución del problema directo.
Al resolver (6.83) asumimos conocer V. Este ángulo V es el negativo del ángulo de
declinado tratado en la sección 4.17. Por ejemplo, desde (4.52) podemos escribir:
2 N1
( )
− V = s 1 + η12 cos 2 α12 − s 2 η12 t 1 cos α12
2
2 N1
(6.87)
De la Figura 6.5 puede deducirse un valor simplificado para V, asumiendo que los dos
puntos están en una esfera, cuyo radio es el radio ( Rα ) de curvatura en la dirección de la
línea.
144

154. µ
c/2 c/2
Rα
µ
Figura 6.5 Determinación Aproximada del Ángulo de Declinación
Tenemos:
sin µ = sin ( −V ) = 2 c (6.88)
Rα
El uso de (6.88) o aun de (6.87) podría crear un error pequeño en las coordenadas
calculadas. Si las coordenadas rectangulares son las correctas, tiene que satisfacerse la
ecuación de la elipse. Específicamente, desde (3.153) deberíamos tener:
1
 X 2 + Y 2 + Z22  2
 2 −a= 0 (6.89)

2 (1−e2 ) 

Si V no es correcto, el lado derecho igualará (digamos) a h. Conociendo h se puede
calcular una corrección para V (Vincenty, 1977) como sigue:
− dV = h (6.90)
c cos V
El ángulo vertical corregido podría ser:
145

155. Vi +1 = Vi + dV (6.91)
Lo cual puede ser usado en (6.83) para obtener valores mejorados de ∆X , ∆Y , ∆Z .
Después que el ciclo iterativo haya convergido (por ejemplo h ≤ 1 mm ) se puede usar el
juego final de valores para X 2 , Y2 , Z 2 en (6.85) y (6.86) para obtener la latitud y
longitud del segundo punto.
6.7 Exactitud de los Métodos Directo e Inverso para Líneas de Longitud
Mediana
En las secciones previas hemos tratado varios métodos para r
esolver el problema directo
e inverso. Cada método tenía aproximaciones asociadas a truncamiento de series o
aproximaciones geométricas. En algunos casos hemos citado pautas respecto de la
exactitud de las ecuaciones. Pero se pueden obtener estimaciones más específicas de
precisión si se calcula una serie de líneas de prueba con el juego de fórmulas más
precisas, haciendo comparaciones con los resultados para los métodos aproximados.
Tales cálculos han sido desarrollados por Gupta (1972) para varios métodos y Badi
(1983) para el método de Bowring.
Antes de hablar sobre las precisiones de cada método deberíamos poner en contexto las
precisiones que podríamos desear en el cálculo de la posición. Por ejemplo, recordemos
primero que 1” de arco corresponde a ≈ 30 m en la superficie del elipsoide. Tenemos
entonces:
________Medida de Arco___________________________Medida Lineal________
1" 30 m
0,1" 3m
0,01" 0,3 m = 30 cm
0,001" 0,03 m = 3 cm
0,0001" 0,003 m = 0,3 cm = 3 mm
0,00001" 0,0003 m = 0,03 cm = 0,3 mm
___________________________________________________________________
146

156. Si nos dieran un juego de latitudes y longitudes, nos gustaría que cualquier distancia
calculada de aquel fuera la correcta (para propósitos de estabilidad) a 1 mm. Esto
implicaría que las ϕ y λ debieran darse con una exactitud del orden de 0,00001”. Hay
muchos casos en donde un criterio tan riguroso puede ser relajado dependiendo de la
aplicación de los resultados.
Las pruebas realizadas por Gupta constaron de líneas de diferentes extensiones y acimut,
y latitud del primer punto. En la mayoría de los casos, hay una sensibilidad a los
resultados dependiendo de estas tres cantidades. Aquí no se presenta un listado completo
de los resultados. Basta tabular la distancia máxima en los acimut y latitudes más
deficientes, para los cuales las ecuaciones específicas producen la exactitud dada. Tales
resultados se dan en la tabla siguiente:
Extensión Máxima de Línea para la cual una Solución Directa Conocida Logra la Exactitud Dada
(Distancias en km)
___________________________________________________________________
0,00001" 0,0001" 0,001" 0,01"
Series Legendre (4 términos) 30 40 80 100
Series Legendre (5 términos) 60 90 100 200
Puissant (corto, (6.51)) 10 10 10 10
Puissant (largo, (6.40)) 10 20 40 80
Bowring (Cuerda) 70 100 300 700
___________________________________________________________________
La precisión más deficiente en estos resultados usualmente ocurre en las altas latitudes.
(La latitud más alta usada en esas pruebas fue de 70º). Por ejemplo, para una latitud de
10º, a distancia máxima para la serie de Legendre, con derivadas del quinto orden, es de
l
100 km para una exactitud de 0,00001" en lugar de 60 km dados en la tabla.
De esos resultados concluimos que las fórmulas de Bowring para el problema directo
producen la mejor precisión de las ecuaciones aquí descritas.
La exactitud del problema inverso puede describirse de manera similar. En la tabla
siguiente comparamos los errores de distancia y acimut para las fórmulas de latitud media
de Gauss y de Bowring. De nuevo hemos escogido errores máximos que dependen del
acimut y de la latitud.
147

157. Error Máximo en la Solución del Problema Inverso para Líneas de Varias Extensiones
Largo de la Línea Latitud Media de Gauss Bowring
Km Acimut (”) Distancia (mm) Acimut (”) Distancia (mm)
50 0,0048" 4 0,0003” 0,1
100 0,020" 33 0,0024” 1,1
200 0,083" 136 0,0049 9,7
Los resultados de Bowring claramente son los mejores. Los errores son aún bastante
sensibles a la latitud y al acimut. Para una extensión de 100 km y 0º de acimut, el error en
las fórmulas Bowring en 10º de latitud es 0,08 mm, aumentando a 1,1 mm en 40º.
6.8 El Problema Inverso para las Coordenadas Rectangulares Espaciales
Conociendo ϕ, λ y h de un punto, calculamos las coordenadas rectangulares espaciales
como sigue (ver 3.152):
X = ( N + h ) cos ϕ cos λ
Y = ( N + h) cos ϕsin λ (6.92)
Z = ( N (1 − e 2 ) + h) sin ϕ
Ahora examinamos el cálculo de ϕ, λ, h, conociendo X , Y , Z y los parámetros del
elipsoide. La solución no es directa debido a que N es función de la latitud. Se han
presentado varias soluciones iterativas y de forma cerrada para este problema. Primero
consideramos una solución iterativa sugerida por Hirvonen y Moritz (1963).
Para hacerlo, primero hallamos la longitud dividiendo la Y por la ecuación X de (6.92):
tanλ = Y (6.93)
X
Luego consideramos la siguiente sección meridiana que es mostrada en la Figura 6.6:
148

158. h
(N + h)
(N + h)sinϕ
ϕ
ϕ
(X2 + Y2 )1/2
Figura 6.6 Sección de Meridiano Mostrando un Punto sobre el Elipsoide
Tenemos:
( N + h) sin ϕ
tan ϕ = (6.94)
X 2 +Y 2
Ahora Z = N sin ϕ − e 2 N sin ϕ + h sin ϕ ó ( N + h ) sin ϕ = Z + e 2 N sin ϕ , entonces:
Z + e2 N sin ϕ
tan ϕ = (6.95)
X 2 +Y 2
Necesitamos resolver esta ecuación por iteración, por tanto primero escribimos:
149

159. tan ϕ = Z 1 + e 2 N sin ϕ (6.96)
X 2 + Y2 
 Z 

Si, como primera aproximación, tomamos h = 0, Z = N (1 − e 2 ) sin ϕ , la ecuación (6.96)
puede ser escrita como:
tan ϕ1 = Z
X +Y
2 2
[
1+ e 2
2
1−e
]
ó (6.97)
tan ϕ1 = 1 ⋅ Z
1−e2 X +Y 22
Esta ecuación es exacta cuando h = 0, y puede ser usada para obtener una primera
aproximación para la latitud deseada. Con esta aproximación la ecuación (6.95) puede ser
iterada para encontrar su convergencia.
De las primeras dos ecuaciones de (6.92) podemos encontrar h:
X 2 +Y 2
h= cos ϕ − N (6.98)
De la tercera ecuación de (6.92) tenemos:
h= Z − N + e2N (6.99)
sin ϕ
La selección entre el uso de (6.98) o (6.99) depende de la latitud aproximada. En las
regiones polares (6.99) debería ser más estable que (6.98), mientras que lo opuesto sería
verdadero en las regiones ecuatoriales.
En 1976 Bowring describió un procedimiento iterativo que converge más rápido que el
recientemente expuesto. (Ver Figura 6.7). Consideremos una elipse de meridiano con el
punto Q ubicado en alguna elevación sobre el elipsoide, siendo P el punto
correspondiente en el elipsoide. Permítase que C sea el centro de curvatura de la elipse
meridiana en el punto P. La distancia CP es el radio de curvatura del meridano, M.
150

160. Z
Q
h
P
M
ϕ
X
C
Figura 6.7 Elipse Meridiana para la Derivación de Bowring
La coordenada x de C es:
x C = xP − M cos ϕ (6.100)
Usando (3.42) para x P y (3.88) para M, (6.100) se reduce a
a e 2 cos 3 ϕ
xC = (6.101)
W3
Usando (3.66) esto se convierte en:
x C = a e 2 cos 3 β (6.102)
De manera similar calculamos la coordenada z de C. Encontramos:
151

161. z C = − e' 2 b sin 3 β (6.103)
De la figura 6.7 vemos que:
zQ − zC
tan ϕ =
x Q − xC
o sustituyendo para xC y zC, tenemos:
z Q + e' 2 b sin 3 β
tan ϕ = (6.104)
xQ − ae 2 cos 3 β
En términos de X, Y, Z, podemos escribir (6.104) como:
Z + e' 2 b sin 3 β
tan ϕ = i (6.105)
X 2 + Y 2 − ae 2 cos 3 β
La ecuación (6.105) es la ecuación básica que ha de iterarse para la solución de Bowring.
El valor inicial aproximado de β puede ser encontrado de (3.28) y (3.29):
a Z
tan β0 =
(
b X +Y2
2
)
1/ 2
(6.106)
Cualquier valor actualizado de β que se necesite puede ser calculado de (3.63):
tanβ = (1 − f ) tanϕ (6.107)
donde ϕ se calculará de (6.105).
152

162. Para aplicaciones terrestres, todo lo que se necesita es un ciclo iterativo único de (6.105)
comenzando con (6.106) para obtener resultados precisos m ejores de 0,1 mm. En alturas
de 5000 m, el error de tal cálculo podría alcanzar 39 mm, lo cual podría eliminarse con
otra iteración.
La altura podría determinarse de (6.98) o (6.99). Sin embargo, una manera más
conveniente para cualquier técnica fue sugerida por Bartelme y Meissl (1975) como parte
de su derivación para otro procedimiento en la determinación de ϕ, λ, y h. Comenzamos
con la elipse meridiana y un círculo pasando a través del punto de interés, según es
mostrado en la Figura 6.8.
z
(X2 +Y2 )1/2 = p p
h
a cosβ
p’ z
b sinβ
Figura 6.8 Geometría para la Determinación de h
Usando (3.28) y (3.29) vemos que en el elipsoide las coordenadas x y z de p’ son a cos β
y b sin β . Tenemos:
h 2 = ( p − a cos β) 2 + ( z − b sin β) 2 (6.108)
El signo de h es asignado igualando el signo del primer término en paréntesis. Se
recomienda el uso de la ecuación (6.108) para el cálculo de alturas por razones de
simplicidad y estabilidad, aunque ésta fallará si el punto se ubica en uno de los polos.
Vincenty (1980 a) sugirió una mejora del procedimiento Bowring introduciendo un
elipsoide auxiliar que pasa a través del punto que está siendo transformado. Este método
es especialmente útil cuando una elevación es aproximadamente conocida o es calculada
de una manera aproximada.
153

163. Varios autores han propuesto fórmulas cerradas para la evaluación de ϕ, λ y h a partir de
X, Y y Z (por ejemplo, Paul, (1973) y Heikkinen, 1982)). Los pasos de cálculo para el
procedimiento de Heikkinen son:
r = X 2 +Y 2
F = 54b 2 Z 2
G = r 2 + (1 − e 2 ) Z 2 − e 2 E 2 ; ( E 2 = a 2 − b 2 )
e 4 Fr 2
c=
G3
s= 3
1 + c + c 2 + 2c
P= F
3( s + s
1 + 1)2 G 2
Q = 1 + 2e 4 p
P (1 − e 2 ) Z 2 Pr 2
r0 = −Pe r + a (1 + 1 ) −
2
−
2
1+Q 2 Q Q(1 + Q) 2
U = ( r − e 2 r0 ) 2 + Z 2
V= ( r − e 2 r0 ) 2 + (1 − e 2 ) Z 2
z0 = b Z
2
aV
154

164. b2
h = U (1 − aV )
Z + e'2 z0
tan ϕ = r
Y
tan λ =
X
Cualquier error en la aplicación de esas ecuaciones podría emanar de situaciones
inestables. Aparentemente, las fórmulas de Heikkinen son estables (Vincenty, 1982
comunicación privada).
En términos de tiempo de evaluación del cálculo, la técnica anterior es la más lenta. Si
permitimos que el tiempo para este enfoque sea 1, el tiempo para el enfoque Bowring
sería 0,73, para el de Vincenty (1980) 0,66 y para el de Hirvonen-Moritz 1,05.
155

165. 7 INFORMACIÓN ASTROGEODÉSICA
7.1 Coordenadas Astronómicas
Hasta aquí, hemos considerado las coordenadas geodésicas que son definidas con
respecto a un sistema específico de ejes y planos implicados por dichos ejes. Se
tiene la medida de latitud considerando el plano ecuatorial, el cual es
perpendicular al eje z de rotación del elipsoide. La longitud geodésica es el
ángulo entre un meridiano inicial (conteniendo los ejes x y z) y el meridiano que
pasa a través del punto de interés.
En el mundo real donde las mediciones son realizadas con respecto a la dirección
del vector gravedad, en un punto sobre la superficie de la tierra, no podemos
determinar directamente la latitud geodésica, longitud, acimut de la sección
normal, ángulo vertical, etc., considerando que el plano horizontal de los
instrumentos usado para esas mediciones son orientados para que el plano
horizontal del instrumento quede perpendicular a la dirección de la gravedad. Las
cantidades medidas con respecto a la orientación del vector gravedad son
generalmente llamadas cantidades astronómicas. Tenemos latitud astronómica,
longitud astronómica, acimut astronómico, ángulo vertical astronómico, o
distancia cenital astronómica. Con el objeto de definir tales cantidades es
necesario definir un sistema de coordenadas y planos iniciales para referenciar
(por ejemplo) la latitud y la longitud astronómica. Las definiciones de estos
sistemas están ampliamente ligadas a las observables relacionadas con la Tierra
física.
No es la intención de este trabajo adentrarse en los detalles de las definiciones de
los sistemas de coordenadas astronómicos. Tal enfoque puede ser encontrado en
Mueller (1969, pág. 19), Bonford (1980, pág. 97), Vanicek y Krakiwsky (1982,
pág. 296), Mueller (1981, pág. 9), etc. Es importante para nosotros, sin embargo,
resumir algunas definiciones y aplicaciones apropiadas.
El eje Z usado para propósitos de referenciación astronómica es relacionado con
el eje de rotación de la Tierra. Tal eje requiere una definición precisa,
considerando que el eje de rotación instantáneo no permanece fijo en posición
con respecto a la corteza de la Tierra. Las primeras observaciones del movimiento
del polo fueron iniciadas en 1899 usando la latitud definida de cinco estaciones
del servicio de latitud i ternacional. Los datos de esas estaciones han sido usados
n
para definir el Origen Internacional Convencional (CIO), el cual es el polo
terrestre promedio desde el año 1900 al 1905. Los valores del movimiento polar
156

166. también han sido determinados por el Servicio de Movimiento Polar
Internacional (IPMS) el que usa datos provenientes de un gran número de
observatorios, y del Bureau International de l’Heure (BIH). Los cambios en el
movimiento polar ahora son obtenidos rutinariamente desde el análisis del
movimiento de satélites. Cada determinación del movimiento polar podría ser un
tanto diferente dependiendo de los catálogos de estrellas usado, coordenadas
adoptadas por la estación, procedimientos de observación, constantes adoptadas,
etc. En el futuro cercano, mejoras en la determinación del movimiento polar y del
eje Z serán posible usando nuevos y mejores procedimientos de observación y
técnicas de procesamiento. Debería estar claro que las determinaciones del
movimiento polar desde 1899 no tienen una precisión uniforme ni un eje Z de
referencia uniforme.
En adelante asumiremos que tenemos un eje Z el cual es llamado Sistema
Terrestre Convencional (CTS) (Mueller, 1981). El eje de rotación instantáneo es
localizado con respecto al eje Z por los elementos del m ovimiento polar x p , yp . La
latitud astronómica de un punto, en la superficie de la Tierra, debería ser el
ángulo medido entre el ecuador (perpendicular al eje de rotación medio) y la
dirección del vector gravedad en el punto de interés. La latitud astronómica media
(Φ M) puede ser obtenida desde la latitud astronómicas instantánea (Φ I) (esto es
con respecto al ecuador instantáneo) usando las coordenadas (x p , yp ) del polo
instantáneo con respecto al polo de referencia usado (Mueller, 1969, pág. 87):
Φ M = Φ I + y P sin Λ − x P cos Λ (7.1)
Para definir la longitud astronómica instantánea primero definimos el plano
meridiano astronómico instantáneo como el “plano que contiene la normal
astronómica en P paralela al eje de rotación instantáneo de la tierra” (Mueller,
1969, pág. 19). El meridiano astronómico medio será aquel plano que contenga la
normal astronómica en P, y que es paralelo al eje Z del Sistema Terrestre
Convencional. La longitud astronómica es el ángulo entre el meridiano inicial
(hoy en día definido por el BIH) y el meridiano astronómico que pasa a través del
punto de interés. Valores de la longitud astronómica media (ΛM) pueden ser
Λ
obtenidos desde la longitud astronómica instantánea ( I) a través de la aplicación
de la corrección del movimiento polar (Mueller, 1969, pág. 87):
Λ M = Λ I − ( x P sin Λ + y P cos Λ) tan Φ (7.2)
El primer acuerdo sustancial en la definición del meridiano inicial fue alcanzado
en la Conferencia del Meridiano Internacional que se efectúo en octubre de 1884,
Washington (Howse, 1980). Entonces el meridiano inicial fue definido como
157

167. “aquel que pasa por el centro del instrumento de tránsito en el Observatorio de
Greenwich”. Desde ese tiempo, definiciones mejoradas han sido adoptadas. Con
variadas definiciones realizadas en diferentes tiempos es claro que la longitud
astronómica considerada sobre un extenso periodo de tiempo podría no constituir
un juego de datos homogéneos. En Estados Unidos, las longitudes astronómicas
fueron originalmente ligadas a una longitud definida en el Observatorio Naval de
EE.UU. Sin embargo, esta longitud y los catálogos de estrellas usados desde 1922
fueron inconsistentes con aquel usado por el Bureau International de l’Heure
(BHI). Petty y Carter (1978) estimaron un promedio para la corrección de
longitud de –0,50” (positivo en longitud oeste) para la determinación de
longitudes astronómicas en EE.UU. previas a 1962. Esta corrección dependiente
del tiempo es llamada la corrección del observatorio y debería ser aplicada a las
longitudes astronómicas publicadas por el National Geological Survey previas a
1978 (Petty, comunicación privada, 1981).
Hoy día los ejes iniciales (X, Z) son definidos por un determinado juego de
longitudes astronómicas en aproximadamente 50 observatorios de tiempo
desplegados alrededor de la Tierra que envían los datos al BHI en París. Tales
mediciones permiten la definición precisa de un meridiano inicial el cual ahora no
es físicamente observable en Greenwich. En la práctica, las correcciones del
movimiento polar son aplicadas para obtener un meridiano inicial “medio”.
Un acimut astronómico es al ángulo entre el norte astronómico (o el plano
meridiano astronómico) y el plano que contiene el vector gravedad en el punto de
observación que pasa a través del punto observado.
Debido a que el plano astronómico puede variar como consecuencia de las
variaciones en los ejes de rotación descritos por el movimiento polar, deberíamos
hablar de un acimut astronómico instantáneo (AI) y un acimut astronómico medio
(AM). Los dos acimut son relacionados como sigue (Mueller, 1969, pág. 88):
AM = AI − ( x P sin Λ + y P cos Λ) sec Φ (7.3)
En subsecuentes tratados nos referiremos solamente al acimut astronómico
medio. Este será medido desde el norte en el sentido de los punteros del reloj.
La distancia cenital astronómica (Z’) es el ángulo subtendido desde el cenit,
definido por la dirección del vector gravedad, en dirección hacia el punto que está
siendo observado.
Arriba hemos considerado mediciones astronómicas referidas a la dirección del
vector gravedad en un punto sobre la superficie de la Tierra. Para aplicaciones
que comprometen coordenadas astronómicas y geodésicas (ver las secciones
158

168. siguientes) es importante que las coordenadas astronómicas sean reducidas al
elipsoide o en la práctica al geoide. Para llevar a cabo ésto deben efectuarse
correcciones por curvatura de la línea de plomada, según lo describe Heiskanen y
Moritz (1967, pág. 193).
La Figura 7.1 identifica varias cantidades con respecto a los ejes del Sistema
Terrestre Convencional.
ZCTS
Cenit
Astronómico
Norte
Astronómico
z’
# Este
A
Eje Z Vector
Paralelo Gravedad
Meridiano
Astronómico
Plano del
Meridiano Φ
Inicial Λ
Figura 7.1 Cantidades Astronómicas Medidas
7.2 Comparación de Cantidades Angulares Astronómicas y Geodésicas
Cantidades astronómicas y geodésicas tales como latitud, longitud, acimut y
distancia cenital principalmente se diferenciarán porque tales cantidades son
medidas respecto de una dirección cenital diferente. Las cantidades astronómicas
son medidas con respecto a un cenit definido por la dirección del vector gravedad,
mientras que las cantidades geodésicas son definidas con respecto al cenit
definido por una normal al elipsoide.
159

169. Es posible también que las coordenadas difieran por el uso de diferentes polos de
referencia y diferentes meridianos iniciales para los sistemas astronómicos y
geodésicos. Idealmente nos gustaría que estos sistemas fuesen lo mismo, pero en
realidad ésto no podría ser.
Para nuestra primera revisión analítica de las diferencias entre las coordenadas,
supondremos, no obstante, que los ejes de rotación de la referencia astronómica y
geodésica son paralelos. También supondremos que las longitudes y mediciones
desde los meridianos iniciales son paralelos. Esta derivación sigue la efectuada
por Heiskanen y Moritz (1967, pág. 184).
Ahora consideraremos una esfera unitaria relacionada con un punto A en la
superficie de la Tierra como se muestra en la F igura 7.2. La intersección del eje
de rotación del elipsoide con la esfera es designado P. (Note que hay solo un
polo, ya que hemos asumido que los ejes de rotación astronómicos y geodésicos
son paralelos). La normal al elipsoide que pasa a través de A intersecará a la
esfera en ZG, el cenit geodésico en A. Ahora extendemos la dirección del vector
gravedad en A de tal modo que interseque la esfera auxiliar en ZA lo cual es
denominado cenit astronómico en A. Permitamos que m sea el punto de
intersección de la línea de la visual y la esfera unitaria cuando el teodolito
(nivelado respecto del vector gravedad) es apuntado a un objetivo M. Los puntos
ZG y ZA son conectados a los punto P y m por círculos máximos. El arco m A esZ
la distancia cenital medida hasta el punto M y es denominada z’. El plano AZAm
es el plano vertical en el punto A que pasa por M. El arco m G es la distancia
Z
cenital geodésica y es designada como z. El plano A Gm es el plano de la sección
Z
normal directa desde A hasta M medida con respecto a la normal elipsoidal que
pasa por A. Notamos que el arco ZAP es 90°- Φ. El plano A GP del meridiano
Z
geodésico en A. El plano AZAP es el plano del meridiano astronómico en A. El
ángulo ZGPZA = (∆l ) es el ángulo entre los meridianos astronómico y geodésico
en A. Asumiendo que las longitudes astronómica y geodésica son calculadas
desde el mismo meridiano inicial, tenemos:
∆l = Λ − λ (7.4)
También permitamos que el arco ZGZA sea θ lo cual es la deflexión total de la
vertical en el punto A. El ángulo PZGZA es el acimut geodésico del plano (γ)
AZGZA que contiene la deflexión total de la vertical en A. El acimut astronómico
correspondiente del plano AZGZA es γ’.
160

170. ZG ξ
Z
γ 90°- ϕ- ξ
α
R η
θ
ZA Λ- λ
z γ’ P
α 90° - ϕ
R’
z’ T
M
q
m
A
Figura 7.2 La Esfera Celeste Mostrando Cantidades Astronómicas y Geodésicas
Dibujamos el arco ZAZ2 desde ZA perpendicular al meridiano geodésico PZG.
Entonces el arco ZGZ2 es ξ el cual es la componente de la deflexión total a lo
largo del meridiano. El arco ZAZ2 es η el cual es la componente de la deflexión
total de la vertical en la dirección del primer vertical.
El acimut (sección normal) geodésico del plano A Gm es el ángulo P Gm el cual
Z Z
es designado α. El ángulo P Am designado A es el acimut astronómico del plano
Z
AZAm.
Desde el triángulo esférico derecho ZAZ2 P tenemos:
cos (Λ − λ) = tan Φ cot (ϕ + ξ ) (7.5)
sin η = sin ( Λ − λ) cos Φ (7.6)
161

171. Puesto que η y (Λ - λ) son ángulos pequeños y ϕ ≈ Φ, podemos escribir la
ecuación (7.6) como:
η = (Λ − λ) cos ϕ (7.7)
ó
(Λ − λ) = η sec ϕ (7.8)
Asumiendo que cos (Λ − λ) = 1 en la ecuación (7.5) podemos mostrar que:
Φ −ϕ = ξ (7.9)
Las ecuaciones (7.7), (7.8) y (7.9) son las ecuaciones básicas que expresan las
componentes ξ y η de la deflexión de la vertical en términos de coordenadas
astronómicas y geodésicas.
Ellas son válidas solamente cuando los aspectos asumidos sobre el polo
astronómico y geodésico, y los meridianos iniciales son válidos. Los valores de ξ
y η definidos por esas ecuaciones son llamados deflexiones astrogeodésicas de la
vertical. En consideración a que las coordenadas geodésicas dependerán de las
dimensiones del elipsoide de referencia, y más generalmente, del datum
geodésico usado para referenciar las coordenadas geodésicas, las deflexiones
astrogeodésicas son cantidades dependientes del datum (geodésico).
Otras relaciones interesantes podrían ser derivadas del triángulo ZGZAZ2 .
Considerando el triángulo como si fuese plano podemos escribir:
ξ = θ cos γ
η = θ sin γ
(7.10)
η
tan γ =
ξ
ξ η
θ= = = ξ2 + η2
cos γ sin γ
162

172. Si es necesario podríamos sustituir expresiones para ξ y η dentro de la ecuación
(7.10).
Seguidamente consideramos la relación entre el acimut astronómico A y el
acimut geodésico α. Para hacerlo primero designamos el ángulo m GZA como R y
Z
el ángulo mZAT como R1 . Entonces:
α = R +γ
(7.11)
A = R1 + γ '
Desde el triángulo ZGZAP en el cual el ángulo en ZA es 180°- γ’, tenemos:
− cos γ ' = − cos γ cos( Λ − λ) + sin γ sin ( Λ − λ) sin ϕ (7.12)
Asumiendo cos (Λ − λ) = 1, sin ( Λ − λ) = ( Λ − λ) , la ecuación (7.12) puede ser
escrita como:
cos λ − cos γ ' = ( Λ − λ) sin γ sin ϕ (7.13)
Si sustituimos la ecuación (7.8) dentro de (7.13) obtenemos:
cos γ − cos γ ' = ηtan ϕsin γ (7.14)
Ahora podemos usar las identidades trigonométricas dadas en la ecuación (5.12),
por tanto tenemos:
cos γ − cos γ ' = −2 sin
1
(γ + γ ')sin 1 (γ − γ ') = ηtan ϕsin γ (7.15)
2 2
Dejando
1
(γ + γ ') = γ y sin 1 (γ − γ ') = (γ − γ ') , tenemos:
2 2 2
163

173. γ '−γ = ηtan ϕ
ó (7.16)
(
γ '−γ = (Λ − λ) sin ϕ = ( Λ − λ) cos 90 − ϕo
)
Ahora el triángulo esférico mZGZA es similar al triángulo ZGZAP en el sentido
siguiente: el vértice P corresponde al vértice m, el ángulo q (en m) corresponde al
ángulo (Λ − λ) y los lados z’ y z corresponden a los lados 90°-Φ y 90°- Φ- ξ, γ’
corresponde a R1 y γ a R. Con esta analogía la última ecuación de (7.16) puede ser
reescrita:
R1 − R = q cos z ' (7.17)
Desde el triángulo mZGZA, tenemos:
sin R
sin q = sin θ (7.18)
sin z '
Puesto que q y θ son pequeños, sin q ≈ q , y sin θ ≈ θ , la ecuación (7.18) podría ser
usada en (7.17) para escribir:
θ sin R
R1 − R = (7.19)
tan z '
Agregando las ecuaciones (7.16) y (7.19) tenemos:
θ sin R
( R1 − R) + (γ '−γ ) = + ηtan ϕ (7.20)
tan z '
Diferenciando las ecuaciones de (7.11) encontramos:
A − α = ( R1 − R) + (γ '−γ ) (7.21)
Ahora permitamos que R = α − γ de tal forma que podamos usar la ecuación
(7.20) en la ecuación (7.21) para escribir:
164

174. θ sin (α − γ )
A − α = ηtan ϕ + (7.22)
tan z '
Expandiendo el seno en la diferencia de ángulos, queda:
θsin αcos γ − θ cos αsin γ
A − α = ηtan ϕ + (7.23)
tan z '
Usando la ecuación (7.10) podríamos sustituir θcos γ yθsin γ , y tomando z’ = z,
podemos escribir:
ξsin α − ηcos α
A − α = ηtan ϕ + (7.24)
tan z
La ecuación (7.24) también podría ser expresada de la forma siguiente:
A − α = ( Λ − λ) sin ϕ + (ξsin α − ηcos α) cot z (7.25)
Esta ecuación nos da la relación entre el acimut astronómico y geodésico como
función de la deflexión astrogeodésica de la vertical. En muchas redes de
triangulación z ≈ 90 o de modo que cot z ≈ 0 , y el último término en la ecuación
(7.25) es despreciable. En este caso la ecuación (7.25) es escrita en una forma
más familiar:
A − α = ηtan ϕ = (Λ − λ) sin ϕ (7.26)
Dado Λ , λ, A,ϕ podríamos usar la ecuación (7.26) para calcular α, el acimut
geodésico de la línea. De (7.26) tenemos:
α = A − (Λ − λ) sin ϕ (7.27)
La ecuación (7.26) y (7.27) son conocidas como las ecuaciones de Laplace. El
acimut geodésico calculado desde la ecuación (7.27) es llamado el acimut de
Laplace.
165

175. Escribiendo (7.25) en la forma de (7.27) obtenemos la ecuación de Laplace
“extendida”.
α = A − ( Λ − λ) sin ϕ − (ξsin α − ηcos α) cot z (7.28)
o sustituyendo ξ y η usando (7.10)
α = A − sin αcot z (Φ − ϕ) − (sin ϕ − cos ϕcos αcot z )( Λ − λ) (7.29)
Con el objeto de calcular el acimut de Laplace es necesario observar el acimut y
longitud astronómico de un punto dado y disponer de la longitud geodésica.
(Veremos luego que un valor exacto de λ no es necesario, puesto que la ecuación
de Laplace será usada en un ajuste de datos geodésicos). Las estaciones desde
donde se efectúan tales observaciones son llamadas estaciones de Laplace. Tales
estaciones han sido establecidas en la mayoría de las redes de triangulación. El
espaciamiento de tales estaciones puede variar desde 10 hasta 300 km.
dependiendo del tamaño de la red y la intención en la precisión de los resultados.
El propósito principal de incluir un acimut de Laplace en una red geodésica es
proveer la orientación acimutal de la red, de tal modo que los errores de
orientación sean distribuidos uniformemente en la red. Adicionalmente, el uso de
las ecuaciones como (7.28) tienden a reforzar la condición de las suposiciones
hechas en la derivación de la ecuación de Laplace; esto es, el paralelismo de los
ejes polares y el paralelismo del meridiano inicial (Moritz, 1978, pág. 68).
En las redes geodésicas que están siendo desarrolladas hoy en día y en el futuro
se ha visto reducida significativamente la necesidad de los acimut de Laplace,
debido a la incorporación de determinación de posiciones mediante satélites
dentro del ajuste de la red. Tales determinaciones proveen información de
orientación y de escala que (con un espaciamiento apropiado entre las estaciones)
refuerzan la red geodésica. La incorporación de tales posiciones dentro de la red
es tratada por Moose y Henriksen (1976), Asquenazí (1981), Vincenty (1982) y
muchos otros.
Uno de los últimos efectos que requiere ser considerado, es la discrepancia entre
las distancias cenitales astronómicas y geodésicas. Para ello consideremos el
triángulo mZGZA, como se muestra en la Figura 7.3, donde el arco ZGZ’ es
perpendicular a mZA. Entonces la diferencia deseada z’-z será el arco ZAZ’.
166

176. ZG
z
ZA
Z’ R1
m
z’
Figura 7.3 Determinación de las Distancias Cenitales
Considerando el Triángulo ZGZAZ’ como un triángulo plano, tenemos:
Z A Z ' = θ cos(180 − R1 ) = −θ cos R1 (7.29)
usando R1 de la ecuación (7.11) y observando que A − γ ' ≈ α − γ
Z A Z ' = −θ cos ( A − γ ') ≈ −θ cos(α − γ ) (7.30)
o expandiendo cos (α − γ ) :
Z A Z ' = −θ cos αcos γ − θ sin αsin γ (7.31)
usando la ecuación (7.10) podríamos escribir (7.31) como:
Z A Z ' = z '− z = −(ξcos α + ηsin α) (7.32)
El término (ξcos α + ηsin α) es el componente de la deflexión de la vertical en la
dirección α. Con la ecuación (7.32) podemos convertir una distancia cenital dada
z’, en una distancia cenital geodésica z. Este procedimiento es necesario cuando
las alturas están siendo obtenidas mediante nivelación trigonométrica.
167

177. 7.2.1 Corrección de Direcciones por Efectos de la Deflexión de la Vertical
En una red de triangulación los ángulos horizontales son medidos con respecto a
la dirección del vector gravedad en el punto. Lo que se desea para las
aplicaciones actuales son las direcciones correspondientes con respecto a la
normal elipsoidal que pasa a través del punto. Esto requiere una corrección a las
direcciones observadas, la cual dependerá de las deflexiones de la vertical.
Para derivar esta corrección consideraremos la ecuación (7.28) l que es derivada
a
para los acimuts. El término − ( Λ − λ) sin ϕ es constante en un punto dado, puesto
que este depende solamente de Λ, λ y ϕ, y es independiente de la dirección. Este
término expresa la influencia sobre el acimut de la no-coincidencia de los planos
de meridianos astronómico y geodésico. El segundo término
− (ξsin α − ηcos α) cot z expresa la influencia en las direcciones medidas de la
no-coincidencia del eje vertical del instrumento y la normal de la superficie
elipsoidal. Esto podría s considerado como una corrección debido a la deflexión
er
del eje vertical del instrumento desde la normal a la superficie del elipsoide de
referencia dado.
Sea D la dirección corregida y D’ la dirección observada. Podemos escribir:
D = D'+δ (7.33)
donde
δ = −(ξsin α − ηcos α) cot z (7.34)
En muchos esquemas de triangulación hemos notado que cot z podría ser cercano
a cero y por tanto la corrección δ será despreciable. En áreas montañosas z podría
alcanzar 60° de tal modo que δ podría alcanzar varios segundos de arco.
Es claro que para calcular la dirección de la corrección se necesitan valores de ξ y
η. La forma más directa es realizar mediciones astronómicas en todos los sitios de
la triangulación. Sin embargo, esto puede resultar demasiado oneroso en términos
de tiempo y horas hombre, por lo cual técnicas alternativas podrían usar
deflexiones existentes para predecir las deflexiones requeridas en sitios
específicos. Tal procedimiento no es tan simple puesto que las deflexiones de la
vertical son muy dependientes del terreno que rodea el sitio. Schwartz (1979)
describe algunas consideraciones generales sobre este problema para Estados
Unidos.
168

178. 7.2.2 Ecuación Extendida de Laplace
La ecuación extendida de Laplace y las ecuaciones de la deflexión de la vertical
tratadas en la sección 7.2 fueron basadas sobre la base de suposiciones de
paralelismo definidas previamente. Para el análisis de la red existente, y para
mejorar el entendimiento del problema es útil tener ecuaciones de deflexión de la
vertical (incluyendo la ecuación de acimut de Laplace) que no consideran esas
suposiciones.
Esta generalización ha sido tratada por Pick et al. (1973, pág. 430), Grafarend y
Richter (1977), Vincenty (1982) y otros.
Dejemos que ωx , ωy , ωz sean pequeños ángulos de rotación que describen la falta
de orientación angular del sistema geodésico con respecto al sistema astronómico.
Los ángulos de rotación son positivos en la dirección de los punteros del reloj
cuando son vistos desde el origen de los ejes. Bajo estas circunstancias la relación
entre los acimuts astronómico y geodésico puede ser escrita como (Vincenty,
1983, 01.20, comunicación privada),
α = A − sin αcot z (Φ − ϕ) − (sin ϕ − cos ϕ cos αcot z )( Λ − λ) + a1ωx + a2 ωy + a3 ωz
(7.35)
Las expresiones para a1 , a 2 , a3 dependen de la interpretación de la falta de
orientación. Los coeficientes dados en la Tabla 1 de Grafarend y Richter (1977)
suponen una rotación del sistema de referencia astronómico. Otra interpretación
considera un cambio en el sistema astronómico y un cambio resultante en las
coordenadas geodésicas. Claramente podemos también considerar cambios en las
deflexiones astrogeodésicas de la vertical debido a los cambios de los sistemas de
coordenadas. Por ejemplo, los cambios en el acimut astronómico ( dA ), latitud
astronómica ( dΦ ), y longitud astronómica ( dΛ ) causados al ir de un sistema
antiguo a un nuevo sistema podrían ser (Vincenty, 1982, pág. 240):
( )
dA = cos λωx + sin λωy / cos ϕ
dΦ = − sin λωx + cos λωy (7.36)
( )
dΛ = tan ϕ cos λωx + sin λωy − ωz
169

179. Si suponemos ningún cambio en el sistema geodésico, los correspondientes
cambios en las deflexiones de la vertical, podrían ser:
dξ = dΦ
(7.37)
dη = dΛ cos ϕ
Una revisión más completa de este problema es dada por Vincenty (1983) y
Vanicek y Carrera (1983).
7.3 Ondulación Astrogeodésica del Geoide
En forma resumida se observó en la sección 1 el concepto de geoide como una
superficie irregular correspondiente al Nivel Medio del Mar (NMM) en las áreas
oceánicas y su extensión en áreas continentales. La localización del geoide con
respecto a un elipsoide puede ser especificada a través de las ondulaciones del
geoide. También podemos localizar el geoide con respecto a un elipsoide
específico de un datum geodésico dado usando deflexiones astrogeodésicas de la
vertical.
En la Figura 7.4 se esquematiza el geoide con respecto al elipsoide de un datum
geodésico.
P es el punto en el Elipsoide
P’ es el punto en el Geoide
Centro del Elipsoide P’
Asociado con el • Superficie Geoidal
P• NAG
Datum Geodésico
Elipsoide de Referencia
Figura 7.4 Ubicación del Geoide con Respecto al Elipsoide de Referencia de un
Datum Específico
En esta figura P es un punto en el elipsoide y P’ es el punto correspondiente en el
geoide. La separación en una dirección vertical entre P y P’ es la ondulación
170

180. astrogeodésica, NAG. La cantidad es positiva cuando el geoide está fuera del
elipsoide.
Para calcular las ondulaciones astrogeodésicas consideramos un perfil geoide-
elipsoide en una dirección definida por el acimut α, según se muestra en la Figura
7.5.
ε
Normal al Normal al
ε
B
A ds d
Geoid
Elipsoid
Figura 7.5 Perfil Geoidal Astrogeodésico con Acimut α
El ángulo en A entre la normal elipsoidal y la normal de gravedad es la deflexión
total de la vertical, ε, en la dirección de la sección escogida. Sea B un punto en el
geoide, ubicado a una distancia diferencial, ds, de A. El cambio en la ondulación
geoidal alejándose desde A a B es dN. De la Figura 7.5 podemos escribir:
dN
ε=− (7.38)
ds
Donde el signo menos es una convención introducida para mantener la
consistencia de las definiciones previas de las deflexiones astrogeodésicas.
Escribimos (7.38) como:
dN = −ε ⋅ ds (7.39)
donde (desde (7.32))
ε = ξcos α + ηsin α (7.40)
171

181. Ahora considere la integración de (7.39) desde el punto A hasta un punto ( en
D)
una red. Tenemos desde (7.39) y (7.40):
D D
N D − N A = ∫ dN = − ∫ (ξcos α + ηsin α)ds (7.41)
A A
Para evaluar (7.41) necesitamos ξ y η a lo largo de la ruta que conecta los puntos
A y D. Notamos que (7.41) nos permite calcular solamente las diferencias de
ondulación astro-geodésica. Para una ondulación “absoluta” es necesario que la
ondulación sea definida en un punto de la red geodésica. En un número de casos
es conveniente definir la ondulación astrogeodésica como cero en el punto origen
del datum geodésico.
La implementación actual de (7.41) es efectuada por integración numérica usando
estaciones vecinas. Si consideramos dos estaciones i y j separadas por una
distancia sij, con componentes de l deflexión en cada estación, podemos escribir
a
(7.41) como:
N ij = −
s ij
2
((ξ + ξ )cos α + (η + η )sin α )
i j ij i j ij (7.42)
Con el objeto de calcular las ondulaciones astrogeodésicas en un área se pueden
estimar y ajustar perfiles astrogeodésicos para formar un juego consistente de
ondulaciones astro-geodésicas. Por ejemplo, considere la grilla mostrada en
Figura 7.6
D C
L1
A B
Figura 7.6 Grilla Astrogeodésica
172

182. En cada punto de la grilla podríamos tener deflexiones astrogeodésicas que son
usadas para calcular las diferencias de ondulación. En un circuito tal como L1 la
suma de las ondulaciones astrogeodésicas debe ser cero.
∑N ij
=0 (7.43)
L1
Este tipo de condición puede ser usado para formar un juego de ecuaciones de
condición, como es efectuado en el ajuste de redes de nivelación, para una única y
mejor estimación del juego de ondulaciones astrogeodésicas. Tal procedimiento
fue esencialmente usado por Fischer et al (1967) en la producción de cartas
astrogeodésicas de América del Norte y América Central. Carroll y Wessells
(1975) describen un geoide astrogeodésico más reciente para Estados Unidos.
Una versión más suavizada de este geoide, basado en una función polinomial de
grado 15 de latitud y longitud es mostrada en Figura 7.7. Este mapa muestra las
ondulaciones geoidales c respecto al Datum Norteamérico de 1927. Cuando el
on
Datum cambia también lo harán las ondulaciones astrogeodésicas.
En la Figura 7.8 se muestran las ondulaciones astrogeodésicas del geoide dado
con respecto al Sistema Geodésico Mundial de 1972 (WGS72) (Zeppelín, 1974b).
Comparando las Figuras 7.7 y 7.8 claramente se revelan las diferencias que son
asociadas con el uso de datum geodésico diferentes.
La precisión del cálculo es basada en varios factores. Un factor crítico se
relaciona con las suposiciones de paralelismo efectuadas en la derivación de las
ecuaciones de deflexión astrogeodésica. Si, por ejemplo, los meridianos iniciales
de los sistemas astronómicos y geodésicos no son paralelos, ocurrirá un error
constante en (principalmente) η el cual causará errores en las diferencias de
ondulación astrogeodésica calculadas con la ecuación (7.42).
La precisión del cálculo de ∆N dependerá del espaciamiento de las estaciones
astronómicas a lo largo del perfil. Un espaciamiento típico puede estar en el orden
de 20 km. Sin embargo, en regiones montañosas este espaciamiento podría ser
reducido a 10 o 15 km. para alcanzar una precisión comparable con las de áreas
más planas. Basado en el análisis de cierre de circuitos Bomford (1980), pág.
366) publicó las siguientes estimaciones de precisión en la determinación de ∆N,
basado solamente en los errores de interpolación:
173

183. Área Precisión (Desviación
Estándar) de ∆N
Alpes ± 0,012 lL m
India
± 0,00052 lL m
Finlandia
± 0,00036 lL m
Donde l es el intervalo promedio, en km, entre estaciones astronómicas, y L es
el largo total del perfil.
Otra fuente de error incluye aquel asociado con la longitud astronómica y con la
posición geodésica y su determinación. Robbins (1977) publicó los errores totales
de ∆N siguientes para áreas no montañosas, donde las deflexiones son
determinadas para ± 0,7” y el espaciamiento típico es 25 km.
m ( ∆N ) Tipo de Línea
± 1,5 L / 1000 m Norte – Sur
Este - Oeste
± 1,9 L / 1000 m
Para líneas cortas se puede esperar una mejor precisión. Wenzel (1978), por
ejemplo, da as siguientes estimaciones de precisión de N, basado en un análisis
l
en el área del Mar del Norte.
m( ∆N ) = ±0,03 L m (7.44)
donde el espaciamiento de la estación típica fue 10 km.
Finalmente observamos que las cantidades astronómicas usadas para el cálculo
de la deflexión de la vertical deben ser cantidades reducidas al geoide desde el
punto de observación actual; y las posiciones geodésicas deben ser aquellas
referidas al elipsoide basado en la reducción de todos los datos medidos para el
elipsoide. Si este último procedimiento no es seguido deben efectuarse
correcciones adicionales, como las describe Fischer (1967).
174

184. 7.4 Reducción de Distancias Medidas al Elipsoide
Las distancias que son medidas en una red geodésica son usualmente reducidas, a
lo menos en principio, al elipsoide sobre el cual los cálculos son efectuados. Tal
reducción es análoga a la corrección de dirección de las deflexiones de la vertical
tratadas en la sección 7.2.1.
En esta sección consideraremos dos casos de reducción. El primer caso se refiere
al de la reducción de líneas base que han sido medidas con respecto a la vertical
local. El segundo caso considera la reducción de distancia de cuerda medidas con
equipos electrónicos de medición de distancia, lo cual es independiente de la
dirección de la gravedad.
Para considerar el primer caso seguiremos Heiskanen y Moritz (1967, pág. 190).
En la Figura 7.9 hemos medido una distancia dl sobre la superficie de la Tierra.
La inclinación de la línea con respecto a la horizontal local es β, y la deflexión de
la vertical en la dirección (α) de la línea es ε dado por (7.40). El elemento de
línea diferencial paralelo al elipsoide es ds mientras que el elemento
correspondiente en el elipsoide es ds0 . Aproximamos el elipsoide a una esfera
cuyo radio es el radio en la dirección α dado por la ecuación (3.104).
d B
ds
β
A ε d ’
Horizonte Local
HA
hA
Geoide
NA ds0
Elipsoide
R
Figura 7.9 Reducción de la Línea Base (después de Heiskanen y Moritz, 1967)
175

185. El valor de ds es dl proyectado sobre una línea paralela al elipsoide:
ds = dl cos (β − ε) = dl cos β + ε ⋅ dl sin β (7.45)
haciendo
dl ' = dl cos β
dl sin β ≈ dh
Podemos escribir (7.45) en la forma:
ds = dl'+ε ⋅ dh (7.46)
d l' es la proyección dl sobre la horizontal local. Ahora necesitamos reducir ds
a ds 0 lo cual puede ser realizado mediante simple proporcionalidad.
ds R + h h
= =1+ (7.47)
ds0 R R
donde h = H + N , y donde H es la altura ortométrica (altura sobre el NMM) y N
es la ondulación geoidal para un elipsoide específico. Sustituyendo (7.46) en
(7.47) y manteniendo un término en la expansión de (1 + h / R) tenemos:
h h
ds 0 = ds − ds 0 = dl'+ε ⋅ dh − ds0
R R
o dejando que
ds 0
dψ = (7.48)
R
tenemos
176

186. ds 0 = dl'+ε ⋅ dh − h ⋅ dψ = dl'+d (ε ⋅ h) − h ⋅ d (ψ + ε ) (7.49)
Ahora consideremos una línea que va desde A hasta B. Integramos (7.49) entre
los dos puntos para encontrar:
B
ds 0 = l'+εB hB − εA h A − ∫ hd (ψ + ε) (7.50)
A
Si la altura sobre el elipsoide es tomada como constante hm entre A y B, usando
(7.48), podemos escribir (7.50) como:
s0 = l '+εB hB − ε A h A − hm (εB − ε A ) −
hm
s (7.51)
R 0
donde hm es la elevación media a lo largo de la línea. En (7.50) y (7.51) l ' es:
B
l' = ∫ dl cos β (7.52)
A
Lo cual es la suma de las componentes horizontales de las distancias medidas.
La ecuación (7.51) es la ecuación básica para la reducción de las líneas base
medidas. Observamos que la aplicación de esta fórmula requiere información
sobre la deflexión de la vertical y la ondulación geoidal para lograr reducciones
apropiadas de las distancias. En algunas aplicaciones los efectos de las
deflexiones han sido desapropiadamente omitidos. Los efectos de tales omisiones
pueden ser críticos si las diferencias del punto final de elevación son grandes y/o
las deflexiones son significativamente diferentes en el punto final de las líneas.
La geometría del segundo caso de reducción es mostrada en la Figura 7.10
177

187. B
A hB
hA Geoide
s0 Elipsoide
A0 B0
R
ψ
0
Figura 7.10 Reducción de Distancias de Cuerda al Elipsoide
En esta figura el valor de h es la suma de las alturas ortométricas más la
ondulación astro-geodésica. El radio de la esfera, R, es (RA(α) + RB(α))/2. En esta
deducción, nuevamente seguimos a Heiskanen y Moritz (1967, pág. 192) y
aproximamos el elipsoide a una esfera de radio R en el acimut determinado por
(3.104).
Usando la ley de cosenos en el triángulo 0AB tenemos:
l 2 = (R + hA ) 2 + ( R + hB ) 2 − 2( R + h A )( R + hB ) cos ψ (7.53)
Si usamos la identidad
ψ
cos ψ = 1 − 2 sin 2 (5.54)
2
podemos escribir (7.53) en la forma:
 h  h  ψ
l 2 = (hB − h A ) 2 + 4 R 2 1 + A  1 + B  sin 2 (7.55)
 R  R 2
Ahora la distancia de cuerda correspondiente entre los puntos reducidos al
elipsoide sería:
178

188. ψ
l 0 = 2R sin (7.56)
2
que puede usarse en (7.55) para escribir (con ∆h = hB − hA ):
 h  h 
l 2 = ∆h 2 + 1 + A  1 + B  l 0 2 (7.57)
 R  R
Resolviendo para l 0 tenemos:
l 2 − ∆h 2
l0 = (7.58)
 hA   hB 
1 +  1 + 
 R  R
Ahora podemos usar las ecuaciones tales como (4.57) o (4.58) para reducir la
distancia de cuerda a la distancia, s0 , en el elipsoide.
La exactitud de la ecuación (7.58) ha sido estudiada por Thomson y Vanicek
(1974) hallándola adecuada para todo propósito práctico. Vincenty (1975)
también consideró la reducción de distancias espaciales al elipsoide, incorporando
deflexiones de la vertical con el fin de obtener diferencias de ondulaciones
astrogeodésicas.
179

189. 8 FÓRMULAS DIFERENCIALES DEL PRIMER Y SEGUNDO TIPO
Para aplicaciones tales como la formación de ecuaciones de observación para ajuste de
triangulación y trilateración, y para la formación de ecuaciones útiles en la determinación del
tamaño y forma de la Tierra, es necesario obtener ecuaciones que relacionen cambios
diferenciales en varias cantidades. Tales ecuaciones son divididas en dos tipos.
Fórmulas diferenciales del primer tipo son aquellas que producen cambios en las direcciones y
coordenadas geodésicas como función de las coordenadas iniciales y acimut de la línea.
Fórmulas diferenciales del segundo tipo son aquellas que producen correcciones para las
coordenadas y direcciones resultantes de cambios en el radio ecuatorial y el parámetro que
está definiendo la forma, tal como el achatamiento.
La revisión de estas fórmulas diferenciales puede ser encontrada en Bagratuni (1967, pág.
280), Jordan (Vol. III, segunda mitad, pág. 439), Zakatov (1962, pág. 104), Grushinskiy
(1969, pág. 84), y Tobey (1927).
8.1 Fórmulas Diferenciales del Primer Tipo
Supongamos que hemos calculado las coordenadas ϕ2 , λ2 y el retro-acimut α21 de un punto
P2 basado en las coordenadas ϕ1 , λ1 del primer punto P1, y una distancia s y acimut α12 .
Ahora deseamos encontrar el cambio en ϕ2 , λ2 y α21 si cambiamosϕ1 , λ1 , α12 y s.
Podríamos expresar esto analíticamente escribiendo lo siguiente:
∂ϕ2 ∂ϕ ∂ϕ2
dϕ2 = dϕ1 + 2 ds + dα12 (8.1)
∂ϕ1 ∂s ∂α12
∂λ2 ∂λ ∂λ2
dλ2 = dϕ1 + 2 ds + dα + dλ1 (8.2)
∂ϕ1 ∂s ∂α12 12
∂α21 ∂α21 ∂α
dα21 = dϕ1 + ds + 21 dα12 (8.3)
∂ϕ1 ∂s ∂α12
Observamos que en la ecuación (8.1) y (8.3) no aparece un término de longitud. Esto es por la
simetría rotacional del elipsoide de referencia. Por conveniencia, las ecuaciones (8.1), (8.2) y
(8.3) son escritas en la forma siguiente:
180

190. dϕ2 = dϕ2 ϕ 1 + dϕ2 s + dϕ2 α12 (8.4)
dλ2 = dλ1 + dλ2 ϕ1 + dλ2 s + dλ2 α12 (8.5)
dα21 = dα21ϕ1 + dα21 s + dα21α21 (8.6)
La derivación de estas ecuaciones es simple para algunos casos y compleja para otros. Los
autores mencionados previamente han obtenido cada uno diferentes soluciones para este
problema. Bagranuti y Jordan han dado las expresiones más rigurosas. Zakatov y Grushinskiy
dieron resultados similares, pero ciertos términos en un modo levemente diferente.
Ahora derivamos algunos términos dados en las ecuaciones (8.4, 5, y 6). Primero
consideramos el efecto de extender una geodésica de longitud s por una longitud diferencial ds.
El efecto de esta extensión en el movimiento desde el punto F a F 2 es mostrado en la Figura
8.1.
s
dλ2
G
F F2
α12 α21 ds
s
dϕ2
Figura 8.1 Efecto Diferencial de una Extensión Longitudinal
G es un punto en el meridiano a través de F y en el paralelo a través de F2. Tenemos:
FG = ds cos(α21 − 180)
(8.7)
FG = −ds cos α21
También tenemos:
181

191. FG = M 2 dϕ2 S (8.8)
Igualando las ecuaciones (8.7) y (8.4) queda:
− cos α21 ⋅ ds
dϕ2 s = (8.9)
M2
Luego calculamos GF2 como:
GF2 = ds sin (α21 − 180) = − sin α21 ⋅ ds (8.10)
También tenemos GF2 como:
GF2 = N 2 cos ϕ2 ⋅ dλ2 s (8.11)
Igualando las ecuaciones (8.10) y (8.11) queda:
− sin α21 ⋅ ds
dλ2 S = (8.12)
N 2 cos ϕ2
Para obtener el cambio en el retro-acimut aplicamos la ecuación de Clairaut (4.81) para una
geodésica escrita en la forma siguiente:
N 2 cos ϕ2 sin (α21 − 180) = c,
ó una constante (8.13)
N 2 cos ϕ2 sin α21 = −c = c '
Diferenciamos esta expresión suponiendo que todas las cantidades son variables. Por tanto:
N 2 cos ϕ2 cos α21 dα21 + d ( N 2 cos ϕ2 ) sin α21 = 0 (8.14)
Desarrollando la diferenciación de N 2 cosϕ2 encontramos:
d ( N 2 cos ϕ2 ) = −M sin ϕ2 d ϕ2 (8.15)
Con esta última expresión sustituida en la ecuación (8.14) y efectuada la solución para dα21
conseguimos:
M2
dα21 = tan α21 tan ϕ2 dϕ2 (8.16)
N2
182

192. Hasta este punto la ecuación (8.16) es una ecuación general en el sentido de que un cambio de
dϕ2 produce un cambio dα21 . Si estamos interesados en el efecto ds sobre dα21 , sustituimos
la ecuación (8.9) en (8.16) para obtener:
− sin α21 tan ϕ2
dα21 s = ds (8.17)
N2
Seguidamente consideramos los efectos variados cuando el acimut en el primer punto es
cambiado una cantidad dα12 . Esta situación es mostrada en la Figura 8.2 donde el punto F es
el punto final original de la línea y F2 es el punto final después de la rotación.
P
F G
α12
A F2
dα12
Figura 8.2 Efecto Diferencial de un Cambio de Acimut
En la Figura 8.2 hemos dibujado el arco FG de tal modo que este es perpendicular al
meridiano que pasa por F2. Adicionalmente, debido a la rotación, el ángulo FF2A se acercará a
un ángulo recto, así el ángulo GF2F será 270-α21. Entonces vemos desde la figura que:
GF2 = FF2 cos(GF2 F ) = FF2 cos (270 − α21 ) = −FF2 sin α21 (8.18)
De lo visto en la Sección 4.22 tenemos:
FF2 = w ⋅ dα12 (8.19)
lo cual puede ser sustituido en (8.18) para escribir:
GF2 = −w sin α21 dα12 (8.20)
El lado GF2 podría también ser expresado como:
− M 2 dϕ2 α12 (8.21)
183

193. Donde el signo menos proviene del hecho que un incremento de α12 causará una reducción en
la latitud.
Igualando las ecuaciones (8.21) y (8.20) y resolviendo para dϕ2α12 encontramos:
sin α21
dϕ2 α12 = w dα12 (8.22)
M2
Para encontrar el cambio en longitud debido a esta rotación, expresamos FG como sigue:
FG = FF2 sin (FF2 G) = FF2 sin (270 − α21 ) = −FF2 cos α21 (8.23)
Usando la ecuación (8.19) para FF2, y notando que:
FG = N2 cos ϕ2 dλ2 α12 (8.24)
podemos despejar dλ2 α12 de modo que:
− w cos α21
dλ2α12 = dα12 (8.25)
N 2 cos ϕ2
Ahora nos abocamos a la derivación del cambio del retro-acimut α21 causado por dα12 . Para
realizarlo consideramos la Figura 8.3:
F1
wdα12
F2
F3 ds
α12 s
A
dα12 Meridiano a
través de F1
Figura 8.3 Cambio del Retro-Acimut Debido a dα12
En esta figura:
184

194. F1 = punto final original de la línea.
F2 = nuevo punto final después de la rotación dα12 .
F3 = punto en AF2 sobre el meridiano a través de F1.
Ahora dejemos que dα21 = dα2 donde dα2 es el acimut hacia delante en el punto 2 (esto es
F1). Por ahora designamos el cambio total en dα2 como d α2 r . Consideraremos esto como la
composición de dos cambios (dα2 m y d α2 e ). Como F1 se aproxima a F2, permitamos que
dα2 m sea el cambio en α21 . Ahora también consideremos un cambio especial en dα2 cuando
F2 es desplazado ds = F2F3 hasta F3. Definimos esto como d α2 e . Podemos notar que el valor
de d α2 r es simplemente la suma de las correcciones:
dα2 r = dα2 m + dα2 e (8.26)
Para encontrar dα2 m notamos que es simplemente el cambio en retro-acimut según nos
movamos a lo largo de un meridiano.
F B
wdα12
E dα2m
A
D C
Figura 8.4 Detalle de los Efectos del Cambio de Retro-Acimut
Tenemos:
B = punto final original.
C = punto final después de la rotación dα12 .
D = punto en el meridiano a través de B, en la línea AC.
F = punto en la línea original determinado por una línea paralela a BC.
E = punto en una línea paralela a FB a través de D.
Ahora DC representa un cambio de distancia causado por la rotación. Si dα12 es positivo ds
es negativo. Para facilidad, trabajaremos con acimut hacia delante. En B el acimut hacia delante
es FBD, mientras que en D este es CDB. La diferencia es el cambio requerido.
185

195. dα2 m = CDB − FBD = EDC
tenemos:
CE
dα2 m = donde CE = BC – DF y DC = -ds
DC
entonces:
BC − DF
dα2 m =
− ds
Usando las definiciones de w, tenemos:
BC = wdα12
Si observamos que yendo desde B a F w será ahora w+dw (dw será negativo), podemos
expresar:
DF = (w + dw)dα12
así:
wdα12 − ( w + dw)dα12
dα2 m = (8.27)
− ds
La ecuación (8.27) es válida para puntos que se mueven a lo largo de un meridiano. En nuestro
particular caso, (8.27) es requerido en (8.26) como dα2 m . Ahora necesitamos d α2 e el cual es
simplemente la ecuación (8.17):
− ds tan ϕ2 sin α21
dα2 e = (8.28)
N2
In este caso ds = F2F3 y es expresado como:
ds = wdα12 cot α21 (8.29)
Combinando las ecuaciones (8.29), (8.28), (8.27) con (8.26) podemos escribir:
186

196.  dw w tan ϕ2 cos α21 
dα2 = 
 ds − dα12
 (8.30)
 N2 
Recordaremos que esta ecuación permite el cambio en el retro-acimut en el segundo punto
causado por el cambio de acimut en el primer punto considerando que dα2 = dα21 . El valor
de dw / ds podría ser encontrado diferenciando la ecuación (4.103). Esto podría permitir una
serie de expresiones por lo cual es conveniente formular otra aproximación. Recordemos que:
N 2 cos ϕ2 sin α2 = N 1 cos ϕ1 sin α12 = − N 2 cos ϕ2 sin α21 (8.31)
Diferenciamos esto usando los resultados dados en (8.15), reconociendo que ϕ1 es una
constante. Así:
− N 2 cos ϕ2 cos α21 dα2 + M 2 sin ϕ2 sin α21 dϕ2 = N1 cos ϕ1 cos α12 dα12 (8.32)
Ahora usamos el valor de dϕ2 de (8.22) en la ecuación de arriba para encontrar:
 − N1 cos ϕ1 cos α12 w tan ϕ2 tan α21 sin α21 
dα2 =  +  dα12 (8.32a)
 N 2 cos ϕ2 cos α21 N2 
Considerando que las expresiones (8.30) y (8.32a) son lo mismo podemos despejar dw/ds y
encontrar:
dw  − N 1 cos ϕ1 cos α12 w tan ϕ2 
= +  (8.33)
ds  N 2 cos ϕ2 cos α21 N 2 cos α21 
La derivación descrita en las últimas páginas representa solamente una porción de las
derivaciones requeridas por las ecuaciones (8.4, 5, 6). Detendremos la continuación de estas
derivaciones para resumir los cambios que hemos derivado y entregar otros, sin derivación,
aunque estas podrían ser encontradas en la literatura. Tenemos:
ϕ1 M1   dw 
dϕ2 =− sin α12 sin α21  ds  + cos α12 cos α21  dϕ1 , (Jordan, pág. 441)
M2   2 
− cos α21
dϕ2 s = ds ; (nuestra ecuación (8.9))
M2
sin α21
dϕ2 α12 = w dα12 ; (nuestra ecuación (8.22))
M2
187

197. ϕ1 M1   dw 
dλ2 = sin α12 cos α2  ds  − cos α12 sin α2  dϕ1 , (Jordan, pág. 442)
N 2 cos ϕ2   2 
− sin α21 ⋅ ds
dλ2 S = ; (nuestra ecuación (8.12))
N 2 cos ϕ2
− w cos α21
dλ2α12 = dα12 ; (nuestra ecuación (8.25))
N 2 cos ϕ2
M M M  dw  dw  M  dw 
dα ϕ1 =  1 sinα − 1 sin α cosα tanϕ − 1     sin α + 1   sinα cosα tanϕ dϕ
w  ds 1 ds 2 N2  ds 2
21 12 2 12 2 1 1 2 2 1
w N2 
(Jordan, pág. 442)
− sin α21 tan ϕ2
dα21 s = ds ; (nuestra ecuación (8.17))
N2
α 12  − N1 cos ϕ1 cos α12 w tan ϕ2 tan α21 sin α21 
dα21 = +  dα12 ; (nuestra ecuación (8.32))
 N 2 cos ϕ2 cos α21 N2 
ó
α 12  dw w tan ϕ2 cos α21 
dα21 =
 ds −  dα12 ; (nuestra ecuación (8.30))

 N2 
El resumen de ecuaciones precedentes será referido como la ecuación ...... (8.34)
8.2 Fórmulas Diferenciales del Segundo Tipo
Con el objeto de determinar la influencia del cambio de los parámetros del elipsoide sobre el
cálculo de las coordenadas y direcciones podemos diferenciar cualquiera de las ecuaciones
derivadas para el problema directo, tales como (6.19) (las series de Legendre) o las
ecuaciones de Puissant, tales como las dadas en la ecuación (6.40). Por conveniencia
escogemos usar las ecuaciones (6.19) manteniendo los primeros términos solamente y dejando
que las evaluaciones tengan lugar en una latitud media. Entonces escribimos:
3 2 2
(
(ϕ2 − ϕ1 ) = V cos α s = cos α12 s = s cos α12 1 − e sin ϕm )3/ 2
c m
Mm a 1 − e2 ( ) (8.35)
188

198. (λ2 − λ1 ) = V sin α
s=
sin α12
s=
s sin α12 1 − e 2 sin 2 ϕm ( )
1/2
(8.36)
c cos ϕ m N m cos ϕm a cos ϕm
s sin α12 tan ϕm
(α21 − α12 ) − 180o =
V
sin α tan ϕ s = = (λ2 − λ1 ) sin ϕm (8.37)
c m Nm
Primero diferenciamos la ecuación (8.35) con respecto a a y e2. Luego queda:

d(ϕ2 −ϕ1 ) = s cosα  2
(
−1 1−e 2 sin 2 ϕ ) 3/ 2
1 3 2
da+ − sin ϕm
(
1− e2 sin2 ϕm )
1/ 2
+
(1− e
2
sin2 ϕm ) 3/ 2
 2
de 
( ) ( )
m
12
a
 1− e 2
a 2
 1− e2 (1−e )
2 2
 
 
(8.38)
La cual puede ser escrita en la forma:
d (ϕ2 − ϕ1 ) =
(
s cosα12 1 − e 2 sin 2 ϕm )
3/2
 − da  3 2
+  − sin ϕm
1
+
1  2
 de 
(
a 1− e2 ) 
 a
  2 1 − e 2 sin 2 ϕm 1 − e 2   
(8.39)
Notamos que el primer término a la derecha de (8.39) es simplemente (ϕ2 − ϕ1 ) según es
dado por la ecuación (8.35). Para transformar (8.39) en una forma simple recordamos que
e 2 = 2 f − f 2 , luego:
de 2 = 2(1 − f )df ≈ 2df (8.40)
Sustituyendo la aproximación de (8.40) en (8.39), y usando la ecuación (8.35) queda:
 da  2 3 sin 2 ϕm  
d (ϕ2 − ϕ1 ) = −(ϕ2 − ϕ1 ) −  −
( )  df  (8.41)
 a 1 − e 1 − e 2 sin 2 ϕm
2
 
( ) ( )
Dejando que 1 − e 2 y 1 − e 2 sin 2 ϕm se igualen a uno, en la ecuación (8.41), finalmente
obtenemos:
 da
( 
d (ϕ2 − ϕ1 ) = −(ϕ2 − ϕ1 )  − 2 − 3 sin 2 ϕm df  ) (8.42)
a 
Ahora diferenciamos la ecuación (8.36) con respecto a a y e2. Tenemos al inicio:
189

199. d (λ2 − λ1 ) =
s sin α12

(
 − 1 − e 2 sin 2 ϕm )
1/2
da
−
(
sin 2 ϕm 1 − e 2 sin 2 ϕm ) −1 / 2

de 2 
cos ϕm  a2 2a 
 
(8.43)
Simplificando queda:
d (λ2 − λ1 ) =
− s sin α12
a cos ϕm
(
1 − e 2 sin 2 ϕm )
1/ 2  da
 +
sin 2 ϕm
(

de 2 
) (8.44)
 a 2 1 − e sin ϕm
2 2

Notamos que el primer término del lado derecho de la ecuación (8.44) es lo mismo que la
(
ecuación (8.36), dejando que de 2 = edf , y adoptando el término 1 − e 2 sin 2 ϕm igual a uno, )
la ecuación (8.44) puede ser escrita como:
 da 
d (λ2 − λ1 ) = −(λ2 − λ1 ) + sin 2 ϕm df  (8.45)
 a 
Para encontrar los efectos del retro-acimut, primero diferenciamos la ecuación (8.37) en la
forma siguiente:
dα21 = d (λ2 − λ1 ) sin ϕm (8.46)
Entonces, usando la ecuación (8.45) por d (λ2 − λ1 ) tenemos:
 da 
dα21 = −( λ2 − λ1 ) sin ϕm  + sin 2 ϕm df  (8.47)
 a 
Notamos que el primer término del lado derecho de la ecuación (8.47) es el cambio total del
acimut, dα , en el movimiento desde el punto uno hasta punto dos.
La derivación de arriba ha sido efectuada con varias aproximaciones. Consecuentemente las
ecuaciones son solamente válidas para líneas de hasta 40-50 km para una precisión de 0,001”-
0,002”. Con el objeto de derivar expresiones más exactas es conveniente diferenciar las
fórmulas de series de potencias extendidas tales como aquellas dadas en la ecuación (6.19).
Los resultados de tales derivaciones son dados por Bragranuti (1967, pág. 286):
190

200.  V 2 cos 2 ϕm tan ϕm 
d (ϕ2 − ϕ1 ) = − (ϕ2 − ϕ1 ) − tan ϕmη2 (ϕ2 − ϕ1 )2 − (λ2 − λ1 ) da
3
 2 2  a
 3(ϕ2 − ϕ1 ) cos ϕm tan ϕm
 ( )
2 2
+ [ (ϕ2 − ϕ1 ) cos ϕm  2 − t + η + η tan ϕm  −
7 2
2 − 2η2 + 2t 2η2
2 2 2 2
 2  2
+
(λ2 − λ1 )2 cos 4 ϕm tan ϕm  tan 2 ϕ 1 1 
+ η2 tan 2 ϕm + η2 tan 4 ϕm  ]df
 m
2  2 2 
(8.48)
[ (
d (λ2 − λ1 ) = − (λ2 − λ1 ) + (λ2 − λ1 )(ϕ2 − ϕ1 ) tan ϕm 1 − η2 )] da
a
− [ (λ2 − λ1 ) cos 2 ϕm  tan 2 ϕm − η2 tan 2 ϕm + η2 tan 4 ϕm  + (λ2 − λ1 )(ϕ2 − ϕ1 )
1 1
 
 2 2 
 3 1 
⋅ cos 2 ϕm tan ϕm  tan 2 ϕm − η2 tan 2 ϕm + η2 tan 4 ϕm ]df
 2 2 
(8.49)
[ (
dα21 = − (λ2 − λ1 )cos ϕm tan ϕm + (λ2 − λ1 )(ϕ2 − ϕ1 ) cos ϕm 1 + tan 2 ϕm − η2 tan 2 ϕm )] da
a
− [ (λ2 − λ1 ) cos 3 ϕm tan ϕm  tan 2 ϕm − η2 tan ϕm + η2 tan 4 ϕm 
1 1
 
 2 2 
 
− (λ2 − λ1 )(ϕ2 − ϕ1 ) cos 3 ϕm 1 − tan 2 ϕm − tan 4 ϕm + η2 + 2η2 t 2 ]df
1
 2 
(8.50)
Con esto concluimos la revisión de las fórmulas diferenciales del primer y segundo tipo. En la
sección siguiente veremos como las fórmulas del primer tipo pueden ser usadas para desarrollar
las ecuaciones de observación en triangulación y/o trilateración.
191

201. 9 ECUACIONES DE OBSERVACIÓN PARA TRIANGULACIÓN Y
TRILATERACIÓN CALCULADAS EN EL ELIPSOIDE
Las ecuaciones revisadas en la sección 8 nos permiten desarrollar las ecuaciones de
observación para ser usadas con mediciones de acimut (direcciones) y distancias
efectuadas para el control horizontal convencional. Específicamente, ahora necesitamos
desarrollar ecuaciones que relacionen cambios en el acimut y distancias entre dos puntos
con los cambios correspondientes de las coordenadas geodésicas. Nuestras observaciones
siguen de cerca las efectuadas por Tobey (1928).
9.1 Relaciones Entre Distancias y Direcciones
Primero considere el cambio en latitud de un segundo punto, causado por un cambio de
distancia ( y un cambio de acimut (dα12 ) en el primer punto. De las ecuaciones (8.9) y
ds)
(8.22) podemos escribir el efecto total de estos dos cambios como sigue:
w sin α12 cos α21
dϕ2 = dα12 − ds (9.1)
M2 M2
El efecto correspondiente en longitud es:
− w cos α21 sin α21
dλ2 = dα12 − ds (9.2)
N 2 cos ϕ2 N 2 cos ϕ2
Usando la ecuación (8.17) y (8.30) el cambio total en α21 será:
 dw w tan ϕ2 cos α21  tan ϕ2 sin α21
dα21 =  −  dα12 − ds (9.3)
 ds N2  N2
Ahora deseamos resolver la ecuación (9.1), (9.2) y (9.3) para ds, dα12 y dα21 en términos
de dϕ2 y dλ2 . Para hacerlo, primero multiplicamos (9.1) por cos α21 / N 2 cos ϕ2 y la
ecuación (9.2) por sin α21 / M 2 . Entonces sumamos las ecuaciones resultantes para
obtener:
ds = − M 2 cos α21dϕ2 − N 2 cos ϕ2 sin α21 dλ2 (9.4)
Seguidamente, multiplicamos la ecuación (9.1) por sin α21 / N 2 cos ϕ2 y la ecuación (9.2)
por − cos α21 / M 2 . Entonces sumamos las ecuaciones resultantes para obtener:
192

202. wdα12 = M 2 sin α21 dϕ2 − N 2 cos ϕ2 cos α21 dλ2 (9.5)
Si sustituimos el valor de ds y dα12 de (9.4) y (9.5) dentro de (9.3) encontramos:
dw
wdα21 = M 2 sin α21 dϕ2 + N1 cos ϕ1 cos α12 dλ2 (9.6)
ds
Teniendo estas tres ecuaciones para el caso donde un punto es libre de moverse,
podríamos desarrollar fórmulas para el caso cuando ambos puntos extremos son libres de
moverse. Para hacerlo, consideramos los puntos extremos finales originales en P1 y P2
desplazados una pequeña cantidad hasta T1 y T2 según es mostrado en la Figura 9.1.
T T
α1
P P
α2
Figura 9.1 Movimientos Diferenciales de los Puntos Extremos de la Línea
Primero consideramos P2 desplazado hasta T , resultando cambios en distancias y acimut
2
de las líneas designados como: ds a , dα12 a , dα21a . Tales cambios podrían ser dados
directamente por las ecuaciones (9.4), (9.5) y (9.6). También desplazamos P1 hasta T2
causando cambios adicionales ds b , dα12 b , dα21b . Ignorando los efectos de mayor orden, el
desplazamiento total debería ser la suma de esos dos juegos de desplazamientos. Por ello
dejamos:
ds t = ds a + ds b
dα12 t = d α12 a + dα12b (9.7)
dα21t = dα21a + dα21b
Ahora el valor de dsa está dado en la ecuación (9.4). Usando (9.4) el valor de dsb es:
ds b = −M 1 cos α12 dϕ1 − N1 cos ϕ1 sin α12 dλ1
193

203. Entonces:
ds t = −M 2 cos α12 dϕ2 − N 2 cos ϕ2 sin α21dλ2 − M 1 cos α12 dϕ1 − N1 cos ϕ1 sin α12 dλ1
(9.8)
No obstante, tenemos por el teorema de Clairaut:
N1 cos ϕ1 sin α12 = − N 2 cos ϕ2 sin α21
luego (9.8) se transforma en:
ds t = −M 2 cos α12 dϕ2 − M 1 cos α12 dϕ1 − N 2 cos ϕ2 sin α21 ( dλ2 − dλ1 ) (9.9)
La ecuación (9.9) nos permite determinar la ecuación de observación de distancia
requerida donde las distancias son consideradas como reducidas al elipsoide.
Podríamos calcular el cambio de acimut en el primer punto usando la ecuación (9.5) para
dα12a, y la ecuación (9.6) para dα21b, cuando son aplicadas al primer punto. Así:
1 dw 
dα12 b =  M 1 sin α12 dϕ1 + N 2 cos ϕ2 cos α21 dλ1  (9.10)
w ds 
Combinando ésta con (9.5) queda:
1 dw 
dα12 t =  M 2 sin α21 dϕ2 + M 1 sin α12 dϕ1 − N 2 cos ϕ2 cos α21 ( dλ2 − dλ1 ) (9.11)
w ds 
Recordemos que el valor de w puede ser encontrado con la ecuación (4.103) mientras que
dw/ds es encontrado con la ecuación (8.33).
La ecuación (9.11) no es una forma simple para el cálculo; intentos de simplificación
podrían ser efectuados para usarla en líneas de extensión reducida. La primera
simplificación es hecha permitiendo que se adopte una esfera por el elipsoide, cuyo radio
es el radio medio gaussiano en el primer punto. Entonces la expresión para w se
transforma en:
s
w = R sin (9.12)
R
de este modo:
194

204. dw s
= cos (9.13)
ds R
Ahora insertamos (9.12) y (9.13) en (9.11) usando M 1 = M 2 = N 2 = R para encontrar:
sin α12 sin α21 cos ϕ2 cos α21
dα12 t = dϕ1 + dϕ2 − (dλ2 − dλ1 ) (9.14)
s s s
tan sin sin
R R R
Si expandimos la tangente y el seno en serie y retenemos solamente el primer término,
tenemos:
R sin α12 R sin α21 R cos ϕ2 cos α21
dα12 t = dϕ1 + dϕ2 − (dλ2 − dλ1 ) (9.15)
s s s
La ecuación (9.15) debería ser una aproximación para corregir la relación diferencial en
la esfera, y una aproximación para la relación diferencial en el elipsoide (esto es la
ecuación (9.11)).
Para desarrollar la fórmula usualmente usada en la práctica, modificamos (9.11)
suponiendo que w = s así dw/ds = 1. Entonces (9.11) se transforma en:
dα12 t ≈
1
(M sin α12 dϕ1 + M 2 sin α21dϕ2 − N 2 cos ϕ2 cos α21 ( dλ2 − dλ1 )) (9.16)
s 1
Es claro que (9.16) es solamente una aproximación a un resultado más preciso
representado por (9.11). Olliver (1977) estudió la precisión de la ecuación (9.9) y (9.16)
comparando cambios definidos rigurosamente para diferentes resultados. Para una línea
de 50 Km de extensión el máximo error en acimut fue 0,008” y el error máximo en
distancia fue 0,002 m, cuando los desplazamientos dados fueron 0,15”.
9.2 Las Ecuaciones de Observación
Ahora usamos las fórmulas de cambio diferencial para desarrollar las ecuaciones de
observación de distancia y acimut. Escribimos una ecuación general de observación en la
forma:
∂F
F( X0 ) + dX = LOBS + v (9.17)
∂X
195

205. Donde F es la función que está relacionando las observaciones, LOBS , y los parámetros,
X, del problema; dX son las correcciones para los valores aproximados X0 , de los
parámetros y v es la observación residual. Desde (9.17) escribimos:
∂F
v = F ( X 0 ) − LOBS + dX (9.18)
∂X
∂F
En la sección (9.1) hemos desarrollado las expresiones para dX . Así para una
∂X
observación de distancia podemos escribir:
v s = s0 − sOBS + ds t (9.19)
Donde dst es dado por la ecuación (9.9). En algunos casos un factor de escala
desconocido (por ejemplo s(k-k 0 )) podría ser agregado a esta expresión cuando se
sospechan inconsistencias de escala en los instrumentos y/o las redes.
Ahora consideramos el caso donde observamos un juego de direcciones a varias
estaciones. Después que ha sido desarrollado un ajuste de estación (Bomford, 1980, pág.
30), y después de las correcciones por divergencia de las normales de las secciones
normales a las geodésicas, y también efectuadas las correcciones por las deflexiones de la
vertical, las direcciones son designadas DI, D1 ...Di donde DI es la dirección a lo largo de
la línea inicial. El acimut geodésico de esta línea inicial es αI el cual podría ser solamente
conocido aproximadamente (αI0) entonces escribimos:
αI = αI 0 + Z (9.20)
Donde Z es conocido como la orientación o la corrección de la estación. Dadas las
coordenadas geodésicas aproximadas de dos puntos relacionados con la línea I inicial, αI0
puede ser calculado exactamente. Los acimut “observados” (αI) para la línea i, en la
estación, podrían ser:
αi = αI + Di − DI = αI 0 + Z + Di + DI (921)
Usando αi como la cantidad observada en (9.18) queda:
vi = αi 0 − (αI 0 + Di − DI ) − Z + dα12 t
Donde αi0 es el acimut aproximado a lo largo de la línea i (calculado desde las
α
coordenadas aproximadas) y d 12t podría ser dado, por ejemplo, por la ecuación (9.16).
En general, cada estación para la cual un acimut aproximado inicial es usado tendrá una
corrección de orientación asociada a éste.
196

206. 9.3 La Ecuación de Observación de Acimut de Laplace
Considere la ecuación de acimut de Laplace tal como es expresada en la ecuación (7.27)
αL = A − (Λ − λ) sin ϕ (9.22)
Solamente como valores aproximados de λ son conocidos αL el cual está sujeto a una
corrección encontrada diferenciando (9.22) notando que A y Λ son cantidades observadas
y que ϕ necesita ser conocido solamente en forma aproximada.
dαL = dλ sin ϕ (9.23)
Entonces consideramos que el acimut geodésico “observado” será como sigue:
αOBS = αL + dαL (9.24)
Luego podemos expresar (9.18) como:
v = α0 − (αL + dαL ) + dα12t (9.25)
Usando (9.16) y (9.23), (9.25) puede ser expresado como:
M1 sin α M sin α21 N cosϕ2 cosα21  N cosϕ2 cosα21 
v = α0 −αL + 12
dϕ1 + 2 dϕ2 − 2 dλ2 + 2 −sin ϕ1  dλ1
s s s  s 
(9.26)
En (9.26) α0 es calculado u sando las coordenadas aproximadas de dos puntos, y αL es
calculado desde (9.22) usando las coordenadas observadas y las aproximadas. En el
ajuste, el peso para la ecuación de observación de Laplace es determinado considerando
la precisión de A y Λ que entran en (9.26).
9.4 Formas de Ecuaciones de Observación Alternas
Las técnicas usadas en las secciones previas son aquellas asociadas generalmente con el
ajuste de redes geodésicas bidimensional clásico. Si una red es definida en tres
dimensiones existe una simplificación considerable en el procedimiento de reducción,
197

207. puesto que los puntos están ahora en el espacio y no se requieren reducciones (ya sea por
direcciones o distancias) al elipsoide. Una revisión de varias técnicas de ajuste
tridimensional han sido dadas por Asquenazí y Grist (1983).
Un procedimiento completo de ajuste tridimensional puede ser complicado por la
necesidad de información astronómica y de alturas. Sin embargo, las ecuaciones de
observación desarrolladas para un ajuste tridimensional pueden ser usadas para derivar
nuevas ecuaciones de observación donde las cantidades astronómicas son consideradas
conocidas y los datos de altura son considerados conocidos o se mantienen fijos.
Bowring (1980) y Vincenty (1980b) observan varios aspectos de los nuevos procesos de
ajuste lo cual es llamado un “ Ajuste de red con control de altura”. Una forma de
desarrollar las nuevas ecuaciones de observación es simplemente establecer las alturas y
correcciones de coordenadas astronómicas como cero. Entonces tenemos (Rapp, 1983,
pág. 156) direcciones de sección normal (Di):
v D = A0 − ( AI 0 + Di − DI ) − Z + d1 dϕ1 + d 2 dλ2 + d 4 dϕ2 + d5 dλ2 (9.27)
Donde AI0 es el acimut astronómico aproximado de una línea inicial. Los coeficientes de
la ecuación de observación son d 1 , d 2 , d 4 , d 5 . La ecuación de distancia de la cuerda
podría ser:
vc = c 0 − cOBS + f1 dϕ1 + f 2 dλ1 + f 4 dϕ2 + f 5 dλ2 (9.28)
Bowring (1980) y Vincenty (1980) dan los coeficientes de la ecuación de observación
para los nuevos modelos cuando la forma general es escrita como sigue:
v = F ( X 0 ) − LOBS + Fdu1 + Gdv1 − F du2 − G dv 2 (9.29)
donde:
du = (M + h)dϕ
(9.30)
dv = (N + h ) cos ϕdλ
El sistema de alturas controladas tiene cierto número de ventajas sobre el sistema clásico
usado por muchos años. Quizás el más importante es que no se desarrollan reducciones
sobre las observaciones para llevarlas al elipsoide. Los acimut son considerados con
respecto a la dirección del vector gravedad y las distancias son consideradas como
cuerdas entre las estaciones. Una segunda ventaja es que el esfuerzo de cálculo es
reducido en los nuevos modelos debido a que se necesitan pocas funciones
trigonométricas.
198

208. 10 DATUM GEODÉSICOS Y ELIPSOIDES DE REFERENCIA
10.1 Desarrollo de los Datums
El propósito de este capítulo es introducir, resumidamente, el tema de los datums
geodésicos y considerar su uso y unificación hoy en día. Los procedimientos para las
actuales definiciones de datums y la determinación de los parámetros elipsoidales es
descrito en Rapp (1983).
Históricamente, los datums geodésicos han sido necesarios para el desarrollo de redes
geodésicas. Estos datums usualmente proveen un punto inicial (ϕ0 , λ0 ), un acimut inicial
(α0 ) para fines de orientación, y parámetros del elipsoide. Para la simple definición de un
datum geodésico son requeridos solamente cinco parámetros.
La ascendente necesidad de control geodésico provocó que varios países desarrollaran
sus propios datums. La obtención de datos más completos y confiables permitió que
nuevos datums geodésicos fuesen definidos en forma más precisa. Algunos datums
fueron definidos con parámetros elipsoidales de modo que las deflexiones
astrogeodésicas pudieran ser pequeñas en un país. Datums pequeños (por ejemplo en
islas) fueron definidos solamente a través de coordenadas astronómicas con parámetros
elipsoidales tomados desde un origen no relacionado. Una lista de 58 datums geodésicos
es dada en Rapp (1983).
La determinación de parámetros elipsoidales ha sido activamente llevada a cabo desde el
siglo XIX. Las técnicas para esos cálculos han usado una gran variedad de datos,
incluyendo el análisis de las redes de triangulación, variaciones de la gravedad, posición
de estaciones derivadas de satélites y altimetría por satélite. En 1909 la precisión formal
en la determinación del radio ecuatorial estuvo en el orden de 18 m (Hayford, 1910)
aunque el valor calculado tenía un error de 252 m. Hoy día, usando variadas técnicas de
medición el radio ecuatorial de la tierra es conocido con un error de ± 1 m. A este nivel
de precisión y mejores se torna importante tener definiciones precisas del significado de
los parámetros elipsoidales. Tales definiciones son descritas por Rapp (1983). La Tabla
(10.1) entrega parámetros de varios elipsoides usados en el pasado y de aquellos actuales.
En algunos casos el achatamiento no está específicamente definido pero es derivado
usando otras cantidades. Por ejemplo, los parámetros del elipsoide de Clark 1866 son
definidos en términos de a y b. El achatamiento de los elipsoides de los Sistemas de
Referencia Geodésicos es derivado de otros datos, primeramente los armónicos zonales
de segundo grado del campo gravitacional de la Tierra que es precisamente definido a
través del análisis del movimiento de los satélites. Para la Asociación Internacional de
Geodesia, las estimaciones listada en esta tabla son las mejores estimadas al igual que los
datos dados. Estas no son usadas para la definición de nuevos juegos de constantes.
199

209. Tabla 10.1 Parámetros Elipsoidales
Nombre del Elipsoide Año Cálculo Semi-eje Mayor Achatamiento
a (m) 1/f
Airy 1830 6377563,396 299,324964
Bessel 1841 6377397,155 299,152813
Clarke 1866 6378206,400 299,978698
Clarke (modificado) 1880 6378249,145 293,466300
Clarke 1880 6378249,145 293,465000
Everest 1830 6377276,345 300,801700
Internacional 1924 6378388,000 297,000000
Krassovski 1940 6378245,000 298,300000
Mercury 1960 6378166,000 298,300000
Mercury (modificado) 1968 6378150,000 298,300000
Nacional Australiano 6378160,000 298,250000
Sudamericano 1969 6378160,000 298,250000
Sistema de Referencia 1967 6389160,000 298,2471674273
Geodésico
WGS72 1972 6378135,000 298,260000
Asociación Internacional 1975 6378140 ± 5 298,257 ± 0,0015
de Geodesia
Sistema de Referencia 1980 6378137,000 298,257222101
Geodésico
Asociación Internacional 1983 6378136 ± 1 298,257000
de Geodesia
WGS84 1984 6378137,000 298,257223563
Asociación Internacional 1987 6378136,000
de Geodesia
10.2 Transformación de Datum
Históricamente, una de las reconocidas metas de la geodesia ha sido la obtención de
coordenadas geodésicas en un sistema común. Este es un procedimiento difícil dado la
cantidad de datum diferentes existentes en el mundo. Sin embargo, usando técnicas
satelitales es posible determinar coordenadas rectangulares de un punto en un sistema
coordenado definido que está cerca de ser geocéntrico. Si se adopta un juego de
parámetros elipsoidales, las coordenadas rectangulares pueden ser convertidas a latitud,
longitud y altura sobre el elipsoide de referencia. Si efectuamos observaciones satelitales
en un punto cuyas coordenadas están definidas en un datum específico podemos
comparar las coordenadas satelitales y las coordenadas del datum para obtener una
conexión entre ambos sistemas.
200

210. Por simplicidad asumimos que el datum de nuestro sistema de coordenadas y el sistema
satelital tienen un origen distinto pero sus ejes X, Y, Z son paralelos, según es mostrado
en la Figura (10.2)
ZD
Zs P
YD
Ys
∆Z
XD ∆X
∆Y
Xs
Figura 10.2 Sistema Satelital (S) y Datum (D) con Ejes Paralelos
Consideremos las coordenadas rectangulares de un punto P en el sistema de datum. Tales
cantidades pueden ser calculadas desde la ecuación (3.152) donde h es la suma de la
altura ortométrica (H) y la ondulación astrogeodésica (NAG):
X D = ( N + H + N AG ) cos ϕcos λ
YD = ( N + H + N AG ) cos ϕsin λ (10.1)
( ( ) )
Z D = N 1 − e 2 + H + N AG sin ϕ
Dejemos que ∆X , ∆Y , ∆Z sean el desplazamiento de datum con respecto al sistema
satelital, así:
X S = X D + ∆X
YS = YD + ∆Y (10.2)
Z S = Z D + ∆Z
El desplazamiento de datum puede ser obtenido con un número suficiente de estaciones
donde las coordenadas son determinadas en ambos sistemas. Si entonces vamos a un
201

211. punto arbitrario y encontramos las coordenadas satelitales podremos sustraer el
desplazamiento de datum para obtener las coordenadas del sistema de datum. Estas
coordenadas pueden ser convertidas a coordenadas geodésicas usando los procedimientos
descritos en la sección (6.8) donde son usados los parámetros del datum elipsoidal.
Los modelos de datum convencional representados por la ecuación (10.2) son basados en
la suposición de que los ejes de los dos sistemas son paralelos, que los sistemas tienen la
misma escala y que la red geodésica ha sido calculada consistentemente. En la realidad
ninguna de estas suposiciones es verdadera, luego los valores de ∆X , ∆Y , ∆Z pueden
variar desde un punto a otro tal como es mostrado por Leick y van Gelder (1975) para
Estados Unidos. Una transformación más general involucra siete parámetros: tres
traslaciones, tres rotaciones representando la ausencia de paralelismo de los ejes de los
dos sistemas y un factor de escala representando la diferencia de escala entre ambos
sistemas. Esta transformación más general puede ser representada como sigue:
X  X   ∆X   X   0 ωZ − ωY   X 
           
 Y  =  Y  +  ∆Y  +  Y  ⋅ ∆L +  − ωZ 0 ωX  ⋅  Y  (10.3)
Z        ω 0   Z D
  S  Z  D  ∆Z   Z  D  Y − ωX   
En esta ecuación ∆L es un parámetro de diferencia de escala y ωX, ωY, ωZ son las
rotaciones sobre los ejes X, Y, Z para lograr el paralelismo con los ejes del sistema
satelital. El desarrollo de la ecuación (10.3) y aplicaciones de esta transformación son
revisadas en Rapp (1983).
Si deseamos adoptar el modelo de transformación simplificado representado por la
ecuación (10.2), podríamos utilizar los valores de desplazamiento de datum para ir desde
un datum local al WGS84 (DMA, 1987). La Tabla (10.2) muestra los tres
desplazamientos del origen de seleccionados datums para ir del sistema local al WGS84.
202

212. Tabla 10.2 Parámetros de Transformación de Sistema Geodésico Local a WGS84
(tomado del DMA TR 8350.2, 1987)*
Datums Geodésicos Constantes
(Elipsoides de Referencia) ∆X (m) ∆Y (m) ∆Z (m) ∆a (m) ∆f ×10 4
Arc 1950 -143 -90 -294 -112,45 -0,54750714
(Clarke 1880)
Geodésico Australiano -134 -48 149 -23 -0,00081204
1984
(Nacional Australiano)
Cape -136 -108 -292 -112,45 -0,54750714
(Clarke 1880)
Europeo 1950 -87 -98 -121 -251 -0,14192702
(Internacional)
India 214 836 303 860,655 0,28361368
(Everest)
Tokio -128 481 664 739,845 0,10037483
(Bessel 1841)
Sudamericano 1969** -75 -1 -44 -23 -0,00081204
(Sudamericano 1969)
Provisorio Sudamericano -251 -0,14192702
1956**
(Internacional 1924)
Cercano a 19° Latitud Sur -270 ± 25 183 ± 25 -390 ± 25
Cercano a 43° Latitud Sur -305 ± 20 243 ± 20 -442 ± 20
Hito XVIII 1963** -251 -0,14192702
(Internacional 1924)
Cercano a 53° Latitud Sur 16 ± 25 196 ± 25 93 ± 25
*
Departamento de Defensa, Sistema Geodésico Mundial 1984, Sus Definiciones y
Relaciones con Sistemas Geodésicos Locales, DMA TR 8350.2, Washington, D.C.,
1987.
** Parámetros para Chile
203

213. BIBLIOGRAFÍA
Ashkenazi, V., Models for controlling National and Continental Networks,
Bulletin Geodesique, 55, 1981.
Ashkenazi, V., and S. Grist, 3-D Geodetic Network Adjustment Models:
Significance of Different Approaches, in Proc. 1983 General Assembly,
International Association of Geodesy, published by Department of
Geodetic Science and Surveying, The Ohio State University, Columbus,
1984.
Badi, K., Report on the Program Bowring Short Lines, Direct and Inverse,
Department of Geodetic Science and Surveying, The Ohio State
University, 1983.
Baeschlin, C.F., Textbook of Geodesy, Orell Füssli Verlag, Zurich, 1984.
Bagratuni, G.V., Course in Spheroidal Geodesy, 1962, translated from Russian,
Translation Division, Foreign Technology Division, Wright-Patterson
AFB, Ohio AD65 520, 1967.
Bartelme, N. and P. Meissl, Ein einfaches, rasches und numerisch stabiles
Verfahren zur Bestimmung des kurzesten Abstandes eines Punktes von
einem spharoidischen Rotationsellipsoid, Allegemeine Vermessungs-
Nachrichter, Vol. 12, pp. 436-439, 1975.
Bomford, G., Geodesy, Oxford at the Clarendom Press, 4th edition, 1980.
Bowring, B., Transformation from Spatial to Geographical Coordinates, Survey
Review, XXIII, 181, pp. 323-327,1976.
Bowring, B., Notes on Space Adjustment Coefficients, Bulletin Geodesique, 54,
191-200, 1980.
Bowring, B.R., The Direct and Inverse Problems for Short Geodesic Lines on the
Ellipsoid, Surveying and Mapping, Vol. 41, N° 2, 135-141, 1981.
Bowring, B.R., The Direct and Inverse Solutions for the Great Elliptic Arc,
Bulletin Geodesique, Vol. 58, 1984.
Carroll, D., and C. Wessells, A 1975 Astrogeodetic Geoid for the United States,
presented at the XVI General Assembly, International Association of
Geodesy, Grenoble, France, 1975.
Clarke, A.R., Geodesy, Oxford at Clarendon Press, 1980.
Clarke, David, Plane and Geodetic Surveying, Volume Two: Higher Surveying,
Constable and Co. Ltd, London, 1957.
DMA, Index of Grid, Datums and Spheroids, 1982, prepared by the Defense
Mapping Agency Hydrographic/Topographic Center, Washington, D.C.
204

214. 20315, in Grids and Grid References, Technical Manual TM 5-241-1,
Dept. of the Army, Washington, D.C., 25 March 1983.
Fisher, I., et al. Geoid Charts of North and Central America, Army Map Service
Technical Report N° 62, Washington, D.C. October 1967.
Fisher, I., The Figure of the Earth – Changes in Concepts, Geophysical Survey, 2,
3-54, 1975a.
Fisher, I., Another Look at Eratosthenes’ and Posidonius’ Determinations of the
Earth’s Circumference, Q. J1. R. Astr. Soc., 16, 152-167, 1975b.
Gan’shin, V.N., Geometry of the Earth Ellipsoid, Nedra Publishers, 1967,
translated from Russian, 1969, ACIC-TC-1473, AD 689507, available
from Clearinghouse, Springfield, Virginia 22151.
Grafarend, E., and B Richter, The Generalized Laplace Condition, Bulletin
Geodesique, 51, 287-293, 1977.
Grushinskiy, N.P., The Theory of the Figure of the Earth, 1963, translated from
Russian, 1969, FTD-HT-23-313-68, AD694748, available from
Clearinghouse, Springfield, Virginia 22151.
Gupta, R.M., A Comparative Study of Various Direct and Inverse Formulae for
Lines up to 800 km in Ellipsoid Geodesy, M.S. thesis, The Ohio State
University, 1972.
Hayford, J., Supplementary Investigation in 1909 of the Figure of the Earth and
Isostasy, U.S. Coast and Geodetic Survey, Washington, D.C., 1910
Heikkinen, M., Geschlossene Formeln Berechnung räumlicher geodätischer
Koordinaten aus rechtwinkligen Koordinaten, Zeitschrift fur
Vermessungswesen, Vol. 5, 207-211, 1982.
Heiskanen, W., and H. Moritz, Physical Geodesy, W.A. Freeman, San Francisco,
1967.
Helmer, F.R., Die Mathematischen Und Physikalischen Theorium Der Hoheren
Geodasie, B.G. Teubner, Leipzig, 1880 (reprinted 1962), (translation by
Aeronautical Chart and Information Center, St. Louis, 1964).
Hirvonen, R., and Moritz, Practical Computations of Gravity at High Altitudes,
Report N° 27, Institute of Geodesy, Photogrammetry and Cartography,
The Ohio State University, Columbus, 1963.
Hosmer, G., Geodesy, John Wiley and Sons, New York, second edition, 1930.
Howse, D., Greenwich Time and the discovery of the longitude, Oxford
University Press, Oxford, England, 1980.
th
Jordan-Eggert, Jordan’s Handbook of Geodesy, translation of 8 edition, 1941 by
Martha W. Carta, (U.S. Army Map Service, Washington, D.C., 1962).
Lambert, W.D. and C. Swick, Formulas and Tables for the Computation of
Geodetic Positions on the International Ellipsoid, Special Publication N°
200, U.S. Coast and Geodetic Survey, Washington, D.C., 1935.
205

215. Lauf, G., Geodesy and Map Projections, TAFE Publications Unit, 37 Long-ridge
St., Collingwood, Victoria 3066, Australia, 1983.
Leick, A., and B. van Gelder, On Similarity Transformations and Geodetic
Network Distortions Based on Doppler Satellite Observations, Report N°
235, Department of Geodetic Science, The Ohio State University,
Columbus, 1975.
Lewis, E.A., Parametric Formulas for Geodesic Curves and Distances on a
Slightly Oblate Earth, Air Force Cambridge Research Laboratories, Note
N° 63-485, April, 1963, AD412 501.
Meade, B.K., Comments on Formulas for the solution of Direct and Inverse
Problems on Reference Ellipsoids Using Pocket Calculators, Surveying
and Mapping, Vol. 41, N° 1, 1981.
Moose, E.R. and S.W. Henriksen, Effect of Geoceiver Observations Upon the
Classical Triangulation Networks, NOAA Technical Report, NOS 66
NOS2, Rockville, Maryland, 1976.
Moritz, H., The Definition of a Geodetic Datum, in Proc., Second Int. Symposium
on Problems Related to the Redefinition of North American Geodetic
Networks, Supt. Of Documents, U.S. Govt. Printing Office, Stock N° 003-
017-0426-1, Washington, D.C. 20402.
Mueller, I.., Spherical and Practical Astronomy as Applied to Geodesy, F. Ungar
Publishing Co., New York, 1969.
Mueller, I., Reference Coordinate Systems for Earth Dynamics. A Preview, in
Proc. Reference Coordinate Systems for Earth Dynamics, D. Reidel
Publishing Co., Boston, 1981.
Olliver, S.G., Observation Equations for Observed Directions and Distances in
Spheroidal Co-ordinates, Survey Review, XXIV, 184, 71-77, 1977.
Paul, M.K., A Note on Computation of Geodetic Coordinates from Geocentric
(Cartesian) Coordinates, Bulletin Geodesique, N° 108, 135-139, June
1973.
Petty, J.E., and W.E. Carter, Uncertainties of Astronomic Positions and Azimuth,
in Proc., Second Int. Symp. On Problems Related to the Redefinition of
North American Geodetic Networks, NOAA, Stock N° 003-017-0426-1,
Superintendent of Documents, Washington, D.C. 20402.
Pick, M., J. Picha, and V. Vyskocil, Theory of Earth’s Gravity Field, Elsevier
Scientific Publishing Co., New York, 1973.
Rapp, R.H., Geometric Geodesy, Volume II (Advance Techniques), Department
of Geodetic Science and Surveying, The Ohio State University, Columbus,
1983.
Robbins, A.R., Geodetic Astronomy in the Next Decade, Survey Review, XXIV,
185, 99-108, 1977.
206

216. Schwartz, C., Deflections of the Vertical, ACSM Bulletin, 65, 17-18, May 1979.
Seppelin, T., The Department of Defense World Geodetic System 1972, The
Canadian Surveyor, Vol. 28, N° 5, 496-506,1974a.
Seppelin, T., The Department of Defense World Geodetic System 1972, presented
at the International Symposium on Problems Related to the Redefinition of
North American Geodetic Networks, University of New Brunswick,
Fredericton, New Brunswick, 1974b.
Smith, J.R., Introduction to Geodesy, The History and Concepts of Modern
Geodesy, J. Wiley & Sons, Inc., 1997.
Thomson, D.B., and P. Vanicek, Note on Reduction of Spatial Distances to a
Reference Ellipsoid, Survey Review, XXII, 173, 309-312, 1974.
Tobey, W.M., Geodesy, Publication 11, Geodetic Survey of Canada, Ottawa,
1928.
Torge, W., Geodesy, pág. 1, 2nd Edition, W de Gruyter, New York, 1991.
Vanicek, P., and E. Krakiwsky, Geodesy, the Concepts, North-Holland Publishing
Col, New York, 1982.
Vanicek, P., and Carrera, How much does reference ellipsoid misalignment affect
deflection components and geodetic azimuth, Canadian Surveyor, 1983.
Vicenty, T., A Note on Reduction of Measured Distances to the Ellipsoid, Survey
Review, XXIII, N° 175, 40-42, 1975.
Vincenty, T., Closed Formulas for the Direct and Reverse Geodetic Problems,
Bulletin Geodesique, 51, 241-242, 1977.
Vincenty, T., Zur räumlich-ellipsoidischen Koordinaten-Transformation,
Zeitschrift fur Vermessungswesen, Vol. 11, N° 105, pp. 519-521, 1980a.
Vincenty, T., Height Controlled Tree-Dimensional Adjustment of Horizontal
Networks, Bulletin Geodesique, 54, 37-43, 1980b.
Vincenty, T., Methods of Adjusting Space System Data and Terrestrial
Measurements, Bulletin Geodesique, 56, 231-241, 1982.
Vincenty, T., On the Role of Rotation Angles in Geodetic Problems, unpublished
manuscript, 6 March 1983.
Wenzel, H.G., Astrogeodetic Geoid Around the North Sea, in Report N° 80
Wissenschaftliche Arbeiten der Lehrstuhle für Geodasie, Photo., und
Kart., Technischen Universital Hannover, Hannover: FRG, 1978.
Zakatov, P.S., A Course in Higher Geodesy, Translated from Russian 1962, by
Israel Program for Scientific Translation, for National Science Foundation,
OST 61-31212.
207