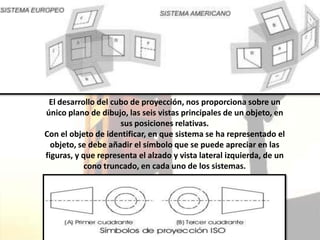
El documento trata sobre la geometría descriptiva, que permite representar objetos tridimensionales en un plano bidimensional. Describe los dos modelos de geometría descriptiva, las proyecciones ortogonales y cómo se pueden obtener las seis vistas principales de un objeto a través de la proyección en los planos horizontal, vertical y de perfil. También explica las diferencias entre los métodos europeo y americano de proyección.

1. GEOMETRIA
DESCRIPTIVA

2. La geometría descriptiva es un conjunto de técnicas de carácter
geométrico que permite representar el espacio tridimensional
sobre una superficie bidimensional y, por tanto, resolver en dos
dimensiones los problemas espaciales garantizando la
reversibilidad del proceso a través de la adecuada lectura.
En la época actual se reconocen dos modelos: uno que considera
la geometría descriptiva como un lenguaje de representación y sus
aplicaciones, y otro que la sitúa como un tratado de geometría.
Aunque no es exactamente lo mismo, su desarrollo ha estado
asociado al de la Geometría proyectiva.

3. La geometría
La geometría es la parte de las matemáticas que estudia las propiedades y
las medidas de las figuras en el plano o en el espacio.
Se distinguen varias clases de geometría:
•Geometría algorítmica: aplicación del álgebra a la geometría para
resolver por medio del cálculo ciertos problemas.
•Geometría analítica: estudio de figuras que utiliza un sistema de
coordenadas y los métodos del análisis matemático.
•Geometría plana: parte de la geometría que considera las figuras cuyos
puntos están todos en un plano.
•Geometría del espacio: la que considera las figuras cuyos puntos no están
todos en un mismo plano.
•Geometría descriptiva: la que tiene por objeto resolver los problemas de la
geometría del espacio por medio de operaciones efectuadas en un plano
y representar en él las figuras de los sólidos.
•Geometría proyectiva: la que trata de las proyecciones de las figuras sobre
un plano.

4. Formas geométricas
Clasificación de las formas geométricas más elementales: Formas
geométricas planas:
•Recta
•Polígonos
•Las secciones cónicas
Formas geométricas espaciales:
Superficies regladas:
•Poliedros Regulares:
•Pirámide
•Cuña
•Prisma
Superficies de revolución:
•Cilindro
•Cono
•Esfera
•Elipsoide
•Paraboloide
•Hiperboloide
Superficies no regladas

5. Aplicaciones
Toda disciplina que requiera la representación de elementos en una
superficie plana (papel) encontrará, en la Geometría Descriptiva, un gran
aliado. Es por esto que la Geometría Descriptiva se encuentra en todos los
planes de estudios de Ingeniería, Arquitectura, Diseño, Topografía, entre
otras. Una parte de ella estudia la Proyección Acotada, en la cual se basan
los planos topográficos y de obras públicas, los cuales son trazados e
interpretados normalmente por topógrafos.
Como asignatura de estudio obligatorio en las escuelas de ingeniería y
arquitectura del mundo entero, el estudio de la Geometría Descriptiva
persigue el desarrollo intelectual del estudiante en dos campos distintos pero
complementarios: la comprensión del espacio tridimensional que rodea al
individuo y el desarrollo de una estructura de pensamiento lógica, lo cual
permite al profesional sentar las bases de otras disciplinas, como la
mecánica de cuerpos rígidos, deformables y fluidos, enfrentando, al mismo
tiempo, los problemas específicos de su área según un enfoque heurístico,
no memorístico, de la realidad objeto de estudio.
Pudiera afirmarse que la Geometría Descriptiva es al ejercicio profesional del
diseñador lo que la gramática es al idioma (palabras de Harry Osers). Como
medio de expresión, requiere de una claridad y rigurosidad excepcional.
Bien dice el refrán: una imagen dice más que mil palabras.

6. PROYECCIONES ORTOGONALES*
Se denominan proyecciones ortogonales
al "sistema de representación" que nos
permite dibujar en diferentes planos un
objeto situado en el espacio.
Cuando hablamos de
"sistemas de representación"
nos referimos a un método,
código o conjunto de normas
preestablecidas que
posibilitan transmitir ideas
graficas.

7. Este sistema esta basado en la utilización de la menor cantidad de
elementos que nos permita configura la realidad tridimensional. Esto
es posible a partir de considerar el espacio real como el encuentro de
un plano recto horizontal (P.H) y otro vertical (P.V) que se cortan entre
si formando un ángulo de 90 grados, por lo que son perpendiculares.
En teoría estos planos son infinitos, aunque en la practica se limitan de
acuerdo a la necesidad del trabajo. la única definición real de ambos
es la línea producida por su intersección.

8. MONTEAS!*
Montea: Pirámide Cuadrangular
Montea: Cilindro

9. Montea: Plano representado…
“Dorito”

10. MONTEAS Del un plano
interceptado por otros*

14. TEORÍA DE LA PROYECCIÓN
Si situamos un observador según las seis
direcciones indicadas por las flechas,
obtendríamos las seis vistas posibles de un
objeto.
Estas vistas reciben las siguientes
denominaciones:
Vista A: Vista frontal o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior
Hay tres planos principales de proyección:
horizontal, vertical y de perfil. Estos planos
se intersecan uno a otro en ángulo recto
formando el primero, segundo, tercero y
cuarto ángulos o cuadrantes. Técnicamente
se puede proyectar un objeto en cualquiera
de estos cuadrantes.

15. Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos
variantes de proyección ortogonal de la misma importancia:
- El método de proyección del primer diedro, también denominado Europeo
(antiguamente, método E)
- El método de proyección del tercer diedro, también denominado Americano
(antiguamente, método A)
En ambos métodos, el objeto se supone dispuesto dentro de un cubo, sobre cuyas
seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.
La diferencia esta en que, mientras en el sistema Europeo, el objeto se encuentra
entre el observador y el plano de proyección, en el sistema Americano, es el plano de
proyección el que se encuentra entre el observador y el objeto.

16. Una vez realizadas las seis proyecciones ortogonales sobre las
caras del cubo, y manteniendo fija la cara de la proyección del
alzado (A), se procede a obtener el desarrollo del cubo, que como
puede apreciarse en las figuras, es diferente según el sistema
utilizado.

17. El desarrollo del cubo de proyección, nos proporciona sobre un
único plano de dibujo, las seis vistas principales de un objeto, en
sus posiciones relativas.
Con el objeto de identificar, en que sistema se ha representado el
objeto, se debe añadir el símbolo que se puede apreciar en las
figuras, y que representa el alzado y vista lateral izquierda, de un
cono truncado, en cada uno de los sistemas.