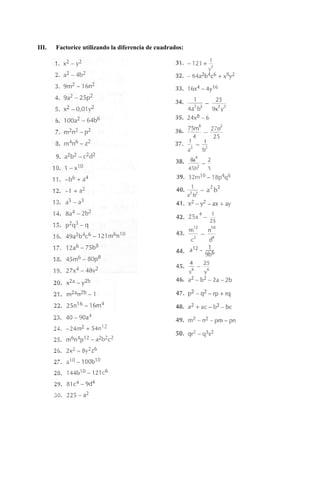Este documento presenta una guía de trabajo para estudiantes de preuniversitario sobre factorización algebraica. Explica diferentes métodos de factorización como factor común, diferencia de cuadrados, trinomio ordenado y sumas/diferencias de cubos. Luego presenta ejercicios para que los estudiantes apliquen estos métodos de factorización.

1. Preuniversitario FEUNAP
Prof. Judith Zarate Fernández
Área de Matemáticas
Unidad: Algebra
Contenido: Factorización
GUIA DE TRABAJO Nº12
Nombre: ____________________________________ Paralelo: _________ Fecha: ___________
Objetivo: Contribuir al planteamiento del lenguaje algebraico. Utilizar las propiedades de los Reales
para resolver los problemas u ejercicios que se proponen.
Instrucciones: Esta guía contiene Ítems de desarrollo, los tiempos estimados por ítem serán
dados por el profesor a cargo de la clase. Toda respuesta debe ser escrita en el mismo material
dejando una constancia del procedimiento utilizado. Esta guía de trabajo es para uso exclusivo
del preuniversitario se pide total responsabilidad de dicho material.
Definición
Factorización : llamaremos Factorización al producto expresado por monomios o polinomios
que generen la expresión Algebraica.
Factor termino Común: llamaremos término común al producto expresado por el factor numérico y
factor literal en común con el menor grado contenido por todo los términos de la expresión
Algebraica.
Factor común compuesto: llamaremos factor común compuesto al asociar términos en grupo que
contengan términos en común. Si los términos reducidos son los mismos, se factoriza el
polinomio dejando como resultado el producto de dos polinomios.
Diferencia de cuadrados: llamaremos diferencia de cuadrados al producto de una suma por su
diferencia si la expresión algebraica contiene dos términos al cuadrado cuya operación
es la resta.
Trinomio ordenado: llamaremos trinomio ordenado si la expresión tiene la forma ax2
± bx ± c , que
expresaremos como el producto de dos binomios por medio del siguiente proceso:
 si el primer termino esta al cuadrado entonces √ ax2
será el termino en común de
los binomios
 el segundo termino de los binomios deben cumplir lo que el producto de los
términos es igual a c y la suma de los términos es igual a b.
Sumas o Diferencias de cubos: llamaremos suma o diferencias de cubo a la expresión de dos
términos al cubo, expresaremos el producto de polinomios de la siguiente forma:
 si la operación de la suma entonces quedaran como
x3
+ y3
= ( x – y )( x2
+ xy + y2
)
 si la operación es la resta entonces quedara como
x3
– y3
= ( x + y )( x2
– xy + y2
)

2. I. Factorice las siguientes expresiones:

3. II. Factorice utilizando el Factor común compuesto:

4. III. Factorice utilizando la diferencia de cuadrados:

5. IV. Factorice utilizando el trinomio ordenado:

6. V. Factorice utilizando la sumas o diferencias de cubos: