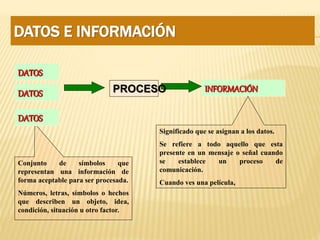
Este documento proporciona una introducción a los conceptos fundamentales de la estadística. Define la estadística como la rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos para resolver problemas y tomar decisiones. Explica que la estadística tiene tres funciones principales: recolección, organización, presentación, análisis e interpretación de datos. Además, clasifica la estadística en descriptiva e inferencial, y señala que la estadística es aplicable a cualquier campo cientí