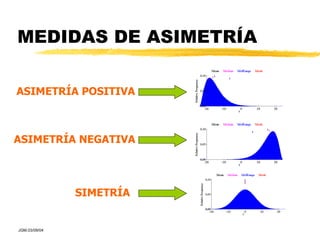
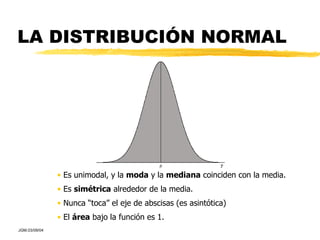
Este documento describe diferentes técnicas estadísticas descriptivas para variables cualitativas y cuantitativas. Para variables cualitativas, solo se pueden hacer recuentos y calcular porcentajes. Para variables cuantitativas, se describen medidas de posición (media, mediana, moda), dispersión (varianza, desviación estándar, coeficiente de variación) y asimetría, así como representaciones gráficas como el histograma. La distribución normal es un ejemplo común de función de densidad de probabilidad.