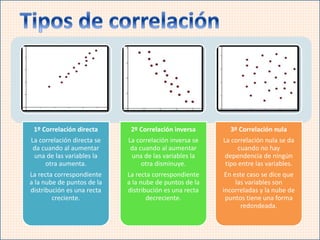
Este documento describe conceptos estadísticos bidimensionales. Explica que una distribución bidimensional representa la relación entre dos variables a través de una nube de puntos, y que la correlación entre las variables puede ser directa, inversa o nula. También cubre conceptos como distribuciones marginales y condicionadas, covarianza, coeficiente de correlación lineal y rectas de regresión.

1. PHA

4. Se habla de estadística bidimensional
cuando dos variables X e Y están relacionadas
estadísticamente cuando conocida la primera se
puede estimar aproximadamente el valor de la
segunda.
Si representamos cada par de valores como
las coordenadas de un punto, el conjunto de
todos ellos se llama nube de puntos o diagrama
de dispersión.

6.  Tabla de doble entrada: Está formada por tantas filas como valores
tengamos de la variable Y, así como tantas columnas como valores tengamos
de la variable X, y una fila y una columna más para indicar los totales.
-Está indicada para casos con bastantes datos, en los que para cada
valor de una variable, existen varios valores de la otra.
-En el caso de que alguna de las variables sea continua, aparecerán los
distintos intervalos en la correspondiente fila o columna y otra fila o columna
más con las marcas de clase de cada intervalo.

8. Una nube de puntos o diagrama de dispersión es
la representación de cada par de valores de una
distribución bidimensional (xi, yi) como las coordenadas
de un punto.
Sobre la nube de puntos puede trazarse una recta
que se ajuste a ellos lo mejor posible, llamada recta de
regresión.

10. La correlación estadística determina
la relación o dependencia que existe entre
las dos variables que intervienen en una
distribución bidimensional.
En caso de que suceda, diremos que
las variables están correlacionadas o que
hay correlación entre ellas.

11. 1º Correlación directa
La correlación directa se
da cuando al aumentar
una de las variables la
otra aumenta.
La recta correspondiente
a la nube de puntos de la
distribución es una recta
creciente.
2º Correlación inversa
La correlación inversa se
da cuando al aumentar
una de las variables la
otra disminuye.
La recta correspondiente
a la nube de puntos de la
distribución es una recta
decreciente.
3º Correlación nula
La correlación nula se da
cuando no hay
dependencia de ningún
tipo entre las variables.
En este caso se dice que
las variables son
incorreladas y la nube de
puntos tiene una forma
redondeada.

13. Distribuciones marginales: son distribuciones
unidimensionales, que pueden analizarse mediante parámetros
estadísticos, que nos informan del número de observaciones para
cada una de las variables, prescindiendo de la información sobre las
demás variables.
-En el caso bidimensional hay dos (una para la x y otra para la y).
-A partir de la tabla de correlación pueden construirse las
distribuciones marginales, asignando a cada valor de la variable
considerada su frecuencia.

14. Distribuciones condicionadas : es el estudio de una de las
variables para un determinado valor de la otra variable.
- Esta relación puede ser de X/Y=yj, o bien, Y/X = xi, según
condicionemos a un valor de una u otra variable.
- Al tratarse de una variable unidimensional podremos estudiar
todos sus parámetros estadísticos
- Esto supone considerar únicamente una columna de la tabla
de correlación (distribución de x condicionada a un valor de y) o
una fila de la tabla (distribución de y condicionada a un valor de x).

16. Asociados a las distribuciones marginales y condicionadas podemos
definir algunos estadísticos de tendencia central o dispersión.
 Las medias marginales de la variable X e Y se definen:
 Las varianzas marginales respectivas son:

17. La covarianza de una variable bidimensional es la media aritmética de los
productos de las desviaciones de cada una de las variables respecto a sus
medias respectivas.
-Se representa por sxy o σxy.
La covarianza indica el sentido de la correlación entre las variables
-Si σxy > 0 la correlación es directa.
-Si σxy < 0 la correlación es inversa.

18. El coeficiente de correlación lineal es el cociente entre la covarianza y el
producto de las desviaciones típicas de ambas variables y se expresa mediante
la letra r.
 Propiedades del coeficiente de correlación
1. No varía al hacer la escala de medición.
2. Su signo es el mismo que el de la covarianza.
3. Es un número real comprendido entre −1 y 1. −1 ≤ r ≤ 1
-Si toma valores cercanos a −1 la correlación es fuerte e inversa,
-Si toma valores cercanos a 1 la correlación es fuerte y directa.
-Si toma valores cercanos a 0, la correlación es débil.
4. Si r vale 1 o −1, los puntos de la nube están sobre la recta creciente o
decreciente. Entre ambas variables habrá dependencia funcional.

20. -La recta de regresión de Y sobre X se utiliza para estimar los valores de la Y a partir de
los de la X.
La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable X.
-La recta de regresión de X sobre Y se utiliza para estimar los valores de la X a partir de
los de la Y.
La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable Y.
La recta de regresión es aquella que se traza sobre la concentración de puntos en el
diagrama de dispersión. Pueden ser: