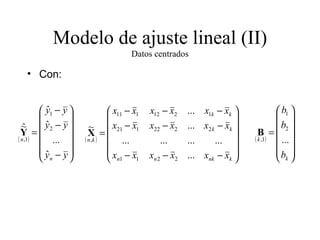
El documento describe el modelo de regresión lineal múltiple, incluyendo variables dependientes e independientes, el proceso de estimación de parámetros para minimizar la suma de los cuadrados de los residuos, y los beneficios de trabajar con datos centrados para simplificar los cálculos.

1. Modelo general de regresión lineal múltiple

2. Variables Y : Variable dependiente Variable endógena Variable explicada X j : Variables exógenas Variables independientes Variables explicativas Sólo una Al menos una

3. Ejemplo de ilustración

4. Ejemplo de ilustración Y : Ingresos del supermercado X 1 : Habitantes del municipio del supermercado X 2 : Superficie del supermercado (m 2 )

5. Tabla de datos Ingresos (Y) Habitantes (X1) Superficie (X2) 198 70 21 209 35 26 197 55 14 156 25 10 85 28 12 187 43 20 43 15 5 211 33 28 120 23 9 62 4 6 176 45 10 117 20 8 273 56 36

6. Modelo de regresión lineal Ejemplo de ilustración Deseamos explicar los ingresos del supermercado ( Y ), mediante la población del municipio ( X 1 ) y la superficie del supermercado ( X 2 ). Si la relación existente entre las variables fuera de tipo lineal utilizaríamos la siguiente expresión:

7. Modelo de regresión lineal (II) Ejemplo de ilustración Pero la relación entre las variables no es necesariamente perfecta. Por ese motivo añadimos un elemento aleatorio a cada observación:

8. Modelo de regresión lineal (III) Ejemplo de ilustración Renta de los habitantes Medio rural o urbano ... Edad promedio de los habitantes Variables que no hemos considerado

9. Modelo de regresión lineal (IV) Ejemplo de ilustración Es el término constante del modelo y es desconocido. Son los coeficientes desconocidos de la combinación lineal. Es el i-ésimo término de error (desconocido)

10. Modelo de regresión lineal (V) Ejemplo de ilustración Es el término constante del modelo y es desconocido. Son los coeficientes desconocidos de la combinación lineal. Es el i-ésimo término de error (desconocido)

11. Modelo de regresión lineal (VI) Ejemplo de ilustración Es el término constante del modelo y es desconocido. Son los coeficientes desconocidos de la combinación lineal. Es el i-ésimo término de error (desconocido)

12. Modelo de regresión lineal (VII) Ejemplo de ilustración Este sistema de ecuaciónes: Consta de 13 ecuaciones y 16 incógnitas. Tiene infinitas soluciones. Podemos asignar valores arbitrarios a cualesquiera tres incógnitas y calcular las demás.

13. Especificación del modelo Ejemplo de ilustración Así lo haremos: Nuestro objetivo es que los valores de las incógnitas sean lo más pequeños posible. Determinaremos cuáles son los valores más adecuados de los coeficientes del modelo para alcanzar este objetivo. Llamaremos residuos a los valores que toman las incógnitas en la solución del sistema de ecuaciones.

14. Especificación del modelo(II) Ejemplo de ilustración Dicho de otro modo: queremos encontrar valores concretos para las incógnitas a los que llamaremos Estos valores concretos consiguen que los valores de las incógnitas sean lo más pequeños posible.

15. Especificación del modelo(III) Ejemplo de ilustración Para minimizar los residuos de manera global emplearemos la siguiente expresión: Es decir, debemos encontrar los valores de los coeficientes que minimizan la suma de los cuadrados de los residuos . A este criterio se le llama de los “ mínimos cuadrados ”.

16. Especificación del modelo(IV) Ejemplo de ilustración Deseamos minimizar esta suma

17. Especificación del modelo (V) Ejemplo de ilustración Por tanto, la solución del sistema de ecuaciones será la siguiente: Las incógnitas tomarán los valores . Estos valores consiguen que los valores de las icógnitas sean lo más pequeños posible. Las incógnitas tomarán los valores

18. Modelo de ajuste lineal Ejemplo de ilustración Después de calcular los valores de los parámetros de la combinación lineal, podremos construir el modelo de ajuste lineal : Los valores calculados para la variable dependiente mediante el modelo de ajuste lineal serán los llamados valores estimados .

19. Modelo de ajuste lineal (II) Ejemplo de ilustración A la diferencia entre los valores observados y los valores estimados para la variable dependiente los llamamos residuos:

20. ¡Cuidado! Es muy importante distinguir los residuos de los errores : Los errores son cantidades desconocidas y aleatorias. Miden el efecto de las variables que no hemos tomado en cuenta. Los residuos , por el contrario, son valores conocidos. Miden las diferencias entre los valores observados y los valores estimados de la variable dependiente.

21. Estimación de los parámetros Ejemplo de ilustración Recordemos: Queremos encontrar unos valores concretos para las incógnitas . Estas estimaciones consiguen que los valores concretos de las incógnitas -a los que llamamos - sean lo más pequeños posible.

22. Estimación de los parámetros (II) Ejemplo de ilustración Ecuaciones normales (3 ecuaciones, 3 incógnitas)

23. Estimación de los parámetros (III) Ejemplo de ilustración Empleando matrices:

24. Estimación de los parámetros (IV) Ejemplo de ilustración En nuestro ejemplo de ilustración:

25. Caso general

26. Modelo de regresión lineal Caso general Cuando tenemos más de dos variables explicativas: Empleando matrices:

27. Modelo de regresión lineal (II) Caso general

28. Modelo de regresión lineal (III) Caso general Podemos expresar el modelo de regresión lineal de un modo más sencillo: Modelo de regresión lineal n ecuaciones n+k+1 incógnitas

29. Modelo de regresión lineal (IV) Caso general

30. Especificación del modelo Caso general Nuestro objetivo es conseguir que los valores de las incógnitas sean lo más pequeños posible. Buscaremos los valores de los coeficientes del modelo que resulten los más adecuados de cara a cumplir con el objetivo planteado. A los valores que en la solución del sistema de ecuaciones toman las inógnitas los llamaremos residuos.

31. Especificación del modelo (II) Caso general Expresado de otro modo: Deseamos encontrar un vector , que es un valor concreto del vector . Este vector concreto consigue que los valores de las incógnitas sean lo más pequeños posible.

32. Esepecificación del modelo (III) Caso general Por lo tanto, la solución del sistema de ecuaciones será la siguiente: El vector tomará el valor . Este valor del vector consigue que el valor del vector sea mínimo. El vector tomará el valor

33. Especificación del modelo (IV) Caso general Para minimizar los residuos de manera global emplearemos la siguiente expresión: Es decir, tenemos que encontrar los valores de los coeficientes del modelo que hacen mínima la suma de los cuadrados de los residuos. A este criterio se le da el nombre de “ criterio de los mínimos cuadrados ”.

34. Modelo de ajuste lineal Caso general Cuando tenemos más de dos variables explicativas: Empleando matrices:

35. Modelo de ajuste lineal (II) Caso general Podemos expresar el modelo de ajuste lineal de una forma más sencilla: Modelo de ajuste lineal

36. Modelo de ajuste lineal (III) Caso general

37. Modelo de ajuste lineal (IV) Caso general El valor estimado de la variable dependiente para un individuo será el siguiente: Con:

38. Estimación de los parámetros Caso general Recordemos: Queremos encontrar un vector de valores concretos para el vector . Este vector debe ser tal que minimice globalmente los residuos.

39. Estimación de los parámetros (II) Caso general Teniendo en cuenta que: Derivando respecto a B:

40. Estimación de los parámetros (III) Caso general Igualando la derivada a cero: Si la matriz es no singular:

41. Estimación de los parámetros (IV) Caso general ¿La solución que se ha encontrado consigue minimizar la SCR? Supongamos que es otra solución. Entonces:

42. Datos centrados

43. Modelo de ajuste Datos centrados Cuando las variables explicativas toman sus respectivos valores promedio el valor estimado para la variable dependiente es su media: Es decir, el hiperplano del modelo de ajuste pasa por la media de las variables.

44. Modelo de ajuste (II) Datos centrados Por lo tanto podemos escribir el modelo de ajuste lineal de otro modo: O empleando matrices:

45. Modelo de ajuste (III) Datos centrados Con:

46. Estimación de los parámetros Datos centrados Recordemos: Para encontrar el vector debemos minimizar de manera global los residuos.

47. Estimación de los parámetros (II) Datos centrados Teniendo en cuenta que: Dervando respecto a B:

48. Estimación de los parámetros (III) Datos centrados Igualando a cero la derivada anterior: Si la matriz es no singular:

49. Modelo de ajuste lineal Datos centrados Si trabajamos con datos centrados: y:

50. Modelo de ajuste lineal (II) Datos centrados Con:

51. Modelo de ajuste lineal (III) Datos centrados Para obtener el término constante utilizaremos la siguiente expresión: Por lo tanto:

52. Datos centrados Trabajar con datos centrados supone una gran ventaja: Con datos originales, la dimensión de es ( k +1, k +1). Con datos centrados, la dimensión de es ( k , k ). Por lo tanto, el cálculo de la matriz inversa es más sencillo en el caso de la matriz .

53. Matriz de varianzas y covarianzas

54. Matriz de varianzas y covarianzas

55. Matriz de varianzas y covarianzas

56. Matriz de varianzas y covarianzas

57. Modelo de ajuste lineal Matriz de varianzas y covarianzas

58. Modelo de ajuste Datos centrados