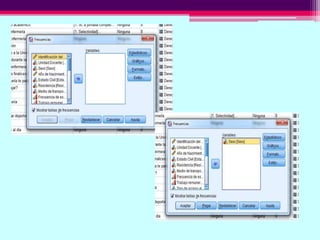
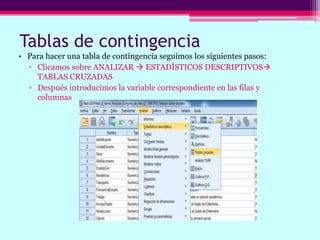
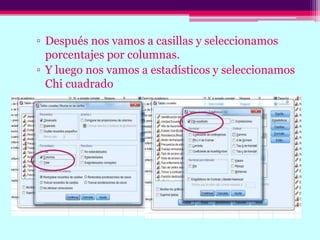
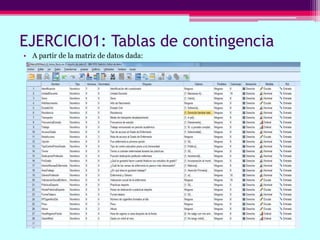
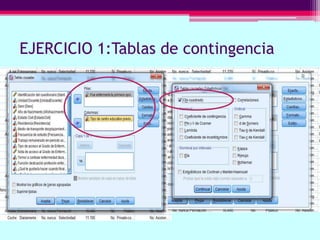
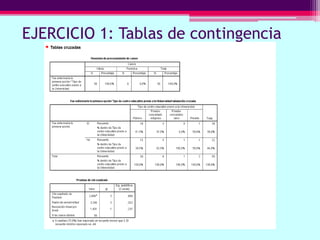
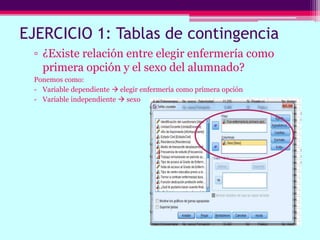
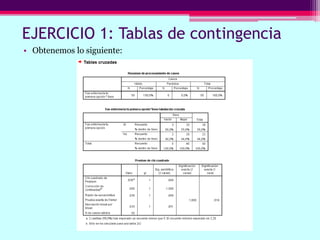
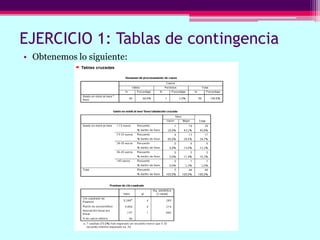
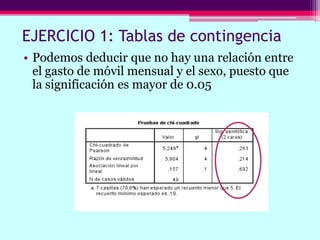
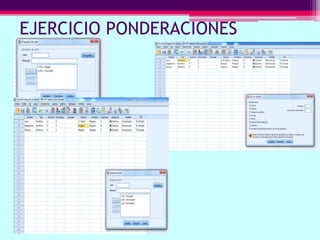
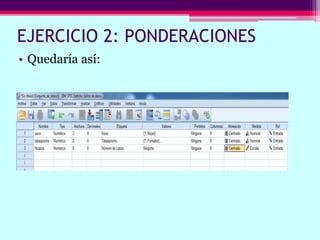
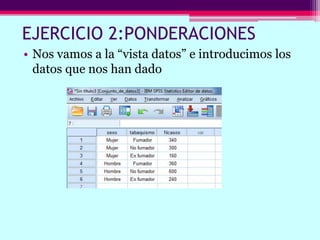
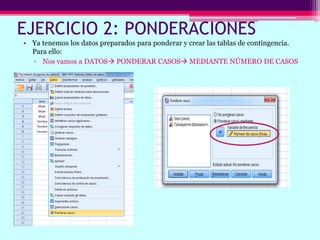
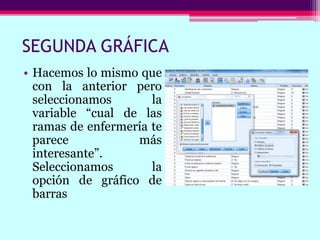
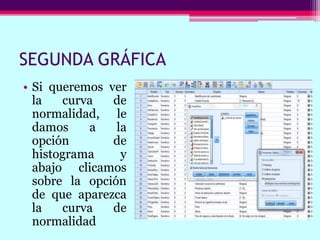
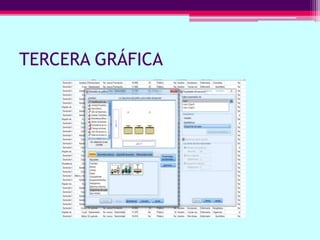
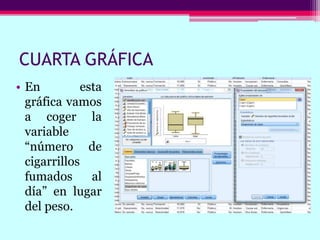
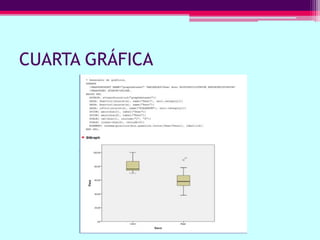
Este documento describe cómo calcular frecuencias y medidas estadísticas básicas como la media, moda y desviación estándar usando SPSS. También explica cómo crear tablas de contingencia para analizar la relación entre variables y realizar pruebas de chi cuadrado. Por último, muestra diferentes tipos de gráficos como diagramas de sectores, barras y diagramas de caja.