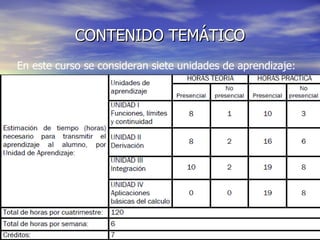
Este documento presenta la introducción y el temario de la asignatura de Cálculo Diferencial e Integral. La asignatura enseña los conceptos y herramientas matemáticas necesarias para que los estudiantes de ingeniería puedan resolver problemas a través de la modelación matemática. El objetivo es desarrollar la capacidad de aplicar el cálculo como herramienta para resolver problemas prácticos de ingeniería. El contenido incluye siete unidades sobre conceptos básicos de la matemática universitaria y el uso de herramientas computacionales

1. CÁLCULO DIFERENCIAL E INTEGRAL INTRODUCCIÓN Y TEMARIO

2. INTRODUCCIÓN El contenido de la asignatura fue diseñado partiendo del mínimo de conceptos y herramientas matemáticas que todo alumno de ingeniería necesita para resolver problemas ingenieriles. La enseñanza del cálculo requiere un énfasis especial en la solución de problemas relacionados con aplicaciones reales sin descuidar el desarrollo conceptual del mismo. La asignatura de Cálculo diferencial e Integral, permite al estudiante modelar procesos o sistemas en base a teoremas fundamentales del cálculo, con el propósito de tomar decisiones con base matemática y resolver problemas relativos a la Ingeniería.

3. La mayoría de algoritmos son aproximaciones que pueden, ocasionalmente, resultar en errores significativos en ciertos tipos de problemas. Al entender como trabajan tales algoritmos se puede anticipar e identificar cuando una computadora proporciona resultados erróneos. Un ejemplo es el halo que se obtiene en las imágenes MRI (Imágenes por Resonancia Magnética), donde una interpretación incorrecta puede llevar a un diagnóstico inadecuado con serias consecuencias sobre el paciente. La resonancia magnética es un procedimiento de diagnóstico que utiliza una combinación de imanes grandes, radiofrecuencias y una computadora para producir imágenes detalladas de los órganos y las estructuras internas del cuerpo.

4. OBJETIVO El objetivo de la asignatura es: “Desarrollar en el alumno las capacidades y habilidades necesarias para aplicar el cálculo, como una herramienta matemática, para solucionar problemas prácticos reales de ingeniería. PRE-REQUISITOS: Despeja variables en ecuaciones Álgebra Conoce las funciones elementales Realiza operaciones con polinomios.

5. JUSTIFICACIÓN: Los contenidos de la asignatura Cálculo Diferencial e Integral, son importantes para poder establecer los nexos necesarios y conceptuales para los futuros cursos de ingeniería. Es necesario además establecer los fundamentos y competencias necesarias para que el ingeniero logre modelar, interpretar y solucionar situaciones de su vida laboral y social de una forma óptima.

6. CONTENIDO TEMÁTICO En este curso se consideran siete unidades de aprendizaje:

7. CAPACIDADES Comprender los conceptos básicos de la matemática universitaria Utilizar el lenguaje de la matemática para expresarse correctamente Formular problemas en lenguaje matemático para facilitar su análisis y solución Utilizar modelos matemáticos para la descripción de situaciones reales Utilizar las herramientas computacionales de cálculo numérico y simbólico en el planteamiento y resolución de problemas

8. Aplicar el razonamiento lógico deductivo para la solución de problemas Aplicar principios, leyes y teorías generales para encontrar soluciones a problemas particulares.

9. BIBLIOGRAFÍA 1. Título: Cálculo Diferencial e Integral Autor: Stewart, J. Año: 2006 Editorial: Thomson (2ª) Lugar: México ISBN o registro: 970-686-127-0 2. Título: Cálculo Autor: Larson, R., Hostetler, R. y Edwards, B. Año: 2005 Editorial: McGraw-Hill Interamericana (8ª) Lugar: México ISBN o registro: 5-88417-028-9 3. Título: Cálculo Autor: Ayres, F., Mendelson, E. Año: 2000 Editorial: McGraw-Hill Lugar: Colombia ISBN o registro: 958-41-0131-5

10. 4. Stewart, J., Cálculo, 4ª. Edición, Thomson, México, 2004. ISBN: 970-686-127-0. 5. Purcell, B., Cálculo, 8ª. Edición, Prentice- Hall, México, 2004. ISBN:970-686-127-0. 6. Piskunov, N., Cálculo Diferencial e Integral, 1ª. Edición. Montaner y Simón, España, 2000. ISBN: 5-88417-028-9 7. Courant, R. y John, F., Introducción al Cálculo y al Análisis Matemático, 1ª.Edición, Limusa, México, 1987. ISBN 968-18-3985 8. Granville, W., Cálculo diferencial e integral, Limusa. ISBN:968-18-1178-X 9. http://www.mathematica-journal.com