Este documento presenta los temas centrales del cálculo diferencial organizados en cuatro unidades. La primera unidad cubre conceptos básicos de funciones como tipos, gráficas y características. La segunda unidad trata sobre límites, incluyendo definiciones, tipos y determinación. La tercera unidad explica la derivada con definiciones, reglas y cálculos. La cuarta unidad analiza la continuidad y discontinuidad de funciones. El documento provee una introducción general al cálculo diferencial.

1. CALCULO DIFERENCIAL

2. UNIDAD 1
1.- FUNCIONES.
1.1.- CONCEPTOS BÁSICOS: DEFINICIÓN, NOTACIÓN Y ELEMENTOS BÁSICOS.
1.2.- GRÁFICAS DE FUNCIONES.
1.3.- TIPOS DE FUNCIONES.
1.4.- CARACTERÍSTICAS DE FUNCIONES: PAR, IMPAR, MONÓTONAS, CRECIENTE Y DECRECIENTE.
1.5.- OPERACIONES CON FUNCIONES.
1.6.- COMPOSICIÓN DE FUNCIONES.
1.7.- FUNCIONES INVERSA.
UNIDAD 2
2.- LÍMITES.
2.1.- DEFINICIONES BÁSICAS DE LÍMITE, NOTACIÓN, INTERPRETACIÓN GEOMÉTRICA.
2.2.- TIPOS DE LÍMITES: DERECHA, IZQUIERDA E INFINITO.
2.3.- LIMITE DE UNA VARIABLE.
2.4.- LIMITE DE UNA FUNCIÓN.
2.5.- PROPIEDADES QUE SE CUMPLEN EN LOS LÍMITES.
2.6.-DETERMINACIÓN DE LÍMITES DE FUNCIONES.

3. UNIDAD 3
3.- DERIVADA
3.1.- DEFINICIONES BÁSICAS Y NOTACIONES.
3.2.- INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA.
3.3.- REGLA GENERAL PARA LA DERIVACIÓN DE FUNCIONES. (REGLA DE LOS 4 PASOS).
3.4.- REGLAS ALGEBRAICAS PARA DERIVAR FUNCIONES.
3.5.- CALCULO DE LA DERIVADA.
3.6.- DERIVADAS DE FUNCIONES IMPLÍCITAS
3.7.- CÁLCULOS DE MÁXIMAS Y MÍNIMAS.
3.8.- APLICACIÓN DE LA DERIVADA
UNIDAD 4
4.- CONTINUIDAD.
4.1.- DEFINICIÓN BÁSICA Y NOTACIÓN.
4.2.- CONTINUIDAD DE UN PUNTO.
4.3.- CONTINUIDAD DE UNA FUNCIÓN.
4.4.- ASOCIACIÓN DE LA CONTINUIDAD.
4.5.- CONTINUIDAD LATERAL.
4.6.- CONTINUIDAD DE LA COMPOSICIÓN DE FUNCIONES.
4.7.- DISCONTINUIDAD.

4. Plano cartesiano
P(-3,4)
Q(7,-3)
R(-5,-6)
L(5,2)
y
X
-y
-X
Producto cartesiano es la multiplicación entre los elementos de dos conjuntos dados.

5. A= {1,3,5} B= {2,4,6}
={ (1,2); (1,4); (1,6)
A x B (3,1); (3,4); (3,6)
}
(5, 2); (5, 4); (5, 6) Las relaciones .- Cuando hay una comparación entre los elementos de dos conjuntos, con una regla fija. La relación sale del
producto.
A= {1,3,5} B= {2,4,6} R: “Mayor que”
Nota.- Los elementos del primer
conjunto se ubican en el
eje de las X, y los del
segundo en el eje de las
Y.
1
3
5
2
4
6
R: A B= {(3,2);(5,4);(5,6)}

6. Función .- Es una relación entre los elementos de dos conjuntos, de tal manera que cada elemento del primer
conjunto le corresponde uno y solo un elemento del segundo conjunto.
Ejemplo:
A= {Estudiante de 3ro de Informática} B= {Numero de calzado de los estudiantes}
Kathy
Xiomi
Marcos
Dario
Alex
Jairo
37
38
40
44
42
Kat Xio Mar Dar Ale Jai
Diagrama de Venn
Forma gráfica
Notación .- Es la representación simbólica de la función y se representa con la siguiente notación: ƒ (x) o ƒ: A B.
Estructura de una función
1.- Una función tiene al menos dos conjuntos.
2.- Una función tiene una regla.

7. 1.a.- Al primer conjunto se lo denomina “conjunto de partida”.
2. a.- Al segundo conjunto se lo denomina “conjunto de llegada”.
1.a.1.- A los elementos que participan en el primer conjunto se los denomina Dominio : Dom ƒ .
2.b.- A los elementos que participan en el segundo conjunto se los denomina “ Rango: Ran ƒ “ o también se le llama
“Imagen: Img ƒ “
Joa
David
Noelly
Raquel
Angel
20
21
23
10
31
ƒ
A B
Joa Dav Noe Raq Ang

8. Tipos de funciones

9. Grafica de funciones
Graficar ƒ (x) = x + 2 x= -4, -2, 0, 2, 4
ƒ (-4) = -4 + 2 = -2
ƒ (-2) = -2 + 2 = 0
ƒ (0) = 0 + 2 = 2
ƒ (1) = 1 + 2 = 3
ƒ (2) = 2 + 2 = 4
ƒ (x) = x
ƒ (-4) = -4
ƒ (-2) = -2
ƒ (0) = 0
ƒ (2) = 2
ƒ (4) = 4
ƒ (x) = x + 2
ƒ (x) = x
Grafica de Funciones lineales
Grafica de Funciones cuadráticas
Graficar ƒ (x) = x2 + 5x + 6 x= -2, -1, 0, 1, 2
ƒ (-2) = (-2)2 + 5(-2) + 6 = 4 – 10 + 6 = 0
ƒ (-1) = (-1)2 + 5(-1) + 6 = 1 – 5 + 6 = 2
ƒ (0) = (0)2 + 5(0) + 6 = 0 + 0 + 6 = 6
ƒ (1) = (1)2 + 5(1) + 6 = 1 + 5 + 6 = 12
ƒ (2) = (2)2 + 5(2) + 6 = 4 + 10 + 6 = 20
ƒ (x) = x2+5x+6

10. Graficar ƒ (x) = x2 x= -2, -1, 0, 1, 2
ƒ (-2) = (-2)2 = 4
ƒ (-1) = (-1)2 = 1
ƒ (0) = (0)2 = 0
ƒ (1) = (1)2 = 1
ƒ (2) = (2)2 = 4
ƒ (x) = x2
Graficar ƒ (x) = x2 +5 x= -2, -1, 0, 1, 2
ƒ (-2) = (-2)2 +5 = 4 +5 = 9
ƒ (-1) = (-1)2 +5 = 1 + 5 = 6
ƒ (0) = (0)2 +5 = 0 +5 = 5
ƒ (1) = (1)2 +5 = 1 +5 = 6
ƒ (2) = (2)2 +5 = 4 +5 = 9 ƒ (x) = x2 +5

11. Grafica de Funciones cúbicas
Graficar ƒ (x) = x3 x= -2, -1, 0, 1, 2
ƒ (-2) = (-2)3 = -8
ƒ (-1) = (-1)3 = -1
ƒ (0) = (0)3 = 0
ƒ (1) = (1)3 = 1
ƒ (2) = (2)3 = 8
ƒ (x) = - x3 x= -2, -1, 0, 1, 2
ƒ (-2) = -(-2)3 = 8
ƒ (-1) = -(-1)3 = 1
ƒ (0) = -(0)3 = 0
ƒ (1) = -(1)3 = -1
ƒ (2) = -(2)3 = -8
ƒ (x) = x3
ƒ (x) = -x3
Gráfica de la funciones trigonométricas
Grafica de la función ƒ (x) = seno (x)
ƒ (x) = sen (x)

12. Grafica de la función ƒ (x) = cos (x)
ƒ (x) = cos (x)
Grafica de la función ƒ (x) = tan (x)
ƒ (x) = tan (x)

13. Características de funciones
Las funciones presentan diferentes características, la s cuales deben ser tipificadas para su posterior análisis. Estas características
dependen de la cardinalidad de los conjuntos de partida y de llegada, así como la relación que existe entre ellos, por lo que las
funciones se clasifican en inyectivas, sobreyectivas, biyectivas, inversible, inversa y compuestas.
Función inyectiva.- La función es inyectiva si a cada elemento del rango es una imagen exclusiva de un único elemento del
dominio.
ƒ
A B
1
3
5
8
a
b
c
Dominio Rango
Las funciones de este tipo son las
lineales, las contantes y las cúbicas.
Función sobreyectiva.- La ƒ es sobreyectiva si los elementos del rango de la función son iguales a los elementos del
conjunto de llegada.
ƒ
A B
a
b
c
1
5
8
Dominio Rango

14. Función biyectiva.- La ƒ es biyectiva si es inyectiva y sobreyectiva a la vez.
ƒ
A B
3
7
4
1
5
8
Dominio Rango
Función inversible.- La ƒ es inversible si y solo si la función es biyectiva.
Función inversa.- Permite invertir el sentido de la correspondencia, tal que a cada elemento del conjunto B se lo
asocia con único elemento del conjunto de partida (A).
Función inversa.- Sean las funciones ƒ : A B g : C D, la función compuesta denotada por ƒ o g es una función que
relaciona A con D.
Función par.- La ƒ es par si la recta a la cual se hace referencia es el y. Si f(x) = f(-x)
f(x) = X2 - 8
f(-x) = (-X)2 – 8 La función es par.
f(-x) = X2 - 8
f(x) = X2
f(-x) = (-X)2 La función es par.
f(-x) = X2

15. Función impar.- La ƒ es impar si el punto al cual se hace referencia es el origen de coordenadas.
Si f(x) = -f(-x) o f(-x) = -f(x)
f(x) = X3
f(-x) = (-X)3
f(-x) = -X3
f(x) = X
f(-x) = (-X)
f(-x) = -X
Función monótona.- Se dice que ƒ es una función monótona en un intervalo I, si y sólo si ƒ es estrictamente creciente
o estrictamente decreciente en ese intervalo.
Si f(x1) > f(x2)
Función creciente.- Una ƒ es creciente en un intervalo I, si y solo sí para cualquier elección de x1 , y x2 en I, siempre
que x1 > x2 , tenemos f(x1) > f(x2).
f(x) = x2 + 5x – 8 si x1 = 5 y x2 = 6
f(5) = 42 y f(6) = 58

16. Función decreciente.- Una ƒ es decreciente en un intervalo I, si y solo sí para cualquier elección de x1 , y x2 en I,
siempre que x1 < x2 , tenemos f(x1) < f(x2).
f(x) = x2 + 5x – 8 si x1 = -5 y x2 = -4
f(-5) = -8 y f(-4) = -12
FUNCIONES EXPONENCIALES
Ejercicio
f(x) = ax a = 2 y x = -2, -1, 0, 1, 2
f(-2) = 2-2 ⟹
1
22 ⟹
1
4
f(-1) = 2-1 ⟹
1
2
f(0) = 20 ⟹ 1
f(1) = 21 ⟹ 2
f(2) = 22 ⟹ 4

17. f(x) = (
1
2
)x a = 2 y x = -2, -1, 0, 1, 2
f(-2) = (
1
2
)-2 ⟹ 22 ⟹ 4
f(-1) = (
1
2
)-1 ⟹ 2
f(0) = (
1
2
) 0 ⟹ 1
f(1) = (
1
2
) 1 ⟹
1
2
f(2) = (
1
2
) 2 ⟹
1
4
FUNCIONES LOGARITMICAS
Es el exponente a la que hay que elevar una base para obtener un número dado.
a.- Jhon Napier ⟶ Logaritmos naturales, base e= 2,7182………… ⟶ In
La función logarítmica (logaritmo natural) se representa con la siguiente notación: f(x)= ln X
N B X
80 푒 4,38
200 푒 5,29
500 푒 6,21
1000 푒 6,9

18. b.- Henrry Briggs ⟶ Logaritmos decimales, base 10 ⟶ log
La función logarítmica (decimal) se representa con la siguiente notación: f(x)= log X
N B X
80 10 1,9
200 200 2,3
500 500 2,69
1000 1000 3
Propiedades de las funciones logarítmicas
NOMBRE EXPRESIÓN
SIMBÓLICA
EQUIVALENCIA EJERCICIOS
Logaritmo de un
producto
log A.B = log A + log
B
La suma de los
logaritmos de cada
factor.
log 21 = log (3)(7)
→ log 3 + log 7
Logaritmo de un
Cociente
퐴
퐵
log(
) = log A – log B
Es la diferencia entre
el log del
numerador y el log
del denominador.
7
3
log (
) = log 7 – log 3
Logaritmo de una
potencia
log (A)n = n log A
Es el exponente por
el logaritmo de la
base.
log 73 = 3 log 7
Logaritmo de una
Raíz enésima
log 푛 퐴 =
log 퐴
푛
Es el cociente entre
el logaritmo de la
base por el
exponente.
log3 11 =
log 11
3

19. Ejercicios
Simplificar usando logaritmo.
An Bc
푛 퐷
1).- log → 푙표푔푎푟푖푡푚표 푑푒 푢푛 푐표푐푖푒푛푡푒
log(An Bc ) − 풍풐품(풏 푫 )
a2 b3
c d2
풏
→ 푙표푔푎푟푖푡푚표 푑푒 푢푛 푝푟표푑푢푐푡표 푦 푙표푔푎푟푖푡푚표 푑푒 푢푛푎 푟푎í푧
log An + log Bc −
풍풐품 푫
풏
→ 푙표푔푎푟푖푡푚표 푑푒 푢푛푎 푝표푡푒푛푐푖푎
R// n log A + c log B −
풍풐품 푫
풏
2).- log
풏 a2 b3
cd2
→ 푙표푔푎푟푖푡푚표 푑푒 푢푛푎 푟푎í푧
log → 푙표푔푎푟푖푡푚표 푑푒 푢푛 푐표푐푖푒푛푡푒 ⟹ a2b3 - log cd2
log → 푙표푔푎푟푖푡푚표 푑푒 푢푛 푝푟표푑푢푐푡표
풏
log a2 + log b3 - log c – log d2
풏
→ 푙표푔푎푟푖푡푚표 푑푒 푢푛푎 푝표푡푒푛푐푖푎
2 log a + 3 log b - log c – 2 log d
풏 R//
Cambio de base
logb N =
log a N
loga B

20. log2 28 = X
N = 28
B = 2
X = ?
Solución
log 1028
log10 2
log2 28 =
log2 28 =
log2 28 =
1,4471
0,3010
4,8076
log5 350 = X
N = 350
B = 5
X = ?
log5 350 =
log5 350 =
log5 350 =
log 10350
log10 5
2,5440
0,6989
3,64
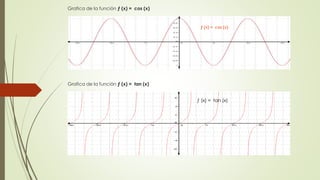
Gráfica de funciones por trozo
Ejercicios
풇 풙 =
풙 + ퟏ ; ퟎ ≥ 풙 > −ퟑ
풙ퟐ; ퟐ ≥ 풙 > ퟎ
풍풐품 풙 ; ퟏퟎ ≥ 풙 > ퟐ
푻풓풂풎풐 풂). 풇 풙 = 풙 + ퟏ ; ퟎ ≥ 풙 > −ퟑ 풙 = (−3 , 0 ]
푻풓풂풎풐 풃). 풇 풙 = 풙ퟐ ; ퟐ ≥ 풙 > ퟎ 풙 = (1 , 2 ]
풇 ퟏ = ퟏퟐ = 1
풇 ퟐ = ퟐퟐ = ퟒ
풇 −ퟑ = −ퟑ + ퟏ = −ퟐ
풇 −ퟐ = −ퟐ + ퟏ = −ퟏ
풇 −ퟏ = −ퟏ + ퟏ = ퟎ
풇 ퟎ = ퟎ + ퟏ = ퟏ 푻풓풂풎풐 풄). 풇 풙 = 풍풐품 풙 ; ퟏퟎ ≥ 풙 > ퟐ 풙 = (2 , 10 ]
풇 ퟐ = 풍풐품 ퟐ = 0,30
풇 ퟒ = 풍풐품 ퟒ = ퟎ, ퟔퟎ

21. 풇 ퟔ = 풍풐품 ퟔ = 0,77
풇 ퟖ = 풍풐품 ퟖ = ퟎ, ퟗퟎ
풇 ퟏퟎ = 풍풐품 ퟏퟎ = ퟏ
Representación gráfica
풇 풙 =
풙 + ퟏ ; ퟎ ≥ 풙 > −ퟑ
풙ퟐ; ퟐ ≥ 풙 > ퟎ
풍풐품 풙 ; ퟏퟎ ≥ 풙 > ퟐ
g 풙 =
풙 + ퟏ ; 풙 ≤ −ퟏ
풙 ; 풙 < ퟏ
풙ퟐ + ퟏ ; ퟏ ≤ 풙 ≤ ퟑ
ퟒ ; 풙 > ퟒ
Solución
푻풓풂풎풐 풂). 품 풙 = 풙 + ퟏ ; 풙 ≤ −ퟏ 풙 = [−1, −∞)
풇 −ퟏ = −ퟏ + ퟏ = −0
풇 −ퟐ = −ퟑ + ퟏ = −ퟐ
풇 −ퟓ = −ퟓ + ퟏ = −ퟒ
풇 −ퟔ = −ퟔ + ퟏ = −ퟓ
푻풓풂풎풐 풂). 품 풙 = 풙 ; 풙 < ퟏ 풙 = −∞, −1 ∪ (1, ∞)
풇 −ퟓ = −ퟓ + ퟏ = −4
풇 −ퟑ = −ퟑ + ퟏ = −ퟐ
풇 −ퟏ = −ퟏ + ퟏ = −ퟎ
풇 ퟏ = ퟏ + ퟏ = ퟐ
풇 ퟑ = ퟑ + ퟏ = ퟒ
풇 ퟓ = ퟓ + ퟏ = ퟔ

22. 푻풓풂풎풐 풄). 품 풙 = 풙ퟐ + ퟏ ; ퟏ ≤ 풙 ≤ ퟑ 풙 = [ퟏ, ퟑ]
풇 ퟏ = ퟏퟐ +ퟏ = ퟏ + ퟏ = 2
풇 ퟐ = ퟐퟐ + ퟏ = ퟒ + ퟏ = ퟓ
풇 ퟑ = ퟑퟐ + ퟏ = ퟗ + ퟏ = ퟏퟎ
푻풓풂풎풐 풅). 품 풙 = ퟒ ; 풙 > ퟒ 풙 = (ퟒ, ∞)
풇 ퟒ = 4
풇 ퟓ = ퟓ
풇 ퟔ = ퟔ
풇 ퟕ = ퟕ
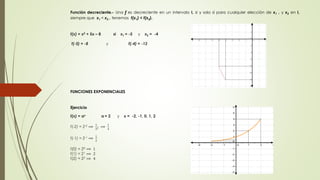
Representación gráfica
g 풙 =
풙 + ퟏ ; 풙 ≤ −ퟏ
풙 ; 풙 < ퟏ
풙ퟐ + ퟏ ; ퟏ ≤ 풙 ≤ ퟑ
ퟒ ; 풙 > ퟒ

23. Operaciones con funciones
Adición y sustracción
풇 풙 + 품 풙 = 푥2 + 5푥 − 8 + (3 − 4푥 + 5푥2)
= 6풙ퟐ + x - 5
Ejercicios en clase
푓 −2 = (−2)2+5 −2 − 8 = 4 − 10 − 8 = −14
푓 −1 = (−1)2+5 −1 − 8 = 1 − 5 − 8 = −12
푓 0 = (0)2 +5 0 − 8 = 0 + 0 − 8 = − 8
푓 1 = (1)2 +5 1 − 8 = 1 + 5 − 8 = −2
푓 2 = (2)2 +5 2 − 8 = 4 + 10 − 8 = 6
푔 −2 = 3 − 4 −2 + 5(−2)2 = 3 + 8 − 20 = 31
푔 −1 = 3 − 4 −1 + 5(−1)2 = 3 + 4 + 5 = 12
푔 0 = 3 − 4 0 + 5(0)2 = 3 − 0 + 0 = 3
푔 1 = 3 − 4 1 + 5(1)2 = 3 − 4 + 5 = 4
푔 2 = 3 − 4 2 + 5(2)2 = 3 − 8 + 10 = 6
푅 −2 = 6(−2)2 + −2 − 5 = 24 − 2 − 5 = 17
푅 −1 = 6(−1)2 + −1 − 5 = 6 − 1 − 5 = 0
푅 0 = 6(0)2 + 0 − 5 = 0 + 0 − 5 = −5
푅 1 = 6(1)2 + 1 − 5 = 6 + 1 − 5 = 2
푅 2 = 6(2)2 + 2 − 5 = 24 + 2 − 5 = 21
1)
2) ퟏ
풇 풙 = ퟏ
풙ퟐ + 풙
풙ퟐ − 풙
품 풙 =
Hallar
a) 풇 풙 + 품 풙
ퟏ
R(x) = + = + = = =
풙ퟐ + 풙
1
푥2 − 푥
1
푥(푥 + 1)
1
푥(푥 − 1)
푥2 − 푥 + 푥2 + 푥
푥(푥 − 1)(푥 + 1)
2푥2
푥(푥 − 1)(푥 + 1)
2푥
푥2 − 1
Si 풇 풙 = 풙ퟐ + ퟓ풙 − ퟖ y g 풙 = ퟑ − ퟒ풙 + ퟓ풙ퟐ ; 2 ≥ x ≥ -2

24. b) ퟐ풇 풙
2
ퟏ
풙ퟐ+풙
1
R(x) = = 2 =
푥(푥 + 1)
2
푥(푥 + 1)
c) 품 풙 − 풇 풙
1
R(x) = - = - = = =
푥2 − 푥
1
푥2 + 푥
푥2 + 푥 − 푥2 + 푥
푥(푥 + 1)(푥 − 1)
2푥
푥(푥 − 1)(푥 + 1)
1
푥(푥 − 1)
1
푥(푥 + 1)
2
푥2 − 1
d) 풇 풙 − 품 풙
1
R(x) = - = - = = =
푥2 + 푥
1
푥2 − 푥
1
푥(푥 + 1)
1
푥(푥 − 1)
푥2 − 푥 − 푥2 − 푥
푥(푥 + 1)(푥 − 1)
−2푥
푥(푥 − 1)(푥 + 1)
−2
푥2 − 1
e) 3품 풙
1
1
푥2−푥
R(x) = = 3 =
푥(푥 − 1) 3
3
푥(푥 − 1)
f) ퟐ풇 풙 + ퟑ품 풙
2
R(x) = + = = =
푥(푥 + 1)
3
푥(푥 − 1)
2 푥 − 1 + 3(푥 + 1)
푥(푥 − 1)(푥 + 1)
2푥 − 2 + 3푥 + 3
푥(푥 − 1)(푥 + 1)
5푥 + 1
푥(푥 − 1)(푥 + 1)
Multiplicación y División
3) Si 풇 풙 = 풙 + ퟓ y 품 풙 = 풙 − ퟖ
풇 풙 . 품 풙 = 푥 + 5 . (푥 − 8)
= 풙ퟐ -3x -40

25. 4)
풇 풙 =
Hallar
푥2 + 5푥 + 6
푥2 − 1
품 풙 =
푥2 − 2푥 + 1
푥2 − 4
a) 풇 풙 ∗ 품 풙
풙ퟐ+ퟓ풙+ퟔ
풙ퟐ−ퟏ
∗
풙ퟐ−ퟐ풙+ퟏ
풙ퟐ−ퟒ
=
(풙+ퟑ)(풙+ퟐ)
(풙+ퟏ)(풙−ퟏ)
∗
푥−1 푥−1
푥+2 푥−2
=
(푥+3)(푥−1)
(푥+1)(푥−2)
풇 풙 ÷ 품 풙
풙ퟐ+ퟓ풙+ퟔ
풙ퟐ−ퟏ
÷
풙ퟐ−ퟐ풙+ퟏ
풙ퟐ−ퟒ
=
(풙+ퟑ)(풙+ퟐ)
(풙+ퟏ)(풙−ퟏ)
∗
푥+2 푥−2
푥−1 푥−1
=
푥+3 푥−1 푥−2 푥+2
푥+1 푥−1 푥−1 푥−1
∗
푥−2 2 푥+3 푥−1
풙ퟐ−1 푥−1 2
b)
Composición de funciones
Si 풇 풙 = 풙ퟐ + ퟓ풙 − ퟑ 품 풙 = 풙 + ퟖ
(풇 풐 품)(x)
풇 풙 + ퟏ (풇 풐 품)(x) = (x+1)2 + 5(x+1) - 3
= x2 + 2x + 1 + 5x + 5 - 3
= x2 + 7x + 3
풇 풙2 + ퟓ풙 − ퟑ (품 풐 풇)(x) = (x2 + 5x – 3) + 1
= x2 + 5x – 3 + 1
= x2 + 5x - 2
Dada la función 풇 풙 = 풙ퟐ + ퟐ풙 + ퟑ y 품 풙 = 풙 − ퟓ

26. (풇 풐 품)(1) = 풇(품(1))
푓(푔(1)) = 푓(1 − 5)
푓(푔(1)) = 푓(−4)
푓 −4 = 푥2 + 2푥 + 3
푓 −4 = (−4)2+2 −4 + 3
푓(−4) = 16 – 8 + 3
푓(−4) = 11
(품 풐 풇)(1) = g(풇(1))
푔(푓(1)) = 푓 1 2 + 2 1 + 3
푔(푓(1)) = 푓 1 + 2 + 3
푔(푓(1)) = 푓 6
푔 6 = 푥 − 5
푔 6 = 6 − 5
푔 6 = 1
(품 풐 풇)(−3) = g(풇(−3))
푔(푓(−3)) = 푓 −3 2 + 2 −3 + 3
푔(푓(−3)) = 푓 9 − 6 + 3
푔(푓(−3)) = 푓(6)
푔 6 = 푥 − 5
푔 6 = 6 − 5
푔 6 = 1
(풇 풐 품)(−3) = 풇(품(−3))
푓(푔(−3)) = 푓(−3 − 5)
푓(푔(−3)) = 푓(−8)
푓 −8 = 푥2 + 2푥 + 3
푓 −8 = (−8)2+2 −8 + 3
푓(−8) = 64 – 16 + 3
푓(−8) = 51

27. LIMITE
Limite es una constante, a la cual la variable se aproxima.
Ejemplo
Limite de una variable
1) Si la variable pasa de: 2,8 ; 2,9 ; 2,95 ; 2,98 estamos en condición de decir que su límite es : 3 ⟹ 풍풊풎 ퟑ ⟶ limite
superior.
2) Si la variable dentro de su proceso obtiene valores de: 2,2 ; 2,1 ; 2,08 ; 2,05 su límite es: 2 ⟹ 풍풊풎 ퟐ ⟶ limite inferior.
Limite de una función
풇 풙 = 풙ퟐ − 풙 + ퟐ
푓 푥 = (2,8)2−2,8 + 2
푓 푥 = 7,84 − 2,8 + 2
푓 푥 = 7,08 ∴ 푙푖푚 푓 푥 = 8
Observando el desarrollo podemos decir que el límite de una función 풇 풙 es igual a 8.
Por lo tanto podemos también definir que el límite de una función es una constante cuando la variable también se
aproxima a la constante.
Sea 풇 풙 = 풙ퟐ − 풙 + ퟐ
풇 풙 Y
2,8
2,9
2,95
2,98
7,08
7,51
7,75
7,9
푙푖푚
푥⟶푎
풙ퟐ − 풙 + ퟐ
푓 푥 = 퐴
ퟑ
ퟖ

28. 풇 풙 = 풙ퟐ + 풙 − ퟑ
lim
푥→2
푓 푥 = 푥2 + 푥 − 3
푓 푥 = 22 + 2(2) − 3
푓 푥 = 4 + 4 − 3
푓 푥 = 5 ∴ 푙푖푚 푓 푥 = 5
Ejercicios en clase
2) Hallar 풍풊풎
풙→−ퟑ
풙ퟐ −ퟓ풙 + ퟗ
풙 − ퟏ
(풙ퟐ − ퟓ풙 + 8 )
푙푖푚
푥→−2
= (−2)2−5(−2) + 8 = 4 + 10 +8 = 22
1) Hallar el límite de 풍풊풎
풙→−ퟐ
풍풊풎
풙→−ퟑ
(−ퟑ)ퟐ −ퟓ(−ퟑ) + ퟗ
−ퟑ− ퟏ
=
ퟗ + ퟏퟓ + ퟗ
−ퟑ− ퟏ
= −
ퟑퟑ
ퟒ
Propiedades que se cumplen en los límites
1.- Límite de una suma algebraica.
lim
푥→푎
퐴 + 퐵 + 퐶 = lim
푥→푎
(퐴) + lim
푥→푎
퐵 + lim
푥→푎
(퐶)
lim
푥→2
3푥 + 5풙ퟐ − 8 = lim
푥→2
(3푥) + lim
푥→2
5풙ퟐ − lim
푥→2
(8)
Ejemplo
lim
푥→2
3푥 + 5풙ퟐ − 8 = 3(2) + 5(ퟐ)ퟐ− 8
= 6 + 20 – 8
= 18
2.- Límite de un producto por una constante.
lim
푥→푎
퐶 푥 = 퐶 lim
푥→푎
푥
3.- Límite de una constante.
lim
푥→푎
푏 = 푏
4.- Límite de un producto.
lim
푥→푎
푢. 푣 = lim
푥→푎
푢 lim
푥→푎
푣
lim
푥→1
푥 + 2)(푥 − 8 = lim
푥→1
5.- Límite de un cociente.
푥 + lim
푥→1
2 lim
푥→1
푥 − lim
푥→1
8
= (1 + 2) (1 – 8)
= (3)(-7)
= - 21
Ejemplo
lim
푥→푎
푢
푣
=
lim
푥→푎
(푢)
lim
푥→푎
(푣)

29. Nota.-Cuando el resultado de una es
0
0
, no esta determinada, por lo que debemos factorizar antes de aplicar límite.
Cuando el resultado es
∞
∞
, después de la solución directa. Debemos dividir todos los términos para la variable
con mayor exponente.
Ejercicios
ퟐ풙ퟑ − ퟑ풙ퟐ + ퟒ
1) 풍풊풎
푙푖푚
풙→∞
ퟓ풙 − 풙ퟐ − ퟕ풙 ퟑ 푥→∞
2푥3
푥3 −
3푥2
푥3 +
4
푥3
5푥
푥3 −
푥2
푥3 −
7푥3
푥3
푙푖푚
푥→∞
2 −
3
푥
+
4
푥3
5
푥2 −
1
푥
− 7
=
2−
3
∞
+
4
∞
5
∞
−
1
∞
− 7
= -
2
7
ퟓ − ퟐ풙ퟐ
2) 풍풊풎
푙푖푚
풙→∞
ퟑ풙 − ퟓ풙ퟐ 푥→∞
5
푥2 −
2푥2
푥2
3푥
푥2 −
5푥2
푥2
푙푖푚
푥→∞
5
2 − 2
푥3
+ 5
푥
푙푖푚
푥→∞
4 +
5
∞
2 +
3
∞
= -
2
5
풍풊풎
풙→∞
ퟒ풙 + ퟓ
ퟐ풙 + ퟑ
3)
푙푖푚
푥→∞
4푥
푥
+
5
푥
2푥
푥
+
3
푥
=
5
∞
− 2
3
∞
+ 5
=
4
2
= 2

30. 풍풊풎
풙→ퟎ
ퟒ풕ퟐ −ퟑ풕+ퟐ
풕ퟑ+ퟐ풕−ퟔ
= −
ퟏ
ퟑ
5)
4(0)2 − 3(0) + 2
(0)3+2(0) − 6
= −
2
6
= −
1
3
풍풊풎
풙→풂
푺ퟒ − 풂ퟒ
푺ퟐ − 풂ퟐ = 2푎2
4)
푙푖푚
푥→푎
(푺ퟐ+ 풂ퟐ)(푺ퟐ − 풂ퟐ)
푺ퟐ − 풂ퟐ
푙푖푚
푥→푎
(푆2+ 푎2) = 푎2 + 푎2 = 2푎2
풍풊풎
풉→ퟎ
풙+풉 − 풙
풉
= −
ퟏ
ퟐ 풙
푙푖푚
푥→0
푥 + ℎ − 푥
ℎ
∗
푥 + ℎ + 푥
푥 + ℎ + 푥
푙푖푚
푥→0
( 푥 + ℎ)2 − ( 푥)2
ℎ 푥 + ℎ + 푥
푙푖푚
푥→0
푥 + ℎ − 푥
ℎ 푥 + ℎ + 푥
푙푖푚
푥→0
1
푥 + ℎ + 푥
1
푥 + 0 + 푥
=
1
푥+ 푥
=
1
2 푥
7)
Dado 푓 푥 =
1
풙ퟐ 1
푥
demostrar que 풍풊풎
풉→ퟎ
풇(풙+풉) −풇(풙)
풉
= −
6) Demostrar que:
푓 푥 =
1
푥
푓 푥 + ℎ =
1
푥+ℎ
푙푖푚
푥→0
1
푥 + ℎ
−
1
푥
ℎ
푙푖푚
푥→0
푥 − 푥 + ℎ
푥(푥 + ℎ)
ℎ
푙푖푚
푥→0
−ℎ
풙ퟐ + 푥ℎ
ℎ
푙푖푚
푥→0
−1
풙ퟐ + 푥ℎ
=
−1
풙ퟐ + 푥(0)
= −
1
풙ퟐ

31. ¿Qué es derivada?
DERIVADAS
La derivada de una función es una razón de cambio instantánea, según cambie el valor de su variable
independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez
de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable
independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en
un punto dado.
¿Cuál es la notación de la deriva ?
La derivada se denota con la siguiente notación:
푑푦
푑푥
→ derivada de y con respecto a x.
¿ Qué se deriva ?
Se deriva funciones utilizando el método de incremento.
¿Qué es un incremento ?
Un incremento es una variación infinitesimal del valor de una variable que se usa para definir determinados
conceptos analíticos. El incremento se representa con el siguiente símbolo: Δ.
풙Δ = x1 + x2 ∴ x2 = x1 + 풙Δ
푓푢푡푢푟푎
A푐푡푢푎푙
Ejemplo
y = 풙ퟐ + ퟑ풙 Damos incremento a la variable independiente (x).
y +Δy = (x1 + Δ풙)ퟐ + ퟑ(x1 + Δ풙)

32. Desarrollamos las operaciones algebraicas.
y +Δy = x2 + 2x1Δx + (Δx)2 +3x1 + 3Δx
Despejamos Δy .
Δy = x2 + 2x1Δx + (Δx)2 +3x1 + 3Δx − y
Reemplazamos y‘ por su equivalente.
Δy = x2 + 2x1Δx + (Δx)2 +3x1 + 3Δx − x1
Reducimos términos semejantes.
2 +3x1
Δy = 2x1Δx + (Δx)2 + 3Δx
Razón de incremento →
Δ푦
Δ푥
Δ푦
Δ푥
=
2x1Δ푥
Δ푥
+
(Δx)2
Δ푥
+
3Δ푥
Δ푥
Δ푦
Δ푥
= 2x1 + Δ푥 + 3
Aplicamos límite a cada miembro de la ecuación.
lim
Δ푥→0
Δ푦
Δ푥
= lim
2x1 + lim
Δ푥→0
Δ푥→0
Δ푥 + lim
3
Δ푥→0
= 2x1 + 0 + 3
= 2x1 + 3
Desarrollo de derivadas por incremento.
1). 풇 풙 = 풙ퟑ − ퟐ풙ퟐ + ퟓ풙 − ퟖ Hallar la derivada por incremento.
y +Δy = (x + Δ푥)3 − 2 x + Δ푥 2 +5 x + Δ푥 − 8
y +Δy = x3 + 3푥2Δ푥 + 3푥(Δ푥)2 + (Δ푥)3−2푥2 − 4푥Δ푥 − 2 Δ푥 2 + 5푥 + 5Δ푥 − 8
Δy = x3 + 3푥2Δ푥 + 3푥(Δ푥)2 + (Δ푥)3−2푥2 − 4푥Δ푥 − 2 Δ푥 2 + 5푥 + 5Δ푥 − 8
Δ − x3 +3푥2Δ푥 + 3푥(Δ푥) + (Δ푥)3+2푥2 − 4푥Δ푥 − 2 Δ푥 2 − 5푥 + 5Δ + 8
Δy = 3푥2Δ푥 + 3푥(Δ푥)2 + (Δ푥)3−4푥Δ푥 − 2 Δ푥 2 + 5Δ푥
Δ푦
Δ푥
=
3푥2Δ푥
Δ푥
+
3푥(Δ푥)2
Δ푥
+
(Δ푥)3
Δ푥
−
4푥Δ푥
Δ푥
−
2 Δ푥 2
Δ푥
+
5Δ푥
Δ푥
Δ푦
Δ푥
= 3푥2 + 3푥Δ푥 +(Δ푥)2 −4푥 − 2Δ푥 + 5
lim
Δ푥→0
Δ푦
Δ푥
= lim
(3푥2 + 3푥Δ푥 +(Δ푥)2 −4푥 − 2Δ푥 + 5)
Δ푥→0
lim
Δ푦
Δ푥
= 3푥2 − 4푥 + 5
2). 풇 풙 =
ퟏ
풙
Hallar la derivada.
y +Δy =
1
푥 + Δ푥
Δy =
1
푥 + Δ푥
− y
Δy =
1
푥 + Δ푥
−
1
푥

33. Δy =
푥 − 푥 − Δ푥
푥(푥 + Δ푥)
Δ푦
Δ푥
=
−Δ푥
푥(푥 + Δ푥)
Δ푥
= −
1
푥(푥 + Δ푥)
Δy =
−Δ푥
푥(푥 + Δ푥)
lim
Δ푥→0
Δ푦
Δ푥
= lim
Δ푥→0
−
1
푥 푥 + Δ푥
lim
Δ푦
Δ푥
= −
1
푥2
3). 풇 풙 =
풙+ퟏ
풙−ퟏ
Hallar la derivada.
y +Δy =
푥 + Δ푥 + 1
( 푥 + Δ푥) − 1
Δy =
푥 + Δ푥 + 1
( 푥 + Δ푥) − 1
−
푥 + 1
푥 − 1
Δy =
푥 − 1 푥 + Δ푥 + 1 − 푥 + 1 푥 + Δ푥 − 1
푥 − 1 푥 + Δ푥 − 1
Δy =
푥2 + 푥Δ푥 − 1 − 푥2 −푥Δ푥 − Δ푥 + 1
푥 − 1 푥 + Δ푥 − 1
Δy =
−2Δ푥
푥 − 1 푥 + Δ푥 − 1
Δ푦
Δ푥
=
−2Δ푥
푥 − 1 푥 + Δ푥 − 1
Δ푥
= −
2
푥 − 1 푥 + Δ푥 − 1
lim
Δ푥→0
Δ푦
Δ푥
= lim
Δ푥→0
−
2
푥2−2푥 − Δ푥 + Δ푥 + 1
lim
Δ푥→0
−
2
푥2−2푥 + 1
lim
Δ푦
Δ푥
= −
2
푥2 −2푥 + 1
4). 푺 = ퟐ풕 − 풕ퟐ Hallar la derivada.
S +ΔS = ퟐ(t + Δt) − (t + Δ풕)ퟐ
S +ΔS = ퟐt + 2Δt − 풕ퟐ − 2tΔ풕 − (Δ풕)ퟐ
ΔS = ퟐt + 2Δt − 풕ퟐ − 2tΔ풕 − (Δ풕)ퟐ
S +ΔS − ퟐt + 2Δt + 풕ퟐ − 2tΔ풕 − Δ풕ퟐ
ΔS = 2Δt − 2tΔ풕 − (Δ풕)ퟐ
Δ푆
Δ푡
=
2Δt
Δ푡
−
2tΔ풕
Δ푡
−
(Δ풕)ퟐ
Δ푡
Δ푆
Δ푡
= 2 − 2푡 − Δ푡
lim
Δ푡→0
Δ푆
Δ푡
= lim
Δ푡→0
(2 − 2푡 − Δ푡)
lim
Δ푦
Δ푥
= 2 − 2푡

34. Reglas para derivar funciones.
NOMBRE EXPRESIONES ALGEBRAICA EQUIVALENCIA EJEMPLOS
Derivada de una conste 푑(푐)
푑푥
= 0 A cero 푑(5)
푑푥
= 0
Derivada de una variable con
respecto a sí mismo
푑푥
푑푥
= 1 A uno 푑(푡)
푑푡
= 1
Derivada de una potencia 푑(푣푛)
푑푥
= 푛 ∗ 푣푛−1 ∗
푑(푣)
푑푥
Al producto entre el exponente
por la potencia con exponente
menos uno, por la derivada de
la base.
푑(푥5 )
푑푥
= 5 ∗ 푥5−1 ∗
푑 푥
푑푥
= 5푥4
Derivada de una suma algebraica
푑(푢 + 푣 + 푤)
푑푥
=
푑(푢)
푑푥
+
푑(푣)
푑푥
−
푑(푤)
푑푥
La suma algebraica de las
derivadas
푑(푥2 + 3푥 − 1)
푑푥
=
푑(푥2)
푑푥
+
푑(3푥)
푑푥
−
푑(1)
푑푥
Derivada de un producto entre una
constante y una variable
푑(푐. 푣)
푑푥
= 푐 ∗
푑(푣)
푑푥
Al producto entre la constante
y la derivada de la variable
푑(5푥)
푑푥
= 5 ∗
푑 푥
푑푥
= 5
Derivada de un producto
푑(푢. 푣)
푑푥
= 푢 ∗
푑 푣
푑푥
+ 푣 ∗
푑 푢
푑푥
A la derivada del primer factor
por la derivada del segundo
factor más el segundo factor
por la derivada del primero
Derivada de un cociente
푑
푢
푣
푑푥
=
푣.
푑(푢)
푑푥
− 푢.
푑(푣)
푑푥
푣2
El denominador por la derivada
del numerador menos el
numerador por la derivada del
denominador sobre el
denominador al cuadrado

35. Ejercicios
1)
[3(x-1)2] (x-1)2
푑
푑푥
= 3
푑
푑푥
= 3 2 *
(푥 −1)
푑
푑푥
= 6(푥 − 1) *
푑(푥)
푑푥
−
푑(1)
푑푥
= 6(푥 − 1)
2)
푑(푥−4)
푑푥
= −4 ∗ 푥−5 푑(푥)
푑푥
= −4푥−5
3)
(8푥−
푑
푑푥
3
4)
= 8 ∗
(푥−
푑
푑푥
3
4)
4 ∗ 푥−
= 8 ∗ −3
7
3 ∗
푑(푥)
푑푥
3 푥−
= −32
7
3
=
(푥2 + 1)1
푑
푑푥
2
4)
푑
푑푥
( 푥2 − 1)
2 ∗ (푥2 + 1)−1
= 1
2
푑 푥2
푑푥
−
푑(1)
푑푥
2 ∗ (푥2 + 1)−1
= 1
2 ∗ 2푥
= 푥(푥2 + 1)− 1
2
=
푥
푥2−1
5)
푑
푑푥
[풙
ퟏ
ퟐ(풙ퟐ + ퟓ)]
푥
1
2 ∗
푑
푑푥
푥2 + 5 + 푥2 + 5
1
2
푑푥
푑 푥
푥
1
2
푑(푥2)
푑푥
+
푑(5)
푑푥
+ 푥2 + 5
1
2
1
2 ∗
∗ 푥−
푑(푥)
푑푥
푥
1
2 ∗ 2푥 ∗
푑푥
푑푥
+ 푥2 + 5
1
2푥
1
2
2푥
3
2 +
푥2 + 5
2푥
1
2
4푥2 + 푥2 + 5
2푥
1
2
=
5푥2+5
2푥
1
2
=
5(푥2+1)
2 푥
6)
풙 + ퟏ
풙 − ퟏ =
풅
풅풙
푥 − 1
푑
푑푥
푥2 + 1 푥2 − 1
− 푥 + 1
푑
푑푥
(푥 − 1)2
=
푥 − 1 (1) − 푥 + 1 (1)
(푥 − 1)2
=
푥 − 1 − 푥 − 1
(푥 − 1)2
= −
1
(푥 − 1)2

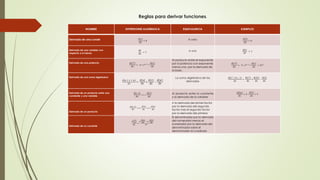
36. Aplicación de la derivada en el mundo
empresarial
Ejercicios
1) y = (풙ퟐ − 풙)ퟑ ; 풙 = ퟑ
y = 3(푥2 − 푥)2 풅
풅풙
(풙ퟐ − 풙)
(푥2 − 5)1
2
y = 3 푥2 − 푥 2 (2푥 − 1)
y = 3 푥2 − 푥 2 (2푥 − 1)
Si 푥 = 3 → 푦′ = ?
y = 3 32 − 3 2 (2 ∗ 3 − 1)
y = 3 6 2 (5)
y = 540
2) y =
풙ퟐ−ퟓ
ퟏퟎ−풙ퟐ ; 풙 = ퟑ
y =
(푥2−5) 1
2
(10−푥2) 1
2
1
2 ∗
(풙ퟐ − ퟓ) (ퟏퟎ − 풙ퟐ )
y =
1
2
(10−푥2)
푑
푑푥
−(푥2−5) 1
2
푑
푑푥
[10−푥2) 1
2]2
(10 − 푥2) 1
2
y =
1
2∗
(10−푥2)
1
2
−
(푥2−5)
1
2
푑
푑푥
− (푥2−5)
1
2
−
(10−푥2)
1
2
푑
푑푥
(10−푥2)2
y =
1
2 ∗2푥
(10−푥2)
1
2
2(푥2−5)
−
1
2 ∗(−2푥)
(푥2−5)
1
2
2(10−푥2)
(10−푥2)2
y =
푥 10−푥2 +푥 푥2−5
1
2(10−푥2)
(10−푥2) (푥2−5)
1
2
y =
10푥−푥3+푥3−5푥
1
2(10−푥2)
(10−푥2) (푥2−5)
1
2
y =
5푥
1
2(10−푥2)
(10−푥2) (푥2−5)
1
2
y =
5(3)
1
2(10−32)
(10−32) (32−5)
1
2
Si 푥 = 3 → 푦′ = ?
y =
15
1
2(10−9)
(10−9)(9 −5)
1
2
y =
15
1
2(1)
(1)(4)
1
2
y =
15
(1)(2) (1)
y =
15
2
3) y = ퟑ 풙 + 풙; 풙 = ퟔퟒ
y = 푥
1
3+ 푥
1
2
y = 2
3
(푥−
1
3)
푑(푥)
푑푥
+
2
3
푥−
1
2
푑(푥)
푑푥
y =
1
3
3
푥2
+
1
2 푥
y =
1
3
3
642
+
1
2 64

37. y =
1
3
3
642
+
1
2 64
y =
1
3
3
[(4)3]2 +
1
2 64
y =
1
3∗16
+
1
2∗8
y =
1
3∗16
+
1
16
y =
1+3
3∗16
=
4
3∗16
=
1
3∗4
=
1
12
Hallar la pendiente de cada una de las siguientes
curvas en el punto dado:
4) 풙ퟐ + 풙풚 + ퟐ풚ퟐ = ퟐퟖ ; 풑(ퟐ, ퟑ)
(푥2+푥푦 + 2푦2) (28)
푑
푑푥
=
푑
푑푥
푑
푑푥
+
푑
푑푥
+
푑
푑푥
= 0
(푥2) (푥푦) (2푦2)
2푥
푑푥
푑푥
+ 푥
푑푦
푑푥
+ 2
푑
푑푥
= 0
(푦2)
2푥 + 푥
푑푦
푑푥
+ 푦 + 2 ∗ 2푦
푑푦
푑푥
= 0
2푥 + 푥
푑푦
푑푥
+ 푦 + 4푦
푑푦
푑푥
= 0
푥
푑푦
푑푥
+ 4푦
푑푦
푑푥
= −2푥 − 푦
푑푦
푑푥
(푥 + 4푦) = −(2푥 + 푦)
푑푦
푑푥
= −
2푥 + 푦
푥 + 4푦
푑푦
푑푥
= −
2 ∗ 2 + 3
2 + 4 ∗ 3
= −
7
14
= −
1
2