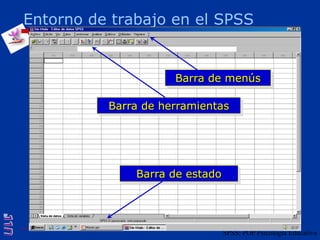
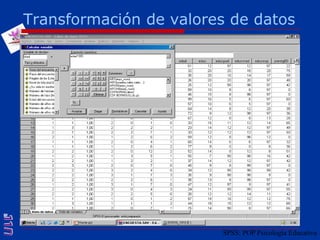
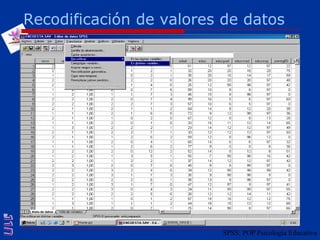
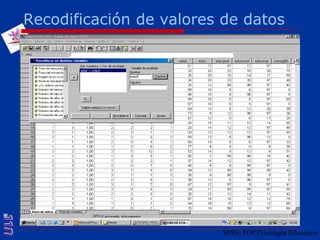
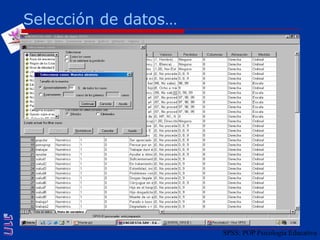
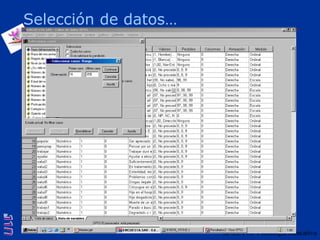
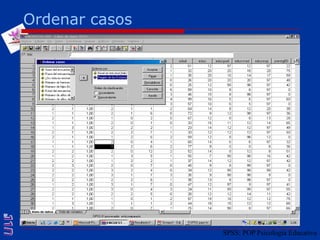
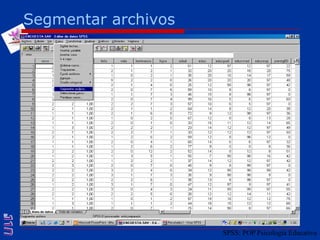
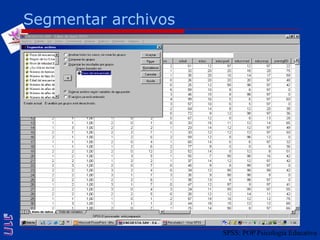
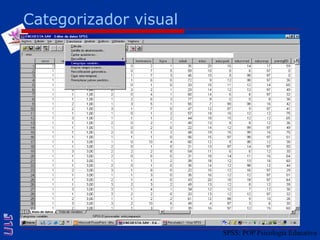
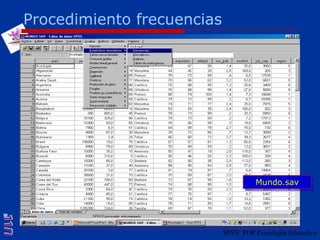
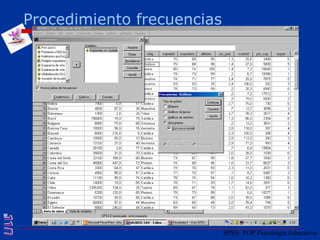
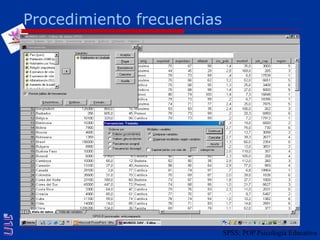
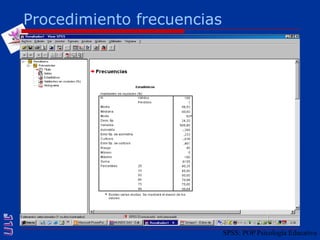
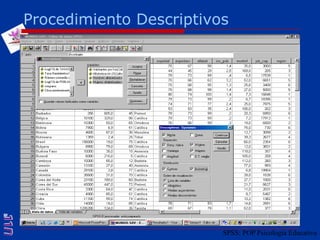
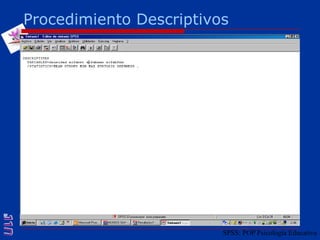
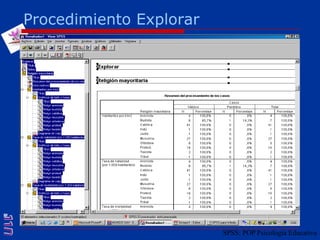
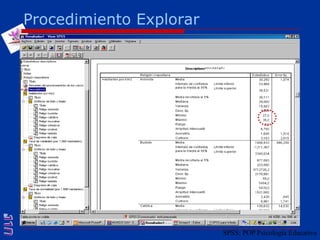
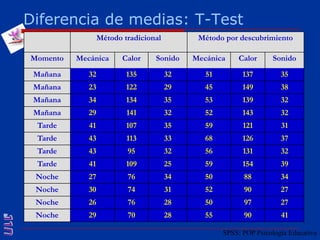
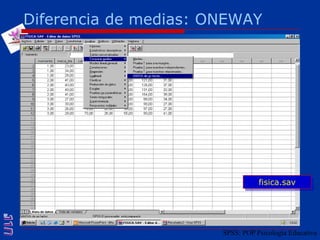
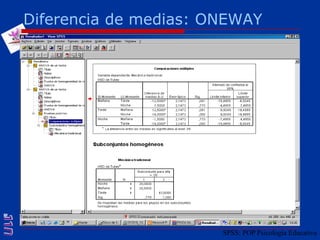
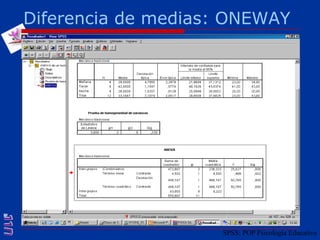
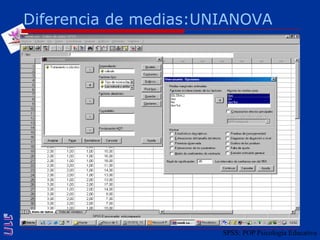
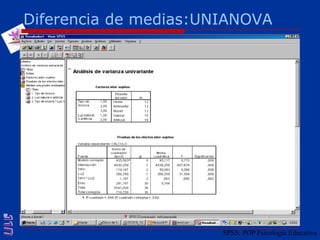
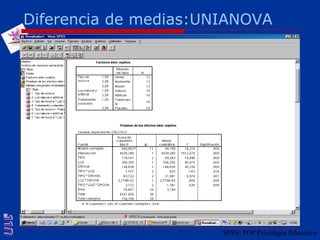
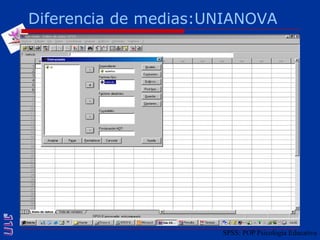
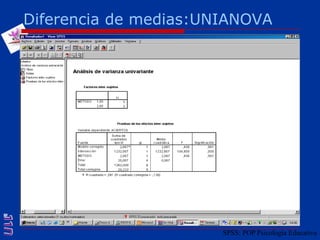
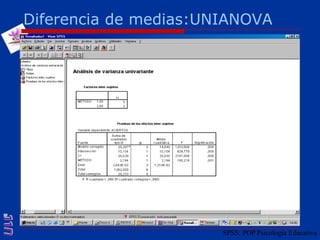
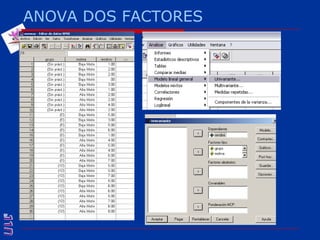
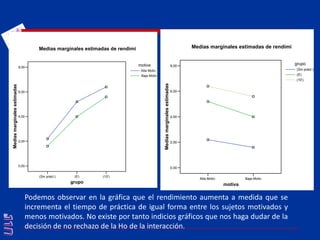
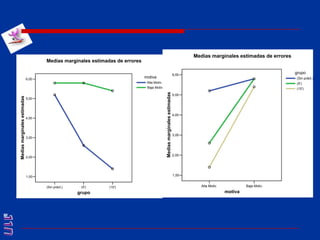
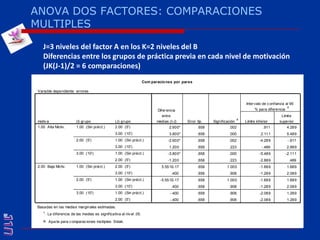
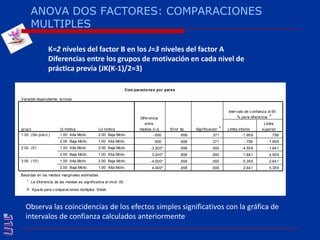
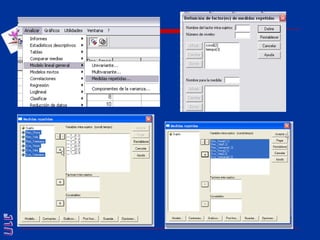
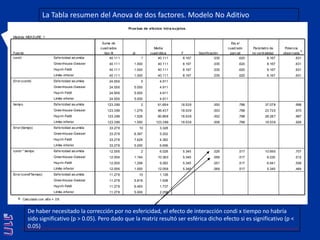
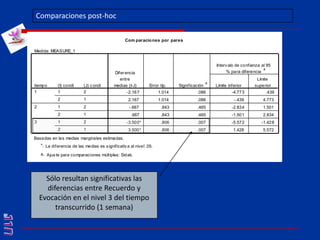
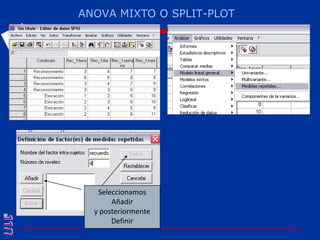
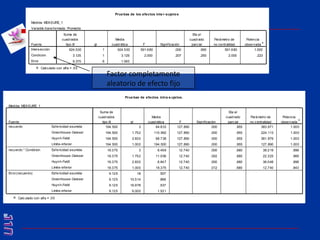
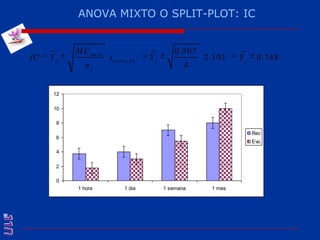
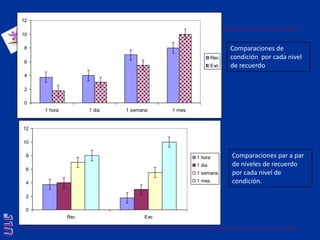
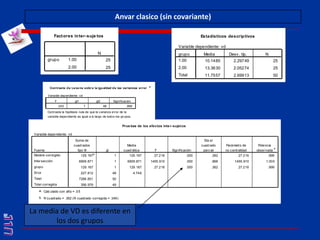
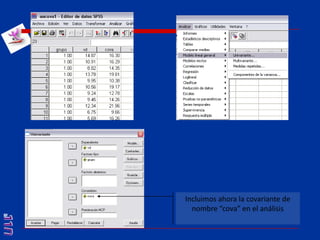
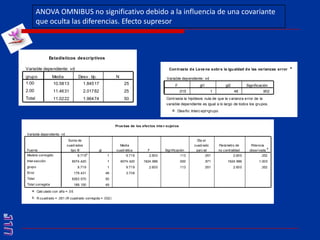
El documento presenta una introducción al uso del software SPSS para el análisis de datos en psicología, abarcando aspectos como la creación y transformación de datos, la estadística descriptiva, y diversas pruebas estadísticas como ANOVA y ANCOVA. Se detallan las funcionalidades del entorno de trabajo, incluyendo el editor de datos, gráficos y resultados, además de los procedimientos para analizar diferencias de medias y varianzas. Se enfatiza la importancia de verificar supuestos estadísticos y analizar interacciones entre variables en investigaciones psicológicas.