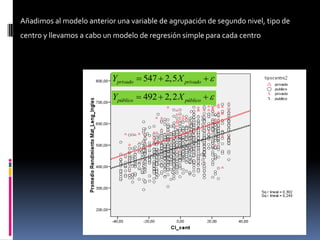
1. El documento describe los modelos multinivel y cómo manejar la dependencia de datos cuando la estructura jerárquica afecta los datos del primer nivel. 2. Explica que los modelos multinivel permiten estimar parámetros de forma separada para cada grupo del segundo nivel y recoger la relación entre unidades de diferentes niveles. 3. Señala algunas ecuaciones clave de los modelos multinivel y las distintas estructuras de matrices de varianzas-covarianzas que se pueden adoptar.

1. MODELOS MULTINIVEL (MIXED)

2. La organización de los datos en el mundo real no responde a un solo nivel de análisis …
En la realidad tenemos variables que describen individuos, pero individuos que se
agrupan en unidades mayores (clases, colegios, estatus socioeconómico, grupos de
terapia…)
Esta estructura jerárquica afecta a los datos del primer nivel en el sentido de que
aquellos sujetos dentro de un grupo deben ser más parecidos entre sí…
Pero ¿cuál es el fundamento de un mixed?

3. Si los sujetos dentro de un grupo se parecen entre sí, asumimos que los datos dentro de
un grupo no son independientes entre sí, esto viola un supuesto muy importante dentro
del MLG. Los datos tienen una cierta correlación … sus residuales tienen una cierta
correlación y por tanto, no podemos estimar los parámetros del modelo a través de OLS
(Mínimos Cuadrados Ordinarios)

4. ¿Cómo manejamos esta dependencia de los datos?...
La correlación intraclase (ICC) es una medida de la dependencia de los datos..
La puntuación que obtiene un sujeto tiene una parte explicada por el grupo al que
pertenece… algo así como la cantidad de varianza que de las puntuaciones explica la
variable grupo…..sea mucha o poca .. ¿cómo afecta?
Si la variable grupo tiene un peso importante entendemos que los sujetos dentro del
mismo tendrán puntuaciones similares (baja variabilidad intragrupo)... y entre grupos
habrá grandes diferencias y por tanto una alta variabilidad…. Esto significa una ICC
alta..
La ICC nos dice cuán importante es el efecto de una variable contextual en la
puntuación final

5. Empecemos por una regresión simple…
Tenemos un modelo que nos genera predicciones sobre el rendimiento académico a
partir del CI…. En este caso hemos centrado La variable predictora para dar sentido al
intercepto…
Yi  508  2,15 X i  
Yi

6. Añadimos al modelo anterior una variable de agrupación de segundo nivel, tipo de
centro y llevamos a cabo un modelo de regresión simple para cada centro
Yprivado  547  2,5 X privado  
Ypúblico  492  2, 2 X público  

7. Sin embargo, no es necesario estimar modelos independientes en función de los J
niveles de la variable de segundo orden….es más práctico tener una sola ecuación
que tenga en cuenta los J niveles…
Yij  0 j  1 j X ij   ij
El modelo permite tener a cada centro su propia intersección y pendiente… esta
variabilidad del segundo nivel (Tipo de centro) genera un modelo multinivel, permite
recoger la relación de las unidades del primer nivel en cada grupo del segundo nivel. Por
tanto, β0j y βij ahora no son constantes sino variables cuyo valor depende del centro:
 0 j  b0  0 j  0 j   0  0 j
1 j  b1  1 j = 1 j   1  1 j

8. Parte aleatoria que refleja la
variabilidad de cada centro
respecto a esa media
poblacional, y con respecto a
la pendiente poblacional…
Parte fija o sistemática que representa los
valores poblacionales de media y
pendiente….
Un modelo con términos aleatorios en intercepto y pendiente genera tres posibles
situaciones de estudio….. la representación de estas tres ecuaciones son las
siguientes…

9. Intercepto Yij  (b0  0 j )  b1 X ij   ij
Aleatorio
Yij  b0 j  b1 X ij   ij
Pendiente
Yij  b0  (b1  1 j ) X ij   ij
Aleatoria Yij  b0  b1 j X ij   ij
Intercepto Yij  (b0  0 j )  (b1  1 j ) X ij   ij
Pendientes
Aleatorias Yij  b0 j  b1 j X ij   ij

10. Mismo intercepto Misma pendiente distinta pendiente
distintas pendientes distinto intercepto distinto intercepto

11. Las distintas ecuaciones que caracterizan a un modelo multinivel son…
Modelo de Regresión Simple
Yi   0  1 X 1  ei
Modelo Multinivel
Yi   0 j  1 j X 1 j  eij
 0 j   0  0 j término de intercepto aleatorio
1 j   1  1 j término de pendiente aleatoria
 0 j   00   01Z j  0 j variabilidad del intercepto 2ºnivel
1 j   10   11Z j  1 j variabilidad pendientes 2ºnivel
Modelo Completo parte fija y aleatoria
Yij   00   01Z j   10   11 xij Z j  ( 0 j  1 j  xij  eij )

12. Estructura de la matriz de varianzas-covarianzas ….
1. Los efectos aleatorios generan distintos patrones de matrices de
varianzas-covarianzas.
2. Las matrices de varianzas-covarianzas permiten estimar los parámetros de
nuestro modelo.
3. La estructura adoptada dependerá de si tenemos medidas repetidas o no,
o si asumimos covarianzas .
4. Es recomendable llevar a cabo varios análisis cambiado las estructuras de
covarianza y quedarnos con el modelo con mejor bondad de ajuste.
5. Las estructuras de covarianzas están relacionadas con lo liberal o
conservador del modelo, y por tanto, el Error Tipo 1 y Tipo 2
Las estructuras de v-c adoptadas son las siguientes…

13. Componentes de Varianza ( ajusta
cualquier modelo con interceptos Diagonal (Medidas Repetidas)
aleatorios
 2 0 0 0 
1 0 0 0  
   0 2 0 0 
 0 1 0 0  0 0 2 0 
0 0 1 0 
 0 
2
 0 0  
 
0 0 0 1
AR(1) (curvas de crecimiento, No estructurado (asumimos interceptos
datos medidos en el tiempo) y pendientes aleatorios, es por defecto
el modelo del SPSS)
 1  2 2 
    12  21  31  41 
 1  2   
  21  2  32  42 
2
 2  1 
 2    31  32  32  43 
 2  1   
   2 
 41  42  43  4 

14. ¿Cómo evaluamos la pertinencia o no de analizar los datos a través de un modelo
multinivel?
El primer paso es evaluar un modelo incondicional o nulo. Este modelo nos permite
observar la variabilidad dentro de los grupos y la variabilidad entre los grupos. Este
modelo se define (Raudenbush and Bryk, 2009) como ANOVA de efectos aleatorios. En
nuestro ejemplo de colegios…. y rendimiento…
Este modelo en el primer nivel nos indica que Este modelo en el segundo nivel nos indica
un sujeto obtiene como pronóstico en que el rendimiento por colegio es la
rendimiento la media de su colegio más una combinación del rendimiento para la
variabilidad aleatoria o error alrededor de población de colegios y la variación de cada
esa media colegio entorno a esa media
Yij  0 j  eij 0 j   00  0 j

15. Estimar este modelo nulo nos permite valorar el ICC.
Sí el ICC nos dice el grado de variabilidad en rendimiento académico entre colegios con
respecto al grado de variabilidad dentro de cada colegio podemos hacernos una idea de
cuánta de la variabilidad del rendimiento es explicado por una variable de segundo nivel
como es el colegio. Si encontramos que el ICC es de un 45% este porcentaje es lo que la
variable colegio explica del rendimiento…
¿Cómo evaluamos la bondad de un modelo Multinivel?
Un Modelo Multinivel se da por bueno cuando hemos conseguido aquel que de manera
más parsimoniosa explica mejor la variabilidad de los datos. Si bien tenemos distintos
indicadores de bondad AIC, BIC, etc… el más fiable es el contraste sobre la -2LL
(Logaritmo de la Verosimilitud/Verosimilitud restringida)… donde la diferencia entre
modelos sigue una distribución ji-cuadrado con grados de libertad como la diferencia de
número de parámetros evaluados en cada modelo….

16. Imaginemos que hemos evaluado dos modelos y hemos obtenido para ambos los
siguientes valores de -2LL.
 cambio  1852,5  1837, 49  15, 05
2
df cambio  5  4  1
  15, 05; p  0, 05
2
1
La bondad del segundo modelo se estima comparando con el primero modelo. Se
entiende que los modelos se van complejizando cada vez más… lo que implica
aumentar el número de parámetros a estimar….

17. Se estudio una población de 379 pacientes con trastorno depresivo que habían recibido tratamiento
en 11 hospitales. Se midieron variables como la puntuación en depresión con la escala de Hamilton,
sexo, tipo de centro (público vs. privado), edad media de los pacientes de cada centro, la VD es la
medida de recuperación 6 semanas después del tratamiento…. (Pardo, Ruíz y San Martín; 2007)

18. Empezamos estimando el modelo incondicional o nulo. Es en realidad un ANOVA de
efectos Aleatorios (AEA) para nuestro ejemplo tratamos la clínica como factor
aleatorio. La ecuación que define este modelo sería…
Yij  b0 j  eij  b0 j  b0  0 j
La puntuación media poblacional de los
11 centros en Recuperación es 9,15
Cuánto varía VD entre los centros (9,09)
y cuánto varía dentro de los centros
(18,0)

19. El modelo nulo nos cuenta dos cosas muy importantes…
1. Cuánta variabilidad hay entre los centros.
2. Cuánta variabilidad hay dentro de los centros.
9, 09
ICC      
9, 09  18, 00
Atendiendo al coeficiente de correlación intraclase, encontramos que el 34% de la
variabilidad en la variable Recuperación se explica por las diferencias entre las medias
de los distintos clínicas o centros.
Un valor de uno indicaría que toda la variabilidad es debida al factor centro (todos los
pacientes dentro de un centro puntúan igual en recuperación y entre centros la media
es distinta) y un valor de cero es que todos los centros tienen el mismo promedio de
recuperación y la variabilidad está dentro de los centros.

20. Busquemos una variable de segundo nivel que nos explique esta diferencia en
recuperación entre centros… aquí incluimos una variable predictora de segundo nivel….
Elegimos la variable edad que nos da la edad promedio en cada centro por tanto es una
variable covariable a nivel 2…. Podemos hipotetizar que la diferencia de edad puede
estar explicando el alivio de los síntomas depresivos…
Observamos que el modelo de nivel 1 no cambia….
Yij  b0 j  eij
Es a nivel 2 donde incorporamos una variable predictora….
b0 j  b00  b01Z j  0 j
El modelo combinado final sería….. Yij  b00  b01Z j  (0 j  eij )

21. Por cada año que aumenta la edad la
recuperación media (9,5) disminuye en
0,39
La varianza de los residuos no ha cambiado
mucho con respecto al modelo anterior por
tanto la inclusión de cedad no ha afectado a la
variabilidad del nivel 1. Sin embargo hemos
reducido la variabilidad del nivel 2 a 2,69
(antes 9,09)

22. La inclusión de la variable cedad a permitido reducir la ICC a 13%, es decir, aun queda
un 13% de variabilidad entre centros en recuperación no explicado por la edad media
de los centros… el modelo ha mejorado en su explicación la diferencia entre modelos
de -2LL AIC nos muestra una mejora significativa….
2, 69
ICC     1
2, 69  17,99
Incluyamos una variable de nivel 1 para poder apresar más la variabilidad de
recuperación…. En este caso incluimos la variable nivel basales de recuperación. En este
caso el modelo cambia incorporando una variable de primer nivel…
Yij  b00  b01Z j  b10 xij  (0 j  eij )

23. A nivel poblacional la recuperación media es 9,05, la inclusión
de la pendiente cbasal nos dice que por cada unidad que
aumenta cbasal la recuperación lo hace en 0,21.
Se reduce ligeramente la variabilidad entre centros (2,69 a
2,29). Sin embargo, se reduce de 18 a 16

24. Hasta ahora sólo hemos considerado que el intercepto es aleatorio, es la variable centro
la única que consideramos aleatoria.. Los demás efectos los hemos considerado fijos
bien sea la edad media de cada centro, como el nivel basal de depresión de los
pacientes…. Estos modelos se llaman constantes
Estimemos un modelo que contempla también las pendientes como aleatorias….
En el caso anterior consideramos las puntuaciones basales eran homogéneas en todos
los centros…. Estimemos ahora una ecuación de regresión para cada centro para
estimar cuánto de la variabilidad intracentro es explicado por las puntuaciones
basales…
Lo que estamos viviendo no sólo es en cuánto se diferencian los centros en el grado de
recuperación sino que relación existe entre el grado de recuperación y las puntuaciones
basales… es decir estimamos intercepto y pendiente aleatoria…. Dado que asumimos
interceptos y pendientes aleatorias tenemos que cambiar la matriz de varianzas-
covarianzas a sin estructura en el SPSS…
Yij  b00  b10 xij  (0 j  1 j xij  eij )

25. A nivel poblacional la recuperación media es 9,14, la
inclusión de la pendiente media cbasal cuyo valor es 0,37 y
dice que por cada punto de incremento a nivel poblacional
en cbasal la recuperación poblacional aumenta 0,37
puntos.
Se reduce ligeramente la variabilidad intracentro (12,64)…
la varianza de las medias (intersecciones) es significativa
NE(1,1) varianza de las medias o intersecciones… (6,02)… las varianza de las pendientes es significativa (0,11)
NE(2,2) varianza de las pendientes.. NE(2,1) covarianza por tanto las pendientes son distintas en función del
entre ambas… centro… la covarianza pendientes interceptos no es
significativa (0,21) parece que no hay relación entre estas…

26. Resumiendo:
1. La varianza de los residuos nos dice que parece que incluyendo las puntuaciones basales la
variabilidad intracentro se reduce en un 30%
(18, 00  125, 64)
 0, 29  30%
18.00
2. La varianza de las intersecciones (6,03) nos dice que la recuperación media de los centros no
es la misma
3. La varianza de las pendientes (0,11) nos dice que las pendientes no son iguales en todos los
centros. La relación entre puntuaciones basales y grado de recuperación no es la misma en
todos los centros.
4. La relación intracentro entre pendientes e interceptos no es significativa (0,21) por tanto la
relación intracentro entre medias y pendientes no parece ir aumentando o disminuyendo
conforme lo hace el tamaño de las medias.

27. Hemos visto que… los interceptos y pendientes varían de centro a centro…. la
recuperación no es la misma en los centros, que la relación entre las puntuaciones
basales y la recuperación no es la misma en todos los centros… básicamente
observamos los interceptos por centros, las pendientes por centro y la relación
intercepto pendientes por centro…
Justamente un modelo multinivel lo que busca es relacionar precisamente los niveles
del diseño.. Encontramos que la variabilidad intercentros en recuperación en un 70%
era explicada por la edad media de los centros (valores aleatorios de intercepto)....
Ahora nos faltaría ver qué hace que las pendientes sean distintas entre centros… qué
variable justifica la variabilidad de las pendientes observadas en este último análisis…
.. para ello incluimos una variable que se llama sector (centro público o privado).. En
este caso incluimos una variable de 2º nivel como aleatoria….

28. El modelo que interpreta las intersecciones y las pendientes como resultados es…
a nivel 1….. Yij  b00  b01 xij ij
0 j  b00  b01 z j  b02 w j  0 j
…a nivel 2 sería..
1 j  b10  b11 z j  b12 w j  1 j
El modelo multinivel , o mixto de efectos fijos y aleatorios completamente
especificado sería……
Yij  b00  b01 z j  b02 w j  b10 xij  b11 xij z j  b12 xij w j
( 0 j  1 j xij  eij )

29. Si incluimos las etiquetas de las variables en la ecuación se ve más claro…
(espero!!)..
Efectos principales cedad (N1), sector(N2) y cbasal(N1)
Yij  b00  b01 (cedad ) j  b02 (sec tor ) j  b10 (cbasal )ij
b11 (cbasal )ij (cedad ) j  b12 (cbasal )ij (sec tor ) j
( 0 j  1 j (cbasal )ij  eij )
Interacción 1: cbasal y cedad. Interacción 2: cbasal y
¿Se ve afectada la relación sector. ¿Se ve afectada la
entre recuperación y nivel relación entre recuperación
basal cuando cambia la edad y nivel basal cuando cambia
media del centro? el tipo de centro?

30. La recuperación media poblacional sigue siendo la misma 9,91. Ahora controlando el tipo de centro(sector)
encontramos que la variable edad media del centro afecta al nivel de recuperación en sentido negativo…por cada
año que aumenta disminuye la recuperación en 0,25. Por otro lado controlando el efecto de la edad (cedad) no
parece que el tipo de centro afecte a la recuperación (-1,20)… las puntuaciones basales muestran que por cada
incremento de la puntuación basal la recuperación se incrementa en 0,58. La interacción cedad*cbasal nos dice
que los cambios en edad no alteran las relaciones entre cbasal y recuperación, las pendientes son muy parecidas
en los gráficos de la siguiente transparencia. La interacción sector*cbasal muestra que el tipo de centro se
relaciona negativamente con las pendientes. En los centros públicos (valor cero en la dummy) es mayor que en los
centros privados

31. cedad
Nivel de Recuperación
En los efectos aleatorios… la varianza de los residuos es 12,73 muy parecido a la
anterior de modelo de coeficientes aleatorios…. La varianza de las medias o
intersecciones es 3,45 (en el modelo anterior fue 6,03) .. La incorporación de cedad y
sector y una vez contrado el efecto de la puntuación basal, estas variables explican el
42,7% de la varianza entre las medias de los centros. Igual que en el modelo anterior
parece que las medias o intersecciones no están relacionadas con las pendientes
(NE21).. Finalmente ahora las pendientes han dejado de ser distintas de cero
significativamente… es decir una vez controlado el efecto de cedad y sector,
desaparecen las diferencias entres las pendientes de los distintos centros

32. Como conclusión y atendiendo al índice -2LL AIC no parece que este modelo mejore
significativamente al modelo que no incluye pendientes aleatorias. Por tanto nos
quedaríamos con dicho modelo dado que es más parsimonioso..
Hasta ahora hemos visto un acercamiento al análisis mixto o multinivel en el que
asumiendo la jerarquía de los datos comenzamos estimando un modelo nulo para
acabar por definir el modelo completamente aleatorizado en interceptos y pendientes
con términos de interacción entre niveles (Raudenbush y Bryk; 2002)
Sin embargo tal y como plantea Field (2010) quizás sea más ilustrativo comenzar
pensando en que un análisis multinivel no es más que una extensión del MLG , en
realidad lo único que cambia es que la estimación de los parámetros de la recta no se
lleva a cabo por OLS sino por ML o MLR…Veamos esta otra manera de acercarnos a
los modelos multinivel…..

33. Veamos un ejemplo…. (Field 2010). Se pretende modelar el efecto que la cirugía estética
tiene sobre la calidad de vida del paciente medida después de la intervención… (Field,
2010)

34. Mixed Tipo ANOVA
Mixed Tipo ANCOVA
Hasta ahora hemos ignorado la estructura jerárquica de nuestros datos…. Y por tanto
estamos violando un supuesto y es que las observaciones no son independientes entre
sí…. Por tanto asumamos esta violación y analicemos los datos jerárquicamente….
Empezamos asumiendo interceptos aleatorios, es decir que hay una variable que agrupa
los datos. Esta variable es clinic una variable que está en el 2ºnivel
QoLij  b0 j  b1Surgeryij  b2QoLbeforeij  eij

35. Evaluación de la bondad del modelo a través de -2LL
AIC…. Comparando con los anteriores ganamos en
explicación… contraste ji-cuadrado con gl = 1
el nivel de calidad de
vida no es el mismo
atendiendo a la clínica…
Cuánto varía la calidad de vida
entre las clínicas.. Variabilidad
Cuánto varía la calidad de vida “intergrupos”
dentro de cada clínica.. Variabilidad
“intragrupos” o error
9, 23
ICC   
9, 23  42, 49

36. Ahora generamos un modelo donde añadimos una pendiente aleatoria…que es la
covariable surgery manteniendo la variable clinic como aleatoria de 2ºnivel.. El modelo
queda especificado en la siguiente ecuación….
QoLij  b0 j  b1 j Surgeryij  b2QoLbeforeij  eij

37. Evaluación de la bondad del modelo a través de -2LL
AIC…. Comparando con los anteriores ganamos en
explicación… contraste ji-cuadrado con gl = 1
33,18
ICCint erceptos   
33,18  35, 00
29, 63
ICC pendientes   
29, 63  35, 00
La variabilidad en los interceptos
La variabilidad entre las pendientes

38. Sin embargo en ese modelo no asumimos una estructura de covarianza que asuma
que los interceptos aleatorios y las pendientes aleatorias correlacionen…. En este
caso lo que hacemos es cambiar la estructura de covarianzas en los factores
aleatorios a “sin estructura”….
Observamos como a mejorado la bondad del
modelo con la disminución del índice -2LL AIC….
Comparando con el anterior de 1816. Esta
diferencia es significativas con lo que estimamos
que este nuevo modelo mejora el anterior…

39. La variabilidad en los interceptos
Covarianza interceptos-pendientes
La variabilidad entre las pendientes
 37, 60 36, 68 
Matriz de V-C  
 36, 68 38, 40 

40. El valor negativo de la covarianza interceptos pendientes (-36,68) indica que a través
de las clínicas a medida que el intercepto (media) entre surgery y QoL aumenta la
pendiente decrece, lo que implica que observando el gráfico a medida que aumenta
el valor del intercepto disminuye la pendiente de la recta…

41. Finalmente incorporando el término interacción…. Para ello incorporamos la variable
reason for surgery….
QoLij  b0 j  b1Surgeryij  b2QoLbeforeij  b3 Re asonij
b4 Re ason * Sureryij  eij
Observemos que el modelo sigue siendo de interceptos aleatorios y pendientes
aleatorias a lo que hemos añadido el término interacción… dado que Surgery es una
variable de 2ºnivel llevamos a cabo una interacción permitimos la relación de las
variables de primer y segundo nivel…. Algo que es justamente la ventaja de los
modelos multinivel….poder modelar la influencia de variables de agrupación jerárquica
sobre variable del sujeto…

42. Interpreta el resultado……

43. Gracias!!!!