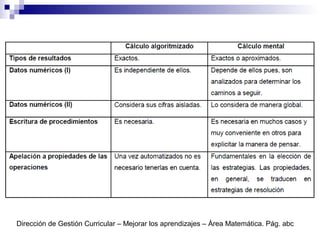
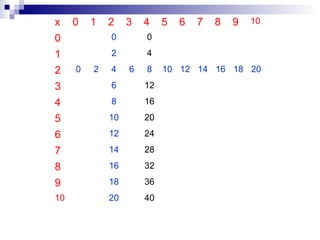
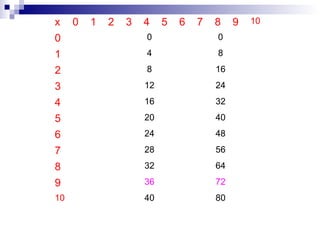
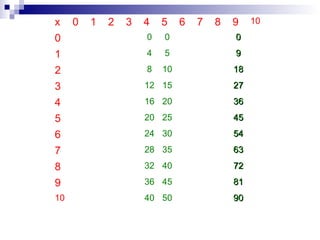
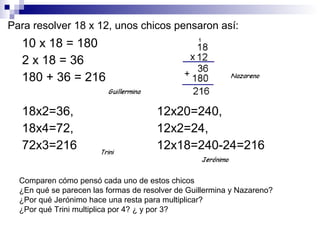
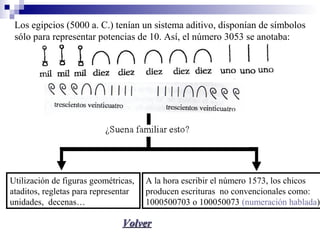
El documento discute el sistema de numeración decimal. Explica que es un sistema compuesto de 10 signos que pueden combinarse para representar cualquier número. Es un sistema decimal basado en 10, posicional donde el valor de una cifra depende de su posición, y mixto que usa la adición y la multiplicación. Se escriben los números en orden decreciente de izquierda a derecha.

1. ADROGUÉ
Colegio Irlandés
NÚMEROS Y OPERACIONES
MATEMÁTICAMATEMÁTICA

2. Algunas cuestiones a tener en cuenta respecto de nuestro sistema:Algunas cuestiones a tener en cuenta respecto de nuestro sistema:
La utilización permanente de nuestro sistema nos hace perder de vista su
complejidad.
Es una creación cultural con características propias que difieren de las
de otros sistemas pertenecientes a otras culturas. ¿Cuáles?¿Cuáles?
Las investigaciones didácticas en nuestro país y en otros, demuestran que
los famosos “me llevo uno” y “le pido una al compañero”, ritual inherente
a las cuentas escolares, no tienen ningún vínculo con las unidades, decenas
y centenas, estudiadas previamente
1250
+1250
_____________________________
13750
1250
+ 1250
_________________________
24100
Como cualquier objeto de construcción cultural es una convención y como
tal es arbitrario, por lo tanto, depende de la enseñanza para que pueda ser
aprendido por las nuevas generaciones. Veamos un ejemplosVeamos un ejemplos

3. ¿QUÉ DICE EL DISEÑO A TODO ESTO?¿QUÉ DICE EL DISEÑO A TODO ESTO?
Una cuestión a identificar es que el análisis del valor posicional del sistema de
numeración en términos de unidades, decenas y centenas no forma parte de los
contenidos de primer ciclo ya que exige un dominio de la multiplicación y la división
por potencias de 10. Por ejemplo, para los alumnos/as de primer ciclo sí es posible
poner en juego - en problemas y cálculos - que 748= 700 + 40 + 8 o bien que para
pagar $748 se puede usar tanto 7 billetes de cien, 4 de diez y 8 monedas de 1,
como 74 billetes de 10 y 8 monedas de 1. Pero comprender que en el número 748
hay 74 decenas y 8 unidades (pues 74 x 10 = 740), o que 748 puede ser pensado
como 7 x 100+ 4 x 10 + 8 x 1 (para interpretar 7 centenas, 4 decenas y 8 unidades)
son sin duda operaciones posibles para el 2º ciclo; así como identificar que
748 = 7 x 102
+ 4 x 101
+ 8 x 100
será objeto de trabajo en los primeros años de la
Escuela Secundaria. No se trata de que los alumnos/as memoricen nombres de
posiciones (unidad, decena, centena) carentes de relaciones. Comprender la
estructura profunda del sistema de numeración demandará varios años de trabajo
a los alumnos/as, y en cada año se abordarán algunos aspectos en función de la
complejidad y los conocimientos que requieren.
Diseño curricular para la Educación Primaria

4. SIN USAR ALGORITMOS, ENCUENTRE EL
RESULTADO DEL SIGUIENTE CÁLCULO DE
LA MANERA MAS CONVENIENTE.
EXPLIQUE, EN CADA CASO, CÓMO LO
RESOLVIÓ.
483 + 357 =

5. 483 + 357 = (483 + 300) + 57
= 783 + 57
= 783 + 7 + 50
= 790 + 10 + 40
= 840

6. 483 + 357 = 480 + 350 + 3 + 7
= 480 + 350 + 10
= 480 + 360
= 480 + 20 + 340
= 500 + 340
= 840

7. SIN USAR ALGORITMOS, ENCUENTRE EL
RESULTADO DEL SIGUIENTE CÁLCULO DE
LA MANERA MAS CONVENIENTE.
EXPLIQUE, EN CADA CASO, CÓMO LO
RESOLVIÓ.
720 – 290 =

8. 720 – 290 = 600 + 120 – 200 – 90
= 600 – 200 + 120 – 90
= 400 + 30
= 430

9. 720 – 290 = 420 + 300 – 290
= 420 + 10
= 430

10. SIN USAR ALGORITMOS, ENCUENTRE EL
RESULTADO DEL SIGUIENTE CÁLCULO DE
LA MANERA MAS CONVENIENTE.
EXPLIQUE, EN CADA CASO, CÓMO LO
RESOLVIÓ.
180 x 25 =

11. 180 x 25 = 100 x 25 + 80 x 25
= 100 x 25 + 2 x 2 x 2 x 25 x 10
Como 80 = 8 x 10 y
multiplicar por 8 es igual que multiplicar por 2 x 2 x 2
Entonces
El doble de 25 es 50, el doble de 50 es 100
y el doble de 100 es 200
= 2500 + 200 x 10
= 2500 + 2000
= 4500

12. 180 x 25 =
=180 x 20 + 180 x 5
= 180 x 2 x 10 + 180 x 5
= 360 x 10 + 180 x 10 : 2
= 3600 + 1800 : 2
= 3600 + 900
= 3600 + 1000 - 100
= 4500

13. 180 x 25 =
25 x 2 = 50
25 x 20 = 500
25 x 200= 5.000
Como 180 = 200 - 20
Entonces 180 x 25 = 5.000 - 500

14. Halle el resultado de 634 – 369
de tres formas diferentes.
Explique cada una de ellas

15. Estrategias a desarrollar
Sumar Restar
Unos 27+1= 35-1=
Dieces 75+20 = 95 238-10=228
Cienes 438+300 = 738 6.576-400=6.176
Miles 2.567+2.000=4.567 …
…

16. Estrategias a desarrollar
Suma de iguales
4+4=
5+5=
7+7=
…
40+40=
50+50=
70+70=
…
400+400=
500+500=
700+700=
…
4.000+4.000=
5.000+5.000=
7.000+7.000=
…

17. Si tachamos las parejas de números que suman 10,
¿qué número queda sin tachar?
Estrategias a desarrollarEstrategias a desarrollar
Sumas que dan diezSumas que dan diez

18. Estrategias a desarrollarEstrategias a desarrollar
Sumas que dan diezSumas que dan diez
Si tachamos parejas de números que suman 10,
¿qué números quedan sin tachar?

19. Si tachamos las parejas de números que suman 100,
¿qué número queda sin tachar?
Estrategias a desarrollar
Sumas que dan cienSumas que dan cien

20. Estrategias a desarrollar
Sumar
Número redondo (nudo) más
otro número
Restar
Para que la diferencia sea un
número redondo (nudo)
40+7= 47-7=
200+38= 238-38=
2.000+679= 2.679-679=
… …

21. Sin hacer la cuenta, decidí cerca de qué
número van a dar los siguientes cálculos:
420 + 196 = 500 600 700
309 + 403 = 300 500 700
720 – 219 = 600 500 400
……………
Dirección de Gestión Curricular – Mejorar los aprendizajes – Área Matemática. Pág. abc

22. ¿Qué es el cálculo mental? ¿Qué lo
diferencia de los algoritmos de
cálculo que siempre hemos enseñado?
¿Por qué en el diseño curricular se
propone trabajar con cálculo mental
antes de hacerlo con los algoritmos?
Dirección de Gestión Curricular – Mejorar los aprendizajes – Área Matemática.
Pág. abc

23. … definiciones de cálculo mental y algorítmico*:
Cálculo Algorítmico: serie de reglas aplicables en un
orden determinado, independientemente de los datos, que
garantizan alcanzar un resultado en un número finito de
pasos.
Cálculo mental: conjunto de procedimientos que,
analizando los datos por tratar, se articulan sin recurrir a
un algoritmo preestablecido para obtener resultados
exactos o aproximados.
*Dirección de Gestión Curricular – Mejorar los aprendizajes – Área Matemática.
Pág. abc

24. Dirección de Gestión Curricular – Mejorar los aprendizajes – Área Matemática. Pág. abc

25. Sin hacer la cuenta tradicional,
encuentren el resultado de
2.357 x 18

26. Usando que 18 × 24 = 432, encuentren el
resultado de cada uno de los siguientes
cálculos sin hacer la cuenta tradicional:
18 x 12 = 9 x 24 = 9 x 12=
18 x 48 = 36 x 24 = 36 x 12=
180 x 24= 180 x 240 = 180 x 12 =

27. Analicen en grupos cómo se presentan
las tablas de multiplicar en las aulas

28. Las situaciones de trabajo con la tabla
pitagórica favorecen la construcción de un
repertorio de cálculos multiplicativos a partir del
análisis de las regularidades y propiedades de
la multiplicación y la división. Los niños pueden
completar la tabla focalizando en algunas
relaciones, por ejemplo:
Dirección de Gestión Curricular – Mejorar los aprendizajes – Área Matemática. Pág. abc

29. x 0 1 2 3 4 5 6 7 8 9 10
0 0 0
1 2 4
2 0 2 4 6 8 10 12 14 16 18 20
3 6 12
4 8 16
5 10 20
6 12 24
7 14 28
8 16 32
9 18 36
10 20 40

30. x 0 1 2 3 4 5 6 7 8 9 10
0 0 0
1 4 8
2 8 16
3 12 24
4 16 32
5 20 40
6 24 48
7 28 56
8 32 64
9 36 72
10 40 80

31. x 0 1 2 3 4 5 6 7 8 9 10
0 0 0 00
1 4 5 99
2 8 10 1818
3 12 15 2727
4 16 20 3636
5 20 25 4545
6 24 30 5454
7 28 35 6363
8 32 40 7272
9 36 45 8181
10 40 50 9090

32. … Si alguien no recuerda 9 x 8, es posible reconstruirlo.
Por ejemplo,
 vimos que 9 x 8 es el doble de 9 x 4 entoncesvimos que 9 x 8 es el doble de 9 x 4 entonces
9 x 8 = 9 x 4 x 2 = 36 x 2 = 729 x 8 = 9 x 4 x 2 = 36 x 2 = 72
 9 x 8 = 9 x 5 + 9 x 3 = 45 + 27 = 729 x 8 = 9 x 5 + 9 x 3 = 45 + 27 = 72
 9 x 8 = 5 x 8 + 4 x 8 = 40 + 32 = 729 x 8 = 5 x 8 + 4 x 8 = 40 + 32 = 72
 10 x 8 – 8 = 80 – 8 = 7210 x 8 – 8 = 80 – 8 = 72
 9 x 10 – 9 x 2 = 90 – 18 = 72;9 x 10 – 9 x 2 = 90 – 18 = 72;
etcétera.
Estas “pistas” quedarán registradas en las carpetas paraEstas “pistas” quedarán registradas en las carpetas para
que los alumnos puedan volver sobre ellas las veces queque los alumnos puedan volver sobre ellas las veces que
lo consideren necesario. Todo este bagaje delo consideren necesario. Todo este bagaje de
conocimientos constituirá una trama que contribuirá alconocimientos constituirá una trama que contribuirá al
trabajo de memorización de las tablas.trabajo de memorización de las tablas.

33.  Proponer a los alumnos/as jugar a la “tapadita”:Proponer a los alumnos/as jugar a la “tapadita”:
el docente muestra la tabla pitagórica del afiche completa,el docente muestra la tabla pitagórica del afiche completa,
pero con algunos casilleros tapados, y los alumnospero con algunos casilleros tapados, y los alumnos
deberán anotar en sus cuadernos los resultados de lasdeberán anotar en sus cuadernos los resultados de las
multiplicaciones que se encuentran ocultos (sin consultarmultiplicaciones que se encuentran ocultos (sin consultar
sus tablas pitagóricas personales).sus tablas pitagóricas personales).
 Presentar tablas completas con algunos erroresPresentar tablas completas con algunos errores
para que los alumnos/as las corrijan.para que los alumnos/as las corrijan.

34. Menos de
1.000
Entre
1000 y
10.000
Más de
10.000
201 x 8
399 x 20
789 x 105
Marcá con una cruz entre qué números, aproximadamente,
va a estar el resultado de cada cálculo sin resolverlos y
explicá cómo te diste cuenta.

35. ¿Para qué sirve poder estimar¿Para qué sirve poder estimar
el resultado de un cálculo?el resultado de un cálculo?

36. Para resolver 18 x 12, unos chicos pensaron así:
10 x 18 = 180
2 x 18 = 36
180 + 36 = 216
18x2=36,
18x4=72,
72x3=216
12x20=240,
12x2=24,
12x18=240-24=216
Comparen cómo pensó cada uno de estos chicos
¿En qué se parecen las formas de resolver de Guillermina y Nazareno?
¿Por qué Jerónimo hace una resta para multiplicar?
¿Por qué Trini multiplica por 4? ¿ y por 3?

40. VolverVolver
El sistema está compuesto de 10 signos que combinados entre si,
pupueden representar cualquier número.
Es un sistema decimal porque está organizado en base 10, es decir que
cada unidad de un orden equivale a 10 unidades del orden anterior.
Es además un sistema posicional porque la misma cifra posee diferente
valor según la posición que ocupe: por ejemplo, la cifra 7 vale diferente
en 7, 70, 700, etc. Esta organización procura una enorme economía
tanto para anotar o leer los números como también para operar con ellos.
Es un sistema mixto: multiplicativo y aditivo.
Se escribe en orden decreciente de izquierda a derecha: las cifras que
representan cantidades mayores a la izquierda y las menores a la derecha.
Incluye el cero.
Entre dos números de la misma cantidad de cifras, es mayor el que tiene
a la izquierda el número mayor.
Entre dos números de diferente cantidad de cifras, es mayor el que tiene
más cifras.

41. Los egipcios (5000 a. C.) tenían un sistema aditivo, disponían de símbolos
sólo para representar potencias de 10. Así, el número 3053 se anotaba:
Utilización de figuras geométricas,
ataditos, regletas para representar
unidades, decenas…
A la hora escribir el número 1573, los chicos
producen escrituras no convencionales como:
1000500703 o 100050073 (numeración hablada)
VolverVolver

42. NUMERACIÓN HABLADANUMERACIÓN HABLADA
Es no posicional
La yuxtaposición de palabras supone siempre una operación aritmética
Mil cuatro significa 1000 + 4
Ochocientos significa 8 x 100
Cinco mil cuatrocientos significa 5 x 1000 + 4 x 100
Cinco mil es 5 x 1000
Mil cinco es 1000 + 5
Didáctica de las matemáticas-Aportes y reflexiones-Parra C., Sainz I.
A estas complejidades hay que sumarle que la conjunción “y”, que
representa lingüísticamente la adición, solo aparece cuando se trata de
reunir decenas y unidades y no en la reunión de centenas y unidades.
VolverVolver