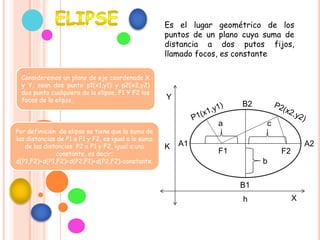
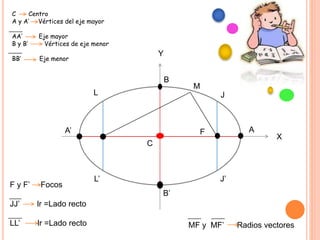
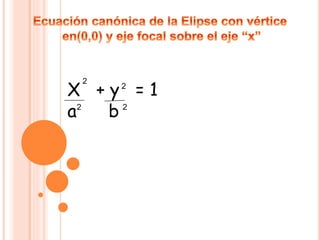
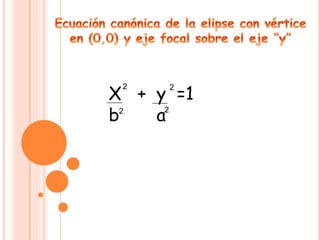
El documento se centra en la definición y características de la elipse, incluyendo sus focos, ejes, vértices y propiedades geométricas. Se explican conceptos clave como la excentricidad, distancias focales y la relación entre los ejes mayor y menor. Además, se presentan ejemplos para calcular la ecuación canónica de una elipse y las coordenadas de sus focos.

1. Republica Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
U.E. Colegio “Del Santísimo”
Barquisimeto Edo Lara
Integrantes:
Jenny Carieles#08
Kielis Ortegas#31
Anais Oviedo#32
Profesor:
Miguel GerdezBarquisimeto,2018

2. Es el lugar geométrico de los
puntos de un plano cuya suma de
distancia a dos putos fijos,
llamado focos, es constante
A1
B1
A2
B2
a
b
c
F1 F2
X
Y
Consideremos un plano de eje coordenada X
y Y, sean dos punto p1(x1,y1) y p2(x2,y2)
dos punto cualquiera de la elipse, F1 Y F2 los
focos de la elipse.
K
h
Por definición de elipse se tiene que la suma de
las distancias de P1 a F1 y F2, es igual a la suma
de las distancias P2 a F1 y F2, igual a una
constante, es decir;
d(P1,F2)+d(P1,F2)=d(P2,F1)+d(P2,F2)-constante.

3. Si tenemos un punto P(x,y) de la elipse, escribiremos:
d(P1,F1)+d(P2,F2)=2a donde la constante,F1 F2 es el eje focal. La
distancia entre los dos focos, llamada distancia focal es igual a 2c.
d(F1,F2)=2C
A1 A2,B1 y B2 son los vértices de la elipse.
A1 A2 es el eje mayor y siempre va a contener los dos focos. La
diferencia entre los dos vértices A1 y A2 en igual a 2ª.
d(A1,A2)=2ª
B1 B2 es el eje menor y nunca contiene a los focos. La diferencia
entre los dos vértices B1 y B2 es igual a 2b.
d(B1,B2)=2b
El centro de la elipse C(h,k), es el puno medio entre A1 y A2, B1 y
B2, F1 y F2. la excentricidad de una elipse, viene dada e=c/a,
donde siempre 0<e<j.
Los valores a,b y c, se relacionan con la formula: a1=b2+c2
Según la definiciones anteriores se tiene que:
d(A1,C) = d(A2.C) =a longitud del semieje mayor.
d(B1,C) = d(B2,C) =b longitud del semieje menor
d(F1,C) = d(F2,C) =C longitud del semieje focal.

4. 1- focos: son los puntos fijo F y F’.
2- Eje focal: es la recta que pasa por los focos.
3- Eje secundario: es la mediatriz del segmento FF’.
4- Centro: es el punto de intersección de los ejes.
5- Radios vectores: son los segmento que va desde un punto
de la elipse a los focos: PF y PF’.
6- Distancia focal: es el segmento de longitud 2c, c es el
valor de la semidistacia focal.
7- Vértices: son los puntos de intersección de la elipse con
los ejes: A, A’, B y B’.
8- Eje mayor: es el segmento de la longitud 2ª, a es el valor
del semieje mayor.
9- Eje menor: es el segmento de longitud 2b, b es el valor de
semieje menor.
10- Ejes de simetría: son las recta que contienen al eje
mayor o a el eje menor.
11- Centro de simetría: coincide con el centro de la elipse,
que es el punto de intersección de los ejes de simetría.

5. Y
X
A’ A
L
L’
B
B’
C
M
F
J
J’
C Centro
A y A’ Vértices del eje mayor
AA’ Eje mayor
B y B’ Vértices de eje menor
BB’ Eje menor
F y F’ Focos
JJ’ lr =Lado recto
LL’ lr =Lado recto MF y MF’ Radios vectores

6. X + y = 1
a b
2
2
2
2

7. X + y =1
b a
2 2
2 2

8. Vemos que el semieje menor esta situado sobre el
eje X y en consecuencia la ecuación será de la
forma
Además, los focos están sobre el eje “Y” y
están dados por
Luego: la ecuación pedida es
y los focos son
Ejemplo:
Hallar los focos y la ecuación canónica de una elipse con
vértices
Solución :

9. (x – h) _ (y – k)
a b2
2 2
2
Donde a > b > o y a =b + c
2 2 2

10. (x – h) + (y – k)
b a
2
2
2
2

11. Ax^2+By^2+Cx+Dy+E=0

12. Hallar las coordenadas del centro y de los focos de la elipse cuya ecuacion
general es
9x + 4y - 54x – 40y +145=0
2 2
Solución:
Expresamos la ecuación general en forma canónica organizando los trinomios y completando para
factorizar:
9(x - 6x) + 4(y - 10y)= -145
9(x - 6x + 9) + 4(y - 10y + 25) = -145 + 81 + 100
2 2
2 2
Dividimos entre 36:
9(x – 3) + 4 (y – 5) =36
(x – 3) + (y – 5) =1
4 9
2 2
22

13. Luego: las coordenadas del centro son (3,5)
Como
C = a - b c = 5,c = - raiz de 5
Luego: las coordenadas de los focos son:
F1: (3,5+ raiz de 5) y F2: (3,5 – raiz de 5)
+2 2 2 2