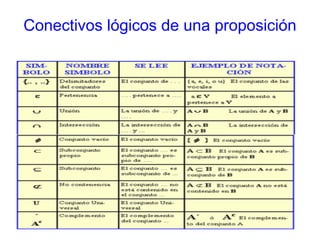
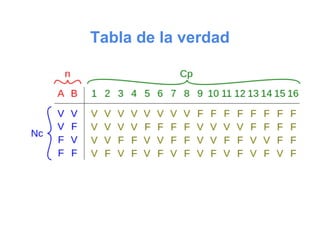
Este documento trata sobre proposiciones lógicas. Explica que una proposición es una expresión lingüística con contenido informativo, y no se identifica con la oración. Describe los conectivos lógicos que conectan proposiciones, como la conjunción y la disyunción. También cubre formas proposicionales, leyes del álgebra proposicional, razonamientos y métodos de demostración como reducción al absurdo y método directo.

1. PROPOSICIONES
LÓGICAS
LEONARDO VILLARREAL
CI. 19528951

2. UNA PROPOSICIóN
Una proposición es entendida
generalmente en el contexto de la
lógica como una expresión
lingüística cuya función es
informativa.
La proposición no se identifica con la oración sino
con su contenido descriptivo o su carga informativa,
pudiendo haber diferentes oraciones que sean la
misma proposición desde el punto de vista lógico.

3. Conectivos lógicos de una
proposición
En lógica, una conectiva lógica, o
simplemente conectiva, es un símbolo que
se utiliza para conectar dos fórmulas, de
modo que el valor de verdad de la fórmula
compuesta dependa del valor de verdad de
las fórmulas componentes.
Las conectivas lógicas son, junto con los
cuantificadores, las principales constantes
lógicas de muchos sistemas lógicos,
principalmente la lógica proposicional y la
lógica de predicados.

4. Conectivos lógicos de una proposición

5. Formas proposicionales
Son fórmulas veritativo funcionales, o sea, de
qué modo son susceptibles de adoptar uno u
otro valor de verdad según las proposiciones
simples que contengan sean verdaderas o falsas
y según el significado de las conectivas que las
unen.
Ejemplo
Si p es la proposición
P: Barcelona es un
estado Oriental.

6. Leyes del algebra proposicional
Las leyes de la algebra de proposiciones son
equivalencias lógicas que se pueden demostrar con el
desarrollo de las tablas de verdad del bicondicional
Leyes de Conjunción Leyes de disyunción
inclusiva
Leyes de Morgan

7. Razonamientos
Diremos que un razonamiento es válido o correcto si la conjunción de
premisas implican lógicamente la conclusión, en otro caso se dice que es
no válido.
Un razonamiento que no es válido es llamado falacia.
Ejemplo 2: El siguiente es otro
razonamiento lógico:
Si el animal vuela, entonces el animal
tiene alas.

8. Métodos de Demostración
Método reducción al
absurdo
Método Directo
En la demostración directa
debemos probar una implicación:
P Þ q. Esto es, llegar a la
conclusión q a partir de la premisa p
mediante una secuencia de
proposiciones en las que se utilizan
axiomas, definiciones, teoremas o
propiedades demostradas
previamente
Veamos que la proposición p
Þ q es tautológicamente
equivalente a la proposición (p
Ù ~ q) Þ (r Ù ~ r) siendo r una
proposición cualquiera, para
esto usaremos el útil método
de las tablas de verdad.

9. Tabla de la verdad

10. Inferencia
Una inferencia es una evaluación que realiza la
mente entre expresiones bien formadas de un
lenguaje (EBF) que, al ser relacionadas
intelectualmente como abstracción, permiten
trazar una línea lógica de condición o
implicación lógica entre las diferentes EBF. De
esta forma, partiendo de la verdad o falsedad
posible (como hipótesis) o conocida (como
argumento) de alguna o algunas de ellas, puede
deducirse la verdad o falsedad de alguna o
algunas de las otras EBF.

11. Circuitos lógicos
Los circuitos lógicos o redes de conmutación los podemos identificar
con una forma proposicional. Es decir, dada una forma proposicional,
podemos asociarle un circuito; o dado un circuito podemos asociarle la
forma proposicional correspondiente.