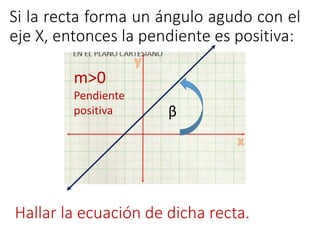
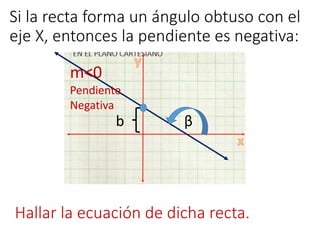
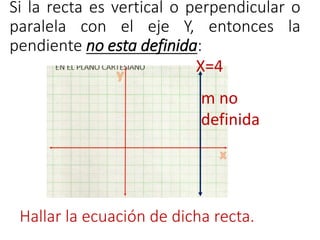
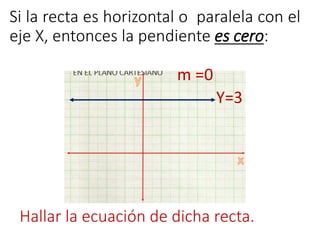
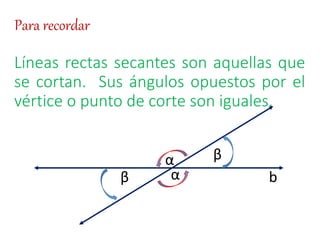
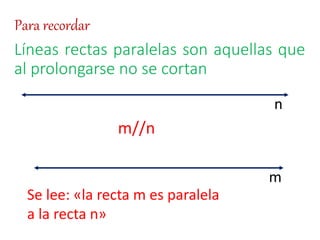
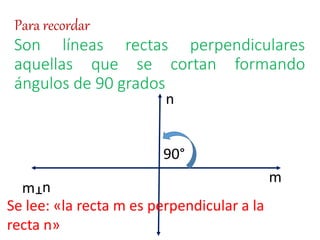
Este documento explica conceptos básicos sobre líneas rectas, incluyendo la definición de pendiente, cómo calcular la pendiente entre dos puntos, y las ecuaciones de líneas rectas. También describe cuatro casos posibles para la pendiente de una línea recta dependiendo de su ángulo de inclinación respecto al eje x, y define líneas rectas secantes, paralelas y perpendiculares.

1. LINEA RECTA.
y 
y
2 1
x x
150 
50
 m 50m
3 
1
1 2 3 4 t(h)
f(t)
250
200
150
100
50
2 1
m


2 1 y  y  y
2 1 x  x  x
Si
Son dos puntos
distintos por
donde pasa la
recta, como se
muestra en la
gráfica la
pendiente m es:
( , ) 1 1 P x y ( , ) 2 2 Q x y
( , ) 1 1 P x y
( , ) 2 2 Q x y

2. A la expresión general de la función lineal la
llamamos ecuación de la recta
Punto de corte
de la gráfica
con el eje y
y  mx  b
Pendiente de la recta
La pendiente de una recta nos indica la inclinación
de la recta respecto al eje X.

3. El signo de la pendiente de una recta
depende del ángulo de inclinación de la
recta con respecto al eje x. De acuerdo
con esto se pueden presentar cuatro
casos:

4. Si la recta forma un ángulo agudo con el
eje X, entonces la pendiente es positiva:
β
m>0
Pendiente
positiva
Hallar la ecuación de dicha recta.

5. Si la recta forma un ángulo obtuso con el
eje X, entonces la pendiente es negativa:
β
m<0
Pendiente
Negativa
b
Hallar la ecuación de dicha recta.

6. Si la recta es vertical o perpendicular o
paralela con el eje Y, entonces la
pendiente no esta definida:
X=4
m no
definida
Hallar la ecuación de dicha recta.

7. Si la recta es horizontal o paralela con el
eje X, entonces la pendiente es cero:
m =0
Y=3
Hallar la ecuación de dicha recta.

8. Para recordar
Una línea recta es una sucesión de
puntos infinitos que van en una misma
dirección y en ambos sentidos
b
Se simboliza o se identifica con una letra
minúscula

9. Para recordar
Líneas rectas secantes son aquellas que
se cortan. Sus ángulos opuestos por el
vértice o punto de corte son iguales.
b
β
β
α
α

10. Para recordar
Líneas rectas paralelas son aquellas que
al prolongarse no se cortan
n
m
m//n
Se lee: «la recta m es paralela
a la recta n»

11. Para recordar
Son líneas rectas perpendiculares
aquellas que se cortan formando
ángulos de 90 grados
m
n
90°
m
ᴛn
Se lee: «la recta m es perpendicular a la
recta n»