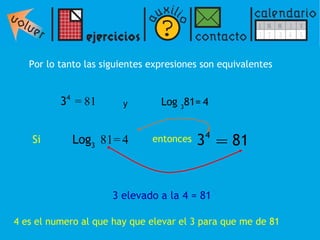
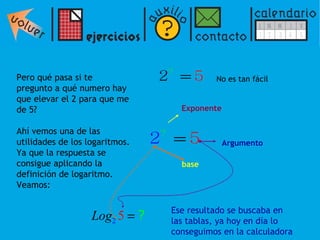
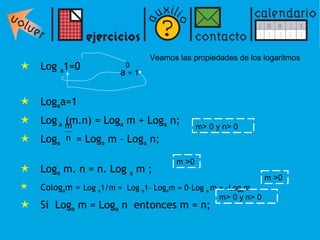
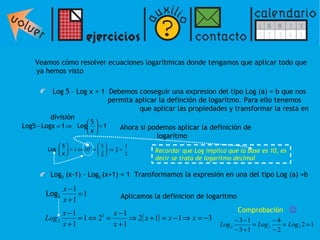
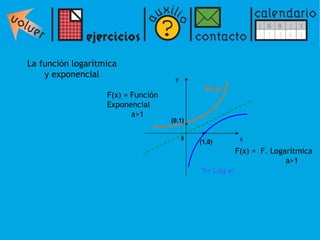
El documento presenta una introducción a los logaritmos, incluyendo su definición, propiedades y aplicaciones para resolver ecuaciones logarítmicas y exponenciales. Explica que un logaritmo representa el exponente al que debe elevarse una base para obtener un número dado. Luego describe propiedades como que el logaritmo de un producto es la suma de los logaritmos de los factores, y el logaritmo de un cociente es la diferencia de los logaritmos. Finalmente, muestra cómo usar estas propiedades para resolver ecuaciones log

1. Universidad Simón Bolívar Programa Igualdad de Oportunidades Área de Matemática LOGARITMO

2. Tema: Logaritmo Logaritmo por definición Propiedades Ecuaciones logarítmicas Ecuaciones exponenciales Función logarítmica Prerrequisitos: Propiedades de la potencia Ecuaciones lineales Operaciones con raíces Un poco de historia Sitio Web interesante para curiosear

3. OBJETIVOS DE LA UNIDAD Conocer y usar la definición de logaritmo Conocer y utilizar las propiedades de los logaritmos Resolver ecuaciones logarítmicas Resolver ecuaciones exponenciales

4. Veamos la siguiente expresión 2 3 = 8 3 es el exponente (ó potencia) a la que se debe elevar el 2 para obtener 8. El exponente se denomina Logaritmo base 2 de 8 y se escribe 3 = Log 2 8

5. Por lo tanto las siguientes expresiones son equivalentes y 3 elevado a la 4 = 81 Si entonces 4 es el numero al que hay que elevar el 3 para que me de 81

6. Pero qué pasa si te pregunto a qué numero hay que elevar el 2 para que me de 5? Ahí vemos una de las utilidades de los logaritmos. Ya que la respuesta se consigue aplicando la definición de logaritmo. Veamos: No es tan fácil base Argumento Exponente Ese resultado se buscaba en las tablas, ya hoy en día lo conseguimos en la calculadora

7. 3 4 = 81 Log 3 81= 4 Veamos en el siguiente cuadro la equivalencia entre la dos expresiones, la de potencia y la logarítmica Veamos la relación entre la expresión en forma de potencia y la logarítmica Expresión en forma de potencia Expresión logarítmica 3 3 = 27 3 = Log 3 27 5 2 = 25 2 = Log 5 25 16 1/2 = 4 ½ = Log 16 4 (3/2) 2 = 9/4 2 = Log 3/2 9/4

8. De manera general Logaritmo por definición: El logaritmo de un número respecto a cierta base es igual al exponente a que debe elevarse dicha base para encontrar el número. Logaritmo decimal: Logaritmos en base 10. Log x si no se coloca la base se supone que es en base 10 Log a 1 = 0 ⇒ a 0 = 1 El logaritmo de uno en cualquier base es cero Log a a = 1 ⇒ a 1 = a

9. Veamos varios ejemplos de logaritmo por definición Hallar e l valor de x en la expresión Log 2 x = 4 Aplicando la definición tenemos que Log 2 x = 4 ⇔ 2 4 = x; ⇒ x =16 Hallar el valor de x en la expresión log 2 64 = x Aplicando la definición tenemos que log 2 64 = x ⇔ 2 x = 64; 2 x = 2 6 ⇒ x = 6 Hallar el valor de x en la ecuación Log(2x- 4) = 1 Aplicando la definición tenemos que Log(2x- 4) = 1 ⇔ 10 1 = 2x – 4; 2x = 14 ⇒ x = 7 Hallar el valor de x en la expresión Log x 0,25 = 0,5 Aplicando la definición tenemos que Log x 0,5 = 0,25 ⇔ x 0,25 = 0,5; x ¼ = ½;

10. Propiedades de los logaritmos Sea m un numero real que escribiremos en potencias de a y en su forma logarítmica. m = a x ⇒ x = Log a m Elevando a la n la expresión m = a x nos queda (m) n = (a x ) n ⇒ m n = (a n ) x En notación logarítmica Log a m n = n. Log a m El logaritmo de una potencia es igual al exponente por el logaritmo de la base de dicha potencia Log a m n = n Log a m

11. Sean m y n dos números reales positivos cualesquiera que los escribimos en potencias de a en su forma logarítmica: m = a x ⇒ x = Log a m n = a y ⇒ y = Log a n Multiplicando ambas expresiones resulta: m  n = a x  a y ⇒ m  n =a x+y En notación logarítmica x+y = Log a (m  n) sustituyendo en esta expresión x e y por sus valores nos queda El logaritmo de un producto es igual a la suma de los logaritmos de los factores Log a (m  n) = Log a m + Log a n

12. Veamos esto a través de ejemplos: Hallar el valor del logaritmo de x en la siguiente Aplicamos logaritmo en ambos lados de la expresión Aplicamos las propiedades del logaritmo: Desarrollar la siguiente expresión Aplicamos la propiedad del producto: Log 2 2 . 3 2 a = Log 2 2 + Log 3 2 + Log a Aplicamos la propiedad de los exponentes 2log 2 + 2 Log 3 + Log a

13. Sean m y n dos números reales cualquiera que los escribimos en potencias de a en su forma logarítmica. m = a x ⇒ x = Log a m n = a y ⇒ y = Log a n Dividiendo miembro ambos miembros resulta: En notación logarítmica x – y = Log a (m/n). Sustituyendo en esta expresión x e y por sus valores nos queda El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor Log a (m/n) = Log a m - Log a n

14. Sea m un número que escribimos en potencia de a y en su forma logarítmica. m = a x ⇒ x = Log a m Sacando la raíz n a los dos miembros de la ecuación m = a x nos queda en notación logarítmica = Log a Sustituyendo en esta expresión x por su valor nos queda El logaritmo de una raíz es igual al logaritmo de la parte subradical dividido por el índice de la raíz.

15. Calcular el logaritmo en base 2 de x, sabiendo que

16. Log x, si esta comprendido entre (0,1) el logaritmo es negativo. Si esta comprendido entre (1, ∞) el logaritmo es positivo. A las sumas y restas no se les puede aplicar logaritmo Log (a  b) queda exactamente igual, ya que no existe propiedad de potenciación ni para la suma ni para la resta. Logaritmos Neperianos o naturales: Logaritmos en base e = 2,7182818285. Log e x, se denota Ln Cambio de base: Llevar Log a m a Log x Log a m =

17. Propiedades de la potencia De manera esquemática recordemos las de la potencia

18. Log a 1=0 Log a a=1 Log a (m.n) = Log a m + Log a n; Log a = Log a m – Log a n; Log a m. n = n. Log a m ; Colog a m = Log a 1/m = Log a 1- Log a m = 0–Log a m = -Log a m Si Log a m = Log a n entonces m = n; a 0 m> 0 y n> 0 = 1 Veamos las propiedades de los logaritmos m >0 m> 0 y n> 0 m >0

19. Veamos cómo resolver ecuaciones logarítmicas donde tengamos que aplicar todo que ya hemos visto Log 5 – Log x = 1 Debemos conseguir una expresion del tipo Log (a) = b que nos permita aplicar la definción de logaritmo. Para ello tenemos que aplicar las propiedades y transformar la resta en división Ahora si podemos aplicar la definición de logaritmo Log 2 (x-1) - Log 2 (x+1) = 1 Transformamos la expresión en una del tipo Log (a) =b Aplicamos la definicion de logaritmo Recordar que Log implica que la base es 10, es decir se trata de logaritmo decimal Comprobación ☺

20. Ecuaciones exponenciales: Son aquellas en las que las incógnitas forman parte de un exponente Ejemplo: Para que la igualdad sea cierta se debe cumplir que 2x -5 = 3x +2, de donde se desprende que x = -7 Calcular x en la ecuación Podemos transformarla en obtenemos que x = 7. En general Ejemplo:

21. La función logarítmica y exponencial F(x) = Función Exponencial a>1 F(x) = F. Logarítmica a>1 y x (1,0) (0,1) 0 Y= a x Y= Log a x

22. Propiedades de la función logarítmica Dom F(x) = R + Rgo F(x) = R F(x) es creciente Cero de la función es 1, ya que (log a 1= 0) La gráfica de la función logarítmica es simétrica a la gráfica de la exponencial respecto a la bisectriz del primer cuadrante Si consideras que estas listo aquí tienes una prueba de auto evaluación que te dará una idea de tu nivel de preparación